2023年浙江省宁波市九年级强基竞赛联考数学试题(含答案)
文档属性
| 名称 | 2023年浙江省宁波市九年级强基竞赛联考数学试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 09:00:24 | ||
图片预览


文档简介
九年级数学竞赛联考试卷
一、选择题(第1-8题各6分,第9~10题各8分,共64分)
1.下列计算正确的是( )
A. B.
C. D.
2.一个盒子里有完全相同的三个小球,球上分别标上数字1、2、4.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程有两个不相等实数根的概率是( )
A. B. C. D.
3.若,,则b、、、ab中最大的一个数是( )
A.b B. C. D.ab
4.若关于x的不等式组共有2个整数解,则m的取值范围是( )
A. B. C. D.
5.如图所示的是反比例函数和一次函数的图象,则下列结论正确的是( )
A.反比例函数的解析式是 B.一次函数的解析式为
C.当时,最大值为1 D.若,则
6.二次函数的图象与x轴的两个交点为,,且点是图象上一点,那么下列判断正确的是( )
A.当时, B.当时,
C.当时, D.当时,
7.商店为了对某种商品促销,将定价为30元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折,现有270元,最多可以购买该商品的件数是( )
A.9件 B.10件 C.11件 D.12件
8.已知:a、b是正数,且,则的最小值是( )
A. B. C. D.
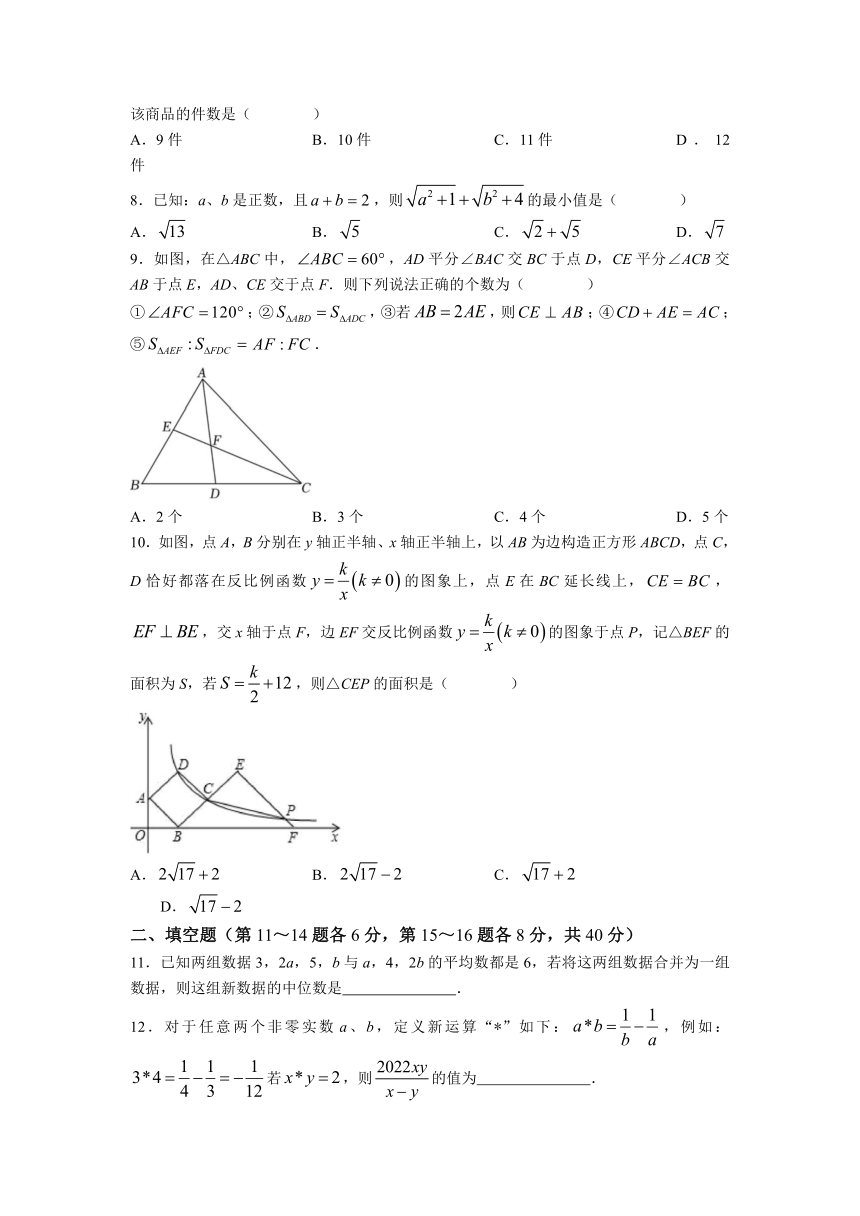
9.如图,在△ABC中,,AD平分∠BAC交BC于点D,CE平分∠ACB交AB于点E,AD、CE交于点F.则下列说法正确的个数为( )
①;②,③若,则;④;⑤.
A.2个 B.3个 C.4个 D.5个
10.如图,点A,B分别在y轴正半轴、x轴正半轴上,以AB为边构造正方形ABCD,点C,D恰好都落在反比例函数的图象上,点E在BC延长线上,,,交x轴于点F,边EF交反比例函数的图象于点P,记△BEF的面积为S,若,则△CEP的面积是( )
A. B. C. D.
二、填空题(第11~14题各6分,第15~16题各8分,共40分)
11.已知两组数据3,2a,5,b与a,4,2b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数是 .
12.对于任意两个非零实数a、b,定义新运算“*”如下:,例如:若,则的值为 .
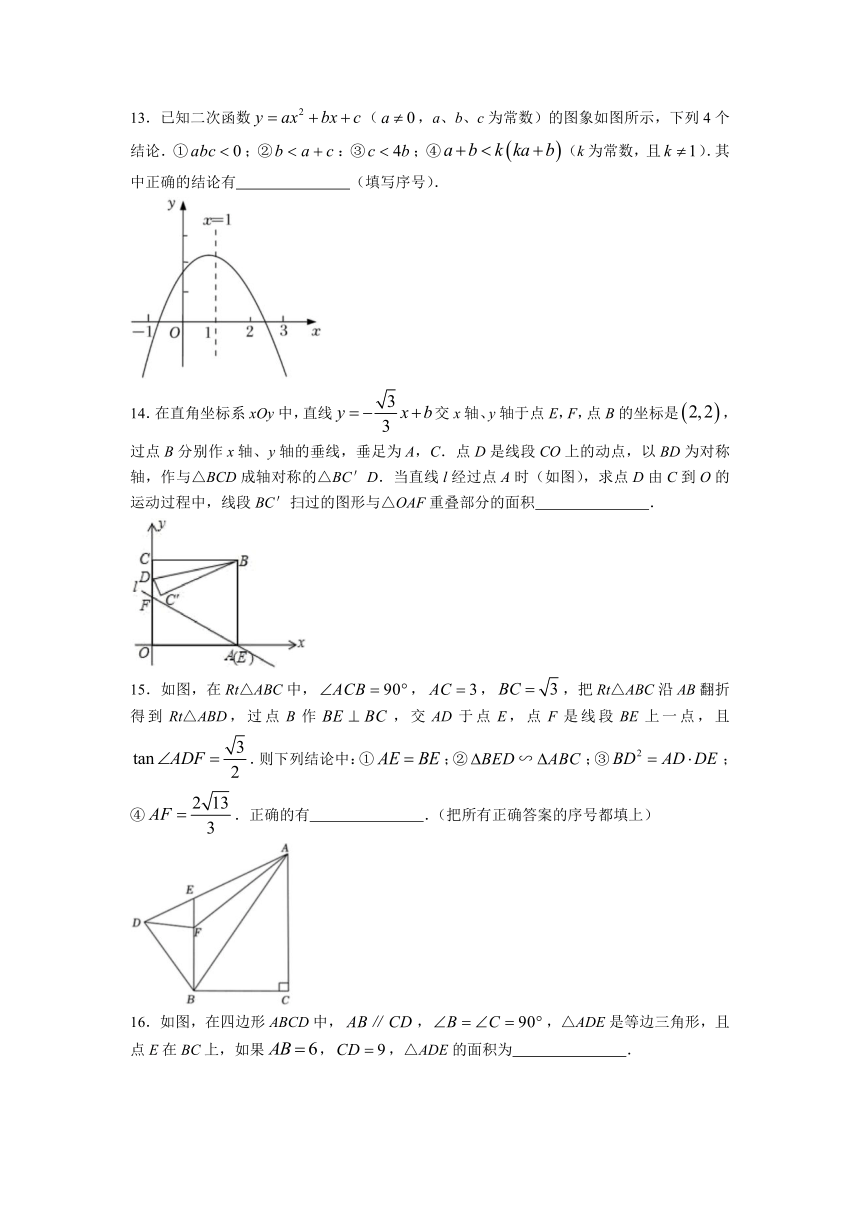
13.已知二次函数(,a、b、c为常数)的图象如图所示,下列4个结论.①;②:③;④(k为常数,且).其中正确的结论有 (填写序号).
14.在直角坐标系xOy中,直线交x轴、y轴于点E,F,点B的坐标是,过点B分别作x轴、y轴的垂线,垂足为A,C.点D是线段CO上的动点,以BD为对称轴,作与△BCD成轴对称的△BC'D.当直线l经过点A时(如图),求点D由C到O的运动过程中,线段BC'扫过的图形与△OAF重叠部分的面积 .
15.如图,在Rt△ABC中,,,,把Rt△ABC沿AB翻折得到Rt△ABD,过点B作,交AD于点E,点F是线段BE上一点,且.则下列结论中:①;②;③;④.正确的有 .(把所有正确答案的序号都填上)
16.如图,在四边形ABCD中,,,△ADE是等边三角形,且点E在BC上,如果,,△ADE的面积为 .
三、解答题(第17~18题各12分,第19题14分,第20题18分,第21~22题各20分,共96分)
17.一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图象分别表示货车、轿车离甲地距离y(km)与轿车行驶时间x(h)的关系.
(1)求轿车在返回甲地过程中的速度;
(2)当轿车从乙地返回甲地的途中与货车相遇时,求相遇处离甲地的距离.
18.已知抛物线.
(1)若此抛物线与x轴只有一个公共点且过点.
①求此抛物线的解析式;
②直线与该抛物线交于点和点B.若,求x的取值范围.
(2)若,将此抛物线向上平移c个单位()得到新抛物线,当时,;当时,,试比较ac与1的大小,并说明理由,
19.对于任意一个四位数,我们可以记为,即.若规定:对四位正整数进行F运算,得到整数,例如,; .
(1)计算:;
(2)当时,证明:的结果一定是4的倍数;
(3)求出满足的所有四位数.
20.如图,在△ABC外分别以AB,AC为边作正方形ABDE和正方形ACFG,连接EG,AM是△ABC中BC边上的中线,延长MA交EG于点H,求证:
(1);
(2);
(3).
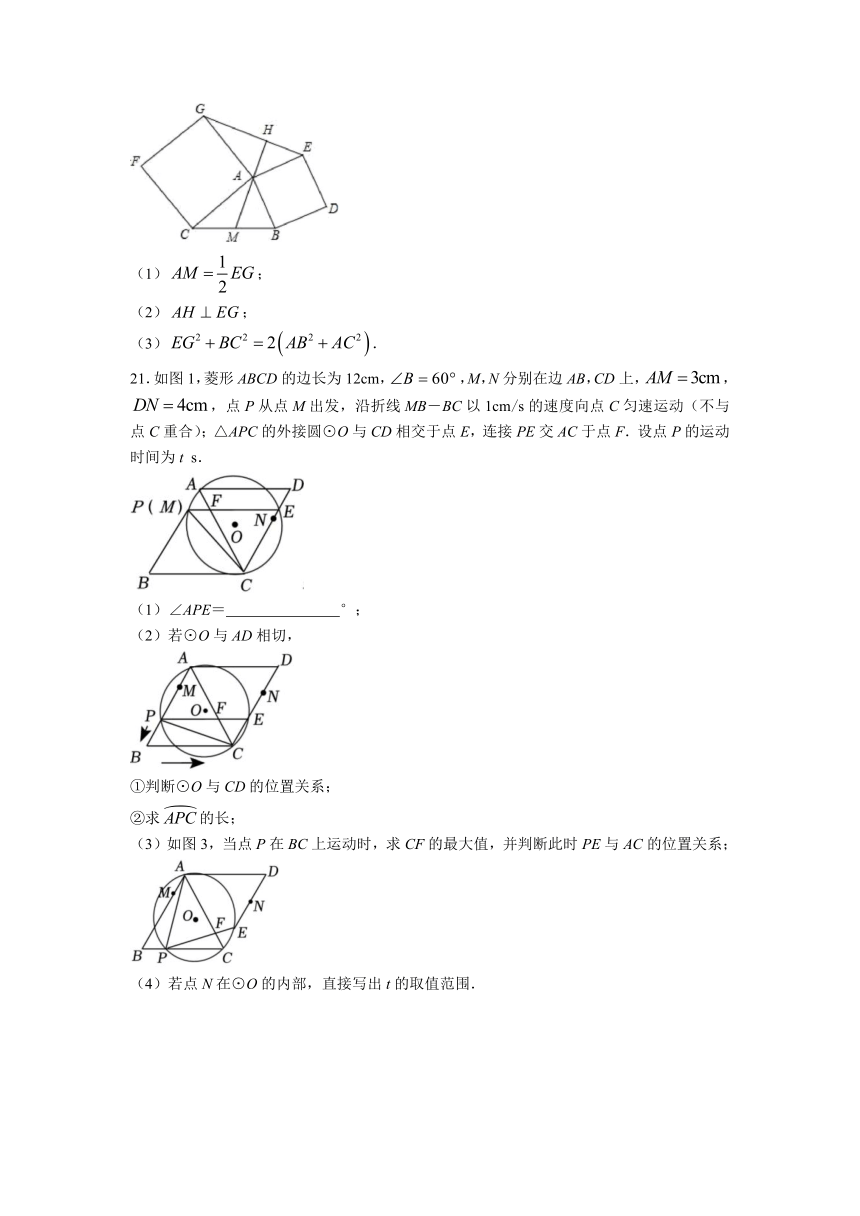
21.如图1,菱形ABCD的边长为12cm,,M,N分别在边AB,CD上,,,点P从点M出发,沿折线MB-BC以1cm/s的速度向点C匀速运动(不与点C重合);△APC的外接圆⊙O与CD相交于点E,连接PE交AC于点F.设点P的运动时间为t s.
(1)∠APE= °;
(2)若⊙O与AD相切,
①判断⊙O与CD的位置关系;
②求的长;
(3)如图3,当点P在BC上运动时,求CF的最大值,并判断此时PE与AC的位置关系;
(4)若点N在⊙O的内部,直接写出t的取值范围.
22.【证明体验】
如图1,四边形ABCD和四边形AEFG都是菱形,,点G,点E分别在边AD,AB上,点F在菱形ABCD内部,将菱形AEFG绕点A旋转一定的角度α,点E,F始终在菱形ABCD的内部.
(1)图2,求证:.
【思考探究】
(2)如图3,点P,Q分别在AB,AD延长线上,连接AF并延长与∠QDC的平分线交于点H,连接AE并延长与∠PBC的平分线交于K.连接DH,HK,CH,CK,
①求证:.
②若,,则线段BK的长度为 ,线段HK的长为 .
③菱形AEFG绕点A旋转α度(),,△KBC是等腰三角形,线段HK的长为 .
九年级数学竞赛联考试卷
参考答案与试题解析
一、选择题(第1~8题各6分,第9~10题各8分,共64分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C B D D B A C B
二、填空题(第11~14题各6分,第15~16题各8分,共40分)
11.5
12.1011
13.①③
14.
15.①②③④
16.
三、解答题(第17~18题各12分,第19题14分,第20题18分,第21~22题各20分,共96分)
17.解:
(1)根据图象可得当小时时,离甲地的距离是120千米,当小时时,离甲地的距离是0千米,
∴轿车在返回甲地过程中的速度为:(千米/小时),
答:轿车在返回甲地过程中的速度为80千米/小时;
(2)设货车离甲地的距离y(千米)与轿车行驶时间x(小时)的函数解析式是,则,
解得:,
则函数解析式是;
设轿车在返回甲地过程中离甲地的距离y(千米)与轿车行驶时间x(小时)的解析式是,
则,
解得
则函数解析式是.
根据题意得:,
解得:,
则轿车从乙地返回甲地的途中与货车相遇时,相遇处到甲地的距离是(千米).
答:当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离是千米.
18.解:
(1)①∵抛物线与x轴只有一个公共点,
∴,
∴,
又∵抛物线过点.
∴,
∴抛物线的解析式;
②当时,,
∴,
∴,
∴,
∴,
联立方程组,
解得或,
∴,,
∴当时,或;
(2),理由:
由题知,将此抛物线向上平移c个单位(),
其解析式为,且过点,
∴,
∴,
∴,
且当时,,
对称轴:,抛物线开口向上,画草图如右所示.
由题知,当时,.
∴,
∴,
∴,
∴;
19.解:
(1);
(2)∴,
∵,
原式,
∵,且e是整数,
∴是4的倍数.
所以,当时,的结果一定是4的倍数.
(3)∵,
∴,即.
∵,
∴.
∴,且x为整数.
∴或或或.
所以,满足条件的四位数有3209,3218,3225,3230.
20.
(1)证明:延长AM到点N,使,连接BN,
∵AM是△ABC中BC边上的中线,
∴CM=BM,
在△MBN和△MCA中
∴,
∴∠BNM=∠CAM,NB=AC,
∴BN∥AC,NB=AG,
∴∠NBA+∠BAC=180°,
∵∠GAE+∠BAC=360°-90°-90°=180°,
∴∠NBA=∠GAE
在△NBA和△GAE中
∴,
∴AN=EG,
∴;
(2)证明:
由(1)得∠BAN=∠AEG,
∵∠HAE+∠BAN=180°-90°=90°,
∴∠HAE+∠AEH=90°,
∴
即;
(3)证明:连接CE、BG,
易证
∴,
∴,
∴.
21.解:
(1)∵四边形ABCD为菱形,,
∴∠D=∠B=60°,,
∴△ACD为等边三角形,
∴,
∴∠APE=∠ACE=60°,
故答案为:60;
(2)如图,当点P运动到点B时,⊙O与AD相切,
①∵四边形ABCD为菱形,
∴,
∵⊙O与AD相切,
∴⊙O与CD相切;
②连接OD,
由(1)可知,,
∵AD、CD分别与⊙O相切,
∴,
∴,
∴弧APC的长;
(3)由图可知:,
∵,,
∴△ABC为等边三角形,
则,,
∴要使CF取得最大值,
则AF应该取最小值,
当时,AF最小,此时CF取得最大值,
∵点O为△APC外接圆圆心,
∴,
∵,
∴,
综上:CF的最大值为3cm,此时;
(4)①当点P在AB上时,
∵四边形APCE为圆的内接四边形,
∴∠APC+∠AEC=180°,
∵∠AED+∠AEC=180°,
∴∠APC=∠AED,
在△APC和△DEA中,AC=AD,∠PAC=∠D,∠APC=∠AED,
∴,
∴,
当点E与点N重合时,DE=AP=DN=4,
∵MP=4-3=1cm,
∴,
当时,点N在圆内部;
②当点P在BC上运动时,
∵∠AEP=∠ACP=60°,
∴△APE为等边三角形,
∴,∠PAE=60°,
∵,
∴∠BAP=∠CAE,
在△BAP和△CAE中,AB=AC,∠BAP=∠CAE,AP=AE,
∴
∴,
当点E与点N重合时,CE=CN=BP=12-4=8cm,
此时,
当点P到达点C时,,
当时,点N在圆内部;
综上:当时或时,点N在圆内部.
22.
(1)证明:如图2中,
∵四边形ABCD和四边形AEFG都是菱形,,
∴,AC=AE,∠GAD=∠EAB,
在△GAD和△EAB中,
,
∴;
(2)①证明:如图3-1中,
∵四边形ABCD是菱形,
∴AB∥CD,AD∥BC,
∴∠CBP=∠DAB=60°,∠CDQ=∠DAB=60°,
∵DH,BK分别平分∠QDC,∠CBP,
∴∠QDH=∠KBP=30°,
∴∠ADH=∠ABK=150°,
∵∠FAE=∠QDH=30°,
∴∠DAH+∠AHD=∠BAK+∠DAH=30°,
∴∠AHD=∠BAK,
∴;
②解:如图3-2中,连接DB,过点H作HM⊥BK于点M.
∵,
∴,
∴,
∵∠BDH=∠DBM=∠BMH=90°,
∴四边形DBMH是矩形,
∴,,
∴KM=BK-BM=8-5=3,
∴.
故答案为:8,7;
③解:如图4-1中,当KB=KC时,连接BD,过点K作于点J,
∵,,
∴,,
∵AB=BC=m,∠CBK=∠KCB=30°,
∴,
∴,
∵四边形BDJK是矩形,
∴,DB=KJ=m,
∴,
∴
如图4-2中,当BC=BK时,四边形BDHK是正方形kH=m.
如图4-3中,时,D,C,K共线,过点H作HN⊥BK于点N.
∵,,
∴,
∴,
∵四边形BDHN是矩形,
∴,,
∴,
∴,
综上所述,满足条件的HK的值为m或.
故答案为:m或.
一、选择题(第1-8题各6分,第9~10题各8分,共64分)
1.下列计算正确的是( )
A. B.
C. D.
2.一个盒子里有完全相同的三个小球,球上分别标上数字1、2、4.随机摸出一个小球(不放回)其数字记为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程有两个不相等实数根的概率是( )
A. B. C. D.
3.若,,则b、、、ab中最大的一个数是( )
A.b B. C. D.ab
4.若关于x的不等式组共有2个整数解,则m的取值范围是( )
A. B. C. D.
5.如图所示的是反比例函数和一次函数的图象,则下列结论正确的是( )
A.反比例函数的解析式是 B.一次函数的解析式为
C.当时,最大值为1 D.若,则
6.二次函数的图象与x轴的两个交点为,,且点是图象上一点,那么下列判断正确的是( )
A.当时, B.当时,
C.当时, D.当时,
7.商店为了对某种商品促销,将定价为30元的商品,以下列方式优惠销售:若购买不超过5件,按原价付款;若一次性购买5件以上,超过部分打八折,现有270元,最多可以购买该商品的件数是( )
A.9件 B.10件 C.11件 D.12件
8.已知:a、b是正数,且,则的最小值是( )
A. B. C. D.
9.如图,在△ABC中,,AD平分∠BAC交BC于点D,CE平分∠ACB交AB于点E,AD、CE交于点F.则下列说法正确的个数为( )
①;②,③若,则;④;⑤.
A.2个 B.3个 C.4个 D.5个
10.如图,点A,B分别在y轴正半轴、x轴正半轴上,以AB为边构造正方形ABCD,点C,D恰好都落在反比例函数的图象上,点E在BC延长线上,,,交x轴于点F,边EF交反比例函数的图象于点P,记△BEF的面积为S,若,则△CEP的面积是( )
A. B. C. D.
二、填空题(第11~14题各6分,第15~16题各8分,共40分)
11.已知两组数据3,2a,5,b与a,4,2b的平均数都是6,若将这两组数据合并为一组数据,则这组新数据的中位数是 .
12.对于任意两个非零实数a、b,定义新运算“*”如下:,例如:若,则的值为 .
13.已知二次函数(,a、b、c为常数)的图象如图所示,下列4个结论.①;②:③;④(k为常数,且).其中正确的结论有 (填写序号).
14.在直角坐标系xOy中,直线交x轴、y轴于点E,F,点B的坐标是,过点B分别作x轴、y轴的垂线,垂足为A,C.点D是线段CO上的动点,以BD为对称轴,作与△BCD成轴对称的△BC'D.当直线l经过点A时(如图),求点D由C到O的运动过程中,线段BC'扫过的图形与△OAF重叠部分的面积 .
15.如图,在Rt△ABC中,,,,把Rt△ABC沿AB翻折得到Rt△ABD,过点B作,交AD于点E,点F是线段BE上一点,且.则下列结论中:①;②;③;④.正确的有 .(把所有正确答案的序号都填上)
16.如图,在四边形ABCD中,,,△ADE是等边三角形,且点E在BC上,如果,,△ADE的面积为 .
三、解答题(第17~18题各12分,第19题14分,第20题18分,第21~22题各20分,共96分)
17.一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图象分别表示货车、轿车离甲地距离y(km)与轿车行驶时间x(h)的关系.
(1)求轿车在返回甲地过程中的速度;
(2)当轿车从乙地返回甲地的途中与货车相遇时,求相遇处离甲地的距离.
18.已知抛物线.
(1)若此抛物线与x轴只有一个公共点且过点.
①求此抛物线的解析式;
②直线与该抛物线交于点和点B.若,求x的取值范围.
(2)若,将此抛物线向上平移c个单位()得到新抛物线,当时,;当时,,试比较ac与1的大小,并说明理由,
19.对于任意一个四位数,我们可以记为,即.若规定:对四位正整数进行F运算,得到整数,例如,; .
(1)计算:;
(2)当时,证明:的结果一定是4的倍数;
(3)求出满足的所有四位数.
20.如图,在△ABC外分别以AB,AC为边作正方形ABDE和正方形ACFG,连接EG,AM是△ABC中BC边上的中线,延长MA交EG于点H,求证:
(1);
(2);
(3).
21.如图1,菱形ABCD的边长为12cm,,M,N分别在边AB,CD上,,,点P从点M出发,沿折线MB-BC以1cm/s的速度向点C匀速运动(不与点C重合);△APC的外接圆⊙O与CD相交于点E,连接PE交AC于点F.设点P的运动时间为t s.
(1)∠APE= °;
(2)若⊙O与AD相切,
①判断⊙O与CD的位置关系;
②求的长;
(3)如图3,当点P在BC上运动时,求CF的最大值,并判断此时PE与AC的位置关系;
(4)若点N在⊙O的内部,直接写出t的取值范围.
22.【证明体验】
如图1,四边形ABCD和四边形AEFG都是菱形,,点G,点E分别在边AD,AB上,点F在菱形ABCD内部,将菱形AEFG绕点A旋转一定的角度α,点E,F始终在菱形ABCD的内部.
(1)图2,求证:.
【思考探究】
(2)如图3,点P,Q分别在AB,AD延长线上,连接AF并延长与∠QDC的平分线交于点H,连接AE并延长与∠PBC的平分线交于K.连接DH,HK,CH,CK,
①求证:.
②若,,则线段BK的长度为 ,线段HK的长为 .
③菱形AEFG绕点A旋转α度(),,△KBC是等腰三角形,线段HK的长为 .
九年级数学竞赛联考试卷
参考答案与试题解析
一、选择题(第1~8题各6分,第9~10题各8分,共64分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A C B D D B A C B
二、填空题(第11~14题各6分,第15~16题各8分,共40分)
11.5
12.1011
13.①③
14.
15.①②③④
16.
三、解答题(第17~18题各12分,第19题14分,第20题18分,第21~22题各20分,共96分)
17.解:
(1)根据图象可得当小时时,离甲地的距离是120千米,当小时时,离甲地的距离是0千米,
∴轿车在返回甲地过程中的速度为:(千米/小时),
答:轿车在返回甲地过程中的速度为80千米/小时;
(2)设货车离甲地的距离y(千米)与轿车行驶时间x(小时)的函数解析式是,则,
解得:,
则函数解析式是;
设轿车在返回甲地过程中离甲地的距离y(千米)与轿车行驶时间x(小时)的解析式是,
则,
解得
则函数解析式是.
根据题意得:,
解得:,
则轿车从乙地返回甲地的途中与货车相遇时,相遇处到甲地的距离是(千米).
答:当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离是千米.
18.解:
(1)①∵抛物线与x轴只有一个公共点,
∴,
∴,
又∵抛物线过点.
∴,
∴抛物线的解析式;
②当时,,
∴,
∴,
∴,
∴,
联立方程组,
解得或,
∴,,
∴当时,或;
(2),理由:
由题知,将此抛物线向上平移c个单位(),
其解析式为,且过点,
∴,
∴,
∴,
且当时,,
对称轴:,抛物线开口向上,画草图如右所示.
由题知,当时,.
∴,
∴,
∴,
∴;
19.解:
(1);
(2)∴,
∵,
原式,
∵,且e是整数,
∴是4的倍数.
所以,当时,的结果一定是4的倍数.
(3)∵,
∴,即.
∵,
∴.
∴,且x为整数.
∴或或或.
所以,满足条件的四位数有3209,3218,3225,3230.
20.
(1)证明:延长AM到点N,使,连接BN,
∵AM是△ABC中BC边上的中线,
∴CM=BM,
在△MBN和△MCA中
∴,
∴∠BNM=∠CAM,NB=AC,
∴BN∥AC,NB=AG,
∴∠NBA+∠BAC=180°,
∵∠GAE+∠BAC=360°-90°-90°=180°,
∴∠NBA=∠GAE
在△NBA和△GAE中
∴,
∴AN=EG,
∴;
(2)证明:
由(1)得∠BAN=∠AEG,
∵∠HAE+∠BAN=180°-90°=90°,
∴∠HAE+∠AEH=90°,
∴
即;
(3)证明:连接CE、BG,
易证
∴,
∴,
∴.
21.解:
(1)∵四边形ABCD为菱形,,
∴∠D=∠B=60°,,
∴△ACD为等边三角形,
∴,
∴∠APE=∠ACE=60°,
故答案为:60;
(2)如图,当点P运动到点B时,⊙O与AD相切,
①∵四边形ABCD为菱形,
∴,
∵⊙O与AD相切,
∴⊙O与CD相切;
②连接OD,
由(1)可知,,
∵AD、CD分别与⊙O相切,
∴,
∴,
∴弧APC的长;
(3)由图可知:,
∵,,
∴△ABC为等边三角形,
则,,
∴要使CF取得最大值,
则AF应该取最小值,
当时,AF最小,此时CF取得最大值,
∵点O为△APC外接圆圆心,
∴,
∵,
∴,
综上:CF的最大值为3cm,此时;
(4)①当点P在AB上时,
∵四边形APCE为圆的内接四边形,
∴∠APC+∠AEC=180°,
∵∠AED+∠AEC=180°,
∴∠APC=∠AED,
在△APC和△DEA中,AC=AD,∠PAC=∠D,∠APC=∠AED,
∴,
∴,
当点E与点N重合时,DE=AP=DN=4,
∵MP=4-3=1cm,
∴,
当时,点N在圆内部;
②当点P在BC上运动时,
∵∠AEP=∠ACP=60°,
∴△APE为等边三角形,
∴,∠PAE=60°,
∵,
∴∠BAP=∠CAE,
在△BAP和△CAE中,AB=AC,∠BAP=∠CAE,AP=AE,
∴
∴,
当点E与点N重合时,CE=CN=BP=12-4=8cm,
此时,
当点P到达点C时,,
当时,点N在圆内部;
综上:当时或时,点N在圆内部.
22.
(1)证明:如图2中,
∵四边形ABCD和四边形AEFG都是菱形,,
∴,AC=AE,∠GAD=∠EAB,
在△GAD和△EAB中,
,
∴;
(2)①证明:如图3-1中,
∵四边形ABCD是菱形,
∴AB∥CD,AD∥BC,
∴∠CBP=∠DAB=60°,∠CDQ=∠DAB=60°,
∵DH,BK分别平分∠QDC,∠CBP,
∴∠QDH=∠KBP=30°,
∴∠ADH=∠ABK=150°,
∵∠FAE=∠QDH=30°,
∴∠DAH+∠AHD=∠BAK+∠DAH=30°,
∴∠AHD=∠BAK,
∴;
②解:如图3-2中,连接DB,过点H作HM⊥BK于点M.
∵,
∴,
∴,
∵∠BDH=∠DBM=∠BMH=90°,
∴四边形DBMH是矩形,
∴,,
∴KM=BK-BM=8-5=3,
∴.
故答案为:8,7;
③解:如图4-1中,当KB=KC时,连接BD,过点K作于点J,
∵,,
∴,,
∵AB=BC=m,∠CBK=∠KCB=30°,
∴,
∴,
∵四边形BDJK是矩形,
∴,DB=KJ=m,
∴,
∴
如图4-2中,当BC=BK时,四边形BDHK是正方形kH=m.
如图4-3中,时,D,C,K共线,过点H作HN⊥BK于点N.
∵,,
∴,
∴,
∵四边形BDHN是矩形,
∴,,
∴,
∴,
综上所述,满足条件的HK的值为m或.
故答案为:m或.
同课章节目录
