北师大版九年级下册3.6 直线和圆的位置关系巩固练习(无答案)
文档属性
| 名称 | 北师大版九年级下册3.6 直线和圆的位置关系巩固练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 297.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 10:58:08 | ||
图片预览

文档简介
3.6 直线和圆的位置关系(巩固练习)-北师大九年级下册
一.选择题
1.已知⊙O的半径等于5,圆心O到直线l的距离为4,那么直线l与⊙O的公共点的个数是( )
A.0 B.1 C.2 D.无法确定
2.如图,在△ABC中,点D为△ABC的内心,CD=4,BD=6.则△DBC的面积是( )
A.6 B.5 C.4 D.3
3.如图,在△ABC中,∠ACB=90°,三个切点分别为点D,E,F.若BF=2,则△ABC的周长是( )
A.9 B. C.10 D.12
4.如图,AB是⊙O的直径,C,D是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若OE=4( )
A.2 B. C.2 D.
.如图,AB与⊙O相切于点F,AC与⊙O交于C、D两点,BE⊥CD于点E,且BE经过圆心,若OD=5,CD=8( )
A.5+3 B.5 C.2 D.4
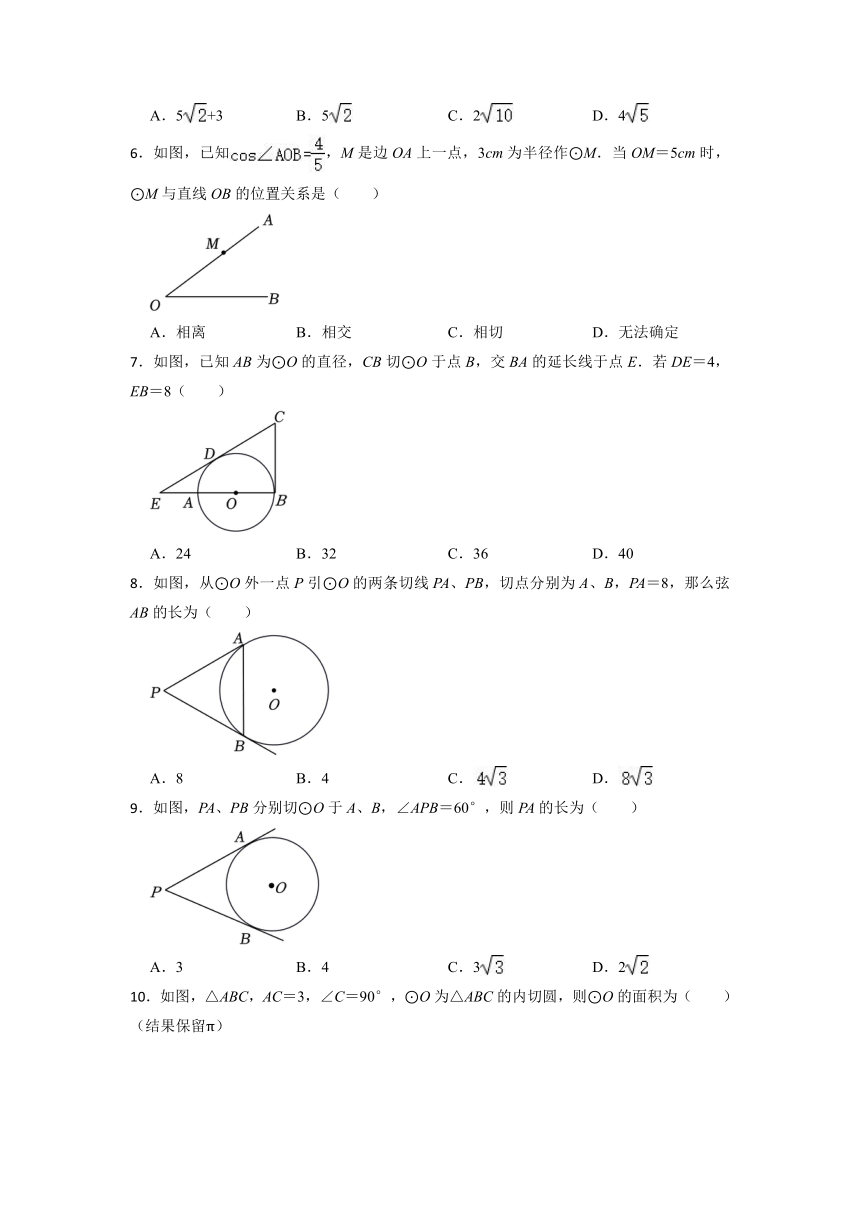
.如图,已知,M是边OA上一点,3cm为半径作⊙M.当OM=5cm时,⊙M与直线OB的位置关系是( )
A.相离 B.相交 C.相切 D.无法确定
.如图,已知AB为⊙O的直径,CB切⊙O于点B,交BA的延长线于点E.若DE=4,EB=8( )
A.24 B.32 C.36 D.40
.如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别为A、B,PA=8,那么弦AB的长为( )
A.8 B.4 C. D.
.如图,PA、PB分别切⊙O于A、B,∠APB=60°,则PA的长为( )
A.3 B.4 C.3 D.2
.如图,△ABC,AC=3,∠C=90°,⊙O为△ABC的内切圆,则⊙O的面积为( )(结果保留π)
A.π B.2π C.3π D.4π
二.填空题
.如图,AB、AC与⊙O相切于点 B、C,∠A=50°,则∠BPC的度数为 °.
.如图,PA、PB分别与⊙O相切于点A,B,连结PO并延长与⊙O交于点C、D,PA=8,则sin∠ADB的值为 .
.在△ACB中,AB=10,AC=8,点O是△ACB的内心,过O作OD⊥AB于D点.
(1)∠C= ;
(2)AD= .
.如图,等边△ABC内切圆的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称.若等边△ABC的边长为6 .
.如图,已知⊙O是△ABC的内切圆,切点分别为D,E,F,CD=2,BF=3,则内切圆的半径r为 .
三.解答题
.如图,AB是⊙O的直径,F为⊙O上一点
(1)求证:CD是⊙O的切线.
(2)若DC=3,AD=9,求⊙O半径.
.如图,点O是矩形ABCD中AB边上的一点,以O为圆心,⊙O交CD边于点E,且恰好过点D,过点E作EF∥BD,若∠BOD=120°.
(1)求∠CEF的度数;
(2)求证:EF是⊙O的切线.
.数学课上,王老师画好图后并出示如下内容:“已知AB为⊙O的直径,⊙O过AC的中点D.DE为⊙O的切线.
(1)求证DE⊥BC;
(2)王老师说:如果添加条件“DE=1,tanC=,则能求出⊙O的直径.请你写出求解过程.
.如图,已知平行四边形OABC的三个顶点A,B,C在以O为圆心的半圆上,分别交AB,AO的延长线于点D,E,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由.
(2)①求证:BC=CF;
②若半圆O的半径为4,求阴影部分的面积.
.如图,直线AB,BC,且AB∥CD,OB=5cm
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
一.选择题
1.已知⊙O的半径等于5,圆心O到直线l的距离为4,那么直线l与⊙O的公共点的个数是( )
A.0 B.1 C.2 D.无法确定
2.如图,在△ABC中,点D为△ABC的内心,CD=4,BD=6.则△DBC的面积是( )
A.6 B.5 C.4 D.3
3.如图,在△ABC中,∠ACB=90°,三个切点分别为点D,E,F.若BF=2,则△ABC的周长是( )
A.9 B. C.10 D.12
4.如图,AB是⊙O的直径,C,D是⊙O上的点,过点C作⊙O的切线交AB的延长线于点E,若OE=4( )
A.2 B. C.2 D.
.如图,AB与⊙O相切于点F,AC与⊙O交于C、D两点,BE⊥CD于点E,且BE经过圆心,若OD=5,CD=8( )
A.5+3 B.5 C.2 D.4
.如图,已知,M是边OA上一点,3cm为半径作⊙M.当OM=5cm时,⊙M与直线OB的位置关系是( )
A.相离 B.相交 C.相切 D.无法确定
.如图,已知AB为⊙O的直径,CB切⊙O于点B,交BA的延长线于点E.若DE=4,EB=8( )
A.24 B.32 C.36 D.40
.如图,从⊙O外一点P引⊙O的两条切线PA、PB,切点分别为A、B,PA=8,那么弦AB的长为( )
A.8 B.4 C. D.
.如图,PA、PB分别切⊙O于A、B,∠APB=60°,则PA的长为( )
A.3 B.4 C.3 D.2
.如图,△ABC,AC=3,∠C=90°,⊙O为△ABC的内切圆,则⊙O的面积为( )(结果保留π)
A.π B.2π C.3π D.4π
二.填空题
.如图,AB、AC与⊙O相切于点 B、C,∠A=50°,则∠BPC的度数为 °.
.如图,PA、PB分别与⊙O相切于点A,B,连结PO并延长与⊙O交于点C、D,PA=8,则sin∠ADB的值为 .
.在△ACB中,AB=10,AC=8,点O是△ACB的内心,过O作OD⊥AB于D点.
(1)∠C= ;
(2)AD= .
.如图,等边△ABC内切圆的图形来自我国古代的太极图,等边三角形内切圆中的黑色部分和白色部分关于等边△ABC的内心成中心对称.若等边△ABC的边长为6 .
.如图,已知⊙O是△ABC的内切圆,切点分别为D,E,F,CD=2,BF=3,则内切圆的半径r为 .
三.解答题
.如图,AB是⊙O的直径,F为⊙O上一点
(1)求证:CD是⊙O的切线.
(2)若DC=3,AD=9,求⊙O半径.
.如图,点O是矩形ABCD中AB边上的一点,以O为圆心,⊙O交CD边于点E,且恰好过点D,过点E作EF∥BD,若∠BOD=120°.
(1)求∠CEF的度数;
(2)求证:EF是⊙O的切线.
.数学课上,王老师画好图后并出示如下内容:“已知AB为⊙O的直径,⊙O过AC的中点D.DE为⊙O的切线.
(1)求证DE⊥BC;
(2)王老师说:如果添加条件“DE=1,tanC=,则能求出⊙O的直径.请你写出求解过程.
.如图,已知平行四边形OABC的三个顶点A,B,C在以O为圆心的半圆上,分别交AB,AO的延长线于点D,E,连接CF.
(1)判断直线DE与半圆O的位置关系,并说明理由.
(2)①求证:BC=CF;
②若半圆O的半径为4,求阴影部分的面积.
.如图,直线AB,BC,且AB∥CD,OB=5cm
(1)∠BOC的度数;
(2)BE+CG的长;
(3)⊙O的半径.
