人教版八年级下册18.2.1 矩形 课后练习(含解析)
文档属性
| 名称 | 人教版八年级下册18.2.1 矩形 课后练习(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 618.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 11:42:36 | ||
图片预览



文档简介
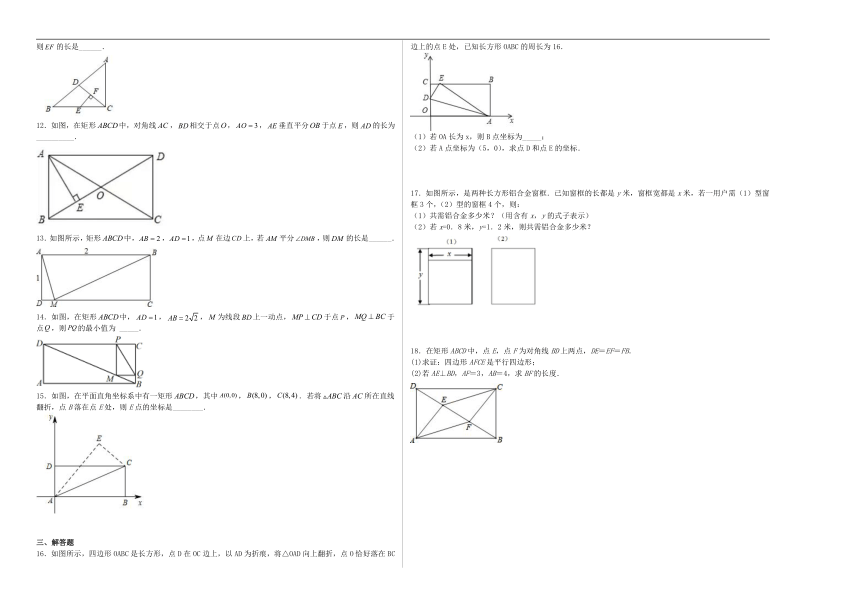
18.2.1 矩形 课后练习
一、单选题
1.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为2.8km,则M,C两点间的距离为( )
A.1.5km B.2.8km C.1.4km D.1.9km
2.如图:一张宽度相等的纸条折叠后,若∠ABC=120°,则∠1的度数是( )
A.80° B.70° C.60° D.50°
3.如图,矩形ABCD的对角线AC,BD相交于点O,AD=3,∠AOD=60°,则AB的长为( )
A.3 B.2 C.3 D.6
4.要使平行四边形成为矩形,需要添加的条件是( )
A. B. C. D.
5.在中,,分别以A点,B点为圆心以大于为半径画弧,两弧交于E,F,连接交于点D,连接,以C为圆心,长为半径作弧,交于G点,则( )
A. B.1:2 C. D.
6.如图在矩形中,,,将沿对角线翻折,点落在点处,交于点,则的面积为( )
A. B. C.21 D.24
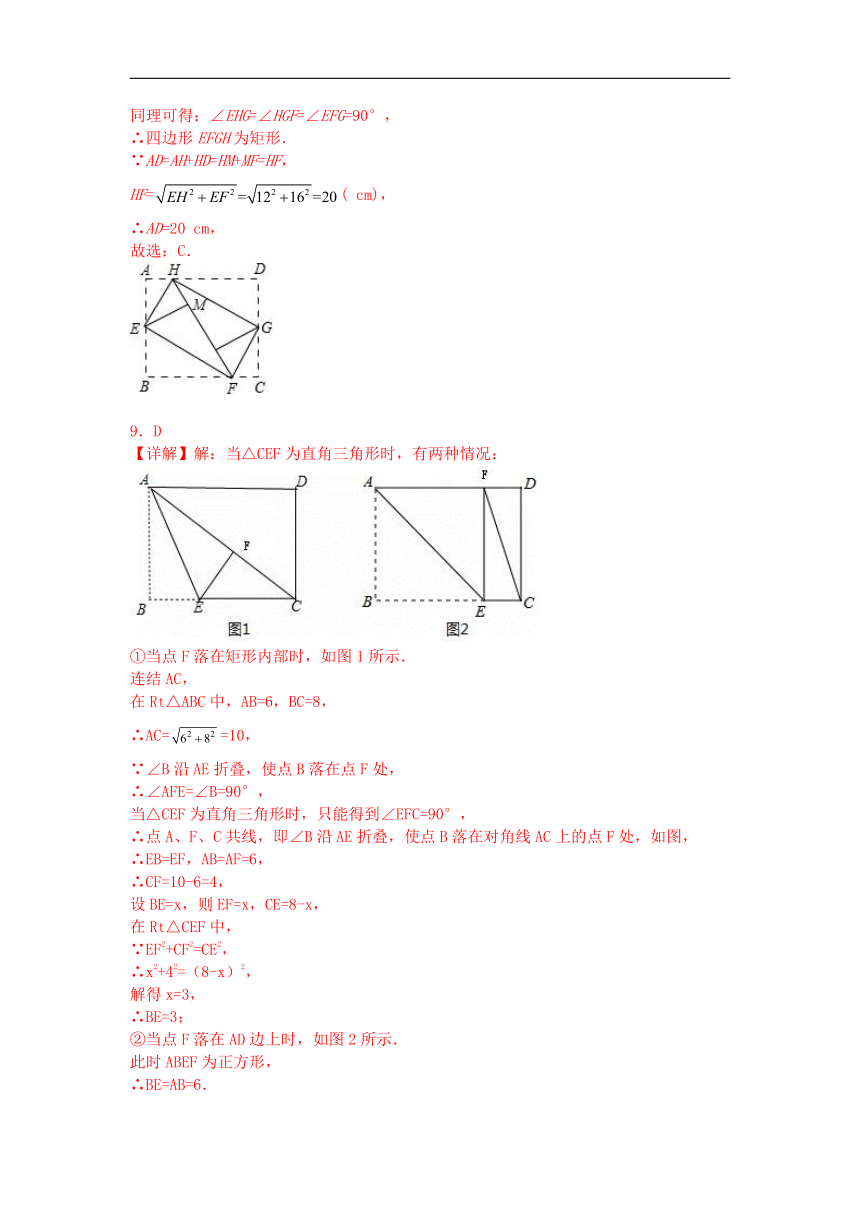
7.E为矩形ABCD的边CD上的一点,AB=AE=4,BC=2,则∠BEC是( ).
A.15° B.30° C.60° D.75°
8.如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( )
A.12cm B.16cm C.20cm D.28cm
9.如图,在矩形中,,,点是边上一点,将沿折叠,使点落在点处.连结,当为直角三角形时,的长是( )
A. B. C.或 D.或
10.如图,在矩形ABCD中,AB=8,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图②,折痕为MN,连接ME,NE;第二次折叠纸片使点N与点E重合,如图③,点B落到B′处,折痕为HG,连接HE,则下列结论:①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,中,,,,是的中点,是的中点,于点,则的长是______.
12.如图,在矩形中,对角线,相交于点,,垂直平分于点,则的长为__________.
13.如图所示,矩形中,,,点在边上,若平分,则的长是______.
14.如图,在矩形中,,,为线段上一动点,于点,于点,则的最小值为 _____.
15.如图,在平面直角坐标系中有一矩形,其中,,.若将沿所在直线翻折,点B落在点E处,则E点的坐标是________.
三、解答题
16.如图所示,四边形OABC是长方形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,已知长方形OABC的周长为16.
(1)若OA长为x,则B点坐标为_____;
(2)若A点坐标为(5,0),求点D和点E的坐标.
17.如图所示,是两种长方形铝合金窗框.已知窗框的长都是y米,窗框宽都是x米,若一用户需(1)型窗框3个,(2)型的窗框4个,则:
(1)共需铝合金多少米?(用含有x,y的式子表示)
(2)若x=0.8米,y=1.2米,则共需铝合金多少米?
18.在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.
(1)求证:四边形AFCE是平行四边形;
(2)若AE⊥BD,AF=3,AB=4,求BF的长度.
参考答案
1.C
【详解】解:∵AC⊥BC,
∴∠ACB=90°,
∵M为AB的中点,
∴CM=AB,
∵AB=,
∴CM=,
故选C.
2.C
【详解】解:∵纸条两边互相平行,
∴∠1+∠2=∠ABC=120°,
由翻折变换的性质得,∠1=∠2,
∴∠1=60°.
故选C.
3.C
【详解】解:∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OB,
∵∠AOD=60°,
∴△AOD是等边三角形,
∴OA=OD=AD=3,
∴BD=2OD=6,
∴AB==3.
故选:C.
4.C
【详解】解:A、当∠A+∠B=180°时,不可判断平行四边形ABCD成为矩形;
B、当∠B+∠C=180°时,不可判断平行四边形ABCD成为矩形;
C、当∠A=∠B时,∠A=∠B=90°,可判定平行四边形ABCD是矩形;
D、当∠B=∠D时,不可判断平行四边形ABCD是矩形;
故选:C.
5.B
【详解】解:根据尺规作图可知EF是AB的垂直平分线,
∴D是AB中点,
∴CD=CG=,
∴CG:AB=:AB=1:2,
故选B.
6.A
【详解】解:四边形为矩形,
,,,
矩形纸片沿对角线折叠,点落在点处,
,
,
,
,
,
设,则,,
在中,,
,
解得,
,
的面积.
故选:.
7.D
【详解】∵在Rt△ADE中,AD=2,AE=4,
∴∠AED=30°,
∵AB∥CD,∴∠EAB=∠AED=30°,
∵AB=AE,
∴∠AEB=75°,
∴∠BEC=180°-∠AED-∠AEB=180°-30°-75°=75°.
故选D.
8.C
【详解】解:如图,
根据题意得:∠HEM=∠AEH,∠BEF=∠FEM,
∴∠HEF=∠HEM+∠FEM=×180°=90°,
同理可得:∠EHG=∠HGF=∠EFG=90°,
∴四边形EFGH为矩形.
∵AD=AH+HD=HM+MF=HF,
HF=( cm),
∴AD=20 cm,
故选:C.
9.D
【详解】解:当△CEF为直角三角形时,有两种情况:
①当点F落在矩形内部时,如图1所示.
连结AC,
在Rt△ABC中,AB=6,BC=8,
∴AC==10,
∵∠B沿AE折叠,使点B落在点F处,
∴∠AFE=∠B=90°,
当△CEF为直角三角形时,只能得到∠EFC=90°,
∴点A、F、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点F处,如图,
∴EB=EF,AB=AF=6,
∴CF=10-6=4,
设BE=x,则EF=x,CE=8-x,
在Rt△CEF中,
∵EF2+CF2=CE2,
∴x2+42=(8-x)2,
解得x=3,
∴BE=3;
②当点F落在AD边上时,如图2所示.
此时ABEF为正方形,
∴BE=AB=6.
综上所述,BE的长为3或6.
故选D.
10.C
【详解】解:如图③,由折叠可得,∠MEN=∠A=90°,HG⊥NE,即ME⊥EN,HG⊥EN,∴EM∥GH,故①正确;
∵EM∥GH,∴∠NME=∠NHG,由折叠可得,∠NME=∠AMN,∠EHG=∠NHG,∴∠AMN=∠EHG,故③正确;
如图2,作NF⊥CD于F.设DM=x,则AM=EM=10﹣x.∵点E是CD的中点,AB=CD=,∴DE=CD=.在Rt△DEM中,∵DM2+DE2=EM2,∴()2+x2=(10﹣x)2,解得x=2.6,∴DM=2.6,AM=EM=7.4.∵∠DEM+∠NEF=90°,∠NEF+∠ENF=90°,∴∠DEM=∠ENF.∵∠D=∠EFN=90°,∴△DME∽△FEN,∴,即,∴EN=,∴AN=,∴tan∠AMN==,∴tan∠EHG=,故④正确;
又∵tan60°=>,∴∠AMN≠60°,即∠EMH≠60°,∴△MEH不是等边三角形,故②错误,∴正确的结论有3个.故选C.
11.
【详解】解:∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB==10,
∵D是AB的中点,
∴BD=DC=AD=5,= ,
连接DE,
∵E是BC的中点,
∴=6,
∵,
∴.
故答案为:.
12.
【详解】∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵AE垂直平分OB,
∴AB=AO,
∴OA=AB=OB=3,
∴BD=2OB=6,
∴AD==;
故答案为:.
13.
【详解】解:过点作于
四边形是矩形
,,
平分
,
又,
,,
,
,、
,
在中,
故答案为:
14.
【详解】解:如图,连接,
于点,于点,
,
四边形是矩形,
,,,
四边形是矩形,
,
由勾股定理得:,
当时,最小,则最小,
此时,,
即,
,
的最小值为,
故答案为:.
15.
【详解】过E作轴于点M,过E作于F,连接交于点G,如下图.
由对称性可知,,,
由题意可知,
∵,
∴是等腰三角形,,
∴,
∵,,,
∴,,
∵四边形是矩形,,
∴,,
∵,,,
∴
∵,
,,,
∴,
∵,,
∴,
∵,,,,
∴,
解得:,
∵,,,
∴,
∵,,
∴E点坐标为.
故答案为:.
16.
【详解】(1)长方形OABC周长=16,
则OA+AB=8
OA=x,AB=8-x
B点坐标为(x,8-x)
(2)∵矩形OABC的周长为16,
∴2OA+2OC=16,
∵A点坐标为(5,0),
∴OA=5,
∴OC=3,
∵在Rt△ABE中,∠B=90°,AB=3,AE=OA=5,由勾股定理得:BE=4,
∴CE=5-4=1,
设OD=x,则DE=OD=x,DC=3-x,
在Rt△CDE中,由勾股定理得:x2=12+(3-x)2,
解得:x=
即OD=
∴D的坐标是(0,),E的坐标是(1,3).
17.
【详解】(1)一个(1)型窗框材料为(2y+3x)米,一个(2)型窗框材料为(2y+2x)米,
共需铝合金为:3(2y+3x)+4(2y+2x)=6y+9x+8y+8x=(17x+14y)米,
(2)当x=0.8米,y=1.2米时,
原式=17×0.8+14×1.2=13.6+16.8=30.4米.
18.
【详解】(1)证明:如图所示,连接AC,交BD于O,
∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC,OB=OD,
∵DE=FB,
∴OE=OF,
∴四边形AFCE是平行四边形;
(2)解:∵DE=EF=BF,AE⊥BD,
∴AD=AF=3,
∴BD=,
∴BF=BD=.
一、单选题
1.如图,公路AC,BC互相垂直,公路AB的中点M与点C被湖隔开,若测得AB的长为2.8km,则M,C两点间的距离为( )
A.1.5km B.2.8km C.1.4km D.1.9km
2.如图:一张宽度相等的纸条折叠后,若∠ABC=120°,则∠1的度数是( )
A.80° B.70° C.60° D.50°
3.如图,矩形ABCD的对角线AC,BD相交于点O,AD=3,∠AOD=60°,则AB的长为( )
A.3 B.2 C.3 D.6
4.要使平行四边形成为矩形,需要添加的条件是( )
A. B. C. D.
5.在中,,分别以A点,B点为圆心以大于为半径画弧,两弧交于E,F,连接交于点D,连接,以C为圆心,长为半径作弧,交于G点,则( )
A. B.1:2 C. D.
6.如图在矩形中,,,将沿对角线翻折,点落在点处,交于点,则的面积为( )
A. B. C.21 D.24
7.E为矩形ABCD的边CD上的一点,AB=AE=4,BC=2,则∠BEC是( ).
A.15° B.30° C.60° D.75°
8.如图,小明同学在将一张矩形纸片ABCD的四个角向内折起时,发现恰好能拼成一个无缝隙无重叠的四边形EFGH.于是他测量出EH=12cm,EF=16cm,根据这两个数据他很快求出了边AD的长,则边AD的长是( )
A.12cm B.16cm C.20cm D.28cm
9.如图,在矩形中,,,点是边上一点,将沿折叠,使点落在点处.连结,当为直角三角形时,的长是( )
A. B. C.或 D.或
10.如图,在矩形ABCD中,AB=8,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图②,折痕为MN,连接ME,NE;第二次折叠纸片使点N与点E重合,如图③,点B落到B′处,折痕为HG,连接HE,则下列结论:①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=.其中正确的个数是( )
A.1个 B.2个 C.3个 D.4个
二、填空题
11.如图,中,,,,是的中点,是的中点,于点,则的长是______.
12.如图,在矩形中,对角线,相交于点,,垂直平分于点,则的长为__________.
13.如图所示,矩形中,,,点在边上,若平分,则的长是______.
14.如图,在矩形中,,,为线段上一动点,于点,于点,则的最小值为 _____.
15.如图,在平面直角坐标系中有一矩形,其中,,.若将沿所在直线翻折,点B落在点E处,则E点的坐标是________.
三、解答题
16.如图所示,四边形OABC是长方形,点D在OC边上,以AD为折痕,将△OAD向上翻折,点O恰好落在BC边上的点E处,已知长方形OABC的周长为16.
(1)若OA长为x,则B点坐标为_____;
(2)若A点坐标为(5,0),求点D和点E的坐标.
17.如图所示,是两种长方形铝合金窗框.已知窗框的长都是y米,窗框宽都是x米,若一用户需(1)型窗框3个,(2)型的窗框4个,则:
(1)共需铝合金多少米?(用含有x,y的式子表示)
(2)若x=0.8米,y=1.2米,则共需铝合金多少米?
18.在矩形ABCD中,点E,点F为对角线BD上两点,DE=EF=FB.
(1)求证:四边形AFCE是平行四边形;
(2)若AE⊥BD,AF=3,AB=4,求BF的长度.
参考答案
1.C
【详解】解:∵AC⊥BC,
∴∠ACB=90°,
∵M为AB的中点,
∴CM=AB,
∵AB=,
∴CM=,
故选C.
2.C
【详解】解:∵纸条两边互相平行,
∴∠1+∠2=∠ABC=120°,
由翻折变换的性质得,∠1=∠2,
∴∠1=60°.
故选C.
3.C
【详解】解:∵四边形ABCD是矩形,
∴∠DAB=90°,OA=OD=OB,
∵∠AOD=60°,
∴△AOD是等边三角形,
∴OA=OD=AD=3,
∴BD=2OD=6,
∴AB==3.
故选:C.
4.C
【详解】解:A、当∠A+∠B=180°时,不可判断平行四边形ABCD成为矩形;
B、当∠B+∠C=180°时,不可判断平行四边形ABCD成为矩形;
C、当∠A=∠B时,∠A=∠B=90°,可判定平行四边形ABCD是矩形;
D、当∠B=∠D时,不可判断平行四边形ABCD是矩形;
故选:C.
5.B
【详解】解:根据尺规作图可知EF是AB的垂直平分线,
∴D是AB中点,
∴CD=CG=,
∴CG:AB=:AB=1:2,
故选B.
6.A
【详解】解:四边形为矩形,
,,,
矩形纸片沿对角线折叠,点落在点处,
,
,
,
,
,
设,则,,
在中,,
,
解得,
,
的面积.
故选:.
7.D
【详解】∵在Rt△ADE中,AD=2,AE=4,
∴∠AED=30°,
∵AB∥CD,∴∠EAB=∠AED=30°,
∵AB=AE,
∴∠AEB=75°,
∴∠BEC=180°-∠AED-∠AEB=180°-30°-75°=75°.
故选D.
8.C
【详解】解:如图,
根据题意得:∠HEM=∠AEH,∠BEF=∠FEM,
∴∠HEF=∠HEM+∠FEM=×180°=90°,
同理可得:∠EHG=∠HGF=∠EFG=90°,
∴四边形EFGH为矩形.
∵AD=AH+HD=HM+MF=HF,
HF=( cm),
∴AD=20 cm,
故选:C.
9.D
【详解】解:当△CEF为直角三角形时,有两种情况:
①当点F落在矩形内部时,如图1所示.
连结AC,
在Rt△ABC中,AB=6,BC=8,
∴AC==10,
∵∠B沿AE折叠,使点B落在点F处,
∴∠AFE=∠B=90°,
当△CEF为直角三角形时,只能得到∠EFC=90°,
∴点A、F、C共线,即∠B沿AE折叠,使点B落在对角线AC上的点F处,如图,
∴EB=EF,AB=AF=6,
∴CF=10-6=4,
设BE=x,则EF=x,CE=8-x,
在Rt△CEF中,
∵EF2+CF2=CE2,
∴x2+42=(8-x)2,
解得x=3,
∴BE=3;
②当点F落在AD边上时,如图2所示.
此时ABEF为正方形,
∴BE=AB=6.
综上所述,BE的长为3或6.
故选D.
10.C
【详解】解:如图③,由折叠可得,∠MEN=∠A=90°,HG⊥NE,即ME⊥EN,HG⊥EN,∴EM∥GH,故①正确;
∵EM∥GH,∴∠NME=∠NHG,由折叠可得,∠NME=∠AMN,∠EHG=∠NHG,∴∠AMN=∠EHG,故③正确;
如图2,作NF⊥CD于F.设DM=x,则AM=EM=10﹣x.∵点E是CD的中点,AB=CD=,∴DE=CD=.在Rt△DEM中,∵DM2+DE2=EM2,∴()2+x2=(10﹣x)2,解得x=2.6,∴DM=2.6,AM=EM=7.4.∵∠DEM+∠NEF=90°,∠NEF+∠ENF=90°,∴∠DEM=∠ENF.∵∠D=∠EFN=90°,∴△DME∽△FEN,∴,即,∴EN=,∴AN=,∴tan∠AMN==,∴tan∠EHG=,故④正确;
又∵tan60°=>,∴∠AMN≠60°,即∠EMH≠60°,∴△MEH不是等边三角形,故②错误,∴正确的结论有3个.故选C.
11.
【详解】解:∵在Rt△ABC中,∠ACB=90°,AC=6,BC=8,
∴AB==10,
∵D是AB的中点,
∴BD=DC=AD=5,= ,
连接DE,
∵E是BC的中点,
∴=6,
∵,
∴.
故答案为:.
12.
【详解】∵四边形ABCD是矩形,
∴OB=OD,OA=OC,AC=BD,
∴OA=OB,
∵AE垂直平分OB,
∴AB=AO,
∴OA=AB=OB=3,
∴BD=2OB=6,
∴AD==;
故答案为:.
13.
【详解】解:过点作于
四边形是矩形
,,
平分
,
又,
,,
,
,、
,
在中,
故答案为:
14.
【详解】解:如图,连接,
于点,于点,
,
四边形是矩形,
,,,
四边形是矩形,
,
由勾股定理得:,
当时,最小,则最小,
此时,,
即,
,
的最小值为,
故答案为:.
15.
【详解】过E作轴于点M,过E作于F,连接交于点G,如下图.
由对称性可知,,,
由题意可知,
∵,
∴是等腰三角形,,
∴,
∵,,,
∴,,
∵四边形是矩形,,
∴,,
∵,,,
∴
∵,
,,,
∴,
∵,,
∴,
∵,,,,
∴,
解得:,
∵,,,
∴,
∵,,
∴E点坐标为.
故答案为:.
16.
【详解】(1)长方形OABC周长=16,
则OA+AB=8
OA=x,AB=8-x
B点坐标为(x,8-x)
(2)∵矩形OABC的周长为16,
∴2OA+2OC=16,
∵A点坐标为(5,0),
∴OA=5,
∴OC=3,
∵在Rt△ABE中,∠B=90°,AB=3,AE=OA=5,由勾股定理得:BE=4,
∴CE=5-4=1,
设OD=x,则DE=OD=x,DC=3-x,
在Rt△CDE中,由勾股定理得:x2=12+(3-x)2,
解得:x=
即OD=
∴D的坐标是(0,),E的坐标是(1,3).
17.
【详解】(1)一个(1)型窗框材料为(2y+3x)米,一个(2)型窗框材料为(2y+2x)米,
共需铝合金为:3(2y+3x)+4(2y+2x)=6y+9x+8y+8x=(17x+14y)米,
(2)当x=0.8米,y=1.2米时,
原式=17×0.8+14×1.2=13.6+16.8=30.4米.
18.
【详解】(1)证明:如图所示,连接AC,交BD于O,
∵四边形ABCD是矩形,
∴∠BAD=90°,OA=OC,OB=OD,
∵DE=FB,
∴OE=OF,
∴四边形AFCE是平行四边形;
(2)解:∵DE=EF=BF,AE⊥BD,
∴AD=AF=3,
∴BD=,
∴BF=BD=.
