5.1.3同位角、内错角、同旁内角课件
文档属性
| 名称 | 5.1.3同位角、内错角、同旁内角课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-22 11:06:46 | ||
图片预览




文档简介
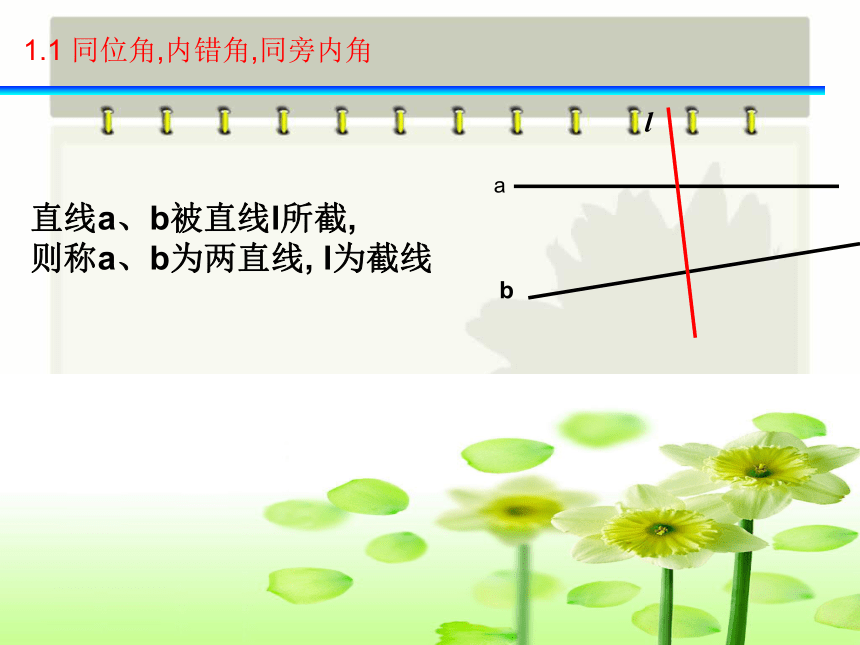
课件24张PPT。1.2 同位角、内错角、同旁内角学.科.网1.2 同位角,内错角,同旁内角一、创设情景直线a、b被直线l所截,
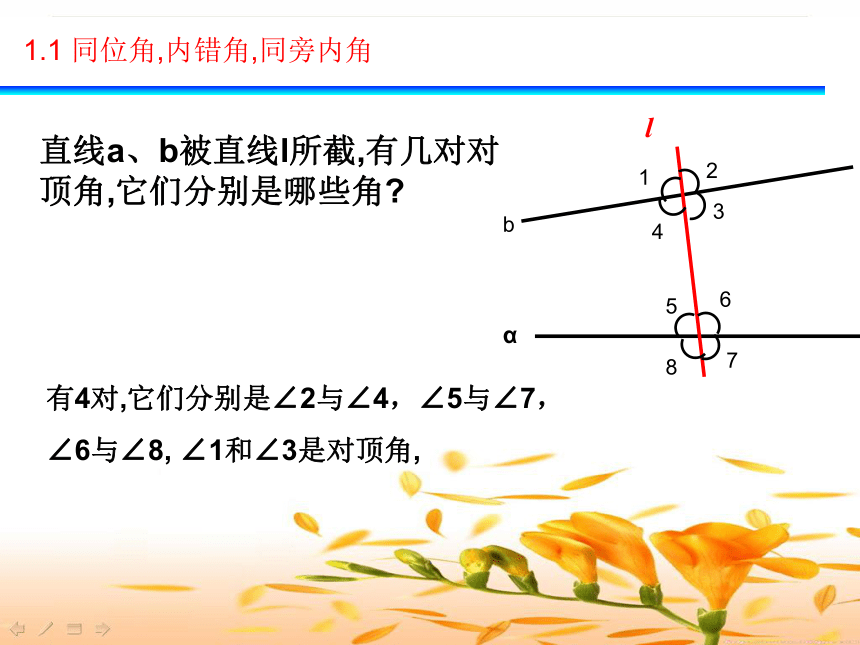
则称a、b为两直线, l为截线1.1 同位角,内错角,同旁内角有4对,它们分别是∠2与∠4,∠5与∠7,
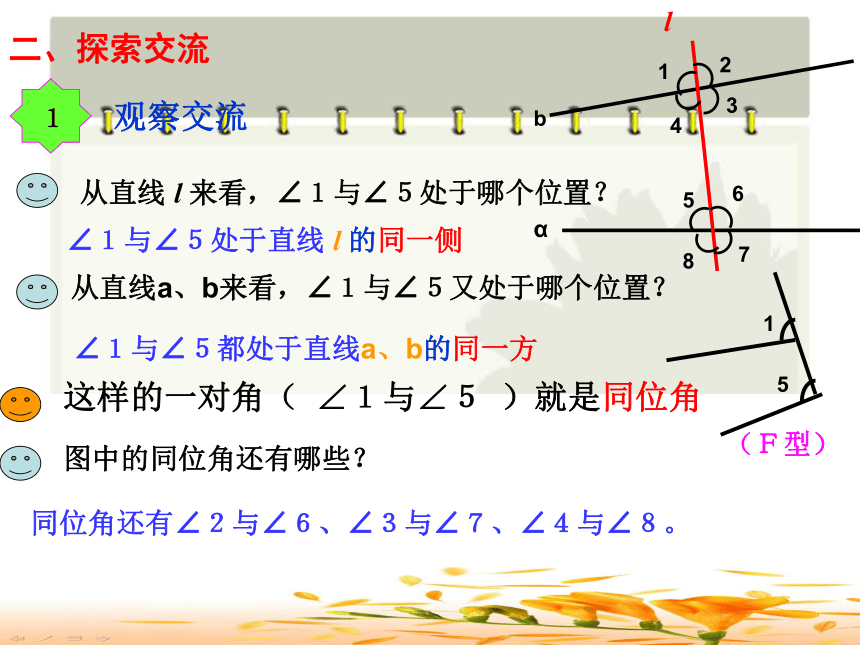
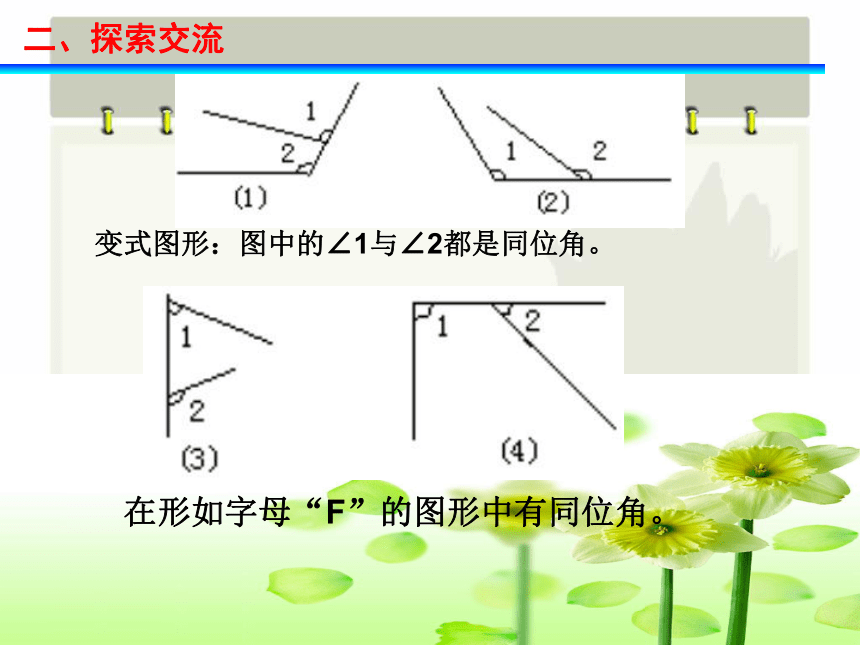
∠6与∠8, ∠1和∠3是对顶角, 1.1 同位角,内错角,同旁内角直线a、b被直线l所截,有几对对顶角,它们分别是哪些角?学.科.网二、探索交流∠1与∠5处于直线 l 的同一侧∠1与∠5都处于直线a、b的同一方同位角还有∠2与∠6、∠3与∠7、∠4与∠8。(F型)在形如字母“F”的图形中有同位角。 变式图形:图中的∠1与∠2都是同位角。二、探索交流二、类比交流∠4与∠6都处于直线 l 的两侧∠4与∠6都处于直线a、b的内部内错角还有∠3与∠5。(Z型)变式图形:图中的∠1与∠2都是内错角学.科.网图形特征:在形如“Z”的图形中有内错角。二、探索交流二、类比交流∠4与∠5处于直线 l 的同一侧∠4与∠5都处于直线a、b的内部同旁内角还有∠3与∠6。(方框形)变式图形:图中的∠1与∠2都是同旁内角。图形特征:在形如“方框形”的图形中有同旁内角。 二、探索交流辩一辩两直线同侧两直线之间两直线之间截线的同旁截线异侧截线同侧归纳:寻找同位角,内错角,同旁内角关键要分清
两条直线和截线,然后按相互的位置特征进行判别 做一做:
请用三根竹条或小木棍制作一个如图的风筝骨架,观察风筝骨架中有几个角,请把它画成几何图形,并用符号表示这些角,然后分别指出所有的对顶角,同位角,内错角,同旁内角三、联系生活解 放 路交通指南鞍马池路民人飞机场2、根据地图显示填空:学校与游乐场所在的角形成一对( )
学校与超市所在的角形成一对( )
学校与飞机场所在的角形成一对( )同位角同旁内角内错角路 如图,直线a截直线b,直线c所得的同位角有______对,它们是______________________________________________;
内错角有______对,它们是______________________;
同旁内角有_____对,它们是______________________。?1与?3, ?2与?4, ?5与?7, ?6与?842?2与?7, ?3与?62?2与 ?3, ?6与 ?7练习例1.如图,直线DE截AB ,AC,构成8个角,
指出所有的同位角,内错角,同旁内角
(1)解:两条直线是AB,AC,截线是DE,所以8个角中同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3内错角:∠4与∠5,∠1与∠6, 同旁内角:∠1与∠5,∠4与∠6。四、例题精讲(3)归纳:两个角若有一边在同一直线上,这条直线就是截线,其余两边所在的直线是两直线(AB与DE 被AC所截,是内错角)∠A与∠6呢?∠A与∠5呢?(AB与DE 被AC所截,是同旁内角)(AB与DE 被AC所截,是同位角)(2)变式:∠A与∠8是哪两条直线被第3条直线所截的角?
它们是什么关系的角?
四、例题精讲练习(1)课内练习1
(2)合作学习分析:如果∠1=∠2,由对顶角相等,得∠2=∠4,
那么∠1=∠4,因为∠2与∠3互补,即∠2+∠3= 180°,又因为∠1=∠2,所以∠1+∠3=180°,
即∠1和∠3互补。例2:如图,直线DE交∠ABC的边BA于点F,如果 ∠1=∠2,那么同位角∠1和∠4相等,同旁内角∠1和∠3互补。请说明理由四、例题精讲练习:(1)课内练习2
(2)作业题五、小结2、掌握辩别这些角的关键是看哪两条直线被哪一条直线所截、分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角。(1)同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,究其实质,它们主要是反映了直线相交产生的角中,相互位置所具有的特征:(1)两个同位角就是与直线的位置关系而言具有“同上、同右”、“同上、同左”“同下、同右”或“同下、同左”的特征。(2)内错角具有“同内、异侧”的特征。(3)同旁内角具有“同内、同侧”的特征。六、作业:1、作 业 本
则称a、b为两直线, l为截线1.1 同位角,内错角,同旁内角有4对,它们分别是∠2与∠4,∠5与∠7,
∠6与∠8, ∠1和∠3是对顶角, 1.1 同位角,内错角,同旁内角直线a、b被直线l所截,有几对对顶角,它们分别是哪些角?学.科.网二、探索交流∠1与∠5处于直线 l 的同一侧∠1与∠5都处于直线a、b的同一方同位角还有∠2与∠6、∠3与∠7、∠4与∠8。(F型)在形如字母“F”的图形中有同位角。 变式图形:图中的∠1与∠2都是同位角。二、探索交流二、类比交流∠4与∠6都处于直线 l 的两侧∠4与∠6都处于直线a、b的内部内错角还有∠3与∠5。(Z型)变式图形:图中的∠1与∠2都是内错角学.科.网图形特征:在形如“Z”的图形中有内错角。二、探索交流二、类比交流∠4与∠5处于直线 l 的同一侧∠4与∠5都处于直线a、b的内部同旁内角还有∠3与∠6。(方框形)变式图形:图中的∠1与∠2都是同旁内角。图形特征:在形如“方框形”的图形中有同旁内角。 二、探索交流辩一辩两直线同侧两直线之间两直线之间截线的同旁截线异侧截线同侧归纳:寻找同位角,内错角,同旁内角关键要分清
两条直线和截线,然后按相互的位置特征进行判别 做一做:
请用三根竹条或小木棍制作一个如图的风筝骨架,观察风筝骨架中有几个角,请把它画成几何图形,并用符号表示这些角,然后分别指出所有的对顶角,同位角,内错角,同旁内角三、联系生活解 放 路交通指南鞍马池路民人飞机场2、根据地图显示填空:学校与游乐场所在的角形成一对( )
学校与超市所在的角形成一对( )
学校与飞机场所在的角形成一对( )同位角同旁内角内错角路 如图,直线a截直线b,直线c所得的同位角有______对,它们是______________________________________________;
内错角有______对,它们是______________________;
同旁内角有_____对,它们是______________________。?1与?3, ?2与?4, ?5与?7, ?6与?842?2与?7, ?3与?62?2与 ?3, ?6与 ?7练习例1.如图,直线DE截AB ,AC,构成8个角,
指出所有的同位角,内错角,同旁内角
(1)解:两条直线是AB,AC,截线是DE,所以8个角中同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3内错角:∠4与∠5,∠1与∠6, 同旁内角:∠1与∠5,∠4与∠6。四、例题精讲(3)归纳:两个角若有一边在同一直线上,这条直线就是截线,其余两边所在的直线是两直线(AB与DE 被AC所截,是内错角)∠A与∠6呢?∠A与∠5呢?(AB与DE 被AC所截,是同旁内角)(AB与DE 被AC所截,是同位角)(2)变式:∠A与∠8是哪两条直线被第3条直线所截的角?
它们是什么关系的角?
四、例题精讲练习(1)课内练习1
(2)合作学习分析:如果∠1=∠2,由对顶角相等,得∠2=∠4,
那么∠1=∠4,因为∠2与∠3互补,即∠2+∠3= 180°,又因为∠1=∠2,所以∠1+∠3=180°,
即∠1和∠3互补。例2:如图,直线DE交∠ABC的边BA于点F,如果 ∠1=∠2,那么同位角∠1和∠4相等,同旁内角∠1和∠3互补。请说明理由四、例题精讲练习:(1)课内练习2
(2)作业题五、小结2、掌握辩别这些角的关键是看哪两条直线被哪一条直线所截、分清哪一条直线截哪两条直线形成了哪些角,是作出正确判定的前提,在截线的同旁找同位角,同旁内角,在截线的不同旁,找内错角。(1)同位角、内错角、同旁内角都是两条直线被第三条直线所截时产生的,究其实质,它们主要是反映了直线相交产生的角中,相互位置所具有的特征:(1)两个同位角就是与直线的位置关系而言具有“同上、同右”、“同上、同左”“同下、同右”或“同下、同左”的特征。(2)内错角具有“同内、异侧”的特征。(3)同旁内角具有“同内、同侧”的特征。六、作业:1、作 业 本
