5.1.2垂线课件
图片预览








文档简介
(共35张PPT)
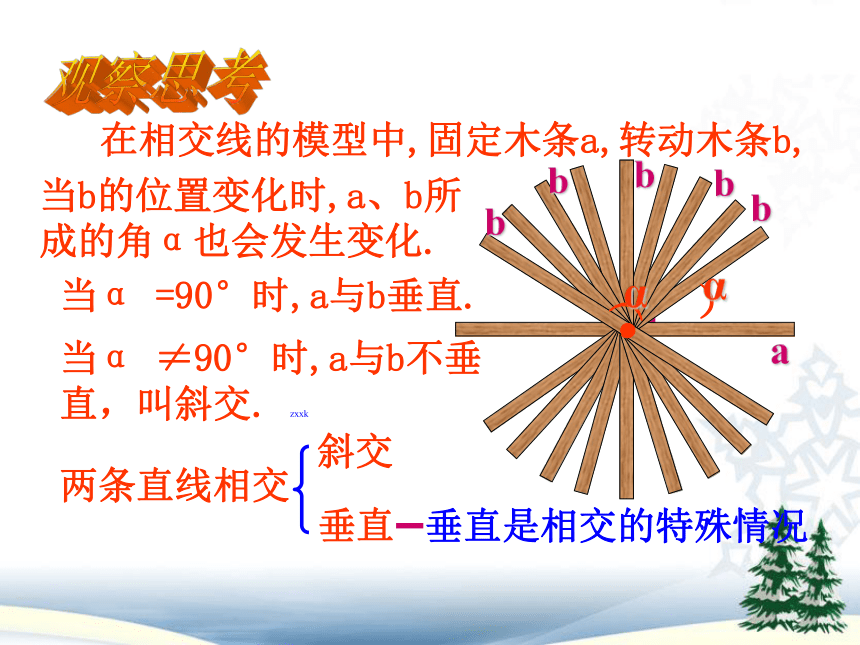
在相交线的模型中,固定木条a,转动木条b,
当α
=90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α
≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。
一、垂直的定义
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。
哪一组中的两条直线互相垂直?
×
×
日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.
你能再举出其他例子吗?
比如:教室的门.窗.黑板以及我们见过的梯子.天安门广场的旗杆.城市的立交桥.体操运动员参加的吊环比赛.
红十字.测量跳远成绩等等.
b
a
用“⊥”和直线字母表示垂直
O
α
2.垂直的表示:
例如、如图,a、b互相垂直,
垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b,
垂足为O.
书写形式
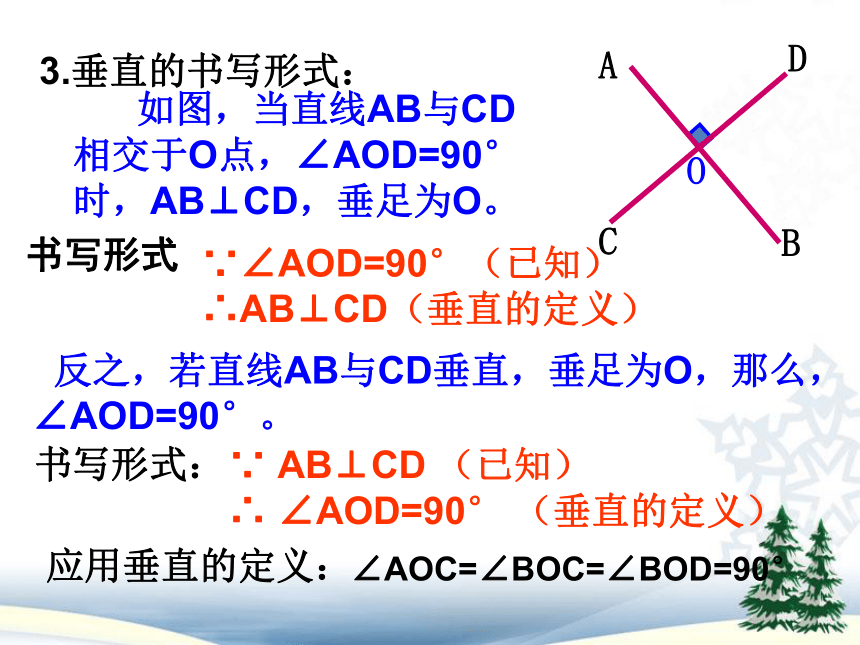
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。
∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)
书写形式:
反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。
3.垂直的书写形式:
∵
AB⊥CD
(已知)
∴
∠AOD=90°
(垂直的定义)
应用垂直的定义:
∠AOC=∠BOC=∠BOD=90°
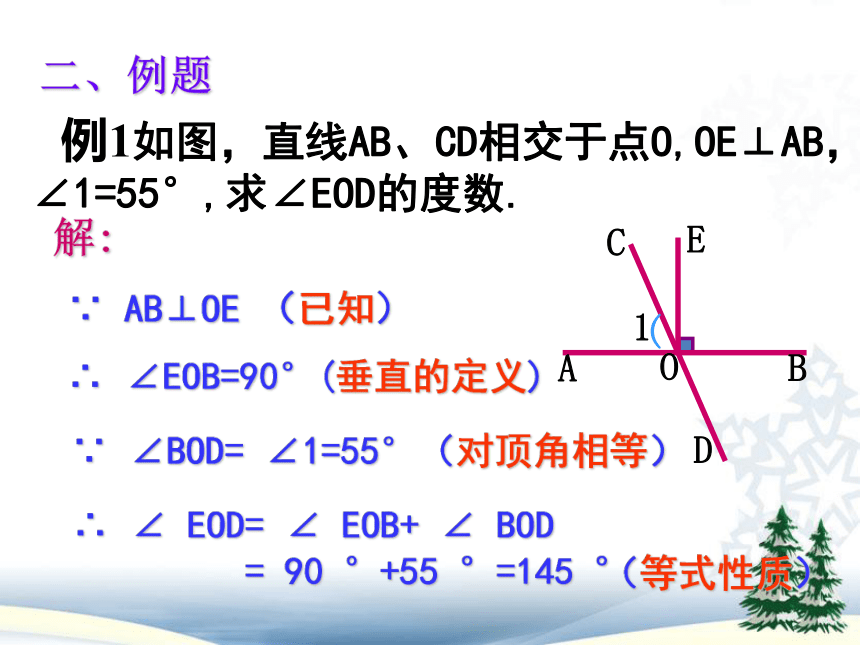
例1如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
A
C
E
B
D
O
1
∴
∠EOB=90°(垂直的定义)
∴
∠
EOD=
∠
EOB+
∠
BOD
=
90
°+55
°=145
°
(
解:
∵
AB⊥OE
(已知)
∵
∠BOD=
∠1=55°(对顶角相等)
二、例题
(等式性质)
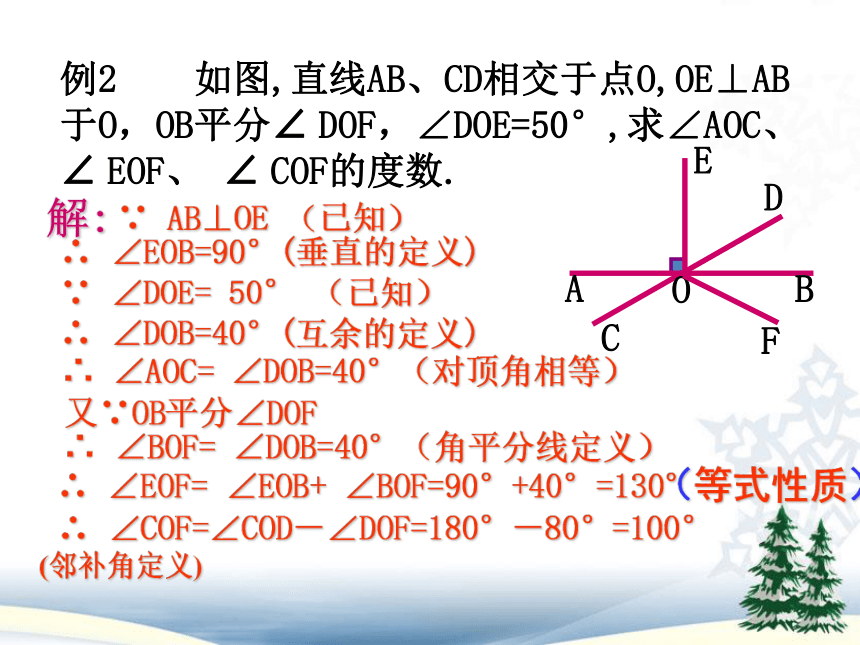
例2
如图,直线AB、CD相交于点O,OE⊥AB于O,OB平分∠
DOF,∠DOE=50°,求∠AOC、
∠
EOF、
∠
COF的度数.
A
C
E
B
D
O
∴
∠EOB=90°(垂直的定义)
∴
∠COF=∠COD-∠DOF=180°-80°=100°
(邻补角定义)
解:
∵
AB⊥OE
(已知)
∴
∠AOC=
∠DOB=40°(对顶角相等)
F
∵
∠DOE=
50°
(已知)
∴
∠DOB=40°(互余的定义)
又∵OB平分∠DOF
∴
∠BOF=
∠DOB=40°(角平分线定义)
∴
∠EOF=
∠EOB+
∠BOF=90°+40°=130°
(等式性质)
学生练习:
如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,求∠COE的度数.
A
C
E
B
D
O
1
)
三、垂线的画法
问题:
怎么样画垂线?
1.垂线的画法:
问题:
这样画l的垂线可以画几条?
1放、
2靠、
3画线、
l
O
如图,已知直线
l,作l的垂线。
工具:直尺、三角板
A
无数条
1.垂线的画法:
l
A
如图,已知直线
l
和l上的一点A
,过点A作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是过点A的直线l的垂线.
1.垂线的画法:
l
A
如图,已知直线
l
和l外的一点A
,过点A作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是过点A的直线l的垂线.
请同学们画一下
结论:
过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题:过已知直线
l
和l上(或外)的一点A
,
作l的垂线,可以作几条?
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
垂线的唯一性.
E
E
E
注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.
经过直线AB外一点P,在同一平面内量角器,画出垂直于直线AB的直线.
.
P
A
B
做一做
我们可以用三角板来画垂线,那还有其他的画法吗?
此问题就是“直线外一点与已知直线上各点所连的线段中,有没有最短的线段?”
P
请你画图,并用尺量一下,看看哪一条线段最短?
垂线段的概念:
由直线外一点向直线引垂线,这点与垂足间的线段叫做垂线段。
P
l
A
要找垂线段,
先把点来看。
过点画垂线,
点足垂线段。
例如:如图,PA⊥l于点A
,线段PA叫做点P到直线l的垂线段.
结论:
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:
垂线段最短.
如下图所示,AB与直线BC垂直,点A与直线BC上的各点的距离中,最短的是哪条线段?
A
B
.
C
∟
点A到点B的
距离最短
找一找
垂线的性质的应用
某村在如图所示的河边,为解决村庄供水问题,需把河中水引到村庄A处,在河岸CD的什么地方搭设管道,才能使用的管道最短?画出图来,并说明道理.
小
河
C
D
.
村庄
∟
做一做
根据垂线段
最短的性质得到.
点到直线的距离:
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
l
A
例如:如图,PA⊥l于点A
,垂线段PA的长度叫做点P到直线l的距离.
体育课上我们怎么测量“跳远成绩”的?测量时皮尺与踏板之间应保持什么位置关系?为什么?
那么,如果你是运动员,怎么跳成绩最佳?(结合垂线段、斜线段的长度考虑)
A
B
解:过A点作AB⊥l于点B
,垂线段AB的长度就是该同学的跳远成绩.
1.
理解了垂线的概念,会用三角尺、量角器过一点画一条直线的垂线;
2.
理解了点到直线的距离的概念,并会度量点到直线的距离。
3.
掌握了垂线的两条性质.
反思收获
垂线的定义有以下两层含义:
1、∵AB⊥CD(已知)
∴∠1=90°(垂线的定义)
2、∵∠1=90°(已知)
∴AB⊥CD(垂线的定义)
归纳小结
画垂线的方法
画垂线的方法可归纳为“一落、二过、三画”
1.一落:把三角尺的一条直角边落在已知直线上;
2.二过:让三角尺的另一条直角边经过已知的点.
3.三画:沿着直角边经过已知点画直线。
归纳小结
线段、射线的垂线应怎么画呢?
1.垂线的性质:在同一平面内,经过直线外或直线上一点,有且只有一条直线与已知直线垂直.(唯一性)
归纳小结
2.
直线外一点与直线上所有各点的连线中,垂线段最短.
简称:垂线段最短.(最短性)
3.点到直线的距离的概念
直线外一点到已知直线的垂线段的长度就叫做点到直线的距离。
如图,点P到直线AB的距离就是垂线段PQ的长度
归纳小结
在相交线的模型中,固定木条a,转动木条b,
当α
=90°时,a与b垂直.
当b的位置变化时,a、b所成的角α也会发生变化.
当α
≠90°时,a与b不垂直,叫斜交.
两条直线相交
斜交
垂直
垂直是相交的特殊情况
)
α
a
b
b
b
b
b
)
α
1.垂直定义:当两条直线相交所成的四个角中,有一个角是直角时,这两条直线互相垂直,其中一条直线叫另一条直线的垂线,它们的交点叫垂足。
例如、如图,a、b互相垂直,O叫垂足.a叫b的垂线,b也叫a的垂线。
一、垂直的定义
从垂直的定义可知,
判断两条直线互相垂直的关键:
只要找到两条直线相交时四个交角中一个角是直角。
哪一组中的两条直线互相垂直?
×
×
日常生活中,两条直线互相垂直的情形很常见,说出图5.1-6中的一些互相垂直的线条.
你能再举出其他例子吗?
比如:教室的门.窗.黑板以及我们见过的梯子.天安门广场的旗杆.城市的立交桥.体操运动员参加的吊环比赛.
红十字.测量跳远成绩等等.
b
a
用“⊥”和直线字母表示垂直
O
α
2.垂直的表示:
例如、如图,a、b互相垂直,
垂足为O,则记为:
a⊥b或b⊥a,
若要强调垂足,则记为:a⊥b,
垂足为O.
书写形式
如图,当直线AB与CD相交于O点,∠AOD=90°时,AB⊥CD,垂足为O。
∵∠AOD=90°(已知)
∴AB⊥CD(垂直的定义)
书写形式:
反之,若直线AB与CD垂直,垂足为O,那么,∠AOD=90°。
3.垂直的书写形式:
∵
AB⊥CD
(已知)
∴
∠AOD=90°
(垂直的定义)
应用垂直的定义:
∠AOC=∠BOC=∠BOD=90°
例1如图,直线AB、CD相交于点O,OE⊥AB,∠1=55°,求∠EOD的度数.
A
C
E
B
D
O
1
∴
∠EOB=90°(垂直的定义)
∴
∠
EOD=
∠
EOB+
∠
BOD
=
90
°+55
°=145
°
(
解:
∵
AB⊥OE
(已知)
∵
∠BOD=
∠1=55°(对顶角相等)
二、例题
(等式性质)
例2
如图,直线AB、CD相交于点O,OE⊥AB于O,OB平分∠
DOF,∠DOE=50°,求∠AOC、
∠
EOF、
∠
COF的度数.
A
C
E
B
D
O
∴
∠EOB=90°(垂直的定义)
∴
∠COF=∠COD-∠DOF=180°-80°=100°
(邻补角定义)
解:
∵
AB⊥OE
(已知)
∴
∠AOC=
∠DOB=40°(对顶角相等)
F
∵
∠DOE=
50°
(已知)
∴
∠DOB=40°(互余的定义)
又∵OB平分∠DOF
∴
∠BOF=
∠DOB=40°(角平分线定义)
∴
∠EOF=
∠EOB+
∠BOF=90°+40°=130°
(等式性质)
学生练习:
如图,直线AB、CD相交于点O,OE⊥AB,∠1=125°,求∠COE的度数.
A
C
E
B
D
O
1
)
三、垂线的画法
问题:
怎么样画垂线?
1.垂线的画法:
问题:
这样画l的垂线可以画几条?
1放、
2靠、
3画线、
l
O
如图,已知直线
l,作l的垂线。
工具:直尺、三角板
A
无数条
1.垂线的画法:
l
A
如图,已知直线
l
和l上的一点A
,过点A作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是过点A的直线l的垂线.
1.垂线的画法:
l
A
如图,已知直线
l
和l外的一点A
,过点A作l的垂线.
B
4画线:沿着三角板的另一直角边画出垂线.
1放:放直尺,直尺的一边要与已知直线重合;
3移:移动三角板到已知点;
2靠:靠三角板,把三角板的一直角边靠在直尺上;
则所画直线AB是过点A的直线l的垂线.
请同学们画一下
结论:
过一点有且只有一条直线与已知直线垂直.
能作一条,而且只能作一条.
问题:过已知直线
l
和l上(或外)的一点A
,
作l的垂线,可以作几条?
注意:
过一点画已知线段(或射线)的垂线,就是画这条线段(或射线)所在直线的垂线.
垂线的唯一性.
E
E
E
注意:画线段(或射线)的垂线时,有时要将线段延长(或将射线反向延长)后再画垂线.
经过直线AB外一点P,在同一平面内量角器,画出垂直于直线AB的直线.
.
P
A
B
做一做
我们可以用三角板来画垂线,那还有其他的画法吗?
此问题就是“直线外一点与已知直线上各点所连的线段中,有没有最短的线段?”
P
请你画图,并用尺量一下,看看哪一条线段最短?
垂线段的概念:
由直线外一点向直线引垂线,这点与垂足间的线段叫做垂线段。
P
l
A
要找垂线段,
先把点来看。
过点画垂线,
点足垂线段。
例如:如图,PA⊥l于点A
,线段PA叫做点P到直线l的垂线段.
结论:
连接直线外一点与直线上各点的所有线段中,垂线段最短.
简单说成:
垂线段最短.
如下图所示,AB与直线BC垂直,点A与直线BC上的各点的距离中,最短的是哪条线段?
A
B
.
C
∟
点A到点B的
距离最短
找一找
垂线的性质的应用
某村在如图所示的河边,为解决村庄供水问题,需把河中水引到村庄A处,在河岸CD的什么地方搭设管道,才能使用的管道最短?画出图来,并说明道理.
小
河
C
D
.
村庄
∟
做一做
根据垂线段
最短的性质得到.
点到直线的距离:
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
P
l
A
例如:如图,PA⊥l于点A
,垂线段PA的长度叫做点P到直线l的距离.
体育课上我们怎么测量“跳远成绩”的?测量时皮尺与踏板之间应保持什么位置关系?为什么?
那么,如果你是运动员,怎么跳成绩最佳?(结合垂线段、斜线段的长度考虑)
A
B
解:过A点作AB⊥l于点B
,垂线段AB的长度就是该同学的跳远成绩.
1.
理解了垂线的概念,会用三角尺、量角器过一点画一条直线的垂线;
2.
理解了点到直线的距离的概念,并会度量点到直线的距离。
3.
掌握了垂线的两条性质.
反思收获
垂线的定义有以下两层含义:
1、∵AB⊥CD(已知)
∴∠1=90°(垂线的定义)
2、∵∠1=90°(已知)
∴AB⊥CD(垂线的定义)
归纳小结
画垂线的方法
画垂线的方法可归纳为“一落、二过、三画”
1.一落:把三角尺的一条直角边落在已知直线上;
2.二过:让三角尺的另一条直角边经过已知的点.
3.三画:沿着直角边经过已知点画直线。
归纳小结
线段、射线的垂线应怎么画呢?
1.垂线的性质:在同一平面内,经过直线外或直线上一点,有且只有一条直线与已知直线垂直.(唯一性)
归纳小结
2.
直线外一点与直线上所有各点的连线中,垂线段最短.
简称:垂线段最短.(最短性)
3.点到直线的距离的概念
直线外一点到已知直线的垂线段的长度就叫做点到直线的距离。
如图,点P到直线AB的距离就是垂线段PQ的长度
归纳小结
