人教版2022--2023八年级(下)数学第十六单元质量检测试卷A(含解析)
文档属性
| 名称 | 人教版2022--2023八年级(下)数学第十六单元质量检测试卷A(含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 1011.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 21:14:38 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
人教版2022-20203年八年级(下)第十六章二次根式检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 下列运算,结果正确的是
A. B. C. D.
2. 若 成立,则 的取值范围为
A. B. C. D. 或
3. 下列二次根式中, 的同类二次根式是
A. B. C. D.
4. 下列判断正确的是
A.
B. 若 ,则
C.
D. 可以表示边长为 的等边三角形的周长
5. 下列二次根式的被开方数中,各因式指数为 的有
A. B. C. D.
6. 下列式子一定是二次根式的是
A. B. C. D.
7. 若三角形的三边长分别是 ,,,且 ,则这个三角形的周长是
A. B. C. D.
8. 在下列各组根式中,是同类二次根式的是
A. 和 B. 和
C. 和 D. 和
9. 按如图所示的程序计算,若开始输入的 值为 ,则最后输出的结果是
A. B. C. D.
10. 若 ,,则下列等式成立的是
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 若最简二次根式 与 的被开方数相同,则 .
12. ,则 的取值范围是 .
13. 代数式 在实数范围内有意义,则 的取值范围是 .
14. 计算 的结果是 .
15. .
16. 计算: .
三、解答题(共9小题;共72分)
17.(8分) 下列二次根式中哪些是最简二次根式 哪些不是 若不是,请说明理由.
();();();
();();();
();().
18. (8分)判断下列各式是不是二次根式.
(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8)(, 异号)
19.(8分) 若最简二次根式 与 是同类二次根式,求 的值.
20. (8分)计算:.
21. (8分)计算:.
22. (8分)计算:
(1).
(2).
(3).
23. (8分)计算:
(1);
(2);
(3);
(4).(结果表示为含幂的形式)
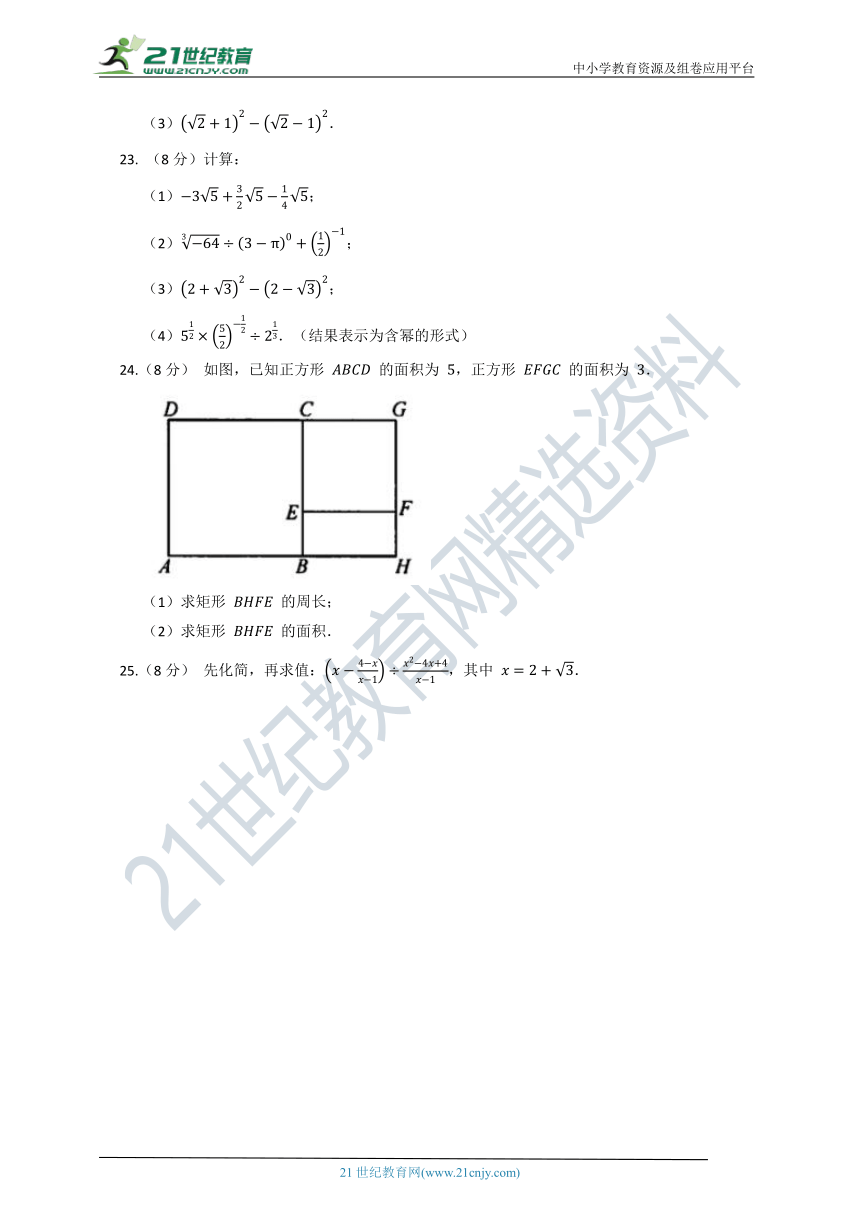
24.(8分) 如图,已知正方形 的面积为 ,正方形 的面积为 .
(1)求矩形 的周长;
(2)求矩形 的面积.
25.(8分) 先化简,再求值:,其中 .
答案
一
1. D
【解析】A. 与 不是同类二次根式,不能合并,此选项错误;
B. 与 不是同类二次根式,不能合并,此选项错误;
C.,此选项错误;
D.,此选项计算正确;
故选:D.
2. B
3. D
【解析】.
4. D
【解析】A.,
,
,故本选项错误;
B.若 ,则 或 ,故本选项错误;
C.当 , 时, 成立,故本选项错误.
5. A
【解析】A. 的被开方数的因式指数为 ,故符合题意;
B. 的被开方数的因式分别为 ,,,其中 的指数为 ,故不符合题意;
C. 的被开方数的因式有 ,,,其中 是 的平方,故不符合题意;
D. 被开方数的因式为 ,指数是 ,故不符合题意.
6. C
【解析】A、当 时,, 无意义,故本选项错误;
B、当 时, 无意义,故本选项错误;
C、因为 ,
所以 符合二次根式的定义;故本选项正确;
D、当 时,, 无意义;故本选项错误.
7. D
8. B
【解析】A., 和 不是同类二次根式,故本选项不符合题意;
B., 和 是同类二次根式,故本选项符合题意;
C., 和 不是同类二次根式,故本选项不符合题意;
D. 和 不是同类二次根式,故本选项不符合题意.
9. C
10. B
二
11.
【解析】 最简二次根式 与 的被开方数相同,
,解得 .
12.
13. ,且
【解析】由题意得:,且 ,
解得:,且 .
14.
【解析】.
15.
16.
【解析】
故答案为:.
三
17. ()()()是最简二次根式,()()()()()都不是最简二次根式.
() 的被开方数不是整数;
() 的被开方数含有分母;
() 的被开方数含有分母;
() 的被开方数含有能开得尽方的因式 ;
() 的被开方数含有能开得尽方的因数 .
故()()()()()都不是最简二次根式.
18. (1) ,含有二次根号且被开方数 为非负数,满足二次根式定义,是二次根式;
(2) ,被开方数 为负数,不满足二次根式定义,不是二次根式;
(3) ,含有二次根号且被开方数 为非负数,满足二次根式定义,是二次根式;
(4) ,没有二次根式,不满足二次根式定义,不是二次根式;
(5) ,当 ,即 时,被开方数为负数,题目中没有标明 的取值范围,因此不满足二次根式定义,不是二次根式;
(6) ,因为 ,所以 ,含有二次根式且被开方数 为非负数,满足二次根式定义,是二次根式;
(7) ,含有二次根号且被开方数 为非负数,满足二次根式定义,是二次根式(对式子本身判断,不需要化简计算);
(8) (, 异号),因为 , 异号,所以 ,被开方数 为负数,不满足二次根式定义,不是二次根式.
19. 由题意,得 ,解得 .
20. .
21. .
22. (1) .
(2) .
(3) .
23. (1) .
(2) .
(3) .
(4) .
24. (1) .
(2) .
25.
当 时,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版2022-20203年八年级(下)第十六章二次根式检测试卷A
(时间120分钟,满分120分)
一、选择题(共10小题;每小题3分,共30分)
1. 下列运算,结果正确的是
A. B. C. D.
2. 若 成立,则 的取值范围为
A. B. C. D. 或
3. 下列二次根式中, 的同类二次根式是
A. B. C. D.
4. 下列判断正确的是
A.
B. 若 ,则
C.
D. 可以表示边长为 的等边三角形的周长
5. 下列二次根式的被开方数中,各因式指数为 的有
A. B. C. D.
6. 下列式子一定是二次根式的是
A. B. C. D.
7. 若三角形的三边长分别是 ,,,且 ,则这个三角形的周长是
A. B. C. D.
8. 在下列各组根式中,是同类二次根式的是
A. 和 B. 和
C. 和 D. 和
9. 按如图所示的程序计算,若开始输入的 值为 ,则最后输出的结果是
A. B. C. D.
10. 若 ,,则下列等式成立的是
A. B. C. D.
二、填空题(共6小题;每小题3分,共18分)
11. 若最简二次根式 与 的被开方数相同,则 .
12. ,则 的取值范围是 .
13. 代数式 在实数范围内有意义,则 的取值范围是 .
14. 计算 的结果是 .
15. .
16. 计算: .
三、解答题(共9小题;共72分)
17.(8分) 下列二次根式中哪些是最简二次根式 哪些不是 若不是,请说明理由.
();();();
();();();
();().
18. (8分)判断下列各式是不是二次根式.
(1);
(2);
(3);
(4);
(5);
(6);
(7);
(8)(, 异号)
19.(8分) 若最简二次根式 与 是同类二次根式,求 的值.
20. (8分)计算:.
21. (8分)计算:.
22. (8分)计算:
(1).
(2).
(3).
23. (8分)计算:
(1);
(2);
(3);
(4).(结果表示为含幂的形式)
24.(8分) 如图,已知正方形 的面积为 ,正方形 的面积为 .
(1)求矩形 的周长;
(2)求矩形 的面积.
25.(8分) 先化简,再求值:,其中 .
答案
一
1. D
【解析】A. 与 不是同类二次根式,不能合并,此选项错误;
B. 与 不是同类二次根式,不能合并,此选项错误;
C.,此选项错误;
D.,此选项计算正确;
故选:D.
2. B
3. D
【解析】.
4. D
【解析】A.,
,
,故本选项错误;
B.若 ,则 或 ,故本选项错误;
C.当 , 时, 成立,故本选项错误.
5. A
【解析】A. 的被开方数的因式指数为 ,故符合题意;
B. 的被开方数的因式分别为 ,,,其中 的指数为 ,故不符合题意;
C. 的被开方数的因式有 ,,,其中 是 的平方,故不符合题意;
D. 被开方数的因式为 ,指数是 ,故不符合题意.
6. C
【解析】A、当 时,, 无意义,故本选项错误;
B、当 时, 无意义,故本选项错误;
C、因为 ,
所以 符合二次根式的定义;故本选项正确;
D、当 时,, 无意义;故本选项错误.
7. D
8. B
【解析】A., 和 不是同类二次根式,故本选项不符合题意;
B., 和 是同类二次根式,故本选项符合题意;
C., 和 不是同类二次根式,故本选项不符合题意;
D. 和 不是同类二次根式,故本选项不符合题意.
9. C
10. B
二
11.
【解析】 最简二次根式 与 的被开方数相同,
,解得 .
12.
13. ,且
【解析】由题意得:,且 ,
解得:,且 .
14.
【解析】.
15.
16.
【解析】
故答案为:.
三
17. ()()()是最简二次根式,()()()()()都不是最简二次根式.
() 的被开方数不是整数;
() 的被开方数含有分母;
() 的被开方数含有分母;
() 的被开方数含有能开得尽方的因式 ;
() 的被开方数含有能开得尽方的因数 .
故()()()()()都不是最简二次根式.
18. (1) ,含有二次根号且被开方数 为非负数,满足二次根式定义,是二次根式;
(2) ,被开方数 为负数,不满足二次根式定义,不是二次根式;
(3) ,含有二次根号且被开方数 为非负数,满足二次根式定义,是二次根式;
(4) ,没有二次根式,不满足二次根式定义,不是二次根式;
(5) ,当 ,即 时,被开方数为负数,题目中没有标明 的取值范围,因此不满足二次根式定义,不是二次根式;
(6) ,因为 ,所以 ,含有二次根式且被开方数 为非负数,满足二次根式定义,是二次根式;
(7) ,含有二次根号且被开方数 为非负数,满足二次根式定义,是二次根式(对式子本身判断,不需要化简计算);
(8) (, 异号),因为 , 异号,所以 ,被开方数 为负数,不满足二次根式定义,不是二次根式.
19. 由题意,得 ,解得 .
20. .
21. .
22. (1) .
(2) .
(3) .
23. (1) .
(2) .
(3) .
(4) .
24. (1) .
(2) .
25.
当 时,
.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
