题型一 选择题(二)-(2023专用)2022年全国小升初真题题型汇编专项训练(人教版,含答案及解析)
文档属性
| 名称 | 题型一 选择题(二)-(2023专用)2022年全国小升初真题题型汇编专项训练(人教版,含答案及解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 14:34:39 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
题型一 选择题(二)-(2023专用)2022年全国小升初
真题题型汇编专项训练(人教版)
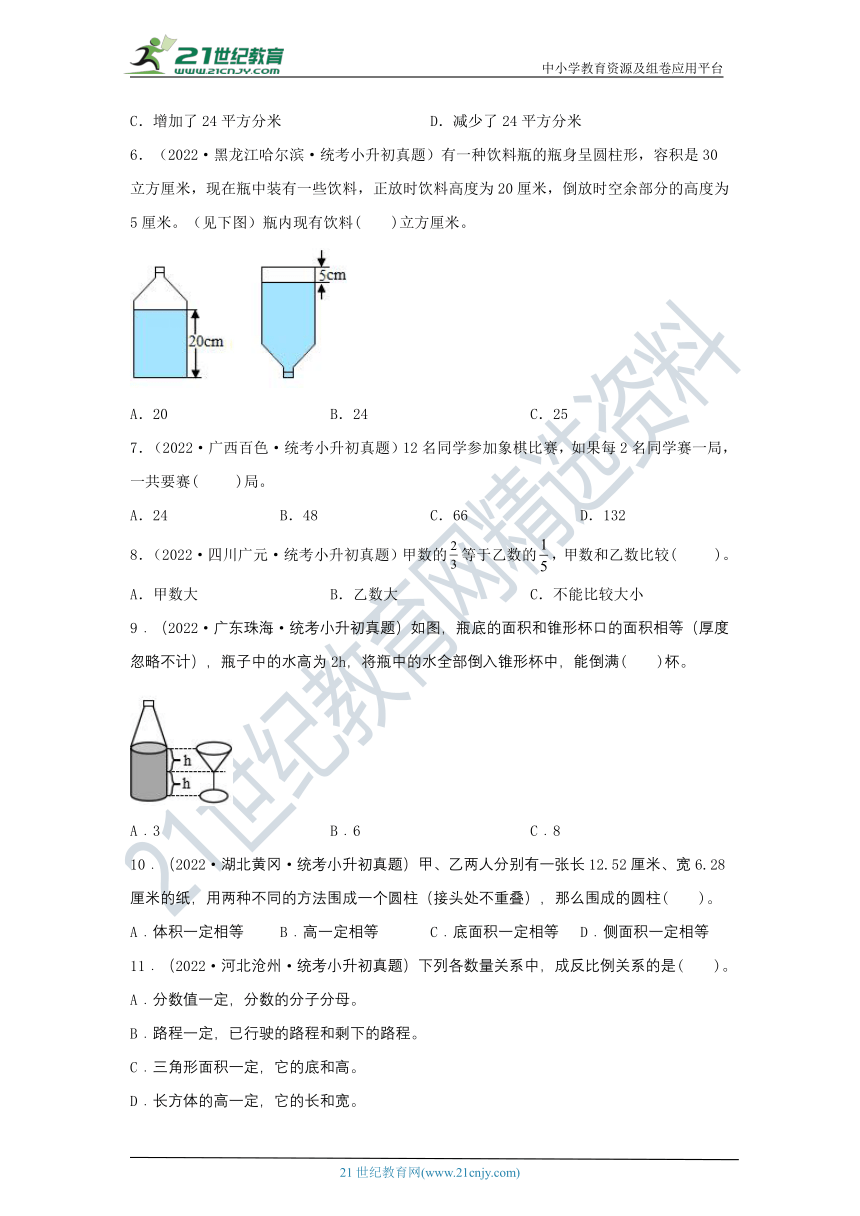
1.(2022·北京海淀·统考小升初真题)下图是六(1)班的教室平面图,亮亮在平面图上量得教室的长为5cm,这间教室的实际长是10m,这幅平面图的比例尺是( )。
A.1∶2 B.2∶1 C.1∶200 D.200∶1
2.(2022·福建泉州·统考小升初真题)长方体体积一定,它的底面积和高( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.(2022·山西晋中·统考小升初真题)制作一个无盖的圆柱形水桶,图中的几种铁皮,可以正好搭配的是( )。
A.①和④ B.①和③ C.②和③
4.(2022·广东珠海·统考小升初真题)实验小学的操场长108米,宽72米,在练习本上画平面图,比较合适的比例尺是( )。
A.1∶200 B.1∶2000 C.1∶20000
5.(2022·贵州铜仁·统考小升初真题)把一个高6分米,底面半径2分米的圆柱切成若干等份,拼成一个近似的长方体(如图)。这时表面积( )。
A.不变 B.增加了12平方分米
C.增加了24平方分米 D.减少了24平方分米
6.(2022·黑龙江哈尔滨·统考小升初真题)有一种饮料瓶的瓶身呈圆柱形,容积是30立方厘米,现在瓶中装有一些饮料,正放时饮料高度为20厘米,倒放时空余部分的高度为5厘米。(见下图)瓶内现有饮料( )立方厘米。
A.20 B.24 C.25
7.(2022·广西百色·统考小升初真题)12名同学参加象棋比赛,如果每2名同学赛一局,一共要赛( )局。
A.24 B.48 C.66 D.132
8.(2022·四川广元·统考小升初真题)甲数的等于乙数的,甲数和乙数比较( )。
A.甲数大 B.乙数大 C.不能比较大小
9.(2022·广东珠海·统考小升初真题)如图,瓶底的面积和锥形杯口的面积相等(厚度忽略不计),瓶子中的水高为2h,将瓶中的水全部倒入锥形杯中,能倒满( )杯。
A.3 B.6 C.8
10.(2022·湖北黄冈·统考小升初真题)甲、乙两人分别有一张长12.52厘米、宽6.28厘米的纸,用两种不同的方法围成一个圆柱(接头处不重叠),那么围成的圆柱( )。
A.体积一定相等 B.高一定相等 C.底面积一定相等 D.侧面积一定相等
11.(2022·河北沧州·统考小升初真题)下列各数量关系中,成反比例关系的是( )。
A.分数值一定,分数的分子分母。
B.路程一定,已行驶的路程和剩下的路程。
C.三角形面积一定,它的底和高。
D.长方体的高一定,它的长和宽。
12.(2022·云南昭通·统考小升初真题)小明家住在8楼,他家的车位在﹣2楼,如果乘坐电梯每上一层楼需要3秒(电梯中途不停),那么他从﹣2楼乘坐电梯到8楼需要( )秒。www.21-cn-jy.com
A.27 B.30 C.24 D.33
13.(2022·江西赣州·统考小升初真题)圆柱、圆锥、正方体和长方体的底面周长和高相等,( )的体积最大。
A.圆柱 B.圆锥 C.正方体 D.长方体
14.(2022·广西百色·统考小升初真题)欢欢班里同学的平均身高是,乐乐班里同学的平均身高是,那么欢欢和乐乐比,( )。
A.欢欢高 B.乐乐高 C.一样高 D.无法确定谁高
15.(2022·北京顺义·统考小升初真题)妈妈榨了一大杯橙汁招待客人,倒入小杯子中(如图),可以倒满( )杯。
A.3 B.6 C.9 D.15
16.(2022·湖南邵阳·统考小升初真题)下面各项中两种量成正比例关系的是( )。
A.路程一定,速度和时间
B.长方形的周长一定,长和宽
C.直径一定,圆周率和圆的周长
D.圆柱的高一定,体积和底面积
17.(2022·山西阳泉·统考小升初真题)下题中的两种量,成反比例关系的是( )。
A.爸爸比小红大25岁,爸爸的年龄和小红的年龄
B.商品的折扣一定,原价和现价
C.汽车行驶的路程一定,速度和所用时间
18.(2022·广东广州·统考小升初真题)如图,将圆柱形玻璃杯的水倒入下面编号为( )号圆锥形容器里,正好倒满(单位:厘米)。
A. B. C. D.
19.(2022·浙江宁波·统考小升初真题)一种精密零件长5毫米,把它画在图纸上,量得零件长6厘米,这张图纸的比例尺是( )。
A.5∶6 B.6∶5 C.12∶1 D.1∶12
20.(2022·河南省直辖县级单位·统考小升初真题)下列表述中,成反比例关系的是( )。
A.三角形的高不变,它的底和面积 B.平行四边形的面积一定,它的底和高
C.圆的面积是24m2,它的半径与圆周率 D.你的年龄一定,你的身高与体重
21.(2022·云南昆明·统考小升初真题)云南省体育有中考从七年级开始了,一分钟跳小绳,以每分钟160个为达标。如果将达标成绩记作0,东东的成须应记作-5,则他小绳个数是( )。【来源:21·世纪·教育·网】
A.-5 B.165 C.155 D.无法确定
22.(2022·云南昆明·统考小升初真题)下面能组成比例的两个比是( )。
A.0.9∶3和 B.∶4和1.2∶3.6 C.∶4和5∶ D.和
23.(2022·新疆吐鲁番·统考小升初真题)一个圆柱体,它的侧面展开图是正方形,底面半径是2厘米,它的高是( )。
A.6.28厘米 B.9.42厘米 C.12.56厘米 D.15.7厘米
24.(2022·山东菏泽·统考小升初真题)左边的图形按1∶2缩小后得到的是图形( )。
A.① B.② C.③
25.(2022·河南漯河·统考小升初真题)星光文具店一周内的盈亏情况如表:
星期 一 二 三 四 五
盈亏/元 ﹢1500 ﹢1200 ﹣2400 ﹢1800 ﹣2100
这个文具店这周内的总情况是( )。A.盈利 B.亏损 C.不盈不亏
26.(2022·广东珠海·统考小升初真题)把一张长方形纸分别沿长和宽围成不同的圆柱形纸筒(接头处不重盈),那么圆柱A的侧面积( )圆柱B的侧面积。
A.小于 B.等于 C.大于
27.(2022·浙江宁波·统考小升初真题)如果﹢3表示向东走3米,那么﹣3表示向( )走3米。
A.东 B.南 C.西 D.北
28.(2022·浙江宁波·统考小升初真题)两支蜡烛,当第一支燃去,第二支燃去时,两支蜡烛剩下的部分一样长。这两支蜡烛原来长度的比是( )。
A.∶ B.∶ C.(1-)∶(1-) D.(1-)∶(1-)
29.(2022·浙江宁波·统考小升初真题)由于疫情影响,今年五一期间北仑区某景点接待游客约8万人,比去年同期大约减少了2万人,今年比去年同期大约减少了( )。
A.二成 B.二成五 C.七成五 D.八成
30.(2022·四川凉山·统考小升初真题)王阿姨、张阿姨、丁叔叔、李伯伯分别是工程师、军人、教师。李伯伯不是教师,丁叔叔是军人,只有张阿姨和王阿姨职业相同。李伯伯的职业是( )。
A.军人 B.教师 C.工程师 D.无法确定
31.(2022·福建宁德·统考小升初真题)如图,阴影部分的面积相当于甲圆面积的,相当于乙圆面积的,那么,甲、乙两个圆的面积比是( )。
A. B. C. D.
32.(2022·内蒙古呼伦贝尔·统考小升初真题)下面的比中,不能组成比例的是( )。
A.7∶8 和14∶16 B.0.6∶0.2 和3∶1 C.和10∶9 D.0.2∶2.5和40∶50
33.(2022·河南漯河·统考小升初真题)一个圆柱和一个圆锥等底等高,它们的体积之和是12.56立方厘米,这个圆锥的体积是( )立方厘米。
A.6.28 B.3.14 C.9.42
34.(2022·山西太原·校考小升初真题)下面是两位同学对同一个圆柱的两种不同的切分方法(都是平均分成两部分)。甲同学切分后,表面积比原来增加了( );乙同学切分后,表面积比原来增加了( )。
A.2πr2;4rh; B.2rh;πr2 C.πr2;4rh D.4rh;2πr2
35.(2022·黑龙江哈尔滨·统考小升初真题)下面的说法不正确的是( )。
A.2∶3和0.6∶0.9能组成比例。
B.圆柱的侧面积一定,底面周长和高成正比例。
C.如果甲在乙的东偏南30°方向,则乙在甲的西偏北30°方向。
36.(2022·湖南娄底·统考小升初真题)下列和成正比例关系的是( )。
A. B. C.(>0) D.
37.(2022·广西百色·统考小升初真题)设计人员把一个长5mm的零件画在图纸上长为25cm,这幅图纸的比例尺是( )。
A.1∶5 B.5∶1 C.50∶1 D.1∶50
38.(2022·天津北辰·统考小升初真题)下面的说法错误的是( )。
A.最小的质数是2 B.3.2565656…可以简写为
C.没有大于而小于的分数 D.在一段路程里,速度和时间成反比例
39.(2022·河南郑州·统考小升初真题)下面说法错误的是( )。
A.6,4,2和5这四个数能组成比例
B.6个人坐4把椅子,总有一把椅子上至少坐2人
C.一辆变速自行车,前齿轮的齿数为:48,40;后齿轮的齿数为:28,24,20,18,16,14。一共有12种组合。
40.(2022·河南三门峡·统考小升初真题)某小学有6个年级,每个年级有8个班。一天放学,8位小朋友一起走出校门。下列说法中正确的是( )。
A.他们中至少有2人的出生月份相同 B.他们中至少有2人是同一年级的
C.他们中至少有2人的属相相同 D.他们中至少有2人是同一班级的
41.(2022·河北沧州·统考小升初真题)甲数的等于乙数的,甲数∶乙数=( )。
A.6∶5 B.5∶6 C.2∶15 D.15∶2
42.(2022·山西晋中·统考小升初真题)下列说法中正确的有( )。
①今年是闰年,全年共有366天。
②今年的小麦产量比去年增加了一成,也就是今年的小麦产量是去年的110%。
③甲∶乙=4∶5,则乙比甲多25%。
④一个自然数,如果不是质数,就一定是合数。
A.②③ B.①②③ C.②③④
43.(2022·贵州黔西·统考小升初真题)如果12A=5B,那么A∶B=( )。
A.60∶1 B.1∶60 C.12∶5 D.5∶12
44.(2022·甘肃武威·统考小升初真题)一根体积为120立方分米的圆柱体木料,把它削成一个最大的圆锥。圆锥的体积是( )立方分米。21*cnjy*com
A.40 B.60 C.80
45.(2022·福建泉州·统考小升初真题)折扣、成数、税率、利率都是百分数在生活中的应用。下面说法错误的是( )。
A.某商品打七五折出售,就是按原价的75%出售。
B.农业收成,经常用“成数”表示,三成五就是35%。
C.优惠三折表示现价是原价的30%。
D.税率指应纳税额与各种收入中应纳税部分的百分比。
46.(2022·福建泉州·统考小升初真题)甲乙两座城市之间相距210千米,而在一幅地图上,这两地之间距离正好是王老师的一“拃”(手张开后大拇指和中指指尖之间的距离),这幅地图的比例尺可能是( )。
A.1∶10000 B.1∶1000000 C.1∶10000000 D.1000000∶1
47.(2022·甘肃金昌·统考小升初真题)手工课上同学们小组合作制作笔筒。小亮准备了一张长方形的硬纸板作为笔筒的侧面(如图),请联系生活实际思考:下面最适合作为这个笔筒底面的是( )(接头处忽略不计)。
A. B. C.
48.(2022·甘肃天水·统考小升初真题)两个高相等,底面半径之比是的圆柱与圆锥,它们的体积之比是( )
A. B. C. D.
49.(2022·湖南岳阳·统考小升初真题)已知4x=5y,x与y( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
50.(2022·北京顺义·统考小升初真题)一个半径是3厘米、高是12厘米的圆柱形物品,想一想它最有可能是( )。
A.牙签筒 B.铅笔 C.水杯 D.胶棒
51.(2022·内蒙古呼伦贝尔·统考小升初真题)将一个圆柱沿底面直径横向切开后,得到的切面是个宽,面积是的长方形(如图)。原来这个圆柱的体积是( )。
A.188.4 B.282.6 C.360 D.1130.4
52.(2022·湖北孝感·统考小升初真题)一个电子零件的实际长度是3毫米,画在图纸上的长度是6厘米,这张图纸的比例尺是( )。
A.1∶20 B.20∶1 C.1∶2 D.2∶1
53.(2022·青海海南·统考小升初真题)一种零件长0.5毫米,画在图纸上长5厘米,这幅图的比例是( )。
A.1∶10 B.10∶1 C.1∶100 D.100∶1
54.(2022·广东惠州·统考小升初真题)甲数的等于乙数的(甲数、乙数不为),那么甲数与乙数的比是( )。
A. B. C. D.
55.(2022·天津北辰·统考小升初真题)已知一个比例两个内项的积是30,则两个外项不可能是( )。
A.30和1 B.15和5 C.1.5和20 D.0.75和40
56.(2022·山东济宁·统考小升初真题)把一根长2米的圆柱形木料截成3个小圆柱,3个小圆柱的表面积之和比原来增加了0.6平方米,原来这根木料的体积是( )立方米。
A.1.2 B.0.4 C.0.3 D.0.2512
57.(2022·内蒙古呼伦贝尔·统考小升初真题)关于“0”的说法错误的是( )。
A.0乘任何数都等于0
B.0和正整数都是自然数
C.0能做乘数、减数和除数
D.0既不是正数也不是负数
58.(2022·北京西城·统考小升初真题)通常规定海平面的海拔高度为0m,珠穆朗玛峰高出海平面8848.86m,其海拔高度记作﹢8848.86m,吐鲁番盆地的最低处低于海平面154.31m,其海拔高度记作( )m。
A.﹢154.31 B.﹣154.31 C.﹢8694.55 D.﹣8694.55
59.(2022·辽宁鞍山·统考小升初真题)如图,一个圆锥体酒杯,倒入一些红酒,红酒深为圆锥高的一半,满杯红酒的体积是现在杯中红酒体积的( )倍。
A.2 B.3 C.4 D.8
60.(2022·吉林四平·统考小升初真题)20个孩子参加6个兴趣小组,至少有一个兴趣小组的人不少于( )人。
A.4 B.3 C.5 D.6
61.(2022·山东菏泽·统考小升初真题)利息的计算公式是( )。
A.利息=本金×利率 B.利息=本金×存期 C.利息=本金×利率×存期
62.(2022·黑龙江鸡西·校联考小升初真题)下面( )图形是圆柱的展开图。
A. B.C.
63.(2022·山东菏泽·统考小升初真题)直线上,0在﹣的( )边。
A.左 B.右 C.无法确定
64.(2022·河南三门峡·统考小升初真题)一个圆锥的底面半径扩大到原来的3倍,高缩小到原来的,它的体积扩大到原来的( )倍。
A.6 B.12 C.4.5 D.9
65.(2022·云南昭通·统考小升初真题)圆柱的底面半径和高都扩大到原来的2倍,它的体积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
66.(2022·北京海淀·统考小升初真题)在下面四个空容器中,分别注入60毫升的水(水均不溢出容器,容器壁百度忽略不计)。容器底面尺寸如下图所示(单位:cm),水位最高的是( )。
A. B. C. D.
参考答案及解析部分
1.C
【思路引导】根据比例尺=图上距离∶实际距离,代入数据,化简比即可;注意单位的换算:1m=100cm。21·cn·jy·com
【完整解答】5cm∶10m
=5cm∶(10×100)cm
=5∶1000
=(5÷5)∶(1000÷5)
=1∶200
故选:C
【考察注意点】掌握图上距离、实际距离、比例尺三者之间的关系以及长度单位的换算是解题的关键。
2.B
【思路引导】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【完整解答】长方体底面积×高=体积(一定),长方体体积一定,它的底面积和高成反比例。
故选:B
【考察注意点】关键是理解正比例和反比例的意义,商一定是正比例关系,乘积一定是反比例关系。
3.C
【思路引导】根据圆柱的侧面的长等于底面的周长,算出③、④两种底面的周长就是所需要的侧面的长,据此可以判断。21·世纪*教育网
【完整解答】3×3.14=9.42(dm)
9.42dm=9.42dm
所以③与②可以搭配。
4×2×3.14
=8×3.14
=25.12(dm)
所以没有与④相匹配的。
故选:C
【考察注意点】此题考查了圆柱的侧面的长与底面周长之间的关系,关键是圆柱侧面的长等于底面的周长。
4.B
【思路引导】根据“操场的长是108米,宽是72米,”把长和宽化成以厘米作单位,即长是10800厘米,宽是7200厘米,再根据比例尺的意义,求出相应的图上距离,即可判断用哪种比例尺比较合适。21教育网
【完整解答】由分析可知,如果用1∶200所求的图上距离太大,如果用选项1∶20000比例尺所求的图上距离太小。
如果用1∶2000的比例尺作图,
图上的长是:10800÷2000=5.4(厘米)
图上的宽是:7200÷2000=3.6(厘米)
所以用选项B的比例尺作图,比较合适。
故选:B
【考察注意点】此题主要考查了比例尺的意义,及选择合适的比例尺作图的方法。
5.C
【思路引导】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体后,体积不变,表面积增加了两个切面的面积,每个切面的长等于圆柱的高,切面的宽等于圆柱的底面半径,根据长方形的面积公式:S=ab,把数据代入公式解答。
【完整解答】6×2×2
=12×2
=24(平方分米)
即表面积增加了24平方分米。
故选:C
【考察注意点】此题考查的目的是理解掌握圆柱体积公式的推导过程,以及圆柱表面积的意义及应用。
6.B
【思路引导】瓶子的形状不规则,并且不知道底面的半径,似乎无法计算。比较一下正放与倒放,因为瓶子的容积不变,装的饮料的体积不变,所以空余部分的体积应当相同。将正放与倒放的空余部分变换一下位置,可以看出饮料瓶的容积应当等于底面积不变,高为20+5=25(厘米)的圆柱的体积,推知饮料占容积的=,所以瓶内现有饮料可求。
【完整解答】30×
=30×
=24(立方厘米)
故选:B
【考察注意点】此题解答关键是理解:左图中20厘米高的饮料以上至瓶口部分的容积相当于右图中上面5厘米高的那部分的容积,进而求出瓶中的饮料的体积占瓶子容积的几分之几,然后用乘法解答即可。
7.C
【思路引导】因为每一名同学都要和其他11名同学比赛,每名同学比赛11局,(局),但每两名同学之间都重复了一次,因此一共要赛(局)。
【完整解答】12×(12-1)÷2
=132÷2
=66(局)
一共要赛66局。
故选:C。
【考察注意点】在循环赛制中,参赛人数和比赛场数的关系为:比赛场数=参赛人数×(参赛人数-1)÷2。
8.B
【思路引导】本题可根据比例的基本性质求出甲、乙两数的比,再根据两个数比的大小来确定甲数和乙数的大小。
【完整解答】甲数×=乙数×
根据比例的基本性质,把甲数和看作比例的两个外项,把乙数和看作比例的两个内项,可得甲数∶乙数=∶=(×15)∶(×15)=3∶10
所以甲数小于乙数。
故选:B
【考察注意点】本题根据等量关系求出甲与乙的比,比较大小就变得比较容易。
9.B
【思路引导】通过观察图形可知,瓶底的面积和锥形杯口的面积相等,瓶子中的水高为2h,圆锥形杯子的高为h,因为等底等高的圆柱的体积是圆锥体积的3倍,所以底面积相等,瓶子中的水高为2h时,圆柱的体积是圆锥体积的(3×2)倍。据此解答。
【完整解答】由分析可知:瓶子中高度为h的水的体积可以倒满3个锥形杯子,
所以将瓶中的水全部倒入锥形杯中,能倒满2×3=6杯。
故选:B
【考察注意点】解答此题的关键是,根据题意,结合等底等高的圆锥形的体积是圆柱形体积的,即可得到答案。
10.D
【思路引导】围成的圆柱有两个:一个是以12.52厘米为高,6.28厘米为底面周长的圆柱;另一个是以6.28厘米为高,12.52厘米为底面周长的圆柱;围成的圆柱的侧面积都等于长12.52厘米,宽6.28厘米的长方形纸面积;据此即可解答问题。
【完整解答】由分析可知:两种方法围成的圆柱的侧面积都等于长方形纸的面积,所以围成的圆柱侧面积一定相等。
故选:D
【考察注意点】解答此题的关键是根据圆柱的围成方法,明确围成的圆柱的底面周长和高的值。
11.C
【思路引导】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【完整解答】A.分子÷分母=分数值(一定),是比值一定,所以分子和分母成正比例;
B.已行的路程+剩下的路程=全程(一定),即和一定,所以已行驶的路程和剩下的路程不成比例;
C.因为三角形的面积=底×高÷2,所以:底×高=2×三角形的面积(一定),符合反比例的意义;
D.长方体的高一定,它的长和宽不成比例。
故选:C
【考察注意点】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
12.A
【思路引导】小明从﹣2楼乘坐电梯到8楼需要走(2+8-1)个楼梯间隔,然后乘每上一层楼需要的时间即可求出需要的时间。
【完整解答】3×(2+8-1)
=3×9
=27(秒)
故选:A
【考察注意点】此题的解题关键是掌握植树问题中的处理方法,主要用到的知识点:楼梯间隔数=层数-1。
13.A
【思路引导】周长相等的长方形、正方形、圆形中,圆的面积最大;因为圆柱、圆锥、正方体和长方体的底面周长相等,高相等,而圆柱体的底面积最大,根据圆柱、圆锥、正方体和长方体的体积=底面积×高,可采用举例进行证明,由此解答即可。
【完整解答】假设它们的底面周长都是12.56厘米,高都是3.14厘米,
则圆柱体(圆锥体)的底面半径为12.56÷3.14÷2=2厘米,
所以圆柱的体积是3.14×22×3.14=39.4384立方厘米;
圆锥的体积是39.4384×≈13.15(立方厘米);
正方体的棱长为12.56÷4=3.14厘米,
正方体的体积是3.14×3.14×3.14≈30.96立方厘米;
因为12.56÷2=6.28,
所以长方体的长和宽可以是3.15厘米和3.13厘米,
长方体的体积是3.15×3.13×3.14=30.95883立方厘米;
39.4384>30.96>30.95883>13.15,
所以圆柱体的体积最大。
故选:A
【考察注意点】此题主要考查的知识点是:周长相等的长方形、正方形、圆形中,圆的面积最大,其次是正方形的面积,长方形的面积最小;圆柱的体积公式、圆锥的体积公式、正方体的体积公式和长方体的体积公式的应用。
14.D
【思路引导】平均数反映的是一组数据的特征,不是其中某一个数据的特征,欢欢所在班级学生平均身高比乐乐所在班级学生平均身高低,并不代表欢欢的身高就比乐乐低。因此无法确定欢欢和乐乐谁高,据此解答即可。
【完整解答】欢欢和乐乐比,无法确定谁高;
故选:D。
【考察注意点】明确平均数的意义是解答本题的关键。
15.C
【思路引导】根据圆柱体积=底面积×高,圆锥体积=底面积×高÷3,分别求出橙汁体积和小杯子容积,用橙汁体积÷小杯子容积,结果用去尾法保留近似数即可。
【完整解答】8÷2=4(cm)
3.14×42×15÷(3.14×42×5÷3)
=15÷5×3
=9(杯)
故选:C
【考察注意点】关键是掌握并灵活运用圆柱和圆锥的体积公式。
16.D
【思路引导】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【完整解答】A.时间×速度=路程(一定),符合反比例的意义;
B.长方形的周长=2×(长+宽),长+宽=周长(一定),所以不成比例关系;
C.圆的周长=,周长÷=直径(不是一定的值),所以不成比例关系;
D.体积÷底面积=高(一定),符合正比例的意义。
故选:D
【考察注意点】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再判断即可。21cnjy.com
17.C
【思路引导】乘积一定的两个量成反比例关系,商一定的两个量成正比例关系。据此分析,找出选项中成反比例关系的即可。
【完整解答】A.爸爸年龄-小红年龄=25岁,爸爸的年龄和小红的年龄不成比例关系;
B.现价÷原价=折扣(一定),所以原价和现价成正比例关系;
C.速度×时间=路程(一定),所以速度和所用时间成反比例关系。
故选:C
【考察注意点】本题考查了正比例和反比例,掌握二者的定义是解题的关键。
18.C
【思路引导】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,计算出水的体积和每个圆锥的容积即可做出选择。
【完整解答】3.14×(10÷2)2×6
=3.14×25×6
=471(立方厘米)
A.3.14×(12÷2)2×18×
=3.14×36×18×
=113.04×18×
=678.24(立方厘米)
B.3.14×(10÷2)2×16×
=3.14×25×16×
=78.5×16×
≈418.6(立方厘米)
C.3.14×(10÷2)2×18×
=3.14×25×18×
=78.5×18×
=471(立方厘米)
D.3.14×(10÷2)2×6×
=3.14×25×6×
=78.5×6×
=157(立方厘米)
故选:C
【考察注意点】此题考查了圆柱、圆锥的体积计算,掌握公式认真解答即可。
19.C
【思路引导】根据图上距离∶实际距离=比例尺,写出图上与实际距离的比,化简即可。
【完整解答】6厘米∶5毫米=60毫米∶5毫米=12∶1
故选:C
【考察注意点】比例尺没有单位名称。为了方便,通常把比例尺的前项化作1(图上距离大于实际距离的,常把后项化为1)。
20.B
【思路引导】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【完整解答】A.三角形的面积×2÷底=高(一定),商一定,所以三角形的底和面积成正比例关系,所以A不符合;
B.平行四边形的底×高=平行四边形的面积(一定),乘积一定,所以它的底和高成反比例,所以B符合;
C.圆周率是一个定值,不是变量,所以圆的半径与圆周率不成比例,所以C不符合;
D.一个人的身高和年龄不成比例,通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高,所以D不符合。
故选:B
【考察注意点】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
21.C
【思路引导】题意可知,以每分钟160个为达标,记作0,超过160记为正,低于160记为负,所以-5表示这个学生可以做160-5=155(个)。
【完整解答】160- 5=155(个)
故选:C
【考察注意点】本题考查了负数的意义,找准标准是关键。
22.D
【思路引导】判断四个数能否组成比例,可根据比例的性质,看看这四个数中是不是存在其中两个数的积等于另外两个数的积,若是,则成比例,若不是,则不成比例;据此解答。
【完整解答】A.因为3×≠×0.9,所以不能组成比例;
B.因为1.2×4≠×3.6,所以不能组成比例;
C.因为4×5≠×,所以不能组成比例;
D.因为×=1×,所以能组成比例。
故选:D
【考察注意点】解决此题也可以根据比例的意义,先逐项求出每个比的比值,进而根据两个比的比值相等,就能组成比例,比值不相等,就不能组成比例。
23.C
【思路引导】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开后是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,当圆柱的侧面展开图是正方形时,这个圆柱的底面周长和高相等。根据圆的周长公式:C=2πr,把数据代入公式解答。
【完整解答】2×3.14×2
=6.28×2
=12.56(厘米)
故选:C
【考察注意点】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆的周长公式及应用,关键是熟记公式。
24.A
【思路引导】把图形按1∶2缩小,则图形的宽和高都缩小到原来的,据此判断即可。
【完整解答】图形①是将宽和高都缩小到原来的,与原图形状相同,只是大小不同,所以图形①是原图按1∶2缩小后得到的图形;
图形②是将高缩小到原来的,宽没变,与原图的形状不相同,所以这个图形是错误的;
图形③是将宽缩小到原来的,高没变,与原图的形状不相同,所以这个图形是错误的。
故选:A
【考察注意点】本题主要考查图形的放大和缩小,要注意每条边都需要按一定的比例放大或者缩小,图形不变。
25.C
【思路引导】正数、负数表示两种相反意义的量;从表格中可以看出,盈利记为正,亏损记为负;先分别计算出盈利、亏损的总金额,再比较大小,如果盈利的金额大于亏损的金额,那么这个文具店这周内的总情况是盈利的,反之为亏损。
【完整解答】1500+1200+1800=4500(元)
2400+2100=4500(元)
4500=4500
所以,这个文具店这周内的总情况是不盈不亏。
故选:C
【考察注意点】掌握正负数的意义及应用是解题的关键。
26.B
【思路引导】根据圆柱侧面展开图的特征可知,圆柱的侧面沿高展开是一个长方形。这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。由此可知,A、B两个不同的圆柱形纸筒的侧面积相等,据此解答。
【完整解答】由分析可得:A、B两个不同的圆柱形纸筒的侧面积相等。
故选:B
【考察注意点】此题考查的目的是理解掌握圆柱侧面积的意义及应用。
27.C
【思路引导】用正负数表示意义相反的两种量:向东走记作正,则向西走就记作负。由此得解。
【完整解答】如果﹢3表示向东走3米,那么﹣3表示向西走3米。
故选:C
【考察注意点】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
28.D
【思路引导】把原来的两支蜡烛的长度看作“1”,当第一支燃去,可知剩下的长度是(1-),当第二支燃去时,可知剩下长度是(1-);根据“两支蜡烛剩下的部分一样长”可得出等量关系式:第一支的长度×(1-)=第二支的长度×(1-);然后根据比例的基本性质,把这个等式改写成比的形式即可。
【完整解答】经分析:
第一支的长度×(1-)=第二支的长度×(1-)
即:第一支的长度∶第二支的长度=(1-)∶(1-)
故选:D
【考察注意点】解答此题的关键是先求出第一支和第二支剩下的分率,进行结合题意,根据一个数乘分数的意义写出等式,再把等式改写成比例,化简即可。
29.A
【思路引导】求今年比去年同期大约减少了几成,就是求今年比去年减少的人数占去年人数的百分之几,再化成成数,是把去年接待的人数看成单位“1”,用今年接待的人数加上2万人,求出去年接待的人数,再用2万人除以去年接待的人数即可求解。
【完整解答】2÷(8+2)×100%
=2÷10×100%
=20%
20%=二成
故选:A
【考察注意点】本题是求一个数是另一个数的百分之几,关键是看把谁当成了单位“1”,单位“1”的量为除数;同时考查了成数的含义。
30.C
【思路引导】王阿姨、张阿姨、丁叔叔、李伯伯分别是工程师、军人、教师,只有张阿姨和王阿姨职业相同,丁叔叔是军人,说明李伯伯不是军人,李伯伯也不是教师,则李伯伯是工程师。
【完整解答】李伯伯不是军人,李伯伯也不是教师,则李伯伯是工程师。
故选:C
【考察注意点】本题考查数学思考,解答本题的关键是找到题中的关键信息。
31.B
【思路引导】根据题意可知,甲圆面积×=乙圆面积×,根据比例的基本性质可知,甲圆面积∶乙圆面积=∶=5∶4,据此解答即可。21*cnjy*com
【完整解答】阴影部分的面积相当于甲圆面积的,相当于乙圆面积的,那么,甲、乙两个圆的面积比是5∶4;
故选:B。
【考察注意点】本题综合性较强,熟练掌握分数乘法的意义、灵活利用比例的基本性质是解答本题的关键。
32.D
【思路引导】根据比例的基本性质,看选项中的内项积是否等于外项积来进行判断。
【完整解答】A.7×16=8×14,能组成比例;
B.0.6×1=0.2×3,能组成比例;
C.×9=×10,能组成比例;
D.0.2×50≠2.5×40,不能组成比例;
故选:D
【考察注意点】掌握比例的基本性质:内项积等于外项积。
33.B
【思路引导】根据等底等高的圆柱是圆锥体积的3倍可知,圆锥的体积是1份,圆柱的体积是3份,由“它们的体积一共是12.56立方厘米”,则12.56立方厘米就是4份的体积之和,求出1份就是圆锥的体积。
【完整解答】根据题意,把圆锥的体积是1份,圆柱的体积是3份,可得:
1+3=4
12.56÷4=3.14(立方厘米)
所以,圆锥的体积是3.14立方厘米。
故选:B
【考察注意点】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
34.A
【思路引导】由题意分析可得,甲同学切分后,表面积增加了两个底面的圆的面积,根据圆的面积公式可得增加了πr2×2=2πr2,乙同学切分后,表面积增加了两个长为2r,宽为h的长方形,所以增加了2r×h×2=4rh。据此解答。
【完整解答】甲同学切分后,表面积比原来增加了2πr2,乙同学切分后,表面积比原来增加了4rh。
故选:A
【考察注意点】本题主要考查了圆柱的切拼,注意圆柱切的方向。
35.B
【思路引导】(1)根据比例的意义:表示两个比相等的式子,分别化简每一组比,再看它们的比值是否相等即可;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,即可解答;
(3)根据位置的相对性可知,它们的方向相反,角度相等,据此解答。
【完整解答】A.2∶3=,0.6∶0.9=,比值相等,2∶3和0.6∶0.9能组成比例,原题说法正确;
B.圆柱的底面周长×高=侧面积(一定),乘积一定,所以它的底面周长和高成反比例,原题说法错误;
C.如果甲在乙的东偏南30°方向,则乙在甲的西偏北30°方向,原题的说法正确。
故选:B
【考察注意点】判断成正反比例是本题的一个难点,需要熟悉其中的数量关系,以及正反比例的辨识方法。
36.B
【思路引导】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例;如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。【出处:21教育名师】
【完整解答】A.,和一定,与不成比例;
B.,则,比值一定,与成正比例关系;
C.,则,乘积一定,与成反比例关系;
D.,差一定,与不成比例。
故选:B
【考察注意点】掌握正、反比例的意义及辨识方法是解题的关键。
37.C
【思路引导】根据图上距离∶实际距离=比例尺,据此解答即可。
【完整解答】5mm=0.5cm
25∶0.5=(25×4)∶(0.5×4)
=100∶2
=(100÷2)∶(2÷2)
=50∶1
故选:C
【考察注意点】本题考查比例尺,明确图上距离∶实际距离=比例尺是解题的关键。
38.C
【思路引导】A.一个数的因数只有1和它本身两个因数,这样的数就是质数,据此判断。
B.循环小数的简便写法,在循环节的首位和末尾的数字上面点上一个点,据此判断。
C.根据分数的基本性质,分子和分母同时乘或除以一个不为0的数,分数的大小不变,据此判断。
D.两个相关联的量,它们的乘积一定,则它们成反比例关系,据此判断。
【完整解答】A.最小的质数是2,原题干说法正确。
B.3.2565656…可以简写为,原题干说法正确。
C.=,=,大于而小于的数有,原题干说法错误。
D.因为速度×时间=路程(一定),它们的乘积一定,所以速度和时间成反比例关系,原题干说法正确。
故选:C
【考察注意点】本题考查正反比例的判定,明确正反比例的定义是解题的关键。
39.A
【思路引导】根据比例的基本性质,把这四个数两两组合,计算乘积,如果有两个数的乘积等于另两个数的乘积,那么这四个数就能组成比例;2·1·c·n·j·y
根据抽屉原理,如果把(n+1)个物体放在n个抽屉里,那么必有一个抽屉中至少放有2个物体;
根据乘法原理可以得到2×6=12种速度组合;据此解答即可。
【完整解答】A.6×2≠4×5,所以6,4,2和5这四个数不能组成比例,说法错误;
B.6÷4=1(个)……2(人),6人中先任意抽4个人分别坐在4个凳子上,另外2个人再坐,只能坐在有人的凳子上。所以,总有一个凳子至少坐2人;说法正确;
C.2×6=12,所以前齿轮的齿数为:48,40;后齿轮的齿数为:28,24,20,18,16,14。一共有12种组合;说法正确。21教育名师原创作品
故选:A
【考察注意点】本题考查了比例的基本性质、抽屉问题、乘法原理,应熟练掌握。
40.B
【思路引导】这个小学总共有48个班级,A选项,总数是8个学生,抽屉数是12个月份;B选项,总数是8个学生,抽屉数是6个年级;C选项,总数是8个学生,抽屉数是12个属相;D选项,总数是8个学生,抽屉数是48个班级。
【完整解答】A.8位小朋友的出生月份可以互不相同,不能保证至少有2人的出生月份相同,错误;
B.,,至少有2人是同一年级的,正确;
C.8位小朋友的属相可以互不相同,不能保证至少有2人的属相相同,错误;
D.8位小朋友的班级可以互不相同,不能保证至少有2人是同一班级的,错误;
故答案选:B。
【考察注意点】本题考查的是抽屉原理,求解问题的关键是确定抽屉数是多少。
41.A
【思路引导】甲数的等于乙数的,根据分数乘法的意义可知:甲数×=乙数×,再逆用比例的基本性质,即可得出甲数与乙数的比,最后化简即可。
【完整解答】甲数×=乙数×,根据比例的基本性质,甲数、乙数、、可以组成比例,
得到甲数∶乙数=∶,化简后甲数∶乙数=6∶5。
故选:A
【考察注意点】本题考查灵活利用比例的基本性质解决问题。
42.A
【思路引导】①判定平年、闰年的方法:普通年份是4的倍数,整百年份是400的倍数,即是闰年;闰年全年366天,平年全年365天;据此判断即可;
②把去年的粮食产量看作单位“1”,今年的粮食产量比去年增加一成,即增加10%,今年的产量是去年产量的(1+10%);据此解答;
③甲∶乙=4∶5,把甲看作4份,乙则有相同的5份,乙比甲多百分之几,以甲作单位“1”,据此用乙比甲多的份数除以甲的份数再乘100%,算出乙比甲多百分之几;
④判断要搞清自然数的分类标准,按质数、合数分,是看一个自然数因数的个数,只有2个因数的是质数,2个以上的是合数;而1是自然数,只有1个因数,所以既不属于质数,也不属于合数,由此判定即可。
【完整解答】①2022÷4=505……2
2022不是4的倍数,所以今年是平年,平年2月只有28天,全年只有365天,所以①说法错误;
②今年的小麦产量比去年增加了一成,把去年小麦产量看作单位“1”,今年小麦产量是去年的1+10%=110%,所以②说法正确;【来源:21cnj*y.co*m】
③甲∶乙=4∶5,把甲看作“4”,乙看作“5”,(5-4)÷4×100%=25%,即乙比甲多25%,所以③说法正确;
④1既不是质数,也不是合数,所以④说法错误。
故选:A
【考察注意点】解答此题时需要灵活运用已学知识,细心分析题中的每一个说法,才能找出正确的选项。
43.D
【思路引导】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
把12A=5B改写成一个外项是A,一个内项是B的比例,则和A相乘的数12就作为比例的另一个外项,和B相乘的数5就作为比例的另一个内项,据此写出比例即可。
【完整解答】因为12A=5B,所以A∶B=5∶12。
故选:D
【考察注意点】解答此题的关键是比例基本性质的逆运用,要注意:相乘的两个数要做外项就都做外项,要做内项就都做内项。
44.A
【思路引导】根据圆柱体积=底面积×高,圆锥体积=×底面积×高,要把圆柱削成一个最大的圆锥,则这个圆锥的体积是圆柱的。据此解答。
【完整解答】120×=40(立方分米)
圆锥的体积是40立方分米。
故选:A
【考察注意点】本题考查了圆柱、圆锥的体积以及它们之间的关系。
45.C
【思路引导】根据折扣、成数、税率、利率知识可知:打几折,就是按照原价的百分之几十出售;农业收成几成就是百分之几十;税率就是应纳税额与各种收入中应纳税部分的百分比,几成解答即可。
【完整解答】A.某商品打七五折出售,就是按原价的75%出售,选项说法正确;
B.农业收成,经常用“成数”表示,三成五就是35%,选项说法正确;
C.优惠三折表示现价是原价的70%,选项说法错误;
D.税率指应纳税额与各种收入中应纳税部分的百分比,选项说法正确;
故选:C
【考察注意点】本题考查了折扣、成数、税率、利率知识,结合题意分析解答即可。
46.B
【思路引导】根据比例尺的意义∶比例尺是图上距离和实际距离的比,代入数据,进行解答即可。
【完整解答】210千米=21000000厘米,一“拃”大约是21厘米,
21∶21000000=1∶1000000
故选:B
【考察注意点】此类题做题的关键是:利用比例尺的意义,代入数据计算即可。
47.B
【思路引导】长方形硬纸板可以围成圆柱的侧面,分两种情况:(1)以长方形的宽为圆柱的底面周长,长方形的长为圆柱的高,这样的笔筒太高,不符合生活实际;(2)以长方形的长为圆柱的底面周长,长方形的宽为圆柱的高,然后根据r=C÷π÷2,求出圆柱的底面半径;据此选择。
【完整解答】情况一:以长方形的12.56cm作为圆柱的底面周长,25.12cm作为圆柱的高时,笔筒太高,不符合生活实际;
情况二:以长方形的25.12cm作为圆柱的底面周长,12.56cm作为圆柱的高时,圆柱的底面半径是:
25.12÷3.14÷2
=8÷2
=4(cm)
故选:B
【考察注意点】掌握圆柱的侧面展开图的特点,结合实际分情况讨论,灵活运用圆的周长公式是解题的关键。
48.B
【思路引导】设它们的高是h,圆柱的底面半径是1,圆锥的底面半径是2,然后根据圆柱的体积公式:V=Sh,圆锥的体积公式:V=Sh,最后用圆柱的体积比上圆锥的体积即可。
【完整解答】π×12×h∶×π×22×h
=πh∶πh
=1∶
=3∶4
故选:B
【考察注意点】本题考查圆柱和圆锥的体积,熟记公式是解题的关键。
49.A
【思路引导】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【完整解答】因为,所以,商一定,所以x与y成正比例关系。
故选:A
【考察注意点】解答本题的关键就看这两个相关联的量是对应的比值一定,还是对应的乘积一定。
50.C
【思路引导】联系生活实际,按一般情况判断各选项物体的半径与高的尺寸,得出结论。
【完整解答】A.牙签筒的半径<3厘米,高<12厘米,不符合题意;
B.铅笔的半径<3厘米,高>12厘米,不符合题意;
C.水杯的半径约是3厘米,高约是12厘米,符合题意;
D.胶棒的半径<3厘米,高<12厘米,不符合题意。
故选:C
【考察注意点】本题考查圆柱的特征及应用。
51.B
【思路引导】由图可知:切面的长是圆柱的高,宽是圆柱的直径。长方形的面积=长×宽,代入数据求出长方形的长(圆柱的高),再将数据代入圆柱的体积公式计算即可。
【完整解答】60÷6=10(厘米)
3.14×(6÷2)2×10
=3.14×9×10
=3.14×90
=282.6(立方厘米)
故选:B
【考察注意点】本题主要考查立体图形的切拼,明确切面的长是圆柱的高,宽是圆柱的直径是解题的关键。
52.B
【思路引导】比例尺等于图上距离比实际距离,据此先统一单位再做比即可。
【完整解答】6厘米=60毫米,
60∶3=20∶1。
故选:B
【考察注意点】本题考查了比例尺,在求比例尺时,一定要注意先统一单位,避免计算错误。
53.D
【思路引导】图上距离与实际距离的比即为比例尺,实际距离和图上距离已知,代入公式即可求出比例尺。
【完整解答】5厘米=50毫米,
50∶0.5=100∶1;
则这幅图的比例尺是100∶1。
故选:D。
【考察注意点】解答此题的关键是,先统一单位,再代入求比例尺的公式即可。
54.C
【思路引导】由题意可知:甲数乙数,再逆运用比例的基本性质,即两内项之积等于两外项之积,即可求出二者的比。21世纪教育网版权所有
【完整解答】甲数乙数,甲数∶乙数。
故选:C
【考察注意点】此题主要依据比例的基本性质解决问题。
55.B
【思路引导】根据比例的基本性质可知,两个内项的积等于两个外项的积。已知两个内项的积是30,计算四个选项里的乘积,找出结果不是30的选项即可。【版权所有:21教育】
【完整解答】A.30×1=30,30=30;所以这两个外项是可能的;
B.15×5=75,7530;所以这两个外项是不可能的;
C.1.5×20=30,30=30;所以这两个外项是可能的;
D.0.75×40=30,30=30;所以这两个外项是可能的。
故选:B
【考察注意点】此题的解题关键是灵活运用比例的基本性质来求解。
56.C
【思路引导】把圆柱形木料截成3个小圆柱,表面积增加了4个底面的面积,其中一个底面的面积=增加的表面积÷4;原来这根木料的体积=底面积×高。
【完整解答】0.6÷4×2
=0.15×2
=0.3(立方米)
故选:C
【考察注意点】抓住圆柱的切割特点和增加的表面积,先求出圆柱的底面积是解决此类问题的关键。
57.C
【思路引导】根据0的意义,比如相同两个数相减的结果是0;一个数与0相加的和是它本身;一个数减0的差是它本身;0除以任何一个不为0的数商是0;0与任何数相乘的积是0。一个非0的数除以0无意义;0既不是正数也不是负数;逐一判断,可得答案。
【完整解答】A.0乘任何数都等于0表述正确;
B.0和正整数都是自然数表述正确;
C.0能做乘数、减数和除数表述错误,不能做除数;
D.0既不是正数也不是负数表述正确。
故选:C
【考察注意点】此题考查了负数的意义、整数的认识、自然数的认识和乘除法的意义等。
58.B
【思路引导】用正负数表示意义相反的两种量:一种记作正,则和它意义相反的就记作负。由此得解。
【完整解答】根据分析可知,
通常规定海平面的海拔高度为0m,珠穆朗玛峰高出海平面8848.86m,其海拔高度记作﹢8848.86m,吐鲁番盆地的最低处低于海平面154.31m,其海拔高度记作﹣154.31m。
故选:B
【考察注意点】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。2-1-c-n-j-y
59.D
【思路引导】根据圆锥的体积公式:V=πr2h,设大圆锥的底面半径为r,高为h,则小圆锥的底面半径为r,高为h,把数据代入公式求出大小圆锥的体积,再根据求一个数是另一个数的几倍,用除法解答。
【完整解答】解:设大圆锥的底面半径为r,高为h,则小圆锥的底面半径为r,高为h;
πr2h÷[π×(r)2×h]
=πr2h÷[π×r2×h]
=πr2h÷[π×r2h]
=8
故选:D
【考察注意点】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
60.A
【思路引导】20个学生参加6个兴趣小组,20÷6=3(人)……2(人),即平均每组有3人,还余2人,根据抽屉原理可知,至少有一个兴趣小组的学生不少于3+1=4(人),据此解答。
【完整解答】20÷6=3(人)……2(人)
3+1=4(人)
故选:A
【考察注意点】在此类抽屉问题中,至少数=物体数除以抽屉数的商+1(有余数的情况下)。
61.C
【思路引导】根据利息的计算公式是:本金×利率×存期,可计算出利息(注意公式中的时间和利率要对应)。
【完整解答】利息的计算公式是:利息=本金×利率×存期。
故选:C
【考察注意点】此题主要考查的是利息的计算公式。
62.A
【思路引导】圆柱的侧面沿高剪开的展开图是一个长方形(或正方形)。这个长方形(或正方形)的长等于圆柱底面的周长,依据圆的周长公式将数值代入计算并选择。
【完整解答】A.圆是直径是3,圆的周长是3.14×3=9.42,底面周长等于侧面展开图的长,所以图A是圆柱的展开图;
B.圆是直径是3,圆的周长是3.14×3=9.42,底面周长不等于侧面展开图的长,所以图B不是圆柱的展开图;www-2-1-cnjy-com
C.圆是直径是3,圆的周长是3.14×3=9.42,底面周长不等于侧面展开图的长,所以图C不是圆柱的展开图。
故选:A
【考察注意点】此题考查圆柱的侧面展开图,要明确:沿高线剪开,圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高。
63.B
【思路引导】数轴上,0在正数的左边,在负数的右边。据此解题。
【完整解答】﹣是负数,所以在直线上,0在﹣的右边。
故选:B
【考察注意点】本题考查了正负数在数轴上的表示,数轴上正数在0的右边,负数在0的左边。
64.C
【思路引导】根据圆锥的体积公式:,现在的底面半径扩大到原来的3倍,高缩小到原来的,即半径=3r,高=h,代入到体积公式中,观察体积的变化情况。
【完整解答】
=
=
÷=4.5
故选:C
【考察注意点】此题的解题关键是灵活运用圆锥的体积公式,找出变化的规律。
65.D
【思路引导】根据圆柱特征,圆柱底面是一个圆,圆的面积公式为:S=r2,圆柱体积公式:V=Sh,由此可得出圆柱体积公式可以表示为:V=r2h,圆柱的底面半径和高都扩大到原来的2倍,根据积的变化规律:两数相乘,其中一个因数乘m或者除以m(0除外),另一个因数乘n或者除以n(0除外),积就乘mn或者除以mn(0除外),据此判断即可。
【完整解答】由分析可得:
因为V=r2h,因数r扩大到原来的2倍,则r2扩大到原来的倍数为:2×2=4,另一个因数h扩大到原来的2倍,则体积扩大的倍数为:
4×2=8
即体积扩大到原来的8倍。
故选:D
【考察注意点】本题考查了圆柱体积公式的应用,以及积的变化规律的应用。
66.C
【思路引导】由于向四个空容器中分别倒入同样多的水,则容器的底面积越小,容器的水位越高,依此计算四个空容器的底面积进行比较即可求解。
【完整解答】5×4=20(cm2)
4×4=16(cm2)
3×4=12(cm2)
(4÷2)2×3.14
=22×3.14
=4×3.14
=12.56(cm2)
20>16>12.56>12
所以容器C的水位最高。
故选:C
【考察注意点】本题考查了长方体的体积和圆柱的容积,关键是灵活运用长方体的体积和圆柱的容积公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
题型一 选择题(二)-(2023专用)2022年全国小升初
真题题型汇编专项训练(人教版)
1.(2022·北京海淀·统考小升初真题)下图是六(1)班的教室平面图,亮亮在平面图上量得教室的长为5cm,这间教室的实际长是10m,这幅平面图的比例尺是( )。
A.1∶2 B.2∶1 C.1∶200 D.200∶1
2.(2022·福建泉州·统考小升初真题)长方体体积一定,它的底面积和高( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
3.(2022·山西晋中·统考小升初真题)制作一个无盖的圆柱形水桶,图中的几种铁皮,可以正好搭配的是( )。
A.①和④ B.①和③ C.②和③
4.(2022·广东珠海·统考小升初真题)实验小学的操场长108米,宽72米,在练习本上画平面图,比较合适的比例尺是( )。
A.1∶200 B.1∶2000 C.1∶20000
5.(2022·贵州铜仁·统考小升初真题)把一个高6分米,底面半径2分米的圆柱切成若干等份,拼成一个近似的长方体(如图)。这时表面积( )。
A.不变 B.增加了12平方分米
C.增加了24平方分米 D.减少了24平方分米
6.(2022·黑龙江哈尔滨·统考小升初真题)有一种饮料瓶的瓶身呈圆柱形,容积是30立方厘米,现在瓶中装有一些饮料,正放时饮料高度为20厘米,倒放时空余部分的高度为5厘米。(见下图)瓶内现有饮料( )立方厘米。
A.20 B.24 C.25
7.(2022·广西百色·统考小升初真题)12名同学参加象棋比赛,如果每2名同学赛一局,一共要赛( )局。
A.24 B.48 C.66 D.132
8.(2022·四川广元·统考小升初真题)甲数的等于乙数的,甲数和乙数比较( )。
A.甲数大 B.乙数大 C.不能比较大小
9.(2022·广东珠海·统考小升初真题)如图,瓶底的面积和锥形杯口的面积相等(厚度忽略不计),瓶子中的水高为2h,将瓶中的水全部倒入锥形杯中,能倒满( )杯。
A.3 B.6 C.8
10.(2022·湖北黄冈·统考小升初真题)甲、乙两人分别有一张长12.52厘米、宽6.28厘米的纸,用两种不同的方法围成一个圆柱(接头处不重叠),那么围成的圆柱( )。
A.体积一定相等 B.高一定相等 C.底面积一定相等 D.侧面积一定相等
11.(2022·河北沧州·统考小升初真题)下列各数量关系中,成反比例关系的是( )。
A.分数值一定,分数的分子分母。
B.路程一定,已行驶的路程和剩下的路程。
C.三角形面积一定,它的底和高。
D.长方体的高一定,它的长和宽。
12.(2022·云南昭通·统考小升初真题)小明家住在8楼,他家的车位在﹣2楼,如果乘坐电梯每上一层楼需要3秒(电梯中途不停),那么他从﹣2楼乘坐电梯到8楼需要( )秒。www.21-cn-jy.com
A.27 B.30 C.24 D.33
13.(2022·江西赣州·统考小升初真题)圆柱、圆锥、正方体和长方体的底面周长和高相等,( )的体积最大。
A.圆柱 B.圆锥 C.正方体 D.长方体
14.(2022·广西百色·统考小升初真题)欢欢班里同学的平均身高是,乐乐班里同学的平均身高是,那么欢欢和乐乐比,( )。
A.欢欢高 B.乐乐高 C.一样高 D.无法确定谁高
15.(2022·北京顺义·统考小升初真题)妈妈榨了一大杯橙汁招待客人,倒入小杯子中(如图),可以倒满( )杯。
A.3 B.6 C.9 D.15
16.(2022·湖南邵阳·统考小升初真题)下面各项中两种量成正比例关系的是( )。
A.路程一定,速度和时间
B.长方形的周长一定,长和宽
C.直径一定,圆周率和圆的周长
D.圆柱的高一定,体积和底面积
17.(2022·山西阳泉·统考小升初真题)下题中的两种量,成反比例关系的是( )。
A.爸爸比小红大25岁,爸爸的年龄和小红的年龄
B.商品的折扣一定,原价和现价
C.汽车行驶的路程一定,速度和所用时间
18.(2022·广东广州·统考小升初真题)如图,将圆柱形玻璃杯的水倒入下面编号为( )号圆锥形容器里,正好倒满(单位:厘米)。
A. B. C. D.
19.(2022·浙江宁波·统考小升初真题)一种精密零件长5毫米,把它画在图纸上,量得零件长6厘米,这张图纸的比例尺是( )。
A.5∶6 B.6∶5 C.12∶1 D.1∶12
20.(2022·河南省直辖县级单位·统考小升初真题)下列表述中,成反比例关系的是( )。
A.三角形的高不变,它的底和面积 B.平行四边形的面积一定,它的底和高
C.圆的面积是24m2,它的半径与圆周率 D.你的年龄一定,你的身高与体重
21.(2022·云南昆明·统考小升初真题)云南省体育有中考从七年级开始了,一分钟跳小绳,以每分钟160个为达标。如果将达标成绩记作0,东东的成须应记作-5,则他小绳个数是( )。【来源:21·世纪·教育·网】
A.-5 B.165 C.155 D.无法确定
22.(2022·云南昆明·统考小升初真题)下面能组成比例的两个比是( )。
A.0.9∶3和 B.∶4和1.2∶3.6 C.∶4和5∶ D.和
23.(2022·新疆吐鲁番·统考小升初真题)一个圆柱体,它的侧面展开图是正方形,底面半径是2厘米,它的高是( )。
A.6.28厘米 B.9.42厘米 C.12.56厘米 D.15.7厘米
24.(2022·山东菏泽·统考小升初真题)左边的图形按1∶2缩小后得到的是图形( )。
A.① B.② C.③
25.(2022·河南漯河·统考小升初真题)星光文具店一周内的盈亏情况如表:
星期 一 二 三 四 五
盈亏/元 ﹢1500 ﹢1200 ﹣2400 ﹢1800 ﹣2100
这个文具店这周内的总情况是( )。A.盈利 B.亏损 C.不盈不亏
26.(2022·广东珠海·统考小升初真题)把一张长方形纸分别沿长和宽围成不同的圆柱形纸筒(接头处不重盈),那么圆柱A的侧面积( )圆柱B的侧面积。
A.小于 B.等于 C.大于
27.(2022·浙江宁波·统考小升初真题)如果﹢3表示向东走3米,那么﹣3表示向( )走3米。
A.东 B.南 C.西 D.北
28.(2022·浙江宁波·统考小升初真题)两支蜡烛,当第一支燃去,第二支燃去时,两支蜡烛剩下的部分一样长。这两支蜡烛原来长度的比是( )。
A.∶ B.∶ C.(1-)∶(1-) D.(1-)∶(1-)
29.(2022·浙江宁波·统考小升初真题)由于疫情影响,今年五一期间北仑区某景点接待游客约8万人,比去年同期大约减少了2万人,今年比去年同期大约减少了( )。
A.二成 B.二成五 C.七成五 D.八成
30.(2022·四川凉山·统考小升初真题)王阿姨、张阿姨、丁叔叔、李伯伯分别是工程师、军人、教师。李伯伯不是教师,丁叔叔是军人,只有张阿姨和王阿姨职业相同。李伯伯的职业是( )。
A.军人 B.教师 C.工程师 D.无法确定
31.(2022·福建宁德·统考小升初真题)如图,阴影部分的面积相当于甲圆面积的,相当于乙圆面积的,那么,甲、乙两个圆的面积比是( )。
A. B. C. D.
32.(2022·内蒙古呼伦贝尔·统考小升初真题)下面的比中,不能组成比例的是( )。
A.7∶8 和14∶16 B.0.6∶0.2 和3∶1 C.和10∶9 D.0.2∶2.5和40∶50
33.(2022·河南漯河·统考小升初真题)一个圆柱和一个圆锥等底等高,它们的体积之和是12.56立方厘米,这个圆锥的体积是( )立方厘米。
A.6.28 B.3.14 C.9.42
34.(2022·山西太原·校考小升初真题)下面是两位同学对同一个圆柱的两种不同的切分方法(都是平均分成两部分)。甲同学切分后,表面积比原来增加了( );乙同学切分后,表面积比原来增加了( )。
A.2πr2;4rh; B.2rh;πr2 C.πr2;4rh D.4rh;2πr2
35.(2022·黑龙江哈尔滨·统考小升初真题)下面的说法不正确的是( )。
A.2∶3和0.6∶0.9能组成比例。
B.圆柱的侧面积一定,底面周长和高成正比例。
C.如果甲在乙的东偏南30°方向,则乙在甲的西偏北30°方向。
36.(2022·湖南娄底·统考小升初真题)下列和成正比例关系的是( )。
A. B. C.(>0) D.
37.(2022·广西百色·统考小升初真题)设计人员把一个长5mm的零件画在图纸上长为25cm,这幅图纸的比例尺是( )。
A.1∶5 B.5∶1 C.50∶1 D.1∶50
38.(2022·天津北辰·统考小升初真题)下面的说法错误的是( )。
A.最小的质数是2 B.3.2565656…可以简写为
C.没有大于而小于的分数 D.在一段路程里,速度和时间成反比例
39.(2022·河南郑州·统考小升初真题)下面说法错误的是( )。
A.6,4,2和5这四个数能组成比例
B.6个人坐4把椅子,总有一把椅子上至少坐2人
C.一辆变速自行车,前齿轮的齿数为:48,40;后齿轮的齿数为:28,24,20,18,16,14。一共有12种组合。
40.(2022·河南三门峡·统考小升初真题)某小学有6个年级,每个年级有8个班。一天放学,8位小朋友一起走出校门。下列说法中正确的是( )。
A.他们中至少有2人的出生月份相同 B.他们中至少有2人是同一年级的
C.他们中至少有2人的属相相同 D.他们中至少有2人是同一班级的
41.(2022·河北沧州·统考小升初真题)甲数的等于乙数的,甲数∶乙数=( )。
A.6∶5 B.5∶6 C.2∶15 D.15∶2
42.(2022·山西晋中·统考小升初真题)下列说法中正确的有( )。
①今年是闰年,全年共有366天。
②今年的小麦产量比去年增加了一成,也就是今年的小麦产量是去年的110%。
③甲∶乙=4∶5,则乙比甲多25%。
④一个自然数,如果不是质数,就一定是合数。
A.②③ B.①②③ C.②③④
43.(2022·贵州黔西·统考小升初真题)如果12A=5B,那么A∶B=( )。
A.60∶1 B.1∶60 C.12∶5 D.5∶12
44.(2022·甘肃武威·统考小升初真题)一根体积为120立方分米的圆柱体木料,把它削成一个最大的圆锥。圆锥的体积是( )立方分米。21*cnjy*com
A.40 B.60 C.80
45.(2022·福建泉州·统考小升初真题)折扣、成数、税率、利率都是百分数在生活中的应用。下面说法错误的是( )。
A.某商品打七五折出售,就是按原价的75%出售。
B.农业收成,经常用“成数”表示,三成五就是35%。
C.优惠三折表示现价是原价的30%。
D.税率指应纳税额与各种收入中应纳税部分的百分比。
46.(2022·福建泉州·统考小升初真题)甲乙两座城市之间相距210千米,而在一幅地图上,这两地之间距离正好是王老师的一“拃”(手张开后大拇指和中指指尖之间的距离),这幅地图的比例尺可能是( )。
A.1∶10000 B.1∶1000000 C.1∶10000000 D.1000000∶1
47.(2022·甘肃金昌·统考小升初真题)手工课上同学们小组合作制作笔筒。小亮准备了一张长方形的硬纸板作为笔筒的侧面(如图),请联系生活实际思考:下面最适合作为这个笔筒底面的是( )(接头处忽略不计)。
A. B. C.
48.(2022·甘肃天水·统考小升初真题)两个高相等,底面半径之比是的圆柱与圆锥,它们的体积之比是( )
A. B. C. D.
49.(2022·湖南岳阳·统考小升初真题)已知4x=5y,x与y( )。
A.成正比例 B.成反比例 C.不成比例 D.无法确定
50.(2022·北京顺义·统考小升初真题)一个半径是3厘米、高是12厘米的圆柱形物品,想一想它最有可能是( )。
A.牙签筒 B.铅笔 C.水杯 D.胶棒
51.(2022·内蒙古呼伦贝尔·统考小升初真题)将一个圆柱沿底面直径横向切开后,得到的切面是个宽,面积是的长方形(如图)。原来这个圆柱的体积是( )。
A.188.4 B.282.6 C.360 D.1130.4
52.(2022·湖北孝感·统考小升初真题)一个电子零件的实际长度是3毫米,画在图纸上的长度是6厘米,这张图纸的比例尺是( )。
A.1∶20 B.20∶1 C.1∶2 D.2∶1
53.(2022·青海海南·统考小升初真题)一种零件长0.5毫米,画在图纸上长5厘米,这幅图的比例是( )。
A.1∶10 B.10∶1 C.1∶100 D.100∶1
54.(2022·广东惠州·统考小升初真题)甲数的等于乙数的(甲数、乙数不为),那么甲数与乙数的比是( )。
A. B. C. D.
55.(2022·天津北辰·统考小升初真题)已知一个比例两个内项的积是30,则两个外项不可能是( )。
A.30和1 B.15和5 C.1.5和20 D.0.75和40
56.(2022·山东济宁·统考小升初真题)把一根长2米的圆柱形木料截成3个小圆柱,3个小圆柱的表面积之和比原来增加了0.6平方米,原来这根木料的体积是( )立方米。
A.1.2 B.0.4 C.0.3 D.0.2512
57.(2022·内蒙古呼伦贝尔·统考小升初真题)关于“0”的说法错误的是( )。
A.0乘任何数都等于0
B.0和正整数都是自然数
C.0能做乘数、减数和除数
D.0既不是正数也不是负数
58.(2022·北京西城·统考小升初真题)通常规定海平面的海拔高度为0m,珠穆朗玛峰高出海平面8848.86m,其海拔高度记作﹢8848.86m,吐鲁番盆地的最低处低于海平面154.31m,其海拔高度记作( )m。
A.﹢154.31 B.﹣154.31 C.﹢8694.55 D.﹣8694.55
59.(2022·辽宁鞍山·统考小升初真题)如图,一个圆锥体酒杯,倒入一些红酒,红酒深为圆锥高的一半,满杯红酒的体积是现在杯中红酒体积的( )倍。
A.2 B.3 C.4 D.8
60.(2022·吉林四平·统考小升初真题)20个孩子参加6个兴趣小组,至少有一个兴趣小组的人不少于( )人。
A.4 B.3 C.5 D.6
61.(2022·山东菏泽·统考小升初真题)利息的计算公式是( )。
A.利息=本金×利率 B.利息=本金×存期 C.利息=本金×利率×存期
62.(2022·黑龙江鸡西·校联考小升初真题)下面( )图形是圆柱的展开图。
A. B.C.
63.(2022·山东菏泽·统考小升初真题)直线上,0在﹣的( )边。
A.左 B.右 C.无法确定
64.(2022·河南三门峡·统考小升初真题)一个圆锥的底面半径扩大到原来的3倍,高缩小到原来的,它的体积扩大到原来的( )倍。
A.6 B.12 C.4.5 D.9
65.(2022·云南昭通·统考小升初真题)圆柱的底面半径和高都扩大到原来的2倍,它的体积扩大到原来的( )倍。
A.2 B.4 C.6 D.8
66.(2022·北京海淀·统考小升初真题)在下面四个空容器中,分别注入60毫升的水(水均不溢出容器,容器壁百度忽略不计)。容器底面尺寸如下图所示(单位:cm),水位最高的是( )。
A. B. C. D.
参考答案及解析部分
1.C
【思路引导】根据比例尺=图上距离∶实际距离,代入数据,化简比即可;注意单位的换算:1m=100cm。21·cn·jy·com
【完整解答】5cm∶10m
=5cm∶(10×100)cm
=5∶1000
=(5÷5)∶(1000÷5)
=1∶200
故选:C
【考察注意点】掌握图上距离、实际距离、比例尺三者之间的关系以及长度单位的换算是解题的关键。
2.B
【思路引导】根据x÷y=k(一定),x和y成正比例关系;xy=k(一定),x和y成反比例关系,进行分析。
【完整解答】长方体底面积×高=体积(一定),长方体体积一定,它的底面积和高成反比例。
故选:B
【考察注意点】关键是理解正比例和反比例的意义,商一定是正比例关系,乘积一定是反比例关系。
3.C
【思路引导】根据圆柱的侧面的长等于底面的周长,算出③、④两种底面的周长就是所需要的侧面的长,据此可以判断。21·世纪*教育网
【完整解答】3×3.14=9.42(dm)
9.42dm=9.42dm
所以③与②可以搭配。
4×2×3.14
=8×3.14
=25.12(dm)
所以没有与④相匹配的。
故选:C
【考察注意点】此题考查了圆柱的侧面的长与底面周长之间的关系,关键是圆柱侧面的长等于底面的周长。
4.B
【思路引导】根据“操场的长是108米,宽是72米,”把长和宽化成以厘米作单位,即长是10800厘米,宽是7200厘米,再根据比例尺的意义,求出相应的图上距离,即可判断用哪种比例尺比较合适。21教育网
【完整解答】由分析可知,如果用1∶200所求的图上距离太大,如果用选项1∶20000比例尺所求的图上距离太小。
如果用1∶2000的比例尺作图,
图上的长是:10800÷2000=5.4(厘米)
图上的宽是:7200÷2000=3.6(厘米)
所以用选项B的比例尺作图,比较合适。
故选:B
【考察注意点】此题主要考查了比例尺的意义,及选择合适的比例尺作图的方法。
5.C
【思路引导】根据圆柱体积公式的推导过程可知,把一个圆柱切拼成一个近似长方体后,体积不变,表面积增加了两个切面的面积,每个切面的长等于圆柱的高,切面的宽等于圆柱的底面半径,根据长方形的面积公式:S=ab,把数据代入公式解答。
【完整解答】6×2×2
=12×2
=24(平方分米)
即表面积增加了24平方分米。
故选:C
【考察注意点】此题考查的目的是理解掌握圆柱体积公式的推导过程,以及圆柱表面积的意义及应用。
6.B
【思路引导】瓶子的形状不规则,并且不知道底面的半径,似乎无法计算。比较一下正放与倒放,因为瓶子的容积不变,装的饮料的体积不变,所以空余部分的体积应当相同。将正放与倒放的空余部分变换一下位置,可以看出饮料瓶的容积应当等于底面积不变,高为20+5=25(厘米)的圆柱的体积,推知饮料占容积的=,所以瓶内现有饮料可求。
【完整解答】30×
=30×
=24(立方厘米)
故选:B
【考察注意点】此题解答关键是理解:左图中20厘米高的饮料以上至瓶口部分的容积相当于右图中上面5厘米高的那部分的容积,进而求出瓶中的饮料的体积占瓶子容积的几分之几,然后用乘法解答即可。
7.C
【思路引导】因为每一名同学都要和其他11名同学比赛,每名同学比赛11局,(局),但每两名同学之间都重复了一次,因此一共要赛(局)。
【完整解答】12×(12-1)÷2
=132÷2
=66(局)
一共要赛66局。
故选:C。
【考察注意点】在循环赛制中,参赛人数和比赛场数的关系为:比赛场数=参赛人数×(参赛人数-1)÷2。
8.B
【思路引导】本题可根据比例的基本性质求出甲、乙两数的比,再根据两个数比的大小来确定甲数和乙数的大小。
【完整解答】甲数×=乙数×
根据比例的基本性质,把甲数和看作比例的两个外项,把乙数和看作比例的两个内项,可得甲数∶乙数=∶=(×15)∶(×15)=3∶10
所以甲数小于乙数。
故选:B
【考察注意点】本题根据等量关系求出甲与乙的比,比较大小就变得比较容易。
9.B
【思路引导】通过观察图形可知,瓶底的面积和锥形杯口的面积相等,瓶子中的水高为2h,圆锥形杯子的高为h,因为等底等高的圆柱的体积是圆锥体积的3倍,所以底面积相等,瓶子中的水高为2h时,圆柱的体积是圆锥体积的(3×2)倍。据此解答。
【完整解答】由分析可知:瓶子中高度为h的水的体积可以倒满3个锥形杯子,
所以将瓶中的水全部倒入锥形杯中,能倒满2×3=6杯。
故选:B
【考察注意点】解答此题的关键是,根据题意,结合等底等高的圆锥形的体积是圆柱形体积的,即可得到答案。
10.D
【思路引导】围成的圆柱有两个:一个是以12.52厘米为高,6.28厘米为底面周长的圆柱;另一个是以6.28厘米为高,12.52厘米为底面周长的圆柱;围成的圆柱的侧面积都等于长12.52厘米,宽6.28厘米的长方形纸面积;据此即可解答问题。
【完整解答】由分析可知:两种方法围成的圆柱的侧面积都等于长方形纸的面积,所以围成的圆柱侧面积一定相等。
故选:D
【考察注意点】解答此题的关键是根据圆柱的围成方法,明确围成的圆柱的底面周长和高的值。
11.C
【思路引导】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。
【完整解答】A.分子÷分母=分数值(一定),是比值一定,所以分子和分母成正比例;
B.已行的路程+剩下的路程=全程(一定),即和一定,所以已行驶的路程和剩下的路程不成比例;
C.因为三角形的面积=底×高÷2,所以:底×高=2×三角形的面积(一定),符合反比例的意义;
D.长方体的高一定,它的长和宽不成比例。
故选:C
【考察注意点】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
12.A
【思路引导】小明从﹣2楼乘坐电梯到8楼需要走(2+8-1)个楼梯间隔,然后乘每上一层楼需要的时间即可求出需要的时间。
【完整解答】3×(2+8-1)
=3×9
=27(秒)
故选:A
【考察注意点】此题的解题关键是掌握植树问题中的处理方法,主要用到的知识点:楼梯间隔数=层数-1。
13.A
【思路引导】周长相等的长方形、正方形、圆形中,圆的面积最大;因为圆柱、圆锥、正方体和长方体的底面周长相等,高相等,而圆柱体的底面积最大,根据圆柱、圆锥、正方体和长方体的体积=底面积×高,可采用举例进行证明,由此解答即可。
【完整解答】假设它们的底面周长都是12.56厘米,高都是3.14厘米,
则圆柱体(圆锥体)的底面半径为12.56÷3.14÷2=2厘米,
所以圆柱的体积是3.14×22×3.14=39.4384立方厘米;
圆锥的体积是39.4384×≈13.15(立方厘米);
正方体的棱长为12.56÷4=3.14厘米,
正方体的体积是3.14×3.14×3.14≈30.96立方厘米;
因为12.56÷2=6.28,
所以长方体的长和宽可以是3.15厘米和3.13厘米,
长方体的体积是3.15×3.13×3.14=30.95883立方厘米;
39.4384>30.96>30.95883>13.15,
所以圆柱体的体积最大。
故选:A
【考察注意点】此题主要考查的知识点是:周长相等的长方形、正方形、圆形中,圆的面积最大,其次是正方形的面积,长方形的面积最小;圆柱的体积公式、圆锥的体积公式、正方体的体积公式和长方体的体积公式的应用。
14.D
【思路引导】平均数反映的是一组数据的特征,不是其中某一个数据的特征,欢欢所在班级学生平均身高比乐乐所在班级学生平均身高低,并不代表欢欢的身高就比乐乐低。因此无法确定欢欢和乐乐谁高,据此解答即可。
【完整解答】欢欢和乐乐比,无法确定谁高;
故选:D。
【考察注意点】明确平均数的意义是解答本题的关键。
15.C
【思路引导】根据圆柱体积=底面积×高,圆锥体积=底面积×高÷3,分别求出橙汁体积和小杯子容积,用橙汁体积÷小杯子容积,结果用去尾法保留近似数即可。
【完整解答】8÷2=4(cm)
3.14×42×15÷(3.14×42×5÷3)
=15÷5×3
=9(杯)
故选:C
【考察注意点】关键是掌握并灵活运用圆柱和圆锥的体积公式。
16.D
【思路引导】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【完整解答】A.时间×速度=路程(一定),符合反比例的意义;
B.长方形的周长=2×(长+宽),长+宽=周长(一定),所以不成比例关系;
C.圆的周长=,周长÷=直径(不是一定的值),所以不成比例关系;
D.体积÷底面积=高(一定),符合正比例的意义。
故选:D
【考察注意点】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再判断即可。21cnjy.com
17.C
【思路引导】乘积一定的两个量成反比例关系,商一定的两个量成正比例关系。据此分析,找出选项中成反比例关系的即可。
【完整解答】A.爸爸年龄-小红年龄=25岁,爸爸的年龄和小红的年龄不成比例关系;
B.现价÷原价=折扣(一定),所以原价和现价成正比例关系;
C.速度×时间=路程(一定),所以速度和所用时间成反比例关系。
故选:C
【考察注意点】本题考查了正比例和反比例,掌握二者的定义是解题的关键。
18.C
【思路引导】圆柱的体积=底面积×高,圆锥的体积=底面积×高×,计算出水的体积和每个圆锥的容积即可做出选择。
【完整解答】3.14×(10÷2)2×6
=3.14×25×6
=471(立方厘米)
A.3.14×(12÷2)2×18×
=3.14×36×18×
=113.04×18×
=678.24(立方厘米)
B.3.14×(10÷2)2×16×
=3.14×25×16×
=78.5×16×
≈418.6(立方厘米)
C.3.14×(10÷2)2×18×
=3.14×25×18×
=78.5×18×
=471(立方厘米)
D.3.14×(10÷2)2×6×
=3.14×25×6×
=78.5×6×
=157(立方厘米)
故选:C
【考察注意点】此题考查了圆柱、圆锥的体积计算,掌握公式认真解答即可。
19.C
【思路引导】根据图上距离∶实际距离=比例尺,写出图上与实际距离的比,化简即可。
【完整解答】6厘米∶5毫米=60毫米∶5毫米=12∶1
故选:C
【考察注意点】比例尺没有单位名称。为了方便,通常把比例尺的前项化作1(图上距离大于实际距离的,常把后项化为1)。
20.B
【思路引导】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定,如果是比值一定,就成正比例,如果是乘积一定,则成反比例。据此解答。
【完整解答】A.三角形的面积×2÷底=高(一定),商一定,所以三角形的底和面积成正比例关系,所以A不符合;
B.平行四边形的底×高=平行四边形的面积(一定),乘积一定,所以它的底和高成反比例,所以B符合;
C.圆周率是一个定值,不是变量,所以圆的半径与圆周率不成比例,所以C不符合;
D.一个人的身高和年龄不成比例,通常在生长期,人的身高是随着年龄的增长而增长,但是生长期过了后,骨膜会闭合,停止长高,所以D不符合。
故选:B
【考察注意点】此题属于辨识成正、反比例的量,就看这两个量是对应的比值一定,还是对应的乘积一定,再作判断。
21.C
【思路引导】题意可知,以每分钟160个为达标,记作0,超过160记为正,低于160记为负,所以-5表示这个学生可以做160-5=155(个)。
【完整解答】160- 5=155(个)
故选:C
【考察注意点】本题考查了负数的意义,找准标准是关键。
22.D
【思路引导】判断四个数能否组成比例,可根据比例的性质,看看这四个数中是不是存在其中两个数的积等于另外两个数的积,若是,则成比例,若不是,则不成比例;据此解答。
【完整解答】A.因为3×≠×0.9,所以不能组成比例;
B.因为1.2×4≠×3.6,所以不能组成比例;
C.因为4×5≠×,所以不能组成比例;
D.因为×=1×,所以能组成比例。
故选:D
【考察注意点】解决此题也可以根据比例的意义,先逐项求出每个比的比值,进而根据两个比的比值相等,就能组成比例,比值不相等,就不能组成比例。
23.C
【思路引导】根据圆柱侧面展开图的特征,圆柱的侧面沿高展开后是一个长方形,这个长方形的长等于圆柱的底面周长,宽等于圆柱的高,当圆柱的侧面展开图是正方形时,这个圆柱的底面周长和高相等。根据圆的周长公式:C=2πr,把数据代入公式解答。
【完整解答】2×3.14×2
=6.28×2
=12.56(厘米)
故选:C
【考察注意点】此题考查的目的是理解掌握圆柱侧面展开图的特征及应用,圆的周长公式及应用,关键是熟记公式。
24.A
【思路引导】把图形按1∶2缩小,则图形的宽和高都缩小到原来的,据此判断即可。
【完整解答】图形①是将宽和高都缩小到原来的,与原图形状相同,只是大小不同,所以图形①是原图按1∶2缩小后得到的图形;
图形②是将高缩小到原来的,宽没变,与原图的形状不相同,所以这个图形是错误的;
图形③是将宽缩小到原来的,高没变,与原图的形状不相同,所以这个图形是错误的。
故选:A
【考察注意点】本题主要考查图形的放大和缩小,要注意每条边都需要按一定的比例放大或者缩小,图形不变。
25.C
【思路引导】正数、负数表示两种相反意义的量;从表格中可以看出,盈利记为正,亏损记为负;先分别计算出盈利、亏损的总金额,再比较大小,如果盈利的金额大于亏损的金额,那么这个文具店这周内的总情况是盈利的,反之为亏损。
【完整解答】1500+1200+1800=4500(元)
2400+2100=4500(元)
4500=4500
所以,这个文具店这周内的总情况是不盈不亏。
故选:C
【考察注意点】掌握正负数的意义及应用是解题的关键。
26.B
【思路引导】根据圆柱侧面展开图的特征可知,圆柱的侧面沿高展开是一个长方形。这个长方形的长等于圆柱的底面周长,宽等于圆柱的高。由此可知,A、B两个不同的圆柱形纸筒的侧面积相等,据此解答。
【完整解答】由分析可得:A、B两个不同的圆柱形纸筒的侧面积相等。
故选:B
【考察注意点】此题考查的目的是理解掌握圆柱侧面积的意义及应用。
27.C
【思路引导】用正负数表示意义相反的两种量:向东走记作正,则向西走就记作负。由此得解。
【完整解答】如果﹢3表示向东走3米,那么﹣3表示向西走3米。
故选:C
【考察注意点】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。
28.D
【思路引导】把原来的两支蜡烛的长度看作“1”,当第一支燃去,可知剩下的长度是(1-),当第二支燃去时,可知剩下长度是(1-);根据“两支蜡烛剩下的部分一样长”可得出等量关系式:第一支的长度×(1-)=第二支的长度×(1-);然后根据比例的基本性质,把这个等式改写成比的形式即可。
【完整解答】经分析:
第一支的长度×(1-)=第二支的长度×(1-)
即:第一支的长度∶第二支的长度=(1-)∶(1-)
故选:D
【考察注意点】解答此题的关键是先求出第一支和第二支剩下的分率,进行结合题意,根据一个数乘分数的意义写出等式,再把等式改写成比例,化简即可。
29.A
【思路引导】求今年比去年同期大约减少了几成,就是求今年比去年减少的人数占去年人数的百分之几,再化成成数,是把去年接待的人数看成单位“1”,用今年接待的人数加上2万人,求出去年接待的人数,再用2万人除以去年接待的人数即可求解。
【完整解答】2÷(8+2)×100%
=2÷10×100%
=20%
20%=二成
故选:A
【考察注意点】本题是求一个数是另一个数的百分之几,关键是看把谁当成了单位“1”,单位“1”的量为除数;同时考查了成数的含义。
30.C
【思路引导】王阿姨、张阿姨、丁叔叔、李伯伯分别是工程师、军人、教师,只有张阿姨和王阿姨职业相同,丁叔叔是军人,说明李伯伯不是军人,李伯伯也不是教师,则李伯伯是工程师。
【完整解答】李伯伯不是军人,李伯伯也不是教师,则李伯伯是工程师。
故选:C
【考察注意点】本题考查数学思考,解答本题的关键是找到题中的关键信息。
31.B
【思路引导】根据题意可知,甲圆面积×=乙圆面积×,根据比例的基本性质可知,甲圆面积∶乙圆面积=∶=5∶4,据此解答即可。21*cnjy*com
【完整解答】阴影部分的面积相当于甲圆面积的,相当于乙圆面积的,那么,甲、乙两个圆的面积比是5∶4;
故选:B。
【考察注意点】本题综合性较强,熟练掌握分数乘法的意义、灵活利用比例的基本性质是解答本题的关键。
32.D
【思路引导】根据比例的基本性质,看选项中的内项积是否等于外项积来进行判断。
【完整解答】A.7×16=8×14,能组成比例;
B.0.6×1=0.2×3,能组成比例;
C.×9=×10,能组成比例;
D.0.2×50≠2.5×40,不能组成比例;
故选:D
【考察注意点】掌握比例的基本性质:内项积等于外项积。
33.B
【思路引导】根据等底等高的圆柱是圆锥体积的3倍可知,圆锥的体积是1份,圆柱的体积是3份,由“它们的体积一共是12.56立方厘米”,则12.56立方厘米就是4份的体积之和,求出1份就是圆锥的体积。
【完整解答】根据题意,把圆锥的体积是1份,圆柱的体积是3份,可得:
1+3=4
12.56÷4=3.14(立方厘米)
所以,圆锥的体积是3.14立方厘米。
故选:B
【考察注意点】此题考查了等底等高的圆柱与圆锥的体积倍数关系的灵活应用。
34.A
【思路引导】由题意分析可得,甲同学切分后,表面积增加了两个底面的圆的面积,根据圆的面积公式可得增加了πr2×2=2πr2,乙同学切分后,表面积增加了两个长为2r,宽为h的长方形,所以增加了2r×h×2=4rh。据此解答。
【完整解答】甲同学切分后,表面积比原来增加了2πr2,乙同学切分后,表面积比原来增加了4rh。
故选:A
【考察注意点】本题主要考查了圆柱的切拼,注意圆柱切的方向。
35.B
【思路引导】(1)根据比例的意义:表示两个比相等的式子,分别化简每一组比,再看它们的比值是否相等即可;
(2)判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例,即可解答;
(3)根据位置的相对性可知,它们的方向相反,角度相等,据此解答。
【完整解答】A.2∶3=,0.6∶0.9=,比值相等,2∶3和0.6∶0.9能组成比例,原题说法正确;
B.圆柱的底面周长×高=侧面积(一定),乘积一定,所以它的底面周长和高成反比例,原题说法错误;
C.如果甲在乙的东偏南30°方向,则乙在甲的西偏北30°方向,原题的说法正确。
故选:B
【考察注意点】判断成正反比例是本题的一个难点,需要熟悉其中的数量关系,以及正反比例的辨识方法。
36.B
【思路引导】判断两种相关联的量之间成什么比例,就看这两个量是对应的比值(商)一定,还是对应的乘积一定;如果是比值(商)一定,这两种相关联的量成正比例;如果是乘积一定,这两种相关联的量成反比例;如果既不是比值一定,也不是乘积一定,则这两种相关联的量不成比例。【出处:21教育名师】
【完整解答】A.,和一定,与不成比例;
B.,则,比值一定,与成正比例关系;
C.,则,乘积一定,与成反比例关系;
D.,差一定,与不成比例。
故选:B
【考察注意点】掌握正、反比例的意义及辨识方法是解题的关键。
37.C
【思路引导】根据图上距离∶实际距离=比例尺,据此解答即可。
【完整解答】5mm=0.5cm
25∶0.5=(25×4)∶(0.5×4)
=100∶2
=(100÷2)∶(2÷2)
=50∶1
故选:C
【考察注意点】本题考查比例尺,明确图上距离∶实际距离=比例尺是解题的关键。
38.C
【思路引导】A.一个数的因数只有1和它本身两个因数,这样的数就是质数,据此判断。
B.循环小数的简便写法,在循环节的首位和末尾的数字上面点上一个点,据此判断。
C.根据分数的基本性质,分子和分母同时乘或除以一个不为0的数,分数的大小不变,据此判断。
D.两个相关联的量,它们的乘积一定,则它们成反比例关系,据此判断。
【完整解答】A.最小的质数是2,原题干说法正确。
B.3.2565656…可以简写为,原题干说法正确。
C.=,=,大于而小于的数有,原题干说法错误。
D.因为速度×时间=路程(一定),它们的乘积一定,所以速度和时间成反比例关系,原题干说法正确。
故选:C
【考察注意点】本题考查正反比例的判定,明确正反比例的定义是解题的关键。
39.A
【思路引导】根据比例的基本性质,把这四个数两两组合,计算乘积,如果有两个数的乘积等于另两个数的乘积,那么这四个数就能组成比例;2·1·c·n·j·y
根据抽屉原理,如果把(n+1)个物体放在n个抽屉里,那么必有一个抽屉中至少放有2个物体;
根据乘法原理可以得到2×6=12种速度组合;据此解答即可。
【完整解答】A.6×2≠4×5,所以6,4,2和5这四个数不能组成比例,说法错误;
B.6÷4=1(个)……2(人),6人中先任意抽4个人分别坐在4个凳子上,另外2个人再坐,只能坐在有人的凳子上。所以,总有一个凳子至少坐2人;说法正确;
C.2×6=12,所以前齿轮的齿数为:48,40;后齿轮的齿数为:28,24,20,18,16,14。一共有12种组合;说法正确。21教育名师原创作品
故选:A
【考察注意点】本题考查了比例的基本性质、抽屉问题、乘法原理,应熟练掌握。
40.B
【思路引导】这个小学总共有48个班级,A选项,总数是8个学生,抽屉数是12个月份;B选项,总数是8个学生,抽屉数是6个年级;C选项,总数是8个学生,抽屉数是12个属相;D选项,总数是8个学生,抽屉数是48个班级。
【完整解答】A.8位小朋友的出生月份可以互不相同,不能保证至少有2人的出生月份相同,错误;
B.,,至少有2人是同一年级的,正确;
C.8位小朋友的属相可以互不相同,不能保证至少有2人的属相相同,错误;
D.8位小朋友的班级可以互不相同,不能保证至少有2人是同一班级的,错误;
故答案选:B。
【考察注意点】本题考查的是抽屉原理,求解问题的关键是确定抽屉数是多少。
41.A
【思路引导】甲数的等于乙数的,根据分数乘法的意义可知:甲数×=乙数×,再逆用比例的基本性质,即可得出甲数与乙数的比,最后化简即可。
【完整解答】甲数×=乙数×,根据比例的基本性质,甲数、乙数、、可以组成比例,
得到甲数∶乙数=∶,化简后甲数∶乙数=6∶5。
故选:A
【考察注意点】本题考查灵活利用比例的基本性质解决问题。
42.A
【思路引导】①判定平年、闰年的方法:普通年份是4的倍数,整百年份是400的倍数,即是闰年;闰年全年366天,平年全年365天;据此判断即可;
②把去年的粮食产量看作单位“1”,今年的粮食产量比去年增加一成,即增加10%,今年的产量是去年产量的(1+10%);据此解答;
③甲∶乙=4∶5,把甲看作4份,乙则有相同的5份,乙比甲多百分之几,以甲作单位“1”,据此用乙比甲多的份数除以甲的份数再乘100%,算出乙比甲多百分之几;
④判断要搞清自然数的分类标准,按质数、合数分,是看一个自然数因数的个数,只有2个因数的是质数,2个以上的是合数;而1是自然数,只有1个因数,所以既不属于质数,也不属于合数,由此判定即可。
【完整解答】①2022÷4=505……2
2022不是4的倍数,所以今年是平年,平年2月只有28天,全年只有365天,所以①说法错误;
②今年的小麦产量比去年增加了一成,把去年小麦产量看作单位“1”,今年小麦产量是去年的1+10%=110%,所以②说法正确;【来源:21cnj*y.co*m】
③甲∶乙=4∶5,把甲看作“4”,乙看作“5”,(5-4)÷4×100%=25%,即乙比甲多25%,所以③说法正确;
④1既不是质数,也不是合数,所以④说法错误。
故选:A
【考察注意点】解答此题时需要灵活运用已学知识,细心分析题中的每一个说法,才能找出正确的选项。
43.D
【思路引导】比例的基本性质:在比例里,两个外项的积等于两个内项的积。
把12A=5B改写成一个外项是A,一个内项是B的比例,则和A相乘的数12就作为比例的另一个外项,和B相乘的数5就作为比例的另一个内项,据此写出比例即可。
【完整解答】因为12A=5B,所以A∶B=5∶12。
故选:D
【考察注意点】解答此题的关键是比例基本性质的逆运用,要注意:相乘的两个数要做外项就都做外项,要做内项就都做内项。
44.A
【思路引导】根据圆柱体积=底面积×高,圆锥体积=×底面积×高,要把圆柱削成一个最大的圆锥,则这个圆锥的体积是圆柱的。据此解答。
【完整解答】120×=40(立方分米)
圆锥的体积是40立方分米。
故选:A
【考察注意点】本题考查了圆柱、圆锥的体积以及它们之间的关系。
45.C
【思路引导】根据折扣、成数、税率、利率知识可知:打几折,就是按照原价的百分之几十出售;农业收成几成就是百分之几十;税率就是应纳税额与各种收入中应纳税部分的百分比,几成解答即可。
【完整解答】A.某商品打七五折出售,就是按原价的75%出售,选项说法正确;
B.农业收成,经常用“成数”表示,三成五就是35%,选项说法正确;
C.优惠三折表示现价是原价的70%,选项说法错误;
D.税率指应纳税额与各种收入中应纳税部分的百分比,选项说法正确;
故选:C
【考察注意点】本题考查了折扣、成数、税率、利率知识,结合题意分析解答即可。
46.B
【思路引导】根据比例尺的意义∶比例尺是图上距离和实际距离的比,代入数据,进行解答即可。
【完整解答】210千米=21000000厘米,一“拃”大约是21厘米,
21∶21000000=1∶1000000
故选:B
【考察注意点】此类题做题的关键是:利用比例尺的意义,代入数据计算即可。
47.B
【思路引导】长方形硬纸板可以围成圆柱的侧面,分两种情况:(1)以长方形的宽为圆柱的底面周长,长方形的长为圆柱的高,这样的笔筒太高,不符合生活实际;(2)以长方形的长为圆柱的底面周长,长方形的宽为圆柱的高,然后根据r=C÷π÷2,求出圆柱的底面半径;据此选择。
【完整解答】情况一:以长方形的12.56cm作为圆柱的底面周长,25.12cm作为圆柱的高时,笔筒太高,不符合生活实际;
情况二:以长方形的25.12cm作为圆柱的底面周长,12.56cm作为圆柱的高时,圆柱的底面半径是:
25.12÷3.14÷2
=8÷2
=4(cm)
故选:B
【考察注意点】掌握圆柱的侧面展开图的特点,结合实际分情况讨论,灵活运用圆的周长公式是解题的关键。
48.B
【思路引导】设它们的高是h,圆柱的底面半径是1,圆锥的底面半径是2,然后根据圆柱的体积公式:V=Sh,圆锥的体积公式:V=Sh,最后用圆柱的体积比上圆锥的体积即可。
【完整解答】π×12×h∶×π×22×h
=πh∶πh
=1∶
=3∶4
故选:B
【考察注意点】本题考查圆柱和圆锥的体积,熟记公式是解题的关键。
49.A
【思路引导】判断两个相关联的量之间成什么比例,就看这两个量是对应的比值一定,还是对应的乘积一定;如果是比值一定,就成正比例;如果是乘积一定,则成反比例。
【完整解答】因为,所以,商一定,所以x与y成正比例关系。
故选:A
【考察注意点】解答本题的关键就看这两个相关联的量是对应的比值一定,还是对应的乘积一定。
50.C
【思路引导】联系生活实际,按一般情况判断各选项物体的半径与高的尺寸,得出结论。
【完整解答】A.牙签筒的半径<3厘米,高<12厘米,不符合题意;
B.铅笔的半径<3厘米,高>12厘米,不符合题意;
C.水杯的半径约是3厘米,高约是12厘米,符合题意;
D.胶棒的半径<3厘米,高<12厘米,不符合题意。
故选:C
【考察注意点】本题考查圆柱的特征及应用。
51.B
【思路引导】由图可知:切面的长是圆柱的高,宽是圆柱的直径。长方形的面积=长×宽,代入数据求出长方形的长(圆柱的高),再将数据代入圆柱的体积公式计算即可。
【完整解答】60÷6=10(厘米)
3.14×(6÷2)2×10
=3.14×9×10
=3.14×90
=282.6(立方厘米)
故选:B
【考察注意点】本题主要考查立体图形的切拼,明确切面的长是圆柱的高,宽是圆柱的直径是解题的关键。
52.B
【思路引导】比例尺等于图上距离比实际距离,据此先统一单位再做比即可。
【完整解答】6厘米=60毫米,
60∶3=20∶1。
故选:B
【考察注意点】本题考查了比例尺,在求比例尺时,一定要注意先统一单位,避免计算错误。
53.D
【思路引导】图上距离与实际距离的比即为比例尺,实际距离和图上距离已知,代入公式即可求出比例尺。
【完整解答】5厘米=50毫米,
50∶0.5=100∶1;
则这幅图的比例尺是100∶1。
故选:D。
【考察注意点】解答此题的关键是,先统一单位,再代入求比例尺的公式即可。
54.C
【思路引导】由题意可知:甲数乙数,再逆运用比例的基本性质,即两内项之积等于两外项之积,即可求出二者的比。21世纪教育网版权所有
【完整解答】甲数乙数,甲数∶乙数。
故选:C
【考察注意点】此题主要依据比例的基本性质解决问题。
55.B
【思路引导】根据比例的基本性质可知,两个内项的积等于两个外项的积。已知两个内项的积是30,计算四个选项里的乘积,找出结果不是30的选项即可。【版权所有:21教育】
【完整解答】A.30×1=30,30=30;所以这两个外项是可能的;
B.15×5=75,7530;所以这两个外项是不可能的;
C.1.5×20=30,30=30;所以这两个外项是可能的;
D.0.75×40=30,30=30;所以这两个外项是可能的。
故选:B
【考察注意点】此题的解题关键是灵活运用比例的基本性质来求解。
56.C
【思路引导】把圆柱形木料截成3个小圆柱,表面积增加了4个底面的面积,其中一个底面的面积=增加的表面积÷4;原来这根木料的体积=底面积×高。
【完整解答】0.6÷4×2
=0.15×2
=0.3(立方米)
故选:C
【考察注意点】抓住圆柱的切割特点和增加的表面积,先求出圆柱的底面积是解决此类问题的关键。
57.C
【思路引导】根据0的意义,比如相同两个数相减的结果是0;一个数与0相加的和是它本身;一个数减0的差是它本身;0除以任何一个不为0的数商是0;0与任何数相乘的积是0。一个非0的数除以0无意义;0既不是正数也不是负数;逐一判断,可得答案。
【完整解答】A.0乘任何数都等于0表述正确;
B.0和正整数都是自然数表述正确;
C.0能做乘数、减数和除数表述错误,不能做除数;
D.0既不是正数也不是负数表述正确。
故选:C
【考察注意点】此题考查了负数的意义、整数的认识、自然数的认识和乘除法的意义等。
58.B
【思路引导】用正负数表示意义相反的两种量:一种记作正,则和它意义相反的就记作负。由此得解。
【完整解答】根据分析可知,
通常规定海平面的海拔高度为0m,珠穆朗玛峰高出海平面8848.86m,其海拔高度记作﹢8848.86m,吐鲁番盆地的最低处低于海平面154.31m,其海拔高度记作﹣154.31m。
故选:B
【考察注意点】此题主要考查正负数的意义,正数与负数表示意义相反的两种量,看清规定哪一个为正,则和它意义相反的就为负。2-1-c-n-j-y
59.D
【思路引导】根据圆锥的体积公式:V=πr2h,设大圆锥的底面半径为r,高为h,则小圆锥的底面半径为r,高为h,把数据代入公式求出大小圆锥的体积,再根据求一个数是另一个数的几倍,用除法解答。
【完整解答】解:设大圆锥的底面半径为r,高为h,则小圆锥的底面半径为r,高为h;
πr2h÷[π×(r)2×h]
=πr2h÷[π×r2×h]
=πr2h÷[π×r2h]
=8
故选:D
【考察注意点】此题主要考查圆锥体积公式的灵活运用,关键是熟记公式。
60.A
【思路引导】20个学生参加6个兴趣小组,20÷6=3(人)……2(人),即平均每组有3人,还余2人,根据抽屉原理可知,至少有一个兴趣小组的学生不少于3+1=4(人),据此解答。
【完整解答】20÷6=3(人)……2(人)
3+1=4(人)
故选:A
【考察注意点】在此类抽屉问题中,至少数=物体数除以抽屉数的商+1(有余数的情况下)。
61.C
【思路引导】根据利息的计算公式是:本金×利率×存期,可计算出利息(注意公式中的时间和利率要对应)。
【完整解答】利息的计算公式是:利息=本金×利率×存期。
故选:C
【考察注意点】此题主要考查的是利息的计算公式。
62.A
【思路引导】圆柱的侧面沿高剪开的展开图是一个长方形(或正方形)。这个长方形(或正方形)的长等于圆柱底面的周长,依据圆的周长公式将数值代入计算并选择。
【完整解答】A.圆是直径是3,圆的周长是3.14×3=9.42,底面周长等于侧面展开图的长,所以图A是圆柱的展开图;
B.圆是直径是3,圆的周长是3.14×3=9.42,底面周长不等于侧面展开图的长,所以图B不是圆柱的展开图;www-2-1-cnjy-com
C.圆是直径是3,圆的周长是3.14×3=9.42,底面周长不等于侧面展开图的长,所以图C不是圆柱的展开图。
故选:A
【考察注意点】此题考查圆柱的侧面展开图,要明确:沿高线剪开,圆柱的侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高。
63.B
【思路引导】数轴上,0在正数的左边,在负数的右边。据此解题。
【完整解答】﹣是负数,所以在直线上,0在﹣的右边。
故选:B
【考察注意点】本题考查了正负数在数轴上的表示,数轴上正数在0的右边,负数在0的左边。
64.C
【思路引导】根据圆锥的体积公式:,现在的底面半径扩大到原来的3倍,高缩小到原来的,即半径=3r,高=h,代入到体积公式中,观察体积的变化情况。
【完整解答】
=
=
÷=4.5
故选:C
【考察注意点】此题的解题关键是灵活运用圆锥的体积公式,找出变化的规律。
65.D
【思路引导】根据圆柱特征,圆柱底面是一个圆,圆的面积公式为:S=r2,圆柱体积公式:V=Sh,由此可得出圆柱体积公式可以表示为:V=r2h,圆柱的底面半径和高都扩大到原来的2倍,根据积的变化规律:两数相乘,其中一个因数乘m或者除以m(0除外),另一个因数乘n或者除以n(0除外),积就乘mn或者除以mn(0除外),据此判断即可。
【完整解答】由分析可得:
因为V=r2h,因数r扩大到原来的2倍,则r2扩大到原来的倍数为:2×2=4,另一个因数h扩大到原来的2倍,则体积扩大的倍数为:
4×2=8
即体积扩大到原来的8倍。
故选:D
【考察注意点】本题考查了圆柱体积公式的应用,以及积的变化规律的应用。
66.C
【思路引导】由于向四个空容器中分别倒入同样多的水,则容器的底面积越小,容器的水位越高,依此计算四个空容器的底面积进行比较即可求解。
【完整解答】5×4=20(cm2)
4×4=16(cm2)
3×4=12(cm2)
(4÷2)2×3.14
=22×3.14
=4×3.14
=12.56(cm2)
20>16>12.56>12
所以容器C的水位最高。
故选:C
【考察注意点】本题考查了长方体的体积和圆柱的容积,关键是灵活运用长方体的体积和圆柱的容积公式。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
