15.1多边形 课后测评(无答案)2022-2023学年京改版八年级数学下册
文档属性
| 名称 | 15.1多边形 课后测评(无答案)2022-2023学年京改版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 194.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 17:56:07 | ||
图片预览

文档简介
京改版八年级数学下册15.1多边形课后测评
一、单选题
1、如果一个多边形内角和是外角和的4倍,那么这个多边形有( )条对角线.
A.20 B.27 C.35 D.44
2、下列说法中正确的是( )
A.两点之间,直线最短
B.由两条射线组成的图形叫做角
C.若过多边形的一个顶点可以画5条对角线,则这个多边形是八边形
D.对于线段与,若,则点是线段的中点
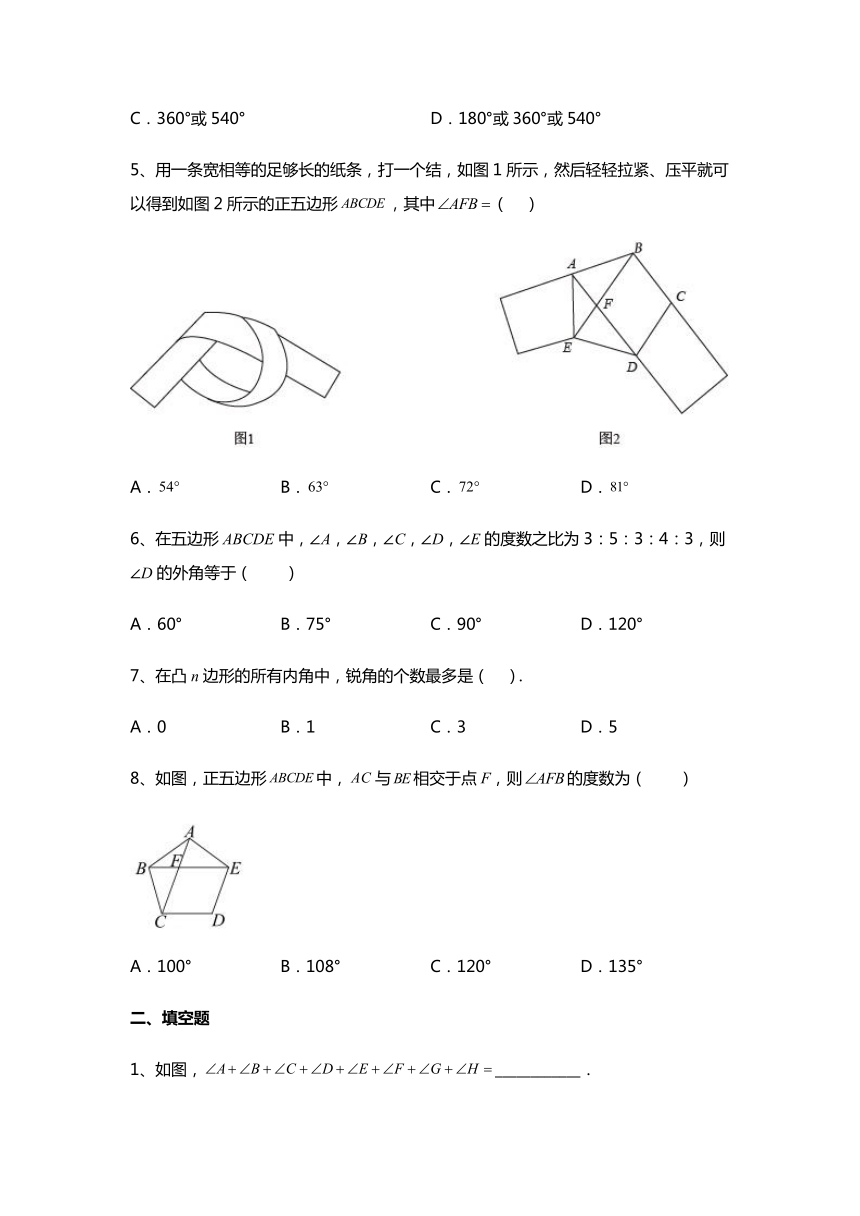
3、如图的电子装置中,红黑两枚跳棋开始放置在边长为2的正六边形的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )
A.4 B. C.2 D.0
4、将一个四边形的纸片剪去一个三角形,则剩下图形的内角和为( ).
A.180° B.180°或360°
C.360°或540° D.180°或360°或540°
5、用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形,其中( )
A. B. C. D.
6、在五边形ABCDE中,∠A,∠B,∠C,∠D,∠E的度数之比为3:5:3:4:3,则∠D的外角等于( )
A.60° B.75° C.90° D.120°
7、在凸n边形的所有内角中,锐角的个数最多是( ).
A.0 B.1 C.3 D.5
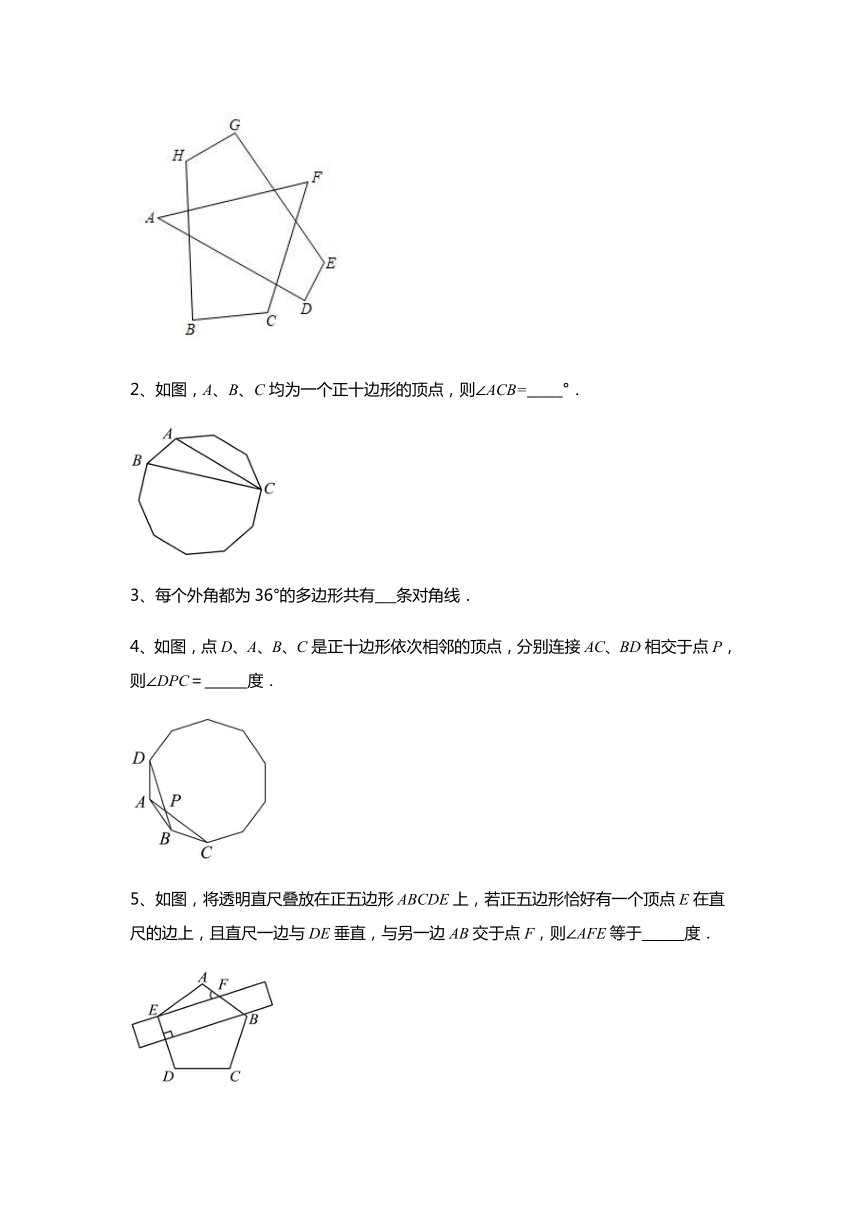
8、如图,正五边形中,与相交于点F,则的度数为( )
A.100° B.108° C.120° D.135°
二、填空题
1、如图,____________.
2、如图,A、B、C均为一个正十边形的顶点,则∠ACB=_____°.
3、每个外角都为36°的多边形共有___条对角线.
4、如图,点D、A、B、C是正十边形依次相邻的顶点,分别连接AC、BD相交于点P,则∠DPC=______度.
5、如图,将透明直尺叠放在正五边形ABCDE上,若正五边形恰好有一个顶点E在直尺的边上,且直尺一边与DE垂直,与另一边AB交于点F,则∠AFE等于______度.
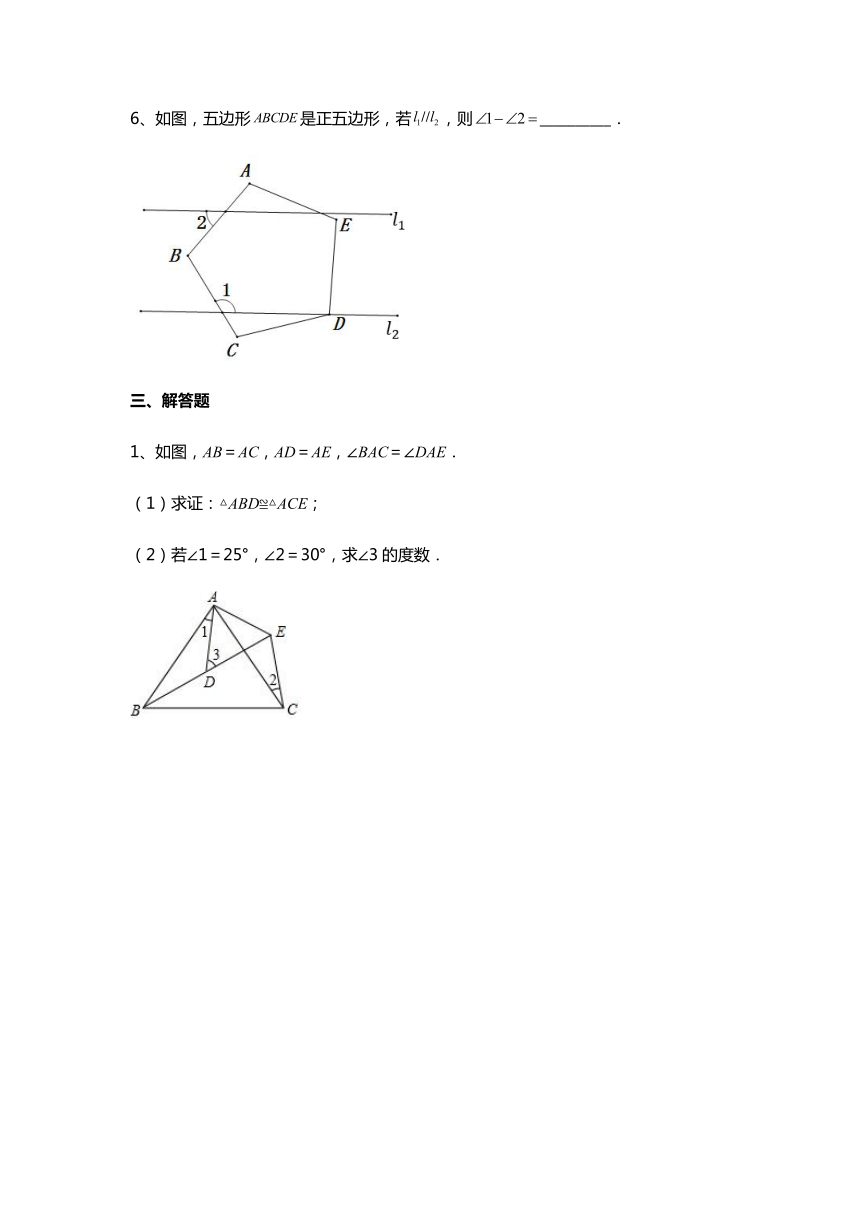
6、如图,五边形是正五边形,若,则__________.
三、解答题
1、如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
2、△ACB和△DCE是共顶点C的两个大小不一样的等边三角形.
(1)问题发现:
如图1,若点A,D,E在同一直线上,连接AE,BE.
①求证:△ACD≌△BCE;
②求∠AEB的度数.
(2)类比探究:如图2,点B、D、E在同一直线上,连接AE,AD,BE,CM为△DCE中DE边上的高,请求∠ADB的度数及线段DB,AD,DM之间的数量关系,并说明理由.
(3)拓展延伸:如图3,若设AD(或其延长线)与BE的所夹锐角为α,则你认为α为多少度,并证明.
3、(1)问题发现:小红在数学课上学习了外角的相关知识后,她很容易地证明了三角形外角的性质,即三角形的一个外角等于与它不相邻的两个内角的和,于是,爱思考的小红在想,四边形的外角是否也具有类似的性质呢?
如图①,∠1,∠2是四边形ABCD的两个外角.
∵四边形ABCD的内角和是360°,
∴∠A+∠D+(∠3+∠4)=360°,
又∵∠1+∠3+∠2+∠4=360°,
由此可得∠1,∠2与∠A,∠D的数量关系是_________________;
(2)总结归纳:如果我们把∠1,∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)知识应用:如图②,已知四边形ABCD,AE,DE分别是其外角∠NAD和∠MDA的平分线,若∠B+∠C=230°,求∠E的度数;
(4)拓展提升:如图③,四边形ABCD中,∠A=∠C=90°,∠CDN和∠CBM是它的两个外角,且∠CDP=∠CDN,∠CBP=∠CBM,求∠P的度数.
4、夏夏和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中,请仔细观察下面的图形和表格,并回答下列问题:
多边形的顶点数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 …… ①
多边形对角线的总条数 2 5 9 14 20 …… ②
(1)观察探究:请自己观察上面的图形和表格,并用含n的代数式将上面的表格填写完整,其中①________;②________.
(2)拓展应用:
有一个76人的代表团,由于任务需要每两人之间通1次电话(且只通1次电话),他们一共通了多少次电话
5、附加题:
探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的△ABC中AB、BC是两腰,所以∠BAC=∠BCA.利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O它们所夹的锐角为a.如图:
正五边形α=_____;正六边形α=______;正八边α=_____;当正多边形的边数是n时,α=______.
6、如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E是AD上一点,F是AB延长线上一点,且DE=BF.
(1)求证:CE=CF;
(2)若G在AB上且∠ECG=60°,试猜想DE,EG,BG之间的数量关系,并证明.
一、单选题
1、如果一个多边形内角和是外角和的4倍,那么这个多边形有( )条对角线.
A.20 B.27 C.35 D.44
2、下列说法中正确的是( )
A.两点之间,直线最短
B.由两条射线组成的图形叫做角
C.若过多边形的一个顶点可以画5条对角线,则这个多边形是八边形
D.对于线段与,若,则点是线段的中点
3、如图的电子装置中,红黑两枚跳棋开始放置在边长为2的正六边形的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )
A.4 B. C.2 D.0
4、将一个四边形的纸片剪去一个三角形,则剩下图形的内角和为( ).
A.180° B.180°或360°
C.360°或540° D.180°或360°或540°
5、用一条宽相等的足够长的纸条,打一个结,如图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形,其中( )
A. B. C. D.
6、在五边形ABCDE中,∠A,∠B,∠C,∠D,∠E的度数之比为3:5:3:4:3,则∠D的外角等于( )
A.60° B.75° C.90° D.120°
7、在凸n边形的所有内角中,锐角的个数最多是( ).
A.0 B.1 C.3 D.5
8、如图,正五边形中,与相交于点F,则的度数为( )
A.100° B.108° C.120° D.135°
二、填空题
1、如图,____________.
2、如图,A、B、C均为一个正十边形的顶点,则∠ACB=_____°.
3、每个外角都为36°的多边形共有___条对角线.
4、如图,点D、A、B、C是正十边形依次相邻的顶点,分别连接AC、BD相交于点P,则∠DPC=______度.
5、如图,将透明直尺叠放在正五边形ABCDE上,若正五边形恰好有一个顶点E在直尺的边上,且直尺一边与DE垂直,与另一边AB交于点F,则∠AFE等于______度.
6、如图,五边形是正五边形,若,则__________.
三、解答题
1、如图,AB=AC,AD=AE,∠BAC=∠DAE.
(1)求证:△ABD≌△ACE;
(2)若∠1=25°,∠2=30°,求∠3的度数.
2、△ACB和△DCE是共顶点C的两个大小不一样的等边三角形.
(1)问题发现:
如图1,若点A,D,E在同一直线上,连接AE,BE.
①求证:△ACD≌△BCE;
②求∠AEB的度数.
(2)类比探究:如图2,点B、D、E在同一直线上,连接AE,AD,BE,CM为△DCE中DE边上的高,请求∠ADB的度数及线段DB,AD,DM之间的数量关系,并说明理由.
(3)拓展延伸:如图3,若设AD(或其延长线)与BE的所夹锐角为α,则你认为α为多少度,并证明.
3、(1)问题发现:小红在数学课上学习了外角的相关知识后,她很容易地证明了三角形外角的性质,即三角形的一个外角等于与它不相邻的两个内角的和,于是,爱思考的小红在想,四边形的外角是否也具有类似的性质呢?
如图①,∠1,∠2是四边形ABCD的两个外角.
∵四边形ABCD的内角和是360°,
∴∠A+∠D+(∠3+∠4)=360°,
又∵∠1+∠3+∠2+∠4=360°,
由此可得∠1,∠2与∠A,∠D的数量关系是_________________;
(2)总结归纳:如果我们把∠1,∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)知识应用:如图②,已知四边形ABCD,AE,DE分别是其外角∠NAD和∠MDA的平分线,若∠B+∠C=230°,求∠E的度数;
(4)拓展提升:如图③,四边形ABCD中,∠A=∠C=90°,∠CDN和∠CBM是它的两个外角,且∠CDP=∠CDN,∠CBP=∠CBM,求∠P的度数.
4、夏夏和数学小组的同学们研究多边形对角线的相关问题,邀请你也加入其中,请仔细观察下面的图形和表格,并回答下列问题:
多边形的顶点数 4 5 6 7 8 ……
从一个顶点出发的对角线的条数 1 2 3 4 5 …… ①
多边形对角线的总条数 2 5 9 14 20 …… ②
(1)观察探究:请自己观察上面的图形和表格,并用含n的代数式将上面的表格填写完整,其中①________;②________.
(2)拓展应用:
有一个76人的代表团,由于任务需要每两人之间通1次电话(且只通1次电话),他们一共通了多少次电话
5、附加题:
探究题:我们知道等腰三角形的两个底角相等,如下面每个图中的△ABC中AB、BC是两腰,所以∠BAC=∠BCA.利用这条性质,解决下面的问题:
已知下面的正多边形中,相邻四个顶点连接的对角线交于点O它们所夹的锐角为a.如图:
正五边形α=_____;正六边形α=______;正八边α=_____;当正多边形的边数是n时,α=______.
6、如图,在四边形ABCD中,AD=AB,DC=BC,∠DAB=60°,∠DCB=120°,E是AD上一点,F是AB延长线上一点,且DE=BF.
(1)求证:CE=CF;
(2)若G在AB上且∠ECG=60°,试猜想DE,EG,BG之间的数量关系,并证明.
同课章节目录
