人教版八年级下册17.1勾股定理 同步练习(含解析)
文档属性
| 名称 | 人教版八年级下册17.1勾股定理 同步练习(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 549.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 18:18:20 | ||
图片预览




文档简介
17.1 勾股定理 同步练习
一、单选题
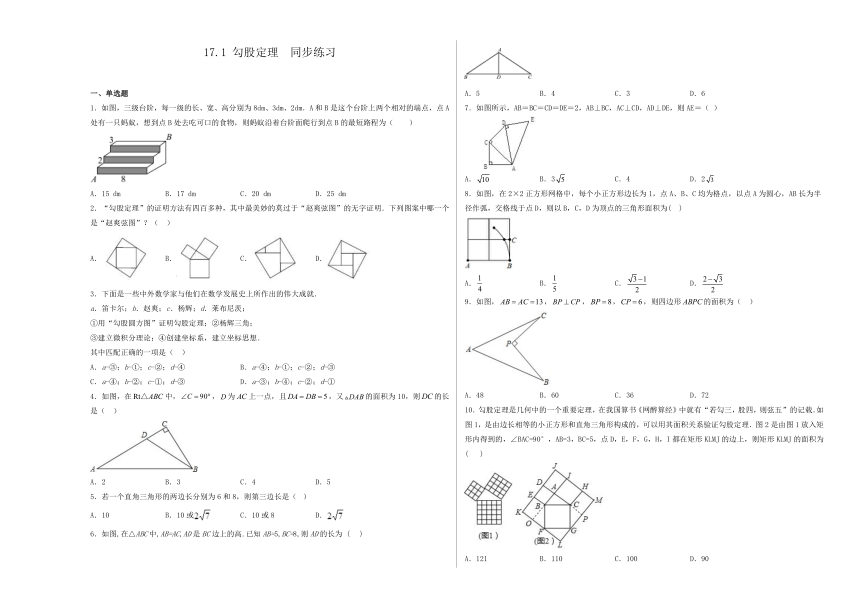
1.如图,三级台阶,每一级的长、宽、高分别为8dm、3dm、2dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
A.15 dm B.17 dm C.20 dm D.25 dm
2.“勾股定理”的证明方法有四百多种,其中最美妙的莫过于“赵爽弦图”的无字证明.下列图案中哪一个是“赵爽弦图”?( )
A. B. C. D.
3.下面是一些中外数学家与他们在数学发展史上所作出的伟大成就.
a.笛卡尔;b.赵爽;c.杨辉;d.莱布尼茨;
①用“勾股圆方图”证明勾股定理;②杨辉三角;
③建立微积分理论;④创建坐标系,建立坐标思想.
其中匹配正确的一项是( )
A.a-③;b-①;c-②;d-④ B.a-④;b-①;c-②;d-③
C.a-④;b-②;c-①;d-③ D.a-③;b-④;c-②;d-①
4.如图,在中,,为上一点,且,又的面积为10,则的长是( )
A.2 B.3 C.4 D.5
5.若一个直角三角形的两边长分别为6和8,则第三边长是( )
A.10 B.10或 C.10或8 D.
6.如图,在△ABC中,AB=AC,AD是BC边上的高.已知AB=5,BC=8,则AD的长为 ( )
A.5 B.4 C.3 D.6
7.如图所示,AB=BC=CD=DE=2,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
A. B.3 C.4 D.2
8.如图,在2×2正方形网格中,每个小正方形边长为1,点A、B、C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则以B,C,D为顶点的三角形面积为( )
A. B. C. D.
9.如图,,,,,则四边形的面积为( )
A.48 B.60 C.36 D.72
10.勾股定理是几何中的一个重要定理,在我国算书《网醉算经》中就有“若勾三,股四,则弦五”的记载.如图1,是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,BC=5,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
A.121 B.110 C.100 D.90
二、填空题
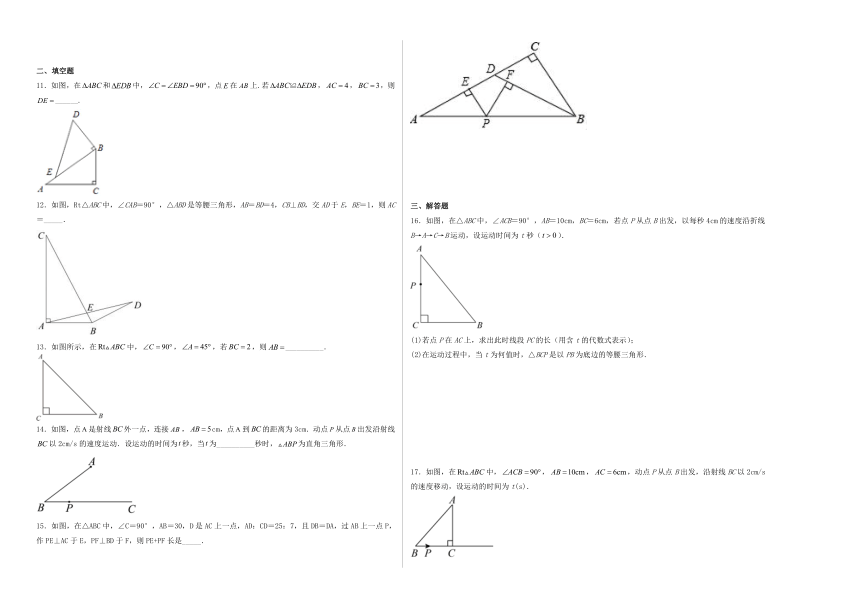
11.如图,在和中,,点在上.若,,,则______.
12.如图,Rt△ABC中,∠CAB=90°,△ABD是等腰三角形,AB=BD=4,CB⊥BD,交AD于E,BE=1,则AC=_____.
13.如图所示,在中,,,若,则__________.
14.如图,点是射线外一点,连接,cm,点到的距离为3cm.动点从点出发沿射线以2cm/s的速度运动.设运动的时间为秒,当为__________秒时,为直角三角形.
15.如图,在△ABC中,∠C=90°,AB=30,D是AC上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是_____.
三、解答题
16.如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点B出发,以每秒4cm的速度沿折线B→A→C→B运动,设运动时间为t秒().
(1)若点P在AC上,求出此时线段PC的长(用含t的代数式表示);
(2)在运动过程中,当t为何值时,△BCP是以PB为底边的等腰三角形.
17.如图,在中,,,,动点P从点B出发,沿射线BC以2cm/s的速度移动,设运动的时间为t(s).
(1)求BC边的长.
(2)当为直角三角形时,求t的值.
18.如图所示,在一棵树的10米高的处有两只猴子,一只猴子爬下树走到离树20米的处.另一只猴子爬到树顶处后顺绳子滑到处,如果两只猴子所经过的距离相等,求这棵树的高.
参考答案:
1.B
【详解】最短路径
故答案为:B.
2.D
【详解】由“赵爽弦图”的图形特征可知选D
故选:D.
3.B
【详解】解:根据笛卡尔创建坐标系,建立坐标思想;赵爽用“勾股圆方图”证明勾股定理;杨辉发现了杨辉三角;莱布尼茨建立微积分理论;
即a-④;b-①;c-②;d-③,
故选:B.
4.B
【详解】解:∵
∴DA·BC=20
∵DA=5
∴BC=4
在Rt△BCD中,BC=4,DB=5
∴CD=.
故选B.
5.B
【详解】试题分析:①当8cm是斜边时,第三边长=cm;②当6cm和8cm是直角边时,第三边长=cm;故第三边的长为:cm或10cm.故选B.
考点:1.勾股定理;2.分类讨论.
6.C
【详解】解:∵AB=AC,AD是BC边上的高,AB=5,BC=8.
∴BD=BC=4,
由勾股定理得,AD= =3(cm),
故选C.
7.D
【详解】在Rt△ABC中,由勾股定理得.
在Rt△ADC中,由勾股定理得.
在Rt△ADE中,由勾股定理得.
8.D
【详解】解:连接AD,
由勾股定理得,DE= ,
∴CD=EC-ED=2- ,
∴△BCD的面积= ,
故选D.
9.C
【详解】解:如图,连接,过点作于点,
∵,,,
∴,
∵,,
∴,
在中,
∴四边形的面积为
,
故选:C.
10.B
【详解】解:如图,延长交于点,延长交于点,则四边形是矩形.
,
,
又直角中,,
,
在和中,
,
,
,
同理:,
,
,
所以,矩形是正方形,
边长,
所以,,,
因此,矩形的面积为,
故选B.
11.5
【详解】解:在Rt△ACB中,∠C=90°,AC=4,BC=3,
由勾股定理得:AB=5,
∵△ABC≌△EDB,
∴DE=AB=5.
12.
【详解】∵AB=BD=4,
∴∠BAE=∠BDE,
又∵CB⊥BD,
∴∠DBE=∠CAB=90°,
∴∠DEB=90°-∠BDE,
∠CAE=90°-∠BAE,
∴∠CAE=∠DEB,
又∵∠CAE=∠DEB,
∴∠CAE=∠CEA,
∴AC=EC,
又∵BE=1,
∴BC=AC+1,
在Rt△ABC中,有勾股定理可知:AC +AB =BC ,
∴AC +4 =(AC+1) ,
∴AC=,
故答案为:.
13.
【详解】在中,,
是等腰直角三角形
故答案为:.
14.2或
【详解】解:①如图1,当∠APB=90°时,
由题意得:AP=3cm,
∴(cm),
∴t=(秒);
②如图2,当∠BAP=90°时,过点A作AD⊥BC于D,
由①可知,AD=3,BD=4,
在Rt△ADP中,AD2+DP2=AP2,
∴32+DP2=AP2,
在Rt△BAP中,AB2+AP2=BP2,
∴,
∴,
∴BP=4+=,
∴秒,
综上,当为2秒或秒时,为直角三角形.
15.18
【详解】解:如图连接DP,设AD=BD=25k,CD=7k,
在Rt△DCB中,BC= =24k,
在Rt△ACB中,∵AC2+BC2=AB2,
∴(32k)2+(24k)2=302,
∴k=,
∴BC=18,
∵S△ABD= AD BC= AD PE+ BD PF,AD=BD
∴PE+PF=BC=18,
故答案为18
16【详解】(1)解:∵△ABC中,∠ACB=90°,AB=10cm,BC=6cm,
∴由勾股定理得AC==8cm,
AB+AC=10+8=18cm
∴PC=18-4t.
∴线段PC的长为(18-4t)cm.
(2)解:当点P在AB边上且PC=BC时,
过点C做CD⊥AB于点D,则PB=2BD
∵,
∴
∴,
∴
即,
∴.
当点P在AC边上时,则PC=BC
即18-4t=6,
∴t=3
综合上述,当或t=3时,△BCP是以PB为底的等腰三角形.
17.
(1)在中,
由勾股定理得,
∴.
(2)
由题意知.
①当时,如图1,点P与点C重合,,
∴.
②当时,如图2,,.
在中,,
在中,,
因此,
解得.
综上所述,当为直角三角形时,t的值为4或.
图1 图2
18解:设树高为米,由题意得,米,米,米,米,
在中, .
∵两只猴子所经过的距离相等,,
即,解得:,即树高米.
答:这棵树的高为米.
一、单选题
1.如图,三级台阶,每一级的长、宽、高分别为8dm、3dm、2dm.A和B是这个台阶上两个相对的端点,点A处有一只蚂蚁,想到点B处去吃可口的食物,则蚂蚁沿着台阶面爬行到点B的最短路程为( )
A.15 dm B.17 dm C.20 dm D.25 dm
2.“勾股定理”的证明方法有四百多种,其中最美妙的莫过于“赵爽弦图”的无字证明.下列图案中哪一个是“赵爽弦图”?( )
A. B. C. D.
3.下面是一些中外数学家与他们在数学发展史上所作出的伟大成就.
a.笛卡尔;b.赵爽;c.杨辉;d.莱布尼茨;
①用“勾股圆方图”证明勾股定理;②杨辉三角;
③建立微积分理论;④创建坐标系,建立坐标思想.
其中匹配正确的一项是( )
A.a-③;b-①;c-②;d-④ B.a-④;b-①;c-②;d-③
C.a-④;b-②;c-①;d-③ D.a-③;b-④;c-②;d-①
4.如图,在中,,为上一点,且,又的面积为10,则的长是( )
A.2 B.3 C.4 D.5
5.若一个直角三角形的两边长分别为6和8,则第三边长是( )
A.10 B.10或 C.10或8 D.
6.如图,在△ABC中,AB=AC,AD是BC边上的高.已知AB=5,BC=8,则AD的长为 ( )
A.5 B.4 C.3 D.6
7.如图所示,AB=BC=CD=DE=2,AB⊥BC,AC⊥CD,AD⊥DE,则AE=( )
A. B.3 C.4 D.2
8.如图,在2×2正方形网格中,每个小正方形边长为1,点A、B、C均为格点,以点A为圆心,AB长为半径作弧,交格线于点D,则以B,C,D为顶点的三角形面积为( )
A. B. C. D.
9.如图,,,,,则四边形的面积为( )
A.48 B.60 C.36 D.72
10.勾股定理是几何中的一个重要定理,在我国算书《网醉算经》中就有“若勾三,股四,则弦五”的记载.如图1,是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入矩形内得到的,∠BAC=90°,AB=3,BC=5,点D,E,F,G,H,I都在矩形KLMJ的边上,则矩形KLMJ的面积为( )
A.121 B.110 C.100 D.90
二、填空题
11.如图,在和中,,点在上.若,,,则______.
12.如图,Rt△ABC中,∠CAB=90°,△ABD是等腰三角形,AB=BD=4,CB⊥BD,交AD于E,BE=1,则AC=_____.
13.如图所示,在中,,,若,则__________.
14.如图,点是射线外一点,连接,cm,点到的距离为3cm.动点从点出发沿射线以2cm/s的速度运动.设运动的时间为秒,当为__________秒时,为直角三角形.
15.如图,在△ABC中,∠C=90°,AB=30,D是AC上一点,AD:CD=25:7,且DB=DA,过AB上一点P,作PE⊥AC于E,PF⊥BD于F,则PE+PF长是_____.
三、解答题
16.如图,在△ABC中,∠ACB=90°,AB=10cm,BC=6cm,若点P从点B出发,以每秒4cm的速度沿折线B→A→C→B运动,设运动时间为t秒().
(1)若点P在AC上,求出此时线段PC的长(用含t的代数式表示);
(2)在运动过程中,当t为何值时,△BCP是以PB为底边的等腰三角形.
17.如图,在中,,,,动点P从点B出发,沿射线BC以2cm/s的速度移动,设运动的时间为t(s).
(1)求BC边的长.
(2)当为直角三角形时,求t的值.
18.如图所示,在一棵树的10米高的处有两只猴子,一只猴子爬下树走到离树20米的处.另一只猴子爬到树顶处后顺绳子滑到处,如果两只猴子所经过的距离相等,求这棵树的高.
参考答案:
1.B
【详解】最短路径
故答案为:B.
2.D
【详解】由“赵爽弦图”的图形特征可知选D
故选:D.
3.B
【详解】解:根据笛卡尔创建坐标系,建立坐标思想;赵爽用“勾股圆方图”证明勾股定理;杨辉发现了杨辉三角;莱布尼茨建立微积分理论;
即a-④;b-①;c-②;d-③,
故选:B.
4.B
【详解】解:∵
∴DA·BC=20
∵DA=5
∴BC=4
在Rt△BCD中,BC=4,DB=5
∴CD=.
故选B.
5.B
【详解】试题分析:①当8cm是斜边时,第三边长=cm;②当6cm和8cm是直角边时,第三边长=cm;故第三边的长为:cm或10cm.故选B.
考点:1.勾股定理;2.分类讨论.
6.C
【详解】解:∵AB=AC,AD是BC边上的高,AB=5,BC=8.
∴BD=BC=4,
由勾股定理得,AD= =3(cm),
故选C.
7.D
【详解】在Rt△ABC中,由勾股定理得.
在Rt△ADC中,由勾股定理得.
在Rt△ADE中,由勾股定理得.
8.D
【详解】解:连接AD,
由勾股定理得,DE= ,
∴CD=EC-ED=2- ,
∴△BCD的面积= ,
故选D.
9.C
【详解】解:如图,连接,过点作于点,
∵,,,
∴,
∵,,
∴,
在中,
∴四边形的面积为
,
故选:C.
10.B
【详解】解:如图,延长交于点,延长交于点,则四边形是矩形.
,
,
又直角中,,
,
在和中,
,
,
,
同理:,
,
,
所以,矩形是正方形,
边长,
所以,,,
因此,矩形的面积为,
故选B.
11.5
【详解】解:在Rt△ACB中,∠C=90°,AC=4,BC=3,
由勾股定理得:AB=5,
∵△ABC≌△EDB,
∴DE=AB=5.
12.
【详解】∵AB=BD=4,
∴∠BAE=∠BDE,
又∵CB⊥BD,
∴∠DBE=∠CAB=90°,
∴∠DEB=90°-∠BDE,
∠CAE=90°-∠BAE,
∴∠CAE=∠DEB,
又∵∠CAE=∠DEB,
∴∠CAE=∠CEA,
∴AC=EC,
又∵BE=1,
∴BC=AC+1,
在Rt△ABC中,有勾股定理可知:AC +AB =BC ,
∴AC +4 =(AC+1) ,
∴AC=,
故答案为:.
13.
【详解】在中,,
是等腰直角三角形
故答案为:.
14.2或
【详解】解:①如图1,当∠APB=90°时,
由题意得:AP=3cm,
∴(cm),
∴t=(秒);
②如图2,当∠BAP=90°时,过点A作AD⊥BC于D,
由①可知,AD=3,BD=4,
在Rt△ADP中,AD2+DP2=AP2,
∴32+DP2=AP2,
在Rt△BAP中,AB2+AP2=BP2,
∴,
∴,
∴BP=4+=,
∴秒,
综上,当为2秒或秒时,为直角三角形.
15.18
【详解】解:如图连接DP,设AD=BD=25k,CD=7k,
在Rt△DCB中,BC= =24k,
在Rt△ACB中,∵AC2+BC2=AB2,
∴(32k)2+(24k)2=302,
∴k=,
∴BC=18,
∵S△ABD= AD BC= AD PE+ BD PF,AD=BD
∴PE+PF=BC=18,
故答案为18
16【详解】(1)解:∵△ABC中,∠ACB=90°,AB=10cm,BC=6cm,
∴由勾股定理得AC==8cm,
AB+AC=10+8=18cm
∴PC=18-4t.
∴线段PC的长为(18-4t)cm.
(2)解:当点P在AB边上且PC=BC时,
过点C做CD⊥AB于点D,则PB=2BD
∵,
∴
∴,
∴
即,
∴.
当点P在AC边上时,则PC=BC
即18-4t=6,
∴t=3
综合上述,当或t=3时,△BCP是以PB为底的等腰三角形.
17.
(1)在中,
由勾股定理得,
∴.
(2)
由题意知.
①当时,如图1,点P与点C重合,,
∴.
②当时,如图2,,.
在中,,
在中,,
因此,
解得.
综上所述,当为直角三角形时,t的值为4或.
图1 图2
18解:设树高为米,由题意得,米,米,米,米,
在中, .
∵两只猴子所经过的距离相等,,
即,解得:,即树高米.
答:这棵树的高为米.
