2.2.1 分子结构的测定 多样的分子空间结构 课件(共18张PPT) 2022-2023学年高二化学人教版(2019)选择性必修2
文档属性
| 名称 | 2.2.1 分子结构的测定 多样的分子空间结构 课件(共18张PPT) 2022-2023学年高二化学人教版(2019)选择性必修2 |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 化学 | ||
| 更新时间 | 2023-03-13 09:32:07 | ||
图片预览




文档简介
(共18张PPT)
第二章 分子结构与性质
第二节 分子的空间结构
1、分子结构的测定、多样的分子空间结构
回顾旧知
共价键
σ键
π键
键参数
键能
键长
键角
衡量化学键稳定性
描述分子的立体结构的重要因素
成键方式 “头碰头”,
呈轴对称。
成键方式 “肩并肩”,
呈镜像对称。
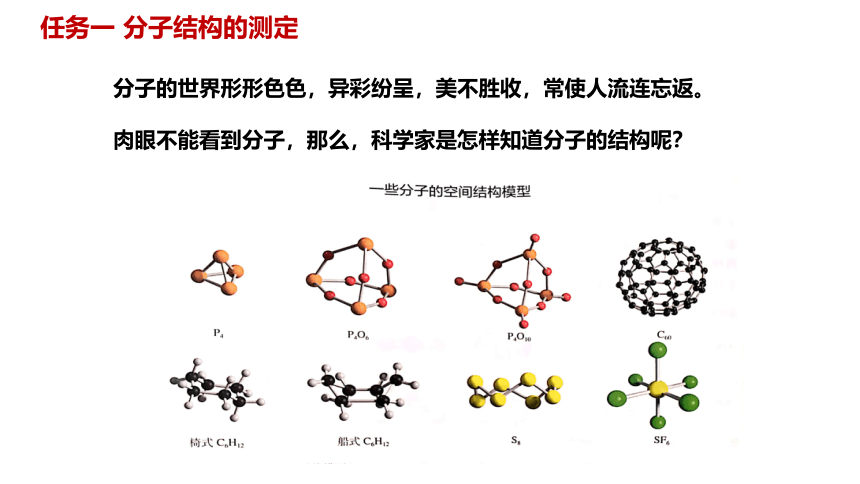
任务一 分子结构的测定
分子的世界形形色色,异彩纷呈,美不胜收,常使人流连忘返。
肉眼不能看到分子,那么,科学家是怎样知道分子的结构呢?
任务一 分子结构的测定
红外光谱仪
X射线衍射仪
质谱仪
早年的科学家主要靠对物质的化学性质进行系统总结得出规律后推测分子的结构。
如今,科学家应用了许多测定分子结构的现代仪器和方法,如红外光谱、晶体X射线衍射等。
任务一 分子结构的测定
1、红外光谱仪
分子中的原子不是固定不动的,而是不断地振动着的。当一束红外线透过分子时,分子会吸收跟它的某些化学键振动频率相同的红外线,再记录到图谱上呈现吸收峰。通过和已有谱库比对,或通过量子化学计算,可以得知各吸收峰是由哪种化学键、哪种振动方式引起的,综合这此信息,可分析出分中含有何种化学键或官能团的信息。
任务一 分子结构的测定
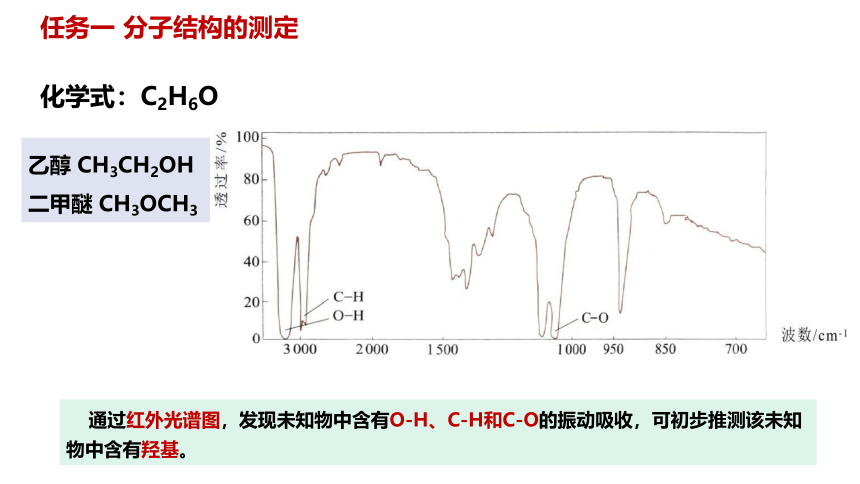
通过红外光谱图,发现未知物中含有O-H、C-H和C-O的振动吸收,可初步推测该未知物中含有羟基。
化学式:C2H6O
乙醇 CH3CH2OH
二甲醚 CH3OCH3
任务一 分子结构的测定
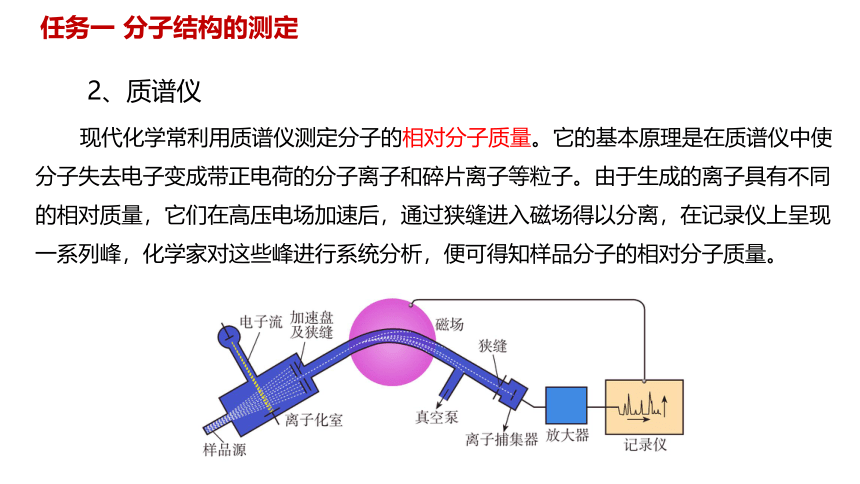
2、质谱仪
现代化学常利用质谱仪测定分子的相对分子质量。它的基本原理是在质谱仪中使分子失去电子变成带正电荷的分子离子和碎片离子等粒子。由于生成的离子具有不同的相对质量,它们在高压电场加速后,通过狭缝进入磁场得以分离,在记录仪上呈现一系列峰,化学家对这些峰进行系统分析,便可得知样品分子的相对分子质量。
任务一 分子结构的测定
纵坐标表示相对丰度(与粒子的浓度成正比),横坐标表示粒子的相对质量与其电荷数之比(m/z),简称荷质比,化学家通过分析得知,被测物的相对分子质量是92,该物质是甲苯。
最大的质荷比就是相对分子质量
任务二 多样的分子空间结构
【思考与讨论】
1、利用几何知识分析一下,空间分布的两个点是否一定在同一直线?
迁移:两个原子构成的分子,将这2个原子看成两个点,则它们在空间上可能构成几种形状?分别是什么?
O2
HCl
【思考与讨论】
2、利用几何知识分析一下,空间分布的三个点是否一定在同一直线上?
任务二 多样的分子空间结构
迁移:三个原子构成的分子,将这3个原子看成三个点,则它们在空间上可能构成几种形状?分别是什么?
CO2
H2O
任务二 多样的分子空间结构
O2
HCl
1、双原子分子(直线形)
任务二 多样的分子空间结构
化学式 电子式 结构式 键角 分子的空间结构模型 空间结构
空间充填模型 球棍模型
CO2
H2O
O
:
:
:
C
O
:
:
:
:
:
H
:
O
H
:
:
:
O=C=O
180°
直线形
V形
105°
2、三原子(AB2型)分子的空间结构——直线形和V形
任务二 多样的分子空间结构
化学式 电子式 结构式 键角 分子的空间结构模型 空间结构
空间充填模型 球棍模型
CH2O
NH3
H
:
C
O
:
:
:
:
:
H
H
:
N
H
:
:
:
H
120°
107°
平面三角形
三角锥形
3、四原子(AB3型)分子的空间结构——平面三角形和三角锥形
任务二 多样的分子空间结构
C2H2 180°
P4 60°正四面体形
BF3
平面正三角形 120°
四原子分子其他立体构型(直线形、正四面体形)
任务二 多样的分子空间结构
化学式 电子式 结构式 键角 分子的空间结构模型 空间结构
空间充填模型 球棍模型
CH4
109°28'
正四面体形
H
:
C
H
:
:
:
H
H
4、五原子(AB4型)分子的空间结构——正四面体形
任务二 多样的分子空间结构
5、其他多原子分子
评价任务
1.可以准确判断有机物分子中含有哪些官能团的分析方法是( )
A.核磁共振氢谱 B.质谱
C.红外光谱 D.紫外光谱
C
2.某有机化合物由碳、氢、氧三种元素组成,其红外光谱图只有C—H、O—H、C—O的振动吸收,该有机物的相对分子质量是60,则该有机物的结构简式是( )
A.CH3CH2OCH3 B.CH3CH(OH)CH3
C.CH3CH2OH D.CH3COOH
B
3.下列说法正确的是( )
A.CS2分子的立体构型是V形
B.NF3分子的立体构型是四面体形
C.键长、键角不同是导致分子构型不同的主要原因
D.正四面体形分子一定是五原子分子
C
4.下列叙述正确的是 ( )
A. NH3分子中N原子处在3个H原子所组成的三角形的中心
B. CCl4分子中C原子处在4个Cl原子所组成的正方形的中心
C. H2O分子中O原子不处在2个H原子所连成的直线的中央
D. CO2分子中C原子不处在2个O原子所连成的直线的中央
C
第二章 分子结构与性质
第二节 分子的空间结构
1、分子结构的测定、多样的分子空间结构
回顾旧知
共价键
σ键
π键
键参数
键能
键长
键角
衡量化学键稳定性
描述分子的立体结构的重要因素
成键方式 “头碰头”,
呈轴对称。
成键方式 “肩并肩”,
呈镜像对称。
任务一 分子结构的测定
分子的世界形形色色,异彩纷呈,美不胜收,常使人流连忘返。
肉眼不能看到分子,那么,科学家是怎样知道分子的结构呢?
任务一 分子结构的测定
红外光谱仪
X射线衍射仪
质谱仪
早年的科学家主要靠对物质的化学性质进行系统总结得出规律后推测分子的结构。
如今,科学家应用了许多测定分子结构的现代仪器和方法,如红外光谱、晶体X射线衍射等。
任务一 分子结构的测定
1、红外光谱仪
分子中的原子不是固定不动的,而是不断地振动着的。当一束红外线透过分子时,分子会吸收跟它的某些化学键振动频率相同的红外线,再记录到图谱上呈现吸收峰。通过和已有谱库比对,或通过量子化学计算,可以得知各吸收峰是由哪种化学键、哪种振动方式引起的,综合这此信息,可分析出分中含有何种化学键或官能团的信息。
任务一 分子结构的测定
通过红外光谱图,发现未知物中含有O-H、C-H和C-O的振动吸收,可初步推测该未知物中含有羟基。
化学式:C2H6O
乙醇 CH3CH2OH
二甲醚 CH3OCH3
任务一 分子结构的测定
2、质谱仪
现代化学常利用质谱仪测定分子的相对分子质量。它的基本原理是在质谱仪中使分子失去电子变成带正电荷的分子离子和碎片离子等粒子。由于生成的离子具有不同的相对质量,它们在高压电场加速后,通过狭缝进入磁场得以分离,在记录仪上呈现一系列峰,化学家对这些峰进行系统分析,便可得知样品分子的相对分子质量。
任务一 分子结构的测定
纵坐标表示相对丰度(与粒子的浓度成正比),横坐标表示粒子的相对质量与其电荷数之比(m/z),简称荷质比,化学家通过分析得知,被测物的相对分子质量是92,该物质是甲苯。
最大的质荷比就是相对分子质量
任务二 多样的分子空间结构
【思考与讨论】
1、利用几何知识分析一下,空间分布的两个点是否一定在同一直线?
迁移:两个原子构成的分子,将这2个原子看成两个点,则它们在空间上可能构成几种形状?分别是什么?
O2
HCl
【思考与讨论】
2、利用几何知识分析一下,空间分布的三个点是否一定在同一直线上?
任务二 多样的分子空间结构
迁移:三个原子构成的分子,将这3个原子看成三个点,则它们在空间上可能构成几种形状?分别是什么?
CO2
H2O
任务二 多样的分子空间结构
O2
HCl
1、双原子分子(直线形)
任务二 多样的分子空间结构
化学式 电子式 结构式 键角 分子的空间结构模型 空间结构
空间充填模型 球棍模型
CO2
H2O
O
:
:
:
C
O
:
:
:
:
:
H
:
O
H
:
:
:
O=C=O
180°
直线形
V形
105°
2、三原子(AB2型)分子的空间结构——直线形和V形
任务二 多样的分子空间结构
化学式 电子式 结构式 键角 分子的空间结构模型 空间结构
空间充填模型 球棍模型
CH2O
NH3
H
:
C
O
:
:
:
:
:
H
H
:
N
H
:
:
:
H
120°
107°
平面三角形
三角锥形
3、四原子(AB3型)分子的空间结构——平面三角形和三角锥形
任务二 多样的分子空间结构
C2H2 180°
P4 60°正四面体形
BF3
平面正三角形 120°
四原子分子其他立体构型(直线形、正四面体形)
任务二 多样的分子空间结构
化学式 电子式 结构式 键角 分子的空间结构模型 空间结构
空间充填模型 球棍模型
CH4
109°28'
正四面体形
H
:
C
H
:
:
:
H
H
4、五原子(AB4型)分子的空间结构——正四面体形
任务二 多样的分子空间结构
5、其他多原子分子
评价任务
1.可以准确判断有机物分子中含有哪些官能团的分析方法是( )
A.核磁共振氢谱 B.质谱
C.红外光谱 D.紫外光谱
C
2.某有机化合物由碳、氢、氧三种元素组成,其红外光谱图只有C—H、O—H、C—O的振动吸收,该有机物的相对分子质量是60,则该有机物的结构简式是( )
A.CH3CH2OCH3 B.CH3CH(OH)CH3
C.CH3CH2OH D.CH3COOH
B
3.下列说法正确的是( )
A.CS2分子的立体构型是V形
B.NF3分子的立体构型是四面体形
C.键长、键角不同是导致分子构型不同的主要原因
D.正四面体形分子一定是五原子分子
C
4.下列叙述正确的是 ( )
A. NH3分子中N原子处在3个H原子所组成的三角形的中心
B. CCl4分子中C原子处在4个Cl原子所组成的正方形的中心
C. H2O分子中O原子不处在2个H原子所连成的直线的中央
D. CO2分子中C原子不处在2个O原子所连成的直线的中央
C
