江苏省徐州市东湖实验学校2022-2023学年九年级数学数学上册一元二次方程应用题练习(无答案)
文档属性
| 名称 | 江苏省徐州市东湖实验学校2022-2023学年九年级数学数学上册一元二次方程应用题练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 139.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 08:04:12 | ||
图片预览

文档简介
江苏省徐州市2022-2023学年度东湖实验学校九年级数学
一元二次方程应用题练习单1
一、单选题
1.建平县某中学九年级各班举行篮球比赛,每两个班之间都要赛一场,共赛10场,设共有x个班参赛,根据题意可列方程为( )
A. B. C. D.
2.九(1)班分到如图所示一块长为9m,宽为7m的矩形空地,计划在其中两块完全相同的矩形地种植蔬菜,它们的面积之和为,若人行道的宽度都为x,则可以列出关于x的方程( )
A. B.
C. D.
3.中考体育科目考试是对应届初中毕业生作出体质评价的统一测试.巴中市中考体育项目中有一项为一分钟跳绳,小明3月份的跳绳测试成绩为130个,经老师的指导和自己的努力,5月份的跳绳测试成绩为176个.设小明跳绳个数月平均增长率为x,则可列方程( )
A. B.
C. D.
4.为了迎接十一“黄金周”,某月季大观园准备分三个阶段扩大月季新品种种植面积,第一阶段已实现新品种的种植目标,第三阶段需实现的种植目标,设第二、第三阶段月季新品种种植面积的平均增长率为x,则下列方程正确的是( )
A. B.
C. D.
5.近年来,随着经济建设的蓬勃发展,鄂州市花大力气先后修成了江滩公园、西山公园、洋澜湖湿地公园、青天湖公园等各种主题公园,给广大市民提供了外出郊游的良好环境.据有关部门统计,2019年郊游人数约为20万人次,2021年郊游人数约为30万人次,设郊游人数年平均增长率为x,则下列方程中正确的是( )
A. B.
C. D.
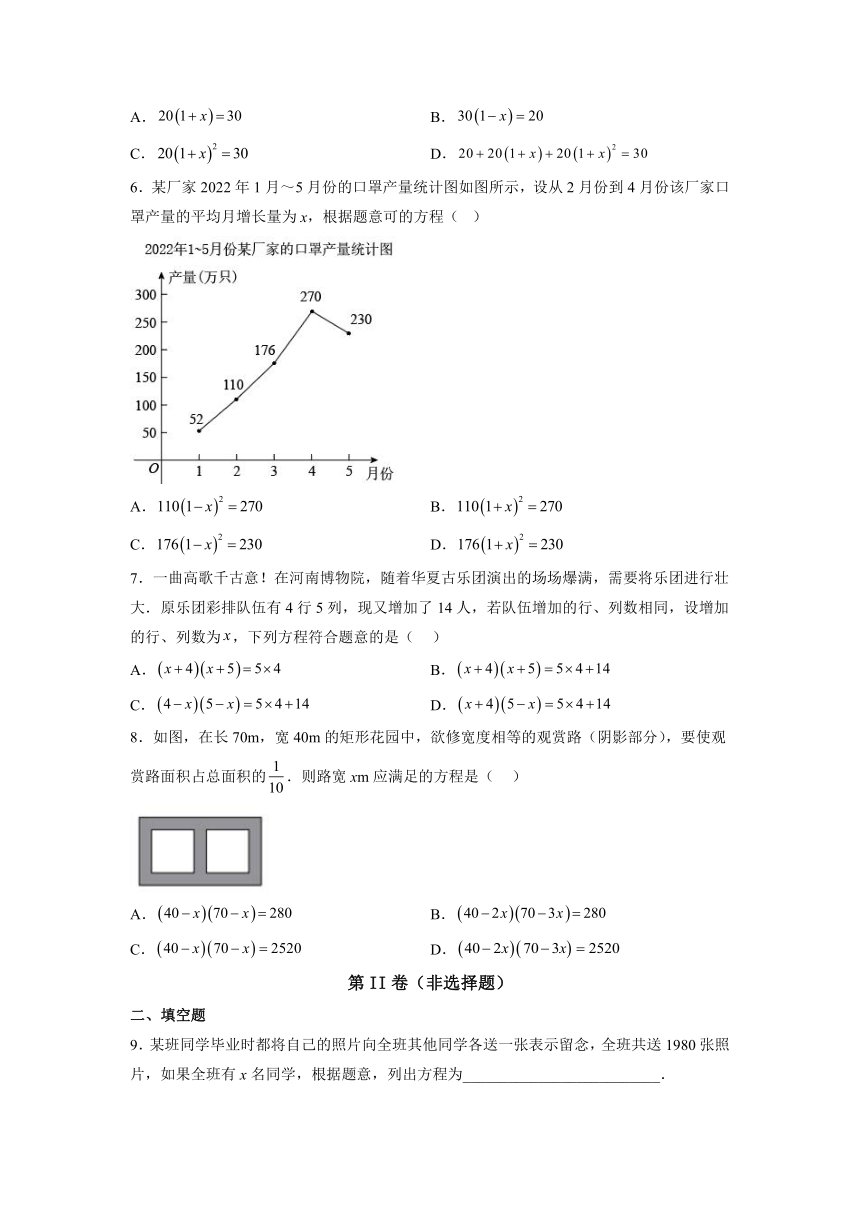
6.某厂家2022年1月~5月份的口罩产量统计图如图所示,设从2月份到4月份该厂家口罩产量的平均月增长量为x,根据题意可的方程( )
A. B.
C. D.
7.一曲高歌千古意!在河南博物院,随着华夏古乐团演出的场场爆满,需要将乐团进行壮大.原乐团彩排队伍有4行5列,现又增加了14人,若队伍增加的行、列数相同,设增加的行、列数为,下列方程符合题意的是( )
A. B.
C. D.
8.如图,在长70m,宽40m的矩形花园中,欲修宽度相等的观赏路(阴影部分),要使观赏路面积占总面积的.则路宽xm应满足的方程是( )
A. B.
C. D.
第II卷(非选择题)
二、填空题
9.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1980张照片,如果全班有x名同学,根据题意,列出方程为__________________________.
10.《长津湖》以抗美援朝战争中长津湖战役为背景,影片一上映就获得追捧,目前票房已突破亿.第二天票房为亿元,以后每天票房按相同的增长率增长,第四天的票房为亿元,若把增长率记作x.则方程可以列为________________________
11.近年来某市加大了对教育经费的投入,2018年投入2800万元,2020年将投入3900万元,该市投入教育经费的年平均增长率为,根据题意则可以列出的方程是________.
12.某中学准备在学校里利用米长的篱笆围成一个矩形花园,为充分利用材料,花园一面靠墙,要使得花园面积为,设垂直于墙的边长为xm,则可列方程为___________.
13.某读书小组在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了210本图书,如果设全组共有x名同学,依题意,可列出的方程是___________.
14.一种商品每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,则可列出方程 _____.
15.《田亩比类乘除捷法》中记载了一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步.”译文:一个矩形的面积为864平方步,宽比长少12步,问宽和长各多少步 设矩形的宽为步,由题意,可列方程为____________.
16.某工程队承包了一项污水处理工程,原计划每天铺设污水管道1250米,因准备工作不充分,第一天铺设了原计划的80%,从第二天开始,该工程队加快了铺设速度,第三天铺设了1440米.若该工程队第二天、第三天每天的铺设长度比前一天增长的百分数相同,设这个百分数为x,列出方程____________.
三、解答题
17.为了推进学校与社区融合发展,光明社区开通公众号进行免费线上公益直播授课,9月份该公众号关注人数为2万人,11月份该公众号关注人数达到万人.若从9月份到11月份,每月该公众号关注人数的平均增长率都相同,求该公众号关注人数的月平均增长率.
18.2022年2月4日,第24届冬季奥林匹克运动会在北京举行,吉祥物“冰墩墩”备受人民的喜爱,某商店经销吉祥物“冰墩墩”玩具,销售成本为每件40元,据市场分析,若按每件50元销售,一个月能售出500件.销售单价每涨1元,月销售量就减少10件.商店想使月销售利润能够达到8000元,且尽量减少库存,求销售单价应涨多少元?
19.如图,矩形绿地长,宽,要在这块绿地上修建宽度相同且与矩形各边垂直的三条道路,使六块绿地面积共,问道路宽应为多少?
20.百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.
(1)现在每件童装降价5元,那么每天可售出多少件,每天可盈利多少元?
(2)要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
21.中,,点P从点A开始沿边向终点B以1的速度移动,与此同时,点Q从点B开始沿边向终点C以2的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.
(1)填空______, ______(用含t的代数式表示);
(2)当t为何值时,的长度等于?
(3)是否存在t的值,使得的面积等于?若存在,请求出此时t的值;若不存在,请说明理由.
22.某图书店在2022年国庆节期间举行促销活动,某课外阅读书进货价为每本8元,标价为每本15元.
(1)该图书店举行了国庆大回馈活动,连续两次降价,每次降价的百分率相同,最后以每本9.6元的价格售出,求图书店每次降价的百分率;
(2)在九月底该书店老板去进货该书500本,按照(1)两次降价后的价格在国庆节全部售出;国庆节后老板去进货发现进货价上涨了,进货量比九月底增加,以标价的八折全部售出后,比国庆节的总利润多1200元,求的值.
一元二次方程应用题练习单1
一、单选题
1.建平县某中学九年级各班举行篮球比赛,每两个班之间都要赛一场,共赛10场,设共有x个班参赛,根据题意可列方程为( )
A. B. C. D.
2.九(1)班分到如图所示一块长为9m,宽为7m的矩形空地,计划在其中两块完全相同的矩形地种植蔬菜,它们的面积之和为,若人行道的宽度都为x,则可以列出关于x的方程( )
A. B.
C. D.
3.中考体育科目考试是对应届初中毕业生作出体质评价的统一测试.巴中市中考体育项目中有一项为一分钟跳绳,小明3月份的跳绳测试成绩为130个,经老师的指导和自己的努力,5月份的跳绳测试成绩为176个.设小明跳绳个数月平均增长率为x,则可列方程( )
A. B.
C. D.
4.为了迎接十一“黄金周”,某月季大观园准备分三个阶段扩大月季新品种种植面积,第一阶段已实现新品种的种植目标,第三阶段需实现的种植目标,设第二、第三阶段月季新品种种植面积的平均增长率为x,则下列方程正确的是( )
A. B.
C. D.
5.近年来,随着经济建设的蓬勃发展,鄂州市花大力气先后修成了江滩公园、西山公园、洋澜湖湿地公园、青天湖公园等各种主题公园,给广大市民提供了外出郊游的良好环境.据有关部门统计,2019年郊游人数约为20万人次,2021年郊游人数约为30万人次,设郊游人数年平均增长率为x,则下列方程中正确的是( )
A. B.
C. D.
6.某厂家2022年1月~5月份的口罩产量统计图如图所示,设从2月份到4月份该厂家口罩产量的平均月增长量为x,根据题意可的方程( )
A. B.
C. D.
7.一曲高歌千古意!在河南博物院,随着华夏古乐团演出的场场爆满,需要将乐团进行壮大.原乐团彩排队伍有4行5列,现又增加了14人,若队伍增加的行、列数相同,设增加的行、列数为,下列方程符合题意的是( )
A. B.
C. D.
8.如图,在长70m,宽40m的矩形花园中,欲修宽度相等的观赏路(阴影部分),要使观赏路面积占总面积的.则路宽xm应满足的方程是( )
A. B.
C. D.
第II卷(非选择题)
二、填空题
9.某班同学毕业时都将自己的照片向全班其他同学各送一张表示留念,全班共送1980张照片,如果全班有x名同学,根据题意,列出方程为__________________________.
10.《长津湖》以抗美援朝战争中长津湖战役为背景,影片一上映就获得追捧,目前票房已突破亿.第二天票房为亿元,以后每天票房按相同的增长率增长,第四天的票房为亿元,若把增长率记作x.则方程可以列为________________________
11.近年来某市加大了对教育经费的投入,2018年投入2800万元,2020年将投入3900万元,该市投入教育经费的年平均增长率为,根据题意则可以列出的方程是________.
12.某中学准备在学校里利用米长的篱笆围成一个矩形花园,为充分利用材料,花园一面靠墙,要使得花园面积为,设垂直于墙的边长为xm,则可列方程为___________.
13.某读书小组在学校举行的图书共享仪式上互赠图书,每个同学都把自己的图书向本组其他成员赠送一本,全组共互赠了210本图书,如果设全组共有x名同学,依题意,可列出的方程是___________.
14.一种商品每件售价为150元,经过连续两次降价后,该种商品每件售价为96元,设平均每次降价的百分率为x,则可列出方程 _____.
15.《田亩比类乘除捷法》中记载了一道题:“直田积八百六十四步,只云阔不及长一十二步,问阔及长各几步.”译文:一个矩形的面积为864平方步,宽比长少12步,问宽和长各多少步 设矩形的宽为步,由题意,可列方程为____________.
16.某工程队承包了一项污水处理工程,原计划每天铺设污水管道1250米,因准备工作不充分,第一天铺设了原计划的80%,从第二天开始,该工程队加快了铺设速度,第三天铺设了1440米.若该工程队第二天、第三天每天的铺设长度比前一天增长的百分数相同,设这个百分数为x,列出方程____________.
三、解答题
17.为了推进学校与社区融合发展,光明社区开通公众号进行免费线上公益直播授课,9月份该公众号关注人数为2万人,11月份该公众号关注人数达到万人.若从9月份到11月份,每月该公众号关注人数的平均增长率都相同,求该公众号关注人数的月平均增长率.
18.2022年2月4日,第24届冬季奥林匹克运动会在北京举行,吉祥物“冰墩墩”备受人民的喜爱,某商店经销吉祥物“冰墩墩”玩具,销售成本为每件40元,据市场分析,若按每件50元销售,一个月能售出500件.销售单价每涨1元,月销售量就减少10件.商店想使月销售利润能够达到8000元,且尽量减少库存,求销售单价应涨多少元?
19.如图,矩形绿地长,宽,要在这块绿地上修建宽度相同且与矩形各边垂直的三条道路,使六块绿地面积共,问道路宽应为多少?
20.百货商店服装柜在销售中发现:某品牌童装平均每天可售出20件,每件盈利40元.为了迎接“六一”国际儿童节,商场决定采取适当的降价措施.经市场调查发现:如果每件童装降价1元,那么平均每天就可多售出2件.
(1)现在每件童装降价5元,那么每天可售出多少件,每天可盈利多少元?
(2)要想平均每天销售这种童装盈利1200元,那么每件童装应降价多少元?
21.中,,点P从点A开始沿边向终点B以1的速度移动,与此同时,点Q从点B开始沿边向终点C以2的速度移动.如果P、Q分别从A、B同时出发,当点Q运动到点C时,两点停止运动.设运动时间为t秒.
(1)填空______, ______(用含t的代数式表示);
(2)当t为何值时,的长度等于?
(3)是否存在t的值,使得的面积等于?若存在,请求出此时t的值;若不存在,请说明理由.
22.某图书店在2022年国庆节期间举行促销活动,某课外阅读书进货价为每本8元,标价为每本15元.
(1)该图书店举行了国庆大回馈活动,连续两次降价,每次降价的百分率相同,最后以每本9.6元的价格售出,求图书店每次降价的百分率;
(2)在九月底该书店老板去进货该书500本,按照(1)两次降价后的价格在国庆节全部售出;国庆节后老板去进货发现进货价上涨了,进货量比九月底增加,以标价的八折全部售出后,比国庆节的总利润多1200元,求的值.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
