苏科版七年级上第5章走进图形世界全章课课练(无答案)[上学期]
文档属性
| 名称 | 苏科版七年级上第5章走进图形世界全章课课练(无答案)[上学期] | 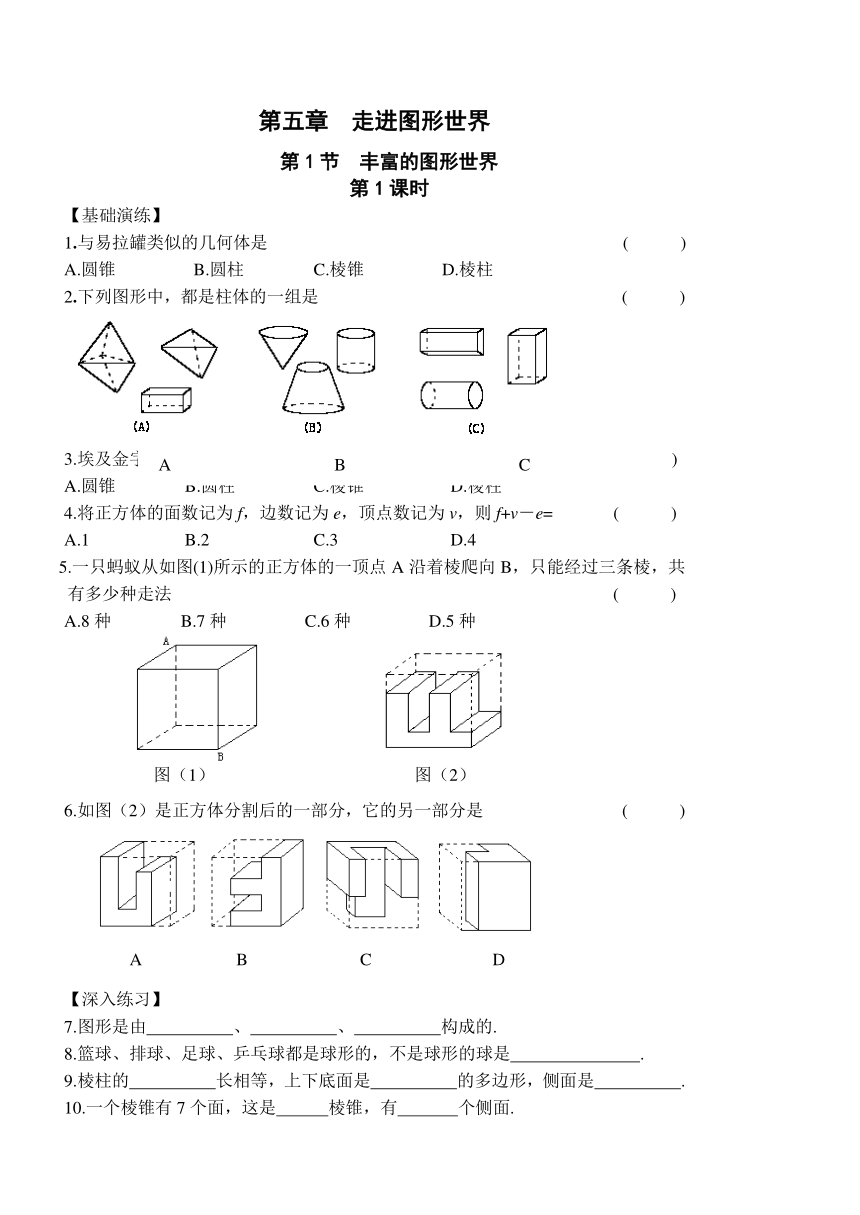 | |
| 格式 | rar | ||
| 文件大小 | 540.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-03 19:55:00 | ||
图片预览

文档简介
第五章 走进图形世界
第1节 丰富的图形世界
第1课时
【基础演练】
1.与易拉罐类似的几何体是 ( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
2.下列图形中,都是柱体的一组是 ( )
3.埃及金字塔类似于几何体 ( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
4.将正方体的面数记为f,边数记为e,顶点数记为v,则f+v-e= ( )
A.1 B.2 C.3 D.4
5.一只蚂蚁从如图(1)所示的正方体的一顶点A沿着棱爬向B,只能经过三条棱,共有多少种走法 ( )
A.8种 B.7种 C.6种 D.5种
6.如图(2)是正方体分割后的一部分,它的另一部分是 ( )
(B) (C) (D)
【深入练习】
7.图形是由 、 、 构成的.
8.篮球、排球、足球、乒乓球都是球形的,不是球形的球是 .
9.棱柱的 长相等,上下底面是 的多边形,侧面是 .
10.一个棱锥有7个面,这是 棱锥,有 个侧面.
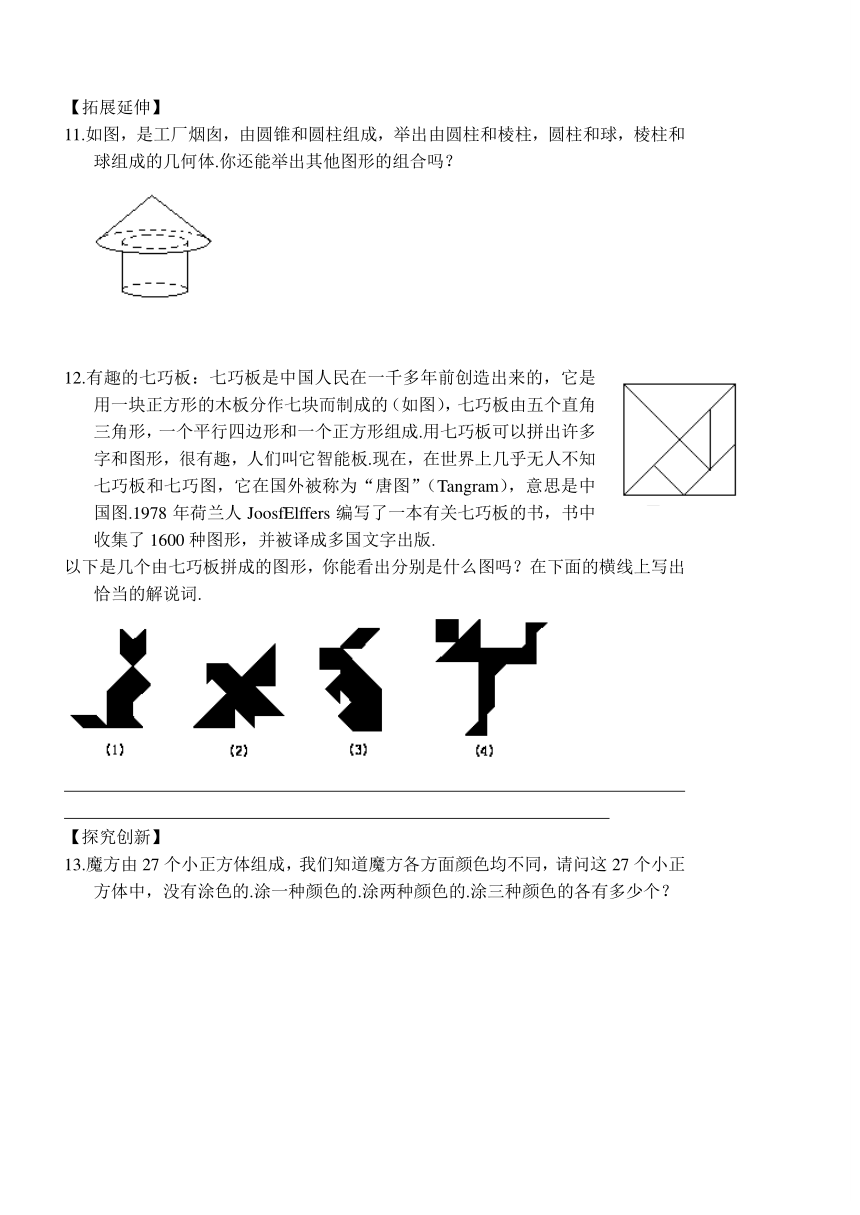
【拓展延伸】
11.如图,是工厂烟囱,由圆锥和圆柱组成,举出由圆柱和棱柱,圆柱和球,棱柱和球组成的几何体.你还能举出其他图形的组合吗?
12.有趣的七巧板:七巧板是中国人民在一千多年前创造出来的,它是用一块正方形的木板分作七块而制成的(如图),七巧板由五个直角三角形,一个平行四边形和一个正方形组成.用七巧板可以拼出许多字和图形,很有趣,人们叫它智能板.现在,在世界上几乎无人不知七巧板和七巧图,它在国外被称为“唐图”(Tangram),意思是中国图.1978年荷兰人JoosfElffers编写了一本有关七巧板的书,书中收集了1600种图形,并被译成多国文字出版.
以下是几个由七巧板拼成的图形,你能看出分别是什么图吗?在下面的横线上写出恰当的解说词.
【探究创新】
13.魔方由27个小正方体组成,我们知道魔方各方面颜色均不同,请问这27个小正方体中,没有涂色的.涂一种颜色的.涂两种颜色的.涂三种颜色的各有多少个?
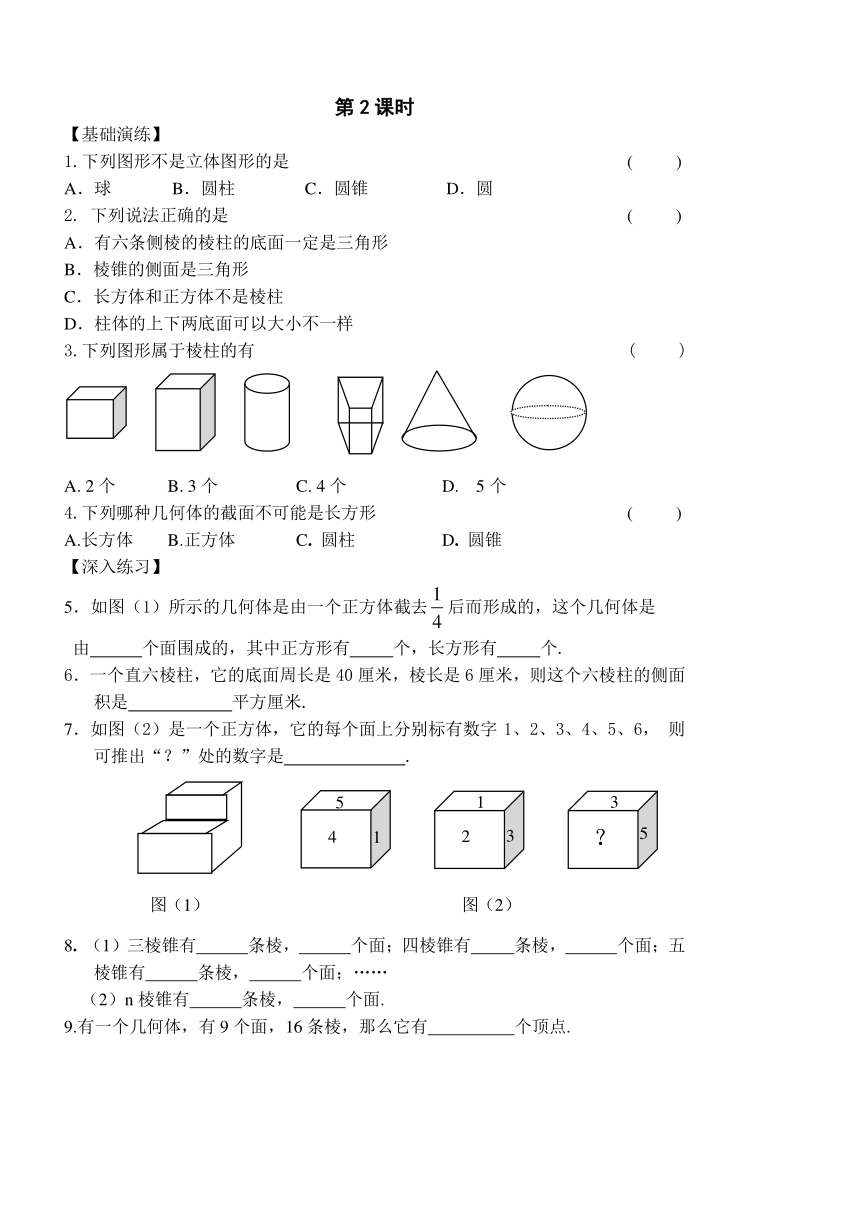
第2课时
【基础演练】
1.下列图形不是立体图形的是 ( )
A.球 B.圆柱 C.圆锥 D.圆
2. 下列说法正确的是 ( )
A.有六条侧棱的棱柱的底面一定是三角形
B.棱锥的侧面是三角形
C.长方体和正方体不是棱柱
D.柱体的上下两底面可以大小不一样
3.下列图形属于棱柱的有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
4.下列哪种几何体的截面不可能是长方形 ( )
A.长方体 B.正方体 C. 圆柱 D. 圆锥
【深入练习】
5.如图(1)所示的几何体是由一个正方体截去后而形成的,这个几何体是
由 个面围成的,其中正方形有 个,长方形有 个.
6.一个直六棱柱,它的底面周长是40厘米,棱长是6厘米,则这个六棱柱的侧面积是 平方厘米.
7.如图(2)是一个正方体,它的每个面上分别标有数字1、2、3、4、5、6, 则可推出“?”处的数字是 .
8. (1)三棱锥有 条棱, 个面;四棱锥有 条棱, 个面;五棱锥有 条棱, 个面;……
(2)n棱锥有 条棱, 个面.
9.有一个几何体,有9个面,16条棱,那么它有 个顶点.
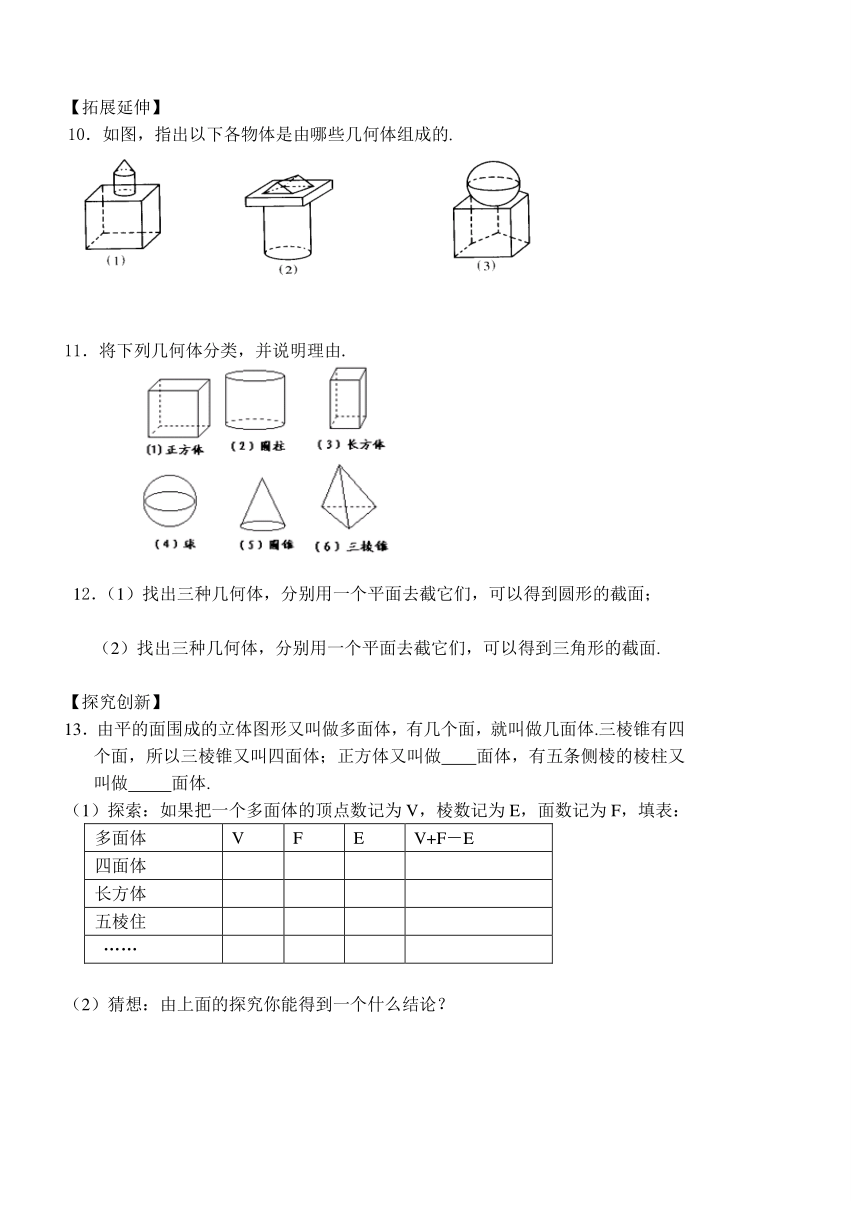
【拓展延伸】
10.如图,指出以下各物体是由哪些几何体组成的.
11.将下列几何体分类,并说明理由.
12.(1)找出三种几何体,分别用一个平面去截它们,可以得到圆形的截面;
(2)找出三种几何体,分别用一个平面去截它们,可以得到三角形的截面.
【探究创新】
13.由平的面围成的立体图形又叫做多面体,有几个面,就叫做几面体.三棱锥有四个面,所以三棱锥又叫四面体;正方体又叫做 面体,有五条侧棱的棱柱又叫做 面体.
(1)探索:如果把一个多面体的顶点数记为V,棱数记为E,面数记为F,填表:
多面体 V F E V+F-E
四面体
长方体
五棱住
……
(2)猜想:由上面的探究你能得到一个什么结论?
第五章 走进图形世界
5.2 图形的变化
第1课时
【基础演练】
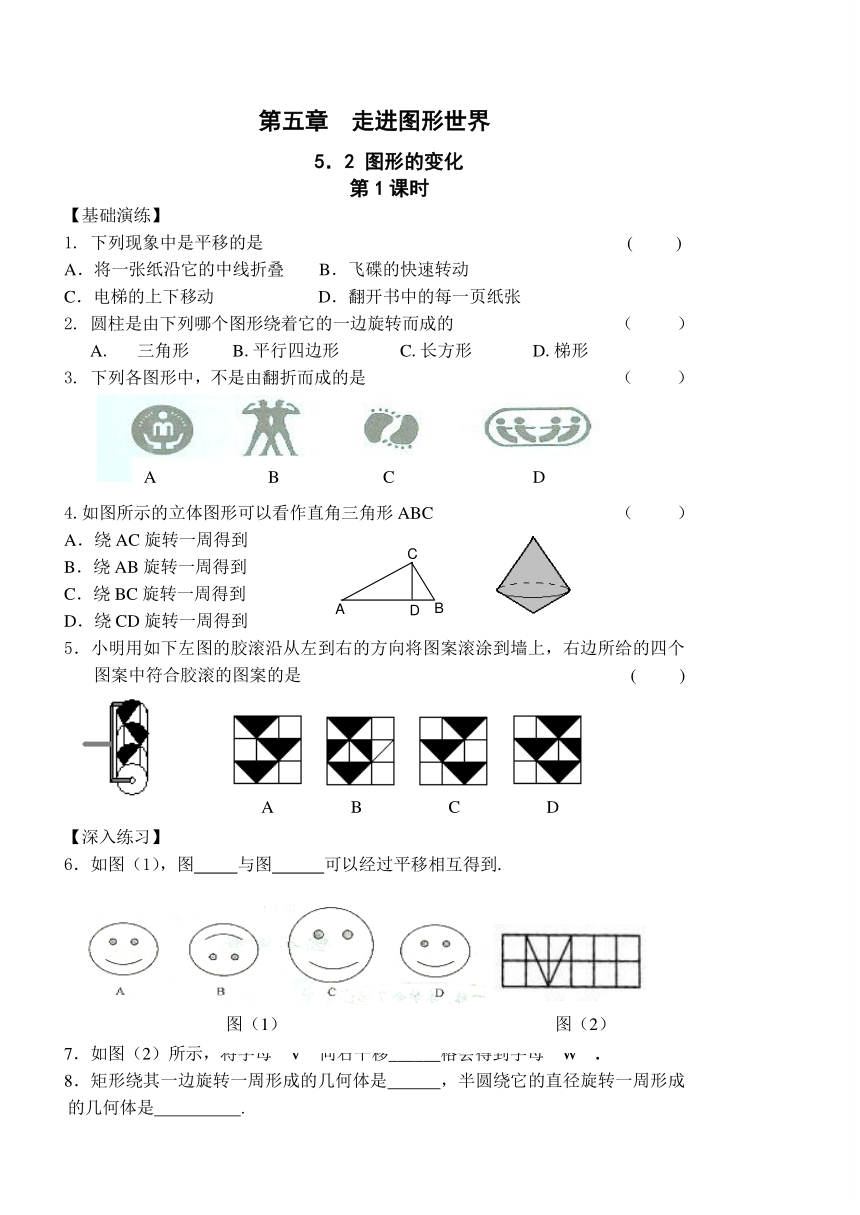
1. 下列现象中是平移的是 ( )
A.将一张纸沿它的中线折叠 B.飞碟的快速转动
C.电梯的上下移动 D.翻开书中的每一页纸张
2. 圆柱是由下列哪个图形绕着它的一边旋转而成的 ( )
A. 三角形 B.平行四边形 C.长方形 D.梯形
3. 下列各图形中,不是由翻折而成的是 ( )
4.如图所示的立体图形可以看作直角三角形ABC ( )
A.绕AC旋转一周得到
B.绕AB旋转一周得到
C.绕BC旋转一周得到
D.绕CD旋转一周得到
5.小明用如下左图的胶滚沿从左到右的方向将图案滚涂到墙上,右边所给的四个图案中符合胶滚的图案的是 ( )
【深入练习】
6.如图(1),图 与图 可以经过平移相互得到.
7.如图(2)所示,将字母“V”向右平移______格会得到字母“W”.
8.矩形绕其一边旋转一周形成的几何体是 ,半圆绕它的直径旋转一周形成的几何体是 .
9.以图中的虚线为对称轴,画出这些图形的另一半.(不写画法)
10.请你用一个三角形、一个圆、一条线段创造一个美丽的图案,并给图案加上恰当的解说词. (如右图铁锹)
【拓展延伸】
11.将以下方格中阴影图形围绕点O,按顺时针方向依次旋转90°,看看会得到什么图形?
12.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
【探究创新】
13.国庆节前,市园林部门准备在文化广场特设直径均为4米的八个圆形花坛,在花坛内放置面积相同的两种颜色的盆栽草花,要求各个花坛内两种草花的摆设不能相同,如下图中的①和②,请你再至少设计出四种方案.
第2课时
【基础演练】
1.观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是 ( )
2. 下列轴对称图形中,只有两条对称轴的图形是 ( )
3. 下列四个图形中,从几何图形的对称性考虑,与其他三个不同的是 ( )
4. 如图,下列黑体英文大写字母中既可以通过翻折变换.又可以通过旋转变换得到的图形是 ( )
? A.E B.M C.N D.H
5.如下图所示,将一圆形纸片对折后再对折,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是 ( )
【深入练习】
6.在如图所示的4个图形中,图形①与图形______成轴对称;图形______可以由图形①通过旋转变换得到; 图形______可以由图形①通过平移得到.(填写符合要求的图形所对应的序号).
7.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过,这一张牌是___________.
8.如图(3)可以看做是一个菱形通过______次旋转得到的,每次旋转______ 度.
【拓展延伸】
9.如图所示,按要求涂色:
(1)将图形A平移到图形B;
(2)将图形B沿图中虚线翻折到图形C;
(3)将图形C沿其右下方的顶点旋转180°到图形D.
10.画出下列图形的对称轴.
【探究创新】
11.下面各图都是只有一条对称轴的图形,请你涂黑图形的一部分,使它成为具有两条或两条以上对称轴的图形.
第五章 走进图形世界
第2节 展开与折叠
第1课时
【基础演练】
1.圆锥的侧面展开图是 ( )
A.长方形 B. 正方形 C. 圆 D. 扇形
2.下列说法中正确的是 ( )
A. 正方体是四面体 B. 长方体是四棱柱,四棱柱是长方体
C 棱锥的底面一定是四边形. D. 圆柱的侧面展开图是长方形
3.在下列图形中(每个小正方形都是相同的正方形),是正方体的表面
展开图的是 ( )
A B C D
4. 一个正方体,六个面上分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图(1)所示,你能看到的数为7、10、11,则六个整数的和为 ( )
A.51 B.52 C.57 D.58
5. 如图(2), 已知正方体的各个侧面分别标上字母a,b,c,d,e,f;其中a在后面,b在下面,c在左面,则下列结论错误的是 ( )
A、d在上面 B、e在前面 C、f在右面 D、d在前面
【深入练习】
6.一个长方体的长、宽、高分别是3厘米、4厘米、5厘米,则它的表面积是 cm2.
7. 将一张弧长为20π厘米的扇形纸片卷成一个圆锥模型的侧面,这个圆锥底面圆的半
径是 厘米.
8.若要使如图(3)所示的平面展开图折叠成正方体后,相对面上两个数之和为6,则x=_______,y=______.
9.如图(4)是一多面体的外表面展开图形,每个面都标有字母,请根据要求回答提问:
(1)如果面A在多面体的底部,那么面 在上面.
(2)如果面F在前面,从左面看是面B,则面 在上面.
(3)从右面看是面C,面D在后面,面 在上面.
【拓展延伸】
10.想一想:若将图中这个无底的立体图形剪开,会是怎样的平面图形?请你将示意图画出来.
11.如图所示图是长方体的表面展开图,折叠成一个长方体,那么与字母 J重合的点是哪几个?
12、如图某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图上阴影部分),但是一不小心,少画了一个,请你给他补上一个,可以组合成正方体,你有几种画法,在图上用阴影注明.
【探究创新】
13、如图是一个圆锥的展开图,其中小圆是圆锥的底面,半圆的直径的两个端点是A、B,开始时小圆上一点P与点A重合,当这个小圆紧贴半圆滚动一周后,你会发现什么现象?由此你发现半圆的直径与小圆的直径有什么关系?
第2课时
【基础演练】
1. 如图(1)个三角形都是等边三角形,将图形折叠,得到的立体图形是 ( )
A.三棱锥 B.圆锥体
C.棱锥体 D.六面体
2. 下列图形中,哪一个是四棱柱的侧面展开图 ( )
3. 下列各个平面图形中,属于圆锥的平面展开图的是 ( )
A B C D
4. 如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别是 ( )
A.蓝、绿、黑 B.绿、蓝、黑 C.绿、黑、蓝 D.蓝、黑、绿
5.如图所示的立方体,如果把它展开,可以是下列图形中的 ( )
A B C D
【深入练习】
6.一个正方体的平面展开图如图(1)所示,则正方形4的对面是正方形 .
7.已知一不透明的正方体的六个面上分别写着1至6六个数字,如图(2)是我们能看到的三种情况,那么1和5的对面数字分别是____和_____.
【拓展延伸】
8.下列图形都是某些几何体的平面展开图,在对应图形下面的横线上填写几何体的名称.
__________ __________ __________ __________
9.一个正方体的骰子,1和6,2和5,3和4是分别相对的面上的点.现在有12个正方形格子的纸上画好了点状的图案,如图所示,若要经过折叠能做成一个骰子,你认为应剪掉哪6个正方形格子?(请用笔在要剪掉的正方形格子上打“×”,不必写理由)
10.给出两个等边三角形纸片如图,要求用其中一个剪成底面是等边三角形的三棱锥,另一个剪成上下底面是等边三角形的直三棱柱.请你设计一种剪拼的方法,分别在图上用虚线画出来.
【探究创新】
11.一只蜘蛛在一个正方体的顶点A处,一只蚊子在正方体的顶点B出,如图3.3-7所示,现在蜘蛛想尽快地捉到这只蚊子,那么它所走的最短路线是怎样的,在图上画出来,这样的最短路线有几条(通过画展开图说明)
第五章 走进图形世界
第3节 从三个方向看
第1课时
【基础演练】
1.从三个方向观察同一个物体,可能看到不同的图形,简称三视图,下列选项不在三视图之列的是 ( )
A.主视图 B.右视图 C.左视图 D.俯视图
2. 一个直立在水平面上的圆柱体的主视图、俯视图、左视图分别是 ( )
A. 圆、长方形、长方形 B.长方形、长方形、圆
C. 长方形、圆、长方形 D.长方形、圆、圆
3.若一个立体图形的主视图与左视图都是等腰三角形,俯视图是圆,则这个图形可能是 ( )
A.圆台 B.圆柱 C.圆锥 D.三棱锥
4.下列平面图形中,哪一个是右边几何体的左视图 ( )
A B C D
5.有9个小方块堆成如图所示的几何体,这个几何体表面包含小方块表面的数目是 ( )
A.32 B.30 C.22 D.20.
【深入练习】
6. 如图所示,电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面,则A图象是______号摄像机所拍,B图象是______号摄像机所拍,C图象是______号摄像机所拍,D图象是______号摄像机所拍.
7. 指出左边三个平面图形是右边这个物体的三视图中的哪个视图.
8.一物体的三视图如下图,你能描述该物体的形状吗?
【拓展延伸】
9.已知:如图,一个平面截正方体,得到一个四边形截面,试分别画出这个截面在这个正方体的三视图中的位置.
10.下图是由五块积木搭成,这几块积木都是相同的正方体,请画出这个图形的主视图、左视图和俯视图.
11.画出如图所示的螺帽的三视图.
【探究创新】
12. 大小两个正方体叠成如图所示几何体,请作出它的三视图.
第2课时
【基础演练】
1.某一物体的三视图如右:那么这个物体应该是 ( )
2. 从不同方向观察如图所示的几何体,不可能看到的是 ( )
A B C D
3. 由五个正方体搭成的几何体的俯视图如图所示,则物体的主视图不可能是 ( )
俯视图 A B C D
4.如图是一个立体图形的三视图,这个图形是由一些相同的小正方体搭成的,这些小正方体的个数是 ( )
A.6 B.7 C.8 D.9
【深入练习】
5.举出三视图形状都一样的几何体两个:_______、_________.
6.举出两个主视图和左视图都为矩形的例子:__________、__________.
7.根据下列物体的三视图,填出几何体的名称(或画出图形)
主视图 俯视图 左视图 几何体是_____
主视图 俯视图 左视图 几何体是_____
8.在桌上摆有一些大小相同的正方体木块,主视图.左视图如图,要摆出这样的图形至少需要 块正方体木块,至多需要 块正方体木块.
【拓展延伸】
9.如图是一个有若干个小正方体搭成的几何体的俯视图,其中小正方形格内的数字是小正方体的层数,请你画出它的主视图和左视图.
10.在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要核实一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据图中的三视图,帮他清点一下箱子的数量吗?
【探究创新】
11.已知下图为一几何体的三视图:(1)写出这个几何体的名称;(2)任意画出它的一种表面展开图;(3)若主视图的长为10,俯视图中三角形的边长为4,求这个几何体的侧面积.
第五章 走进图形世界
第4节 数学活动——制作礼品盒
第1课时
【基础演练】
1.如图是一个长方体的展开图,如果将它折叠起来,其中点G与点 重合,点L与点 和点 重合.
2.如图,有一个6×6正方形格纸,在四个角各剪去一个1×1的正方形,然后折叠成一个无盖长方体纸盒,求其容积.
3.如果上题中,在四个角各剪去一个2×2的正方形,折叠成一个无盖长方体纸盒,求其容积.
4.问题:用一张边长6cm的正方形纸片制作一个无盖的长方体纸盒,应该怎样制作?怎样制作使得容积较大呢?试给出三种制作方法,并比较制成的纸盒的容积的大小?
【拓展延伸】
1.右图是一多面体的展开图,每个面内都标注了字母,请根据要求回答下列问题:
⑴如果面A在多面体的底部,那么面_______会在上面.
⑵如果面F在前面,从左面看是面B,那么面_______
会在上面.
⑶如果从右面看是面C,面D在后面,那么面_______
会在上面.
2.如果一个长方体的三视图的面积分别为6cm2.3cm2.2cm2,那么这个长方体的体积为__________cm3.
3.骰子是一个正方体,它的相对两个面上的点数之和相等.请在右图中的4×3方格内选择6个相连的正方形,使它们作为一个整体能折成一个骰子的侧面.
(请在图中画出选中部分的轮廓)
4.一种香皂,每一块的长.宽.高分别为16cm.6cm.3cm,现需给这种香皂设计一种包装盒,要求如下:
①每盒装香皂30块;
②香皂相同的面相互对接(外侧的面除外);
③装入香皂后盒内不留空隙;
④包装盒是一个长方体.
⑴根据要求,你一定能设计多种规格的包装盒。请动手试一试,动笔算一算,你认为哪种设计方案最省料?
⑵画出按最省料方案制作的一个包装盒的三视图,计算每一个这样的包装盒需用包装纸多少cm2?(接头粘合部分忽略不计)
第五章 走进图形世界
单元复习小结
一.精心选一选:
1.下面图形是棱柱的是 ( )
A B C D
2.下列图形中,是正方体的平面展开图的是 ( )
A B C D
3.已知某多面体的平面展开图如图所示,其中是三棱柱的有 ( )
A.1个 B.2个 C.3个 D.4个
4.圆锥的侧面展开图是 ( )
A.长方形 B.正方形 C.圆 D.扇形
5.下列交通标志图中,属于轴对称图形的是 ( )
6.如图的陀螺是由下面哪两个几何体组合而成的 ( )
A.长方体和圆锥 B.长方体和三角形
C.圆和三角形 D.圆柱和圆锥
7.如果有一个正方体,它的展开图可能是下面四个展开图中的 ( )
二.细心填一填:
8.长方体有 个面, 条棱, 个顶点.
9.半圆面绕直径旋转一周形成 .
10.一个几何体的三视图是两个同样大小的长方形和一个直径等于长方形一边长的圆,这个几何体是 .
三.努力用一用:
11.如图,是由几个小立方块搭成的几何体的俯视图,小正方形的数字表示该位置小立方块的个数,请画出相应的几何体的主视图及左视图.
12.一个正方体所有相对的面上两数之和相等.下图是它的展开图,请填好图中空白正方形中的数.
13.画出下列几何体的三视图.
第五章达标测试卷
一.精心选一选(每题3分,共计30分)
1.下列立体图形,属于多面体的是 ( )
A.圆柱 B.长方体 C.球 D.圆锥
2.圆柱可以看作由下列哪个图形沿它的一边快速旋转得到 ( )
A.直角三角形 B.梯形 C.长方形 D.等腰三角形
3.两个完全相同的正方体,将一面完全重合,构成的几何体面数有 ( )
A.12个 B.11个 C.10个 D.6个
4.将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到 ( )
A B C D
5.一个立体图形的三视图形如图所示,则该立体图形是 ( )
主视图 左视图 俯视图
A.圆锥 B.球 C.圆柱 D.圆
6.下面图形不能围成一个长方体的是 ( )
7.4张扑克牌如图⑴所示放在桌上,小敏把其中一张旋转180°后得到如图⑵所示,那么她所旋转的牌从左数起是 ( )
A.第一张 B.第二张 C.第三张 D.第四张
8.左图是正方体的表面展开图,如果将其合成原来的正方体(如图)时,与点P重合的两点应该是 ( )
A.S和Z B.T和Y C.U和Y D.T和V
9.将一个正方体沿着某些棱剪开,展成一个平面图形,至少需要剪的棱的条数是 ( )
A.5条 B.6条 C.7条 D.8条
10.有一块正方体木块,它的六个面上分别标上数字1~6,下图是这个正方体木块从不同面所看到的数字情况,请问5对面的数字是 ( )
A.3 B.4 C.6 D.无法确定
二.细心填一填(每题3分,共计24分)
11.如图中的图形2可以看作图形1向下平移 格,再向左平移 格得到.
12.如果某几何体它的俯视图.主视图及左视图都相同,则该几何体可能是 .
13.圆锥的侧面展开图是 形.
14.圆柱由 个面围成,其中 个平面, 个曲面.
15.如图,沿正三角形三边中点连线折起,可拼得一个 .
(第11题图) (第15题图)
16.桌面上放着一个三棱锥和一个圆柱体(如左图),在右图中填上它的视图的名称:
视图 视图 视图
17举出俯视图是圆的三个不同物体的例子:_____._____.______.
18一辆汽车从小明的面前经过,小明拍摄了一组照片.若按照汽车被摄入镜头的先后顺序给下面的照片编号为 .
三.努力用一用(共计46分)
19(4分).如图中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.
20(8分).如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图与左视图.
21(6分).如下是七种图形:圆 、线段、 正方形 、长方形、 三角形 、五边形 、六边形
请你选用这七种图形中的若干种(不少于两种)构造一幅图案,并用一句话说明你构想的是什么,例如右图就是符合要求的一个图案.请你在下边构造出两个与之不同的图案,并加以说明.
一辆汽车
22(6分).已知:图(1).图(2)分别是6×6正方形网格上两个轴对称图形(阴影部分),其面积分别为SA.SB(网格中最小的正方形面积为一个平方单位),请观察图形并解答下列问题.
(1)填空:SA∶SB的值是 ;
(2)请你在图(3)的网格上画出一个面积为8个平方单位的图形,要求图形可以看作由其中的一个基本图形经过平移.翻折或旋转形成的.
23(6分).在规格为6×6的正方形网格中,有一个L形图案(如图所示的阴影部分).请你用三种不同的方法分别在下图中再将一个空白的小正方形涂成阴影,使整个阴影部分成为轴对称图形.
24(6分).如图所示,在正方体能见到的面上写上数1.2.3,而在展开图中也已分别写上了两个和一个指定的数.请你在展开图的其它各面上写上适当的数,使得相对的面上两数的和等于7.
25(10分).用一个小立方块搭一个几何体,它的主视图和俯视图如图所示,尝试画出所有可能的左视图.想一想,搭成这个几何体最少需要多少个小立方块?最多需要多少个小立方块?
A B C
图(2)
图(1)
A B C D
图(1)
1
5
2
5
3
4
1
3
?
图(2)
走
A B C D
A B C D
图(1) 图(2)
铁锹
(3)
图(2)
图(1)
图(3)
图(4)
A B C D
图(1)
图(2)
主视图
左视图
俯视图
A
B
C
D
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
图(1)
A B C D
第1节 丰富的图形世界
第1课时
【基础演练】
1.与易拉罐类似的几何体是 ( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
2.下列图形中,都是柱体的一组是 ( )
3.埃及金字塔类似于几何体 ( )
A.圆锥 B.圆柱 C.棱锥 D.棱柱
4.将正方体的面数记为f,边数记为e,顶点数记为v,则f+v-e= ( )
A.1 B.2 C.3 D.4
5.一只蚂蚁从如图(1)所示的正方体的一顶点A沿着棱爬向B,只能经过三条棱,共有多少种走法 ( )
A.8种 B.7种 C.6种 D.5种
6.如图(2)是正方体分割后的一部分,它的另一部分是 ( )
(B) (C) (D)
【深入练习】
7.图形是由 、 、 构成的.
8.篮球、排球、足球、乒乓球都是球形的,不是球形的球是 .
9.棱柱的 长相等,上下底面是 的多边形,侧面是 .
10.一个棱锥有7个面,这是 棱锥,有 个侧面.
【拓展延伸】
11.如图,是工厂烟囱,由圆锥和圆柱组成,举出由圆柱和棱柱,圆柱和球,棱柱和球组成的几何体.你还能举出其他图形的组合吗?
12.有趣的七巧板:七巧板是中国人民在一千多年前创造出来的,它是用一块正方形的木板分作七块而制成的(如图),七巧板由五个直角三角形,一个平行四边形和一个正方形组成.用七巧板可以拼出许多字和图形,很有趣,人们叫它智能板.现在,在世界上几乎无人不知七巧板和七巧图,它在国外被称为“唐图”(Tangram),意思是中国图.1978年荷兰人JoosfElffers编写了一本有关七巧板的书,书中收集了1600种图形,并被译成多国文字出版.
以下是几个由七巧板拼成的图形,你能看出分别是什么图吗?在下面的横线上写出恰当的解说词.
【探究创新】
13.魔方由27个小正方体组成,我们知道魔方各方面颜色均不同,请问这27个小正方体中,没有涂色的.涂一种颜色的.涂两种颜色的.涂三种颜色的各有多少个?
第2课时
【基础演练】
1.下列图形不是立体图形的是 ( )
A.球 B.圆柱 C.圆锥 D.圆
2. 下列说法正确的是 ( )
A.有六条侧棱的棱柱的底面一定是三角形
B.棱锥的侧面是三角形
C.长方体和正方体不是棱柱
D.柱体的上下两底面可以大小不一样
3.下列图形属于棱柱的有 ( )
A. 2个 B. 3个 C. 4个 D. 5个
4.下列哪种几何体的截面不可能是长方形 ( )
A.长方体 B.正方体 C. 圆柱 D. 圆锥
【深入练习】
5.如图(1)所示的几何体是由一个正方体截去后而形成的,这个几何体是
由 个面围成的,其中正方形有 个,长方形有 个.
6.一个直六棱柱,它的底面周长是40厘米,棱长是6厘米,则这个六棱柱的侧面积是 平方厘米.
7.如图(2)是一个正方体,它的每个面上分别标有数字1、2、3、4、5、6, 则可推出“?”处的数字是 .
8. (1)三棱锥有 条棱, 个面;四棱锥有 条棱, 个面;五棱锥有 条棱, 个面;……
(2)n棱锥有 条棱, 个面.
9.有一个几何体,有9个面,16条棱,那么它有 个顶点.
【拓展延伸】
10.如图,指出以下各物体是由哪些几何体组成的.
11.将下列几何体分类,并说明理由.
12.(1)找出三种几何体,分别用一个平面去截它们,可以得到圆形的截面;
(2)找出三种几何体,分别用一个平面去截它们,可以得到三角形的截面.
【探究创新】
13.由平的面围成的立体图形又叫做多面体,有几个面,就叫做几面体.三棱锥有四个面,所以三棱锥又叫四面体;正方体又叫做 面体,有五条侧棱的棱柱又叫做 面体.
(1)探索:如果把一个多面体的顶点数记为V,棱数记为E,面数记为F,填表:
多面体 V F E V+F-E
四面体
长方体
五棱住
……
(2)猜想:由上面的探究你能得到一个什么结论?
第五章 走进图形世界
5.2 图形的变化
第1课时
【基础演练】
1. 下列现象中是平移的是 ( )
A.将一张纸沿它的中线折叠 B.飞碟的快速转动
C.电梯的上下移动 D.翻开书中的每一页纸张
2. 圆柱是由下列哪个图形绕着它的一边旋转而成的 ( )
A. 三角形 B.平行四边形 C.长方形 D.梯形
3. 下列各图形中,不是由翻折而成的是 ( )
4.如图所示的立体图形可以看作直角三角形ABC ( )
A.绕AC旋转一周得到
B.绕AB旋转一周得到
C.绕BC旋转一周得到
D.绕CD旋转一周得到
5.小明用如下左图的胶滚沿从左到右的方向将图案滚涂到墙上,右边所给的四个图案中符合胶滚的图案的是 ( )
【深入练习】
6.如图(1),图 与图 可以经过平移相互得到.
7.如图(2)所示,将字母“V”向右平移______格会得到字母“W”.
8.矩形绕其一边旋转一周形成的几何体是 ,半圆绕它的直径旋转一周形成的几何体是 .
9.以图中的虚线为对称轴,画出这些图形的另一半.(不写画法)
10.请你用一个三角形、一个圆、一条线段创造一个美丽的图案,并给图案加上恰当的解说词. (如右图铁锹)
【拓展延伸】
11.将以下方格中阴影图形围绕点O,按顺时针方向依次旋转90°,看看会得到什么图形?
12.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?
【探究创新】
13.国庆节前,市园林部门准备在文化广场特设直径均为4米的八个圆形花坛,在花坛内放置面积相同的两种颜色的盆栽草花,要求各个花坛内两种草花的摆设不能相同,如下图中的①和②,请你再至少设计出四种方案.
第2课时
【基础演练】
1.观察下面图案,在A、B、C、D四幅图案中,能通过图案(1)的平移得到的是 ( )
2. 下列轴对称图形中,只有两条对称轴的图形是 ( )
3. 下列四个图形中,从几何图形的对称性考虑,与其他三个不同的是 ( )
4. 如图,下列黑体英文大写字母中既可以通过翻折变换.又可以通过旋转变换得到的图形是 ( )
? A.E B.M C.N D.H
5.如下图所示,将一圆形纸片对折后再对折,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是 ( )
【深入练习】
6.在如图所示的4个图形中,图形①与图形______成轴对称;图形______可以由图形①通过旋转变换得到; 图形______可以由图形①通过平移得到.(填写符合要求的图形所对应的序号).
7.如图(1)所示,魔术师把4张扑克牌放在桌子上,然后蒙住眼睛,请一位观众上台,把某一张牌旋转180.魔术师解除蒙具后,看到4张扑克牌如图(2)所示,他很快确定了哪一张牌被旋转过,这一张牌是___________.
8.如图(3)可以看做是一个菱形通过______次旋转得到的,每次旋转______ 度.
【拓展延伸】
9.如图所示,按要求涂色:
(1)将图形A平移到图形B;
(2)将图形B沿图中虚线翻折到图形C;
(3)将图形C沿其右下方的顶点旋转180°到图形D.
10.画出下列图形的对称轴.
【探究创新】
11.下面各图都是只有一条对称轴的图形,请你涂黑图形的一部分,使它成为具有两条或两条以上对称轴的图形.
第五章 走进图形世界
第2节 展开与折叠
第1课时
【基础演练】
1.圆锥的侧面展开图是 ( )
A.长方形 B. 正方形 C. 圆 D. 扇形
2.下列说法中正确的是 ( )
A. 正方体是四面体 B. 长方体是四棱柱,四棱柱是长方体
C 棱锥的底面一定是四边形. D. 圆柱的侧面展开图是长方形
3.在下列图形中(每个小正方形都是相同的正方形),是正方体的表面
展开图的是 ( )
A B C D
4. 一个正方体,六个面上分别写着六个连续的整数,且每个相对面上的两个数之和相等,如图(1)所示,你能看到的数为7、10、11,则六个整数的和为 ( )
A.51 B.52 C.57 D.58
5. 如图(2), 已知正方体的各个侧面分别标上字母a,b,c,d,e,f;其中a在后面,b在下面,c在左面,则下列结论错误的是 ( )
A、d在上面 B、e在前面 C、f在右面 D、d在前面
【深入练习】
6.一个长方体的长、宽、高分别是3厘米、4厘米、5厘米,则它的表面积是 cm2.
7. 将一张弧长为20π厘米的扇形纸片卷成一个圆锥模型的侧面,这个圆锥底面圆的半
径是 厘米.
8.若要使如图(3)所示的平面展开图折叠成正方体后,相对面上两个数之和为6,则x=_______,y=______.
9.如图(4)是一多面体的外表面展开图形,每个面都标有字母,请根据要求回答提问:
(1)如果面A在多面体的底部,那么面 在上面.
(2)如果面F在前面,从左面看是面B,则面 在上面.
(3)从右面看是面C,面D在后面,面 在上面.
【拓展延伸】
10.想一想:若将图中这个无底的立体图形剪开,会是怎样的平面图形?请你将示意图画出来.
11.如图所示图是长方体的表面展开图,折叠成一个长方体,那么与字母 J重合的点是哪几个?
12、如图某同学在制作正方体模型的时候,在方格纸上画出几个小正方形(图上阴影部分),但是一不小心,少画了一个,请你给他补上一个,可以组合成正方体,你有几种画法,在图上用阴影注明.
【探究创新】
13、如图是一个圆锥的展开图,其中小圆是圆锥的底面,半圆的直径的两个端点是A、B,开始时小圆上一点P与点A重合,当这个小圆紧贴半圆滚动一周后,你会发现什么现象?由此你发现半圆的直径与小圆的直径有什么关系?
第2课时
【基础演练】
1. 如图(1)个三角形都是等边三角形,将图形折叠,得到的立体图形是 ( )
A.三棱锥 B.圆锥体
C.棱锥体 D.六面体
2. 下列图形中,哪一个是四棱柱的侧面展开图 ( )
3. 下列各个平面图形中,属于圆锥的平面展开图的是 ( )
A B C D
4. 如图,下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色,那么涂黄色、白色、红色的对面分别是 ( )
A.蓝、绿、黑 B.绿、蓝、黑 C.绿、黑、蓝 D.蓝、黑、绿
5.如图所示的立方体,如果把它展开,可以是下列图形中的 ( )
A B C D
【深入练习】
6.一个正方体的平面展开图如图(1)所示,则正方形4的对面是正方形 .
7.已知一不透明的正方体的六个面上分别写着1至6六个数字,如图(2)是我们能看到的三种情况,那么1和5的对面数字分别是____和_____.
【拓展延伸】
8.下列图形都是某些几何体的平面展开图,在对应图形下面的横线上填写几何体的名称.
__________ __________ __________ __________
9.一个正方体的骰子,1和6,2和5,3和4是分别相对的面上的点.现在有12个正方形格子的纸上画好了点状的图案,如图所示,若要经过折叠能做成一个骰子,你认为应剪掉哪6个正方形格子?(请用笔在要剪掉的正方形格子上打“×”,不必写理由)
10.给出两个等边三角形纸片如图,要求用其中一个剪成底面是等边三角形的三棱锥,另一个剪成上下底面是等边三角形的直三棱柱.请你设计一种剪拼的方法,分别在图上用虚线画出来.
【探究创新】
11.一只蜘蛛在一个正方体的顶点A处,一只蚊子在正方体的顶点B出,如图3.3-7所示,现在蜘蛛想尽快地捉到这只蚊子,那么它所走的最短路线是怎样的,在图上画出来,这样的最短路线有几条(通过画展开图说明)
第五章 走进图形世界
第3节 从三个方向看
第1课时
【基础演练】
1.从三个方向观察同一个物体,可能看到不同的图形,简称三视图,下列选项不在三视图之列的是 ( )
A.主视图 B.右视图 C.左视图 D.俯视图
2. 一个直立在水平面上的圆柱体的主视图、俯视图、左视图分别是 ( )
A. 圆、长方形、长方形 B.长方形、长方形、圆
C. 长方形、圆、长方形 D.长方形、圆、圆
3.若一个立体图形的主视图与左视图都是等腰三角形,俯视图是圆,则这个图形可能是 ( )
A.圆台 B.圆柱 C.圆锥 D.三棱锥
4.下列平面图形中,哪一个是右边几何体的左视图 ( )
A B C D
5.有9个小方块堆成如图所示的几何体,这个几何体表面包含小方块表面的数目是 ( )
A.32 B.30 C.22 D.20.
【深入练习】
6. 如图所示,电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面,则A图象是______号摄像机所拍,B图象是______号摄像机所拍,C图象是______号摄像机所拍,D图象是______号摄像机所拍.
7. 指出左边三个平面图形是右边这个物体的三视图中的哪个视图.
8.一物体的三视图如下图,你能描述该物体的形状吗?
【拓展延伸】
9.已知:如图,一个平面截正方体,得到一个四边形截面,试分别画出这个截面在这个正方体的三视图中的位置.
10.下图是由五块积木搭成,这几块积木都是相同的正方体,请画出这个图形的主视图、左视图和俯视图.
11.画出如图所示的螺帽的三视图.
【探究创新】
12. 大小两个正方体叠成如图所示几何体,请作出它的三视图.
第2课时
【基础演练】
1.某一物体的三视图如右:那么这个物体应该是 ( )
2. 从不同方向观察如图所示的几何体,不可能看到的是 ( )
A B C D
3. 由五个正方体搭成的几何体的俯视图如图所示,则物体的主视图不可能是 ( )
俯视图 A B C D
4.如图是一个立体图形的三视图,这个图形是由一些相同的小正方体搭成的,这些小正方体的个数是 ( )
A.6 B.7 C.8 D.9
【深入练习】
5.举出三视图形状都一样的几何体两个:_______、_________.
6.举出两个主视图和左视图都为矩形的例子:__________、__________.
7.根据下列物体的三视图,填出几何体的名称(或画出图形)
主视图 俯视图 左视图 几何体是_____
主视图 俯视图 左视图 几何体是_____
8.在桌上摆有一些大小相同的正方体木块,主视图.左视图如图,要摆出这样的图形至少需要 块正方体木块,至多需要 块正方体木块.
【拓展延伸】
9.如图是一个有若干个小正方体搭成的几何体的俯视图,其中小正方形格内的数字是小正方体的层数,请你画出它的主视图和左视图.
10.在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要核实一下箱子的数量,于是就想出一个办法:将这堆货物的三视图画了出来,你能根据图中的三视图,帮他清点一下箱子的数量吗?
【探究创新】
11.已知下图为一几何体的三视图:(1)写出这个几何体的名称;(2)任意画出它的一种表面展开图;(3)若主视图的长为10,俯视图中三角形的边长为4,求这个几何体的侧面积.
第五章 走进图形世界
第4节 数学活动——制作礼品盒
第1课时
【基础演练】
1.如图是一个长方体的展开图,如果将它折叠起来,其中点G与点 重合,点L与点 和点 重合.
2.如图,有一个6×6正方形格纸,在四个角各剪去一个1×1的正方形,然后折叠成一个无盖长方体纸盒,求其容积.
3.如果上题中,在四个角各剪去一个2×2的正方形,折叠成一个无盖长方体纸盒,求其容积.
4.问题:用一张边长6cm的正方形纸片制作一个无盖的长方体纸盒,应该怎样制作?怎样制作使得容积较大呢?试给出三种制作方法,并比较制成的纸盒的容积的大小?
【拓展延伸】
1.右图是一多面体的展开图,每个面内都标注了字母,请根据要求回答下列问题:
⑴如果面A在多面体的底部,那么面_______会在上面.
⑵如果面F在前面,从左面看是面B,那么面_______
会在上面.
⑶如果从右面看是面C,面D在后面,那么面_______
会在上面.
2.如果一个长方体的三视图的面积分别为6cm2.3cm2.2cm2,那么这个长方体的体积为__________cm3.
3.骰子是一个正方体,它的相对两个面上的点数之和相等.请在右图中的4×3方格内选择6个相连的正方形,使它们作为一个整体能折成一个骰子的侧面.
(请在图中画出选中部分的轮廓)
4.一种香皂,每一块的长.宽.高分别为16cm.6cm.3cm,现需给这种香皂设计一种包装盒,要求如下:
①每盒装香皂30块;
②香皂相同的面相互对接(外侧的面除外);
③装入香皂后盒内不留空隙;
④包装盒是一个长方体.
⑴根据要求,你一定能设计多种规格的包装盒。请动手试一试,动笔算一算,你认为哪种设计方案最省料?
⑵画出按最省料方案制作的一个包装盒的三视图,计算每一个这样的包装盒需用包装纸多少cm2?(接头粘合部分忽略不计)
第五章 走进图形世界
单元复习小结
一.精心选一选:
1.下面图形是棱柱的是 ( )
A B C D
2.下列图形中,是正方体的平面展开图的是 ( )
A B C D
3.已知某多面体的平面展开图如图所示,其中是三棱柱的有 ( )
A.1个 B.2个 C.3个 D.4个
4.圆锥的侧面展开图是 ( )
A.长方形 B.正方形 C.圆 D.扇形
5.下列交通标志图中,属于轴对称图形的是 ( )
6.如图的陀螺是由下面哪两个几何体组合而成的 ( )
A.长方体和圆锥 B.长方体和三角形
C.圆和三角形 D.圆柱和圆锥
7.如果有一个正方体,它的展开图可能是下面四个展开图中的 ( )
二.细心填一填:
8.长方体有 个面, 条棱, 个顶点.
9.半圆面绕直径旋转一周形成 .
10.一个几何体的三视图是两个同样大小的长方形和一个直径等于长方形一边长的圆,这个几何体是 .
三.努力用一用:
11.如图,是由几个小立方块搭成的几何体的俯视图,小正方形的数字表示该位置小立方块的个数,请画出相应的几何体的主视图及左视图.
12.一个正方体所有相对的面上两数之和相等.下图是它的展开图,请填好图中空白正方形中的数.
13.画出下列几何体的三视图.
第五章达标测试卷
一.精心选一选(每题3分,共计30分)
1.下列立体图形,属于多面体的是 ( )
A.圆柱 B.长方体 C.球 D.圆锥
2.圆柱可以看作由下列哪个图形沿它的一边快速旋转得到 ( )
A.直角三角形 B.梯形 C.长方形 D.等腰三角形
3.两个完全相同的正方体,将一面完全重合,构成的几何体面数有 ( )
A.12个 B.11个 C.10个 D.6个
4.将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到 ( )
A B C D
5.一个立体图形的三视图形如图所示,则该立体图形是 ( )
主视图 左视图 俯视图
A.圆锥 B.球 C.圆柱 D.圆
6.下面图形不能围成一个长方体的是 ( )
7.4张扑克牌如图⑴所示放在桌上,小敏把其中一张旋转180°后得到如图⑵所示,那么她所旋转的牌从左数起是 ( )
A.第一张 B.第二张 C.第三张 D.第四张
8.左图是正方体的表面展开图,如果将其合成原来的正方体(如图)时,与点P重合的两点应该是 ( )
A.S和Z B.T和Y C.U和Y D.T和V
9.将一个正方体沿着某些棱剪开,展成一个平面图形,至少需要剪的棱的条数是 ( )
A.5条 B.6条 C.7条 D.8条
10.有一块正方体木块,它的六个面上分别标上数字1~6,下图是这个正方体木块从不同面所看到的数字情况,请问5对面的数字是 ( )
A.3 B.4 C.6 D.无法确定
二.细心填一填(每题3分,共计24分)
11.如图中的图形2可以看作图形1向下平移 格,再向左平移 格得到.
12.如果某几何体它的俯视图.主视图及左视图都相同,则该几何体可能是 .
13.圆锥的侧面展开图是 形.
14.圆柱由 个面围成,其中 个平面, 个曲面.
15.如图,沿正三角形三边中点连线折起,可拼得一个 .
(第11题图) (第15题图)
16.桌面上放着一个三棱锥和一个圆柱体(如左图),在右图中填上它的视图的名称:
视图 视图 视图
17举出俯视图是圆的三个不同物体的例子:_____._____.______.
18一辆汽车从小明的面前经过,小明拍摄了一组照片.若按照汽车被摄入镜头的先后顺序给下面的照片编号为 .
三.努力用一用(共计46分)
19(4分).如图中按左侧三个图形阴影部分的特点,将右侧的图形补充完整.
20(8分).如图,这是一个由小立方块塔成的几何体的俯视图,小正方形中的数字表示该位置的小立方块的个数.请你画出它的主视图与左视图.
21(6分).如下是七种图形:圆 、线段、 正方形 、长方形、 三角形 、五边形 、六边形
请你选用这七种图形中的若干种(不少于两种)构造一幅图案,并用一句话说明你构想的是什么,例如右图就是符合要求的一个图案.请你在下边构造出两个与之不同的图案,并加以说明.
一辆汽车
22(6分).已知:图(1).图(2)分别是6×6正方形网格上两个轴对称图形(阴影部分),其面积分别为SA.SB(网格中最小的正方形面积为一个平方单位),请观察图形并解答下列问题.
(1)填空:SA∶SB的值是 ;
(2)请你在图(3)的网格上画出一个面积为8个平方单位的图形,要求图形可以看作由其中的一个基本图形经过平移.翻折或旋转形成的.
23(6分).在规格为6×6的正方形网格中,有一个L形图案(如图所示的阴影部分).请你用三种不同的方法分别在下图中再将一个空白的小正方形涂成阴影,使整个阴影部分成为轴对称图形.
24(6分).如图所示,在正方体能见到的面上写上数1.2.3,而在展开图中也已分别写上了两个和一个指定的数.请你在展开图的其它各面上写上适当的数,使得相对的面上两数的和等于7.
25(10分).用一个小立方块搭一个几何体,它的主视图和俯视图如图所示,尝试画出所有可能的左视图.想一想,搭成这个几何体最少需要多少个小立方块?最多需要多少个小立方块?
A B C
图(2)
图(1)
A B C D
图(1)
1
5
2
5
3
4
1
3
?
图(2)
走
A B C D
A B C D
图(1) 图(2)
铁锹
(3)
图(2)
图(1)
图(3)
图(4)
A B C D
图(1)
图(2)
主视图
左视图
俯视图
A
B
C
D
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
图(1)
A B C D
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
