山东省文登市2014届高三第三次统考数学(理)试题
文档属性
| 名称 | 山东省文登市2014届高三第三次统考数学(理)试题 |

|
|
| 格式 | zip | ||
| 文件大小 | 453.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-21 00:00:00 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
( http: / / www.21cnjy.com )
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择 ( http: / / www.21cnjy.com )题)两部分. 共 4页.满分150分,考试时间120分钟. 考试结束,将本试卷答题纸和答题卡一并交回.21世纪教育网版权所有
第Ⅰ卷 选择题(共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上.
2.选择题每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.21cnjy.com
3.答第Ⅱ卷前将答题卡密封线内的项目填写清楚.
4.第Ⅱ卷试题解答要作在答题卡各题规定的矩形区域内,超出该区域的答案无效.
一、 选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.2·1·c·n·j·y
1.设全集 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,集合 HYPERLINK "http://www.21cnjy.com" 则=
A. B. C. D.
2.袋中有个小球,其中红色球个、蓝色球个,白色球个,黄色球个,从中随机抽取个球作成一个样本,则这个样本恰好是按分层抽样方法得到的概率为
A. B. C. D.
3.—空间几何体的三视图如图所示,则此空间几何体的直观图为
( http: / / www.21cnjy.com )
4.已知随机变量服从正态分布.则“”是“ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
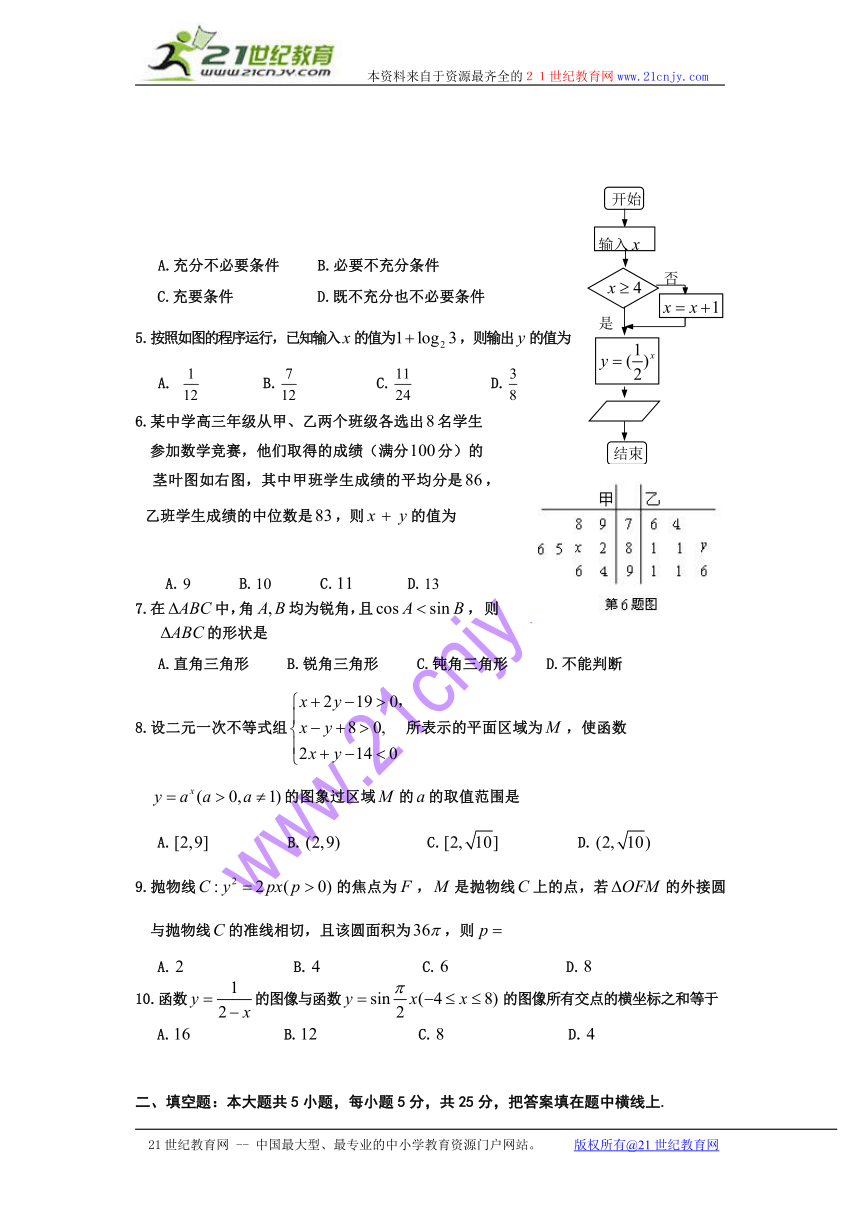
5.按照如图的程序运行,已知输入的值为,则输出的值为
A. B. C. D.
6.某中学高三年级从甲、乙两个班级各选出名学生[来源:21世纪教育网]
参加数学竞赛,他们取得的成绩(满分分)的
茎叶图如右图,其中甲班学生成绩的平均分是, 乙班学生成绩的中位数是,则 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的值为 21教育网
A. B. C. D.
7.在中,角均为锐角,且, 则
的形状是
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能判断
8.设二元一次不等式组所表示的平面区域为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使函数
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象过区域 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围是
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
9.抛物线的焦点为,是抛物线上的点,若的外接圆与抛物线的准线相切,且该圆面积为,则
A. B. C. D.
10.函数的图像与函数的图像所有交点的横坐标之和等于
A. B. C. D.
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上.
11.已知复数满足,则的虚部= .
12.设函数, 则使恒成立的的取值范围为 .
13.已知展开式中,奇数项的二项式系数之和为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则展开式中含项的系数= . www.21-cn-jy.com
14.如图矩形 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 内放置 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 个大小相同的正方形,其中 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 都
在矩形的边上,若向量 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
15.已知是定义在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的不恒为零的函数,且对于任意的满足,,
考查下列结论:①;②为偶函数;③数列为等比数列;④数列为等差数列.其中正确的是_________ . 【来源:21·世纪·教育·网】
三、解答题:本大题共6小题,共75分. 解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
将函数 HYPERLINK "http://www.21cnjy.com" 的图象向右平移后得到图象,已知的部分图象如右图所示,该图象与轴相交于点,与轴相交于点、,点为最高点,且.21·世纪*教育网
(Ⅰ)求函数的解析式,并判断是否是的一个对称中心;
(Ⅱ)在中,、、分别是角、、
的对边,,且,求的最大值.
17.(本小题满分12分)
已知正项数列的前 ( http: / / www.21cnjy.com )项和为且满足.[来源:21世纪教育网]
(Ⅰ)求数列的通项公式;
(Ⅱ)当,( ( http: / / www.21cnjy.com )均为正整数)时,求和的所有可能的乘积之和.
18.(本题满分12分)
如图,直角梯形与等腰直角三角形
所在的平面互相垂直.
.
(Ⅰ)求直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与平面 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 所成角的正切值;
(Ⅱ)线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上是否存在点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 平面 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ?存在请确定具体位置,不存在说明理由.
19.(本题满分12分)
现有正整数,一质点从第一个数出发顺次跳动,质点的跳动步数通过抛掷骰子来决定:骰子的点数小于等于时,质点向前跳一步;骰子的点数大于时,质点向前跳两步.21·cn·jy·com
(Ⅰ)若抛掷骰子二次,质点到达的正整数记为ξ,求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和;
(Ⅱ)求质点恰好到达正整数的概率.
20.(本小题满分13分)
已知圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的右顶点为圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的圆心,左焦点与双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的左顶点重合.
(Ⅰ)求椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程;
(Ⅱ)已知直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 分别交于两点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,与圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 分别交于两点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (其中点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上)且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
( http: / / www.21cnjy.com )
21.(本题满分14分)
设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的一个极值点.
(Ⅰ)求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的关系式(用 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 表示 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ),并求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的单调区间;
(Ⅱ)设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若存在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 成立,求实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围.[来源:21世纪教育网]
201404理科数学 参考答案及评分标准
( http: / / www.21cnjy.com )17解:(Ⅰ)∵, 1分
两式相减得, 2分
由得,又. 3分
∴ 数列 ( http: / / www.21cnjy.com )是首项为,公比为 ( http: / / www.21cnjy.com )的等比数列,
∴ . 5分
(Ⅱ)由 ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )的所有可能乘积(,) 6分
可构成下表
8分
设上表第一行的和为,则 10分
于是…+= 12分
( http: / / www.21cnjy.com )的一个法向量,则必需使 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" .
则,设
,得
令,则.要使 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" ,则有.
此时
所以,线段上存在点,且是靠近点的一个三等分点.(说明:第二问用几何法更简单)
19.(本小题满分12分)
解:(Ⅰ)ξ的可能取值为 …………………1分
………………4分
ξ的分布列为
………………7分
(Ⅱ)质点恰好到达有三种情形
①抛掷骰子五次,出现点数全部小于等于,概率;…………8分
②抛掷骰子四次,出现点数三次小于等于,一次大于,概率为;…………9分
③抛掷骰子三次,出现点数一次小于等于,二次大于,概率 ………………10分
所以
即质点恰好到达正整数的概率为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . ………………12分
20解:(Ⅰ)由题意,圆心 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,双曲线的左顶点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 1分
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,椭圆方程为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 3分
(Ⅱ)设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与椭圆相较于两点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 21世纪教育网
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 5分
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 7分21世纪教育网
点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 到直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的距离 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 9分
显然,若点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 也在线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上,则由于对称性知,直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 就是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 轴,矛盾.
因为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 10分
即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 整理得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 12分
解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 13分
21. (本题满分14分)
解:(Ⅰ)∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 2分
由题意得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 3分
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的一个极值点
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
故 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的关系式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 5分
(1)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得单增区间为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得单减区间为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
(2)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得单增区间为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得单减区间为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ; 8分
(Ⅱ)由(Ⅰ)知:当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上单调递增,在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上单调递减, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )
x≥4
否
是
结束
输入
开始
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
( http: / / www.21cnjy.com )
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择 ( http: / / www.21cnjy.com )题)两部分. 共 4页.满分150分,考试时间120分钟. 考试结束,将本试卷答题纸和答题卡一并交回.21世纪教育网版权所有
第Ⅰ卷 选择题(共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、考号、考试科目用铅笔涂写在答题卡上.
2.选择题每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案,不能答在试题卷上.21cnjy.com
3.答第Ⅱ卷前将答题卡密封线内的项目填写清楚.
4.第Ⅱ卷试题解答要作在答题卡各题规定的矩形区域内,超出该区域的答案无效.
一、 选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.2·1·c·n·j·y
1.设全集 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,集合 HYPERLINK "http://www.21cnjy.com" 则=
A. B. C. D.
2.袋中有个小球,其中红色球个、蓝色球个,白色球个,黄色球个,从中随机抽取个球作成一个样本,则这个样本恰好是按分层抽样方法得到的概率为
A. B. C. D.
3.—空间几何体的三视图如图所示,则此空间几何体的直观图为
( http: / / www.21cnjy.com )
4.已知随机变量服从正态分布.则“”是“ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
5.按照如图的程序运行,已知输入的值为,则输出的值为
A. B. C. D.
6.某中学高三年级从甲、乙两个班级各选出名学生[来源:21世纪教育网]
参加数学竞赛,他们取得的成绩(满分分)的
茎叶图如右图,其中甲班学生成绩的平均分是, 乙班学生成绩的中位数是,则 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" 的值为 21教育网
A. B. C. D.
7.在中,角均为锐角,且, 则
的形状是
A.直角三角形 B.锐角三角形 C.钝角三角形 D.不能判断
8.设二元一次不等式组所表示的平面区域为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使函数
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的图象过区域 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围是
A. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 B. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 C. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 D. HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
9.抛物线的焦点为,是抛物线上的点,若的外接圆与抛物线的准线相切,且该圆面积为,则
A. B. C. D.
10.函数的图像与函数的图像所有交点的横坐标之和等于
A. B. C. D.
二、填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上.
11.已知复数满足,则的虚部= .
12.设函数, 则使恒成立的的取值范围为 .
13.已知展开式中,奇数项的二项式系数之和为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则展开式中含项的系数= . www.21-cn-jy.com
14.如图矩形 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 内放置 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 个大小相同的正方形,其中 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 都
在矩形的边上,若向量 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
15.已知是定义在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上的不恒为零的函数,且对于任意的满足,,
考查下列结论:①;②为偶函数;③数列为等比数列;④数列为等差数列.其中正确的是_________ . 【来源:21·世纪·教育·网】
三、解答题:本大题共6小题,共75分. 解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
将函数 HYPERLINK "http://www.21cnjy.com" 的图象向右平移后得到图象,已知的部分图象如右图所示,该图象与轴相交于点,与轴相交于点、,点为最高点,且.21·世纪*教育网
(Ⅰ)求函数的解析式,并判断是否是的一个对称中心;
(Ⅱ)在中,、、分别是角、、
的对边,,且,求的最大值.
17.(本小题满分12分)
已知正项数列的前 ( http: / / www.21cnjy.com )项和为且满足.[来源:21世纪教育网]
(Ⅰ)求数列的通项公式;
(Ⅱ)当,( ( http: / / www.21cnjy.com )均为正整数)时,求和的所有可能的乘积之和.
18.(本题满分12分)
如图,直角梯形与等腰直角三角形
所在的平面互相垂直.
.
(Ⅰ)求直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与平面 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 所成角的正切值;
(Ⅱ)线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上是否存在点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 平面 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ?存在请确定具体位置,不存在说明理由.
19.(本题满分12分)
现有正整数,一质点从第一个数出发顺次跳动,质点的跳动步数通过抛掷骰子来决定:骰子的点数小于等于时,质点向前跳一步;骰子的点数大于时,质点向前跳两步.21·cn·jy·com
(Ⅰ)若抛掷骰子二次,质点到达的正整数记为ξ,求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 和;
(Ⅱ)求质点恰好到达正整数的概率.
20.(本小题满分13分)
已知圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的右顶点为圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的圆心,左焦点与双曲线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的左顶点重合.
(Ⅰ)求椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的方程;
(Ⅱ)已知直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与椭圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 分别交于两点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,与圆 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 分别交于两点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (其中点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上)且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的值.
( http: / / www.21cnjy.com )
21.(本题满分14分)
设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的一个极值点.
(Ⅰ)求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的关系式(用 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 表示 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ),并求 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的单调区间;
(Ⅱ)设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,若存在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,使得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 成立,求实数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的取值范围.[来源:21世纪教育网]
201404理科数学 参考答案及评分标准
( http: / / www.21cnjy.com )17解:(Ⅰ)∵, 1分
两式相减得, 2分
由得,又. 3分
∴ 数列 ( http: / / www.21cnjy.com )是首项为,公比为 ( http: / / www.21cnjy.com )的等比数列,
∴ . 5分
(Ⅱ)由 ( http: / / www.21cnjy.com )和 ( http: / / www.21cnjy.com )的所有可能乘积(,) 6分
可构成下表
8分
设上表第一行的和为,则 10分
于是…+= 12分
( http: / / www.21cnjy.com )的一个法向量,则必需使 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" .
则,设
,得
令,则.要使 HYPERLINK "http://www.21cnjy.com" HYPERLINK "http://www.21cnjy.com" ,则有.
此时
所以,线段上存在点,且是靠近点的一个三等分点.(说明:第二问用几何法更简单)
19.(本小题满分12分)
解:(Ⅰ)ξ的可能取值为 …………………1分
………………4分
ξ的分布列为
………………7分
(Ⅱ)质点恰好到达有三种情形
①抛掷骰子五次,出现点数全部小于等于,概率;…………8分
②抛掷骰子四次,出现点数三次小于等于,一次大于,概率为;…………9分
③抛掷骰子三次,出现点数一次小于等于,二次大于,概率 ………………10分
所以
即质点恰好到达正整数的概率为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 . ………………12分
20解:(Ⅰ)由题意,圆心 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,双曲线的左顶点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 1分
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,椭圆方程为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 3分
(Ⅱ)设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与椭圆相较于两点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 21世纪教育网
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 5分
所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 7分21世纪教育网
点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 到直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的距离 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
则 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 9分
显然,若点 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 也在线段 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上,则由于对称性知,直线 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 就是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 轴,矛盾.
因为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,所以 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , 10分
即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 整理得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 12分
解得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 13分
21. (本题满分14分)
解:(Ⅰ)∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 2分
由题意得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 3分
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 且 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
令 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
∵ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 是函数 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的一个极值点
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
故 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 与 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 的关系式 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 5分
(1)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得单增区间为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得单减区间为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
(2)当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得单增区间为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
由 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 得单减区间为: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 、 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ; 8分
(Ⅱ)由(Ⅰ)知:当 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上单调递增,在 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 上单调递减, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 , HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4
( http: / / www.21cnjy.com )
x≥4
否
是
结束
输入
开始
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
