8.6.1 直线与直线垂直 同步练习(含解析)
文档属性
| 名称 | 8.6.1 直线与直线垂直 同步练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 215.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 11:46:04 | ||
图片预览


文档简介
《第六节 空间直线、平面的垂直》同步练习
(课时1 直线与直线垂直)
一、基础巩固
知识点1 异面直线所成的角
1.[2022河南开封五县高一下期中]在正方体ABCD-A1B1C1D1的所有面对角线中,所在直线与直线A1B互为异面直线且所成角为60°的面对角线的条数为( )
A.2 B.4 C.6 D.8
2.正四面体P-ABC中,点M是BC的中点,则异面直线PM与AB所成角的余弦值为( )
A. B. C. D.
3.[2022河北沧州二模]《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.如图,若AB,CD都是直角圆锥SO底面圆的直径,且∠AOD=,则异面直线SA与BD所成角的余弦值为( )
A. B. C. D.
4.如图,在三棱锥A-BCD中,AB=CD,且直线AB与CD所成的角为60°,点M,N分别是BC,AD的中点,则异面直线AB与MN所成角的大小为 .
知识点2 直线与直线垂直
5.在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面ABCD是菱形,且AB=2,∠ABC=120°,若A1B⊥AD1,试求AA1的长度.
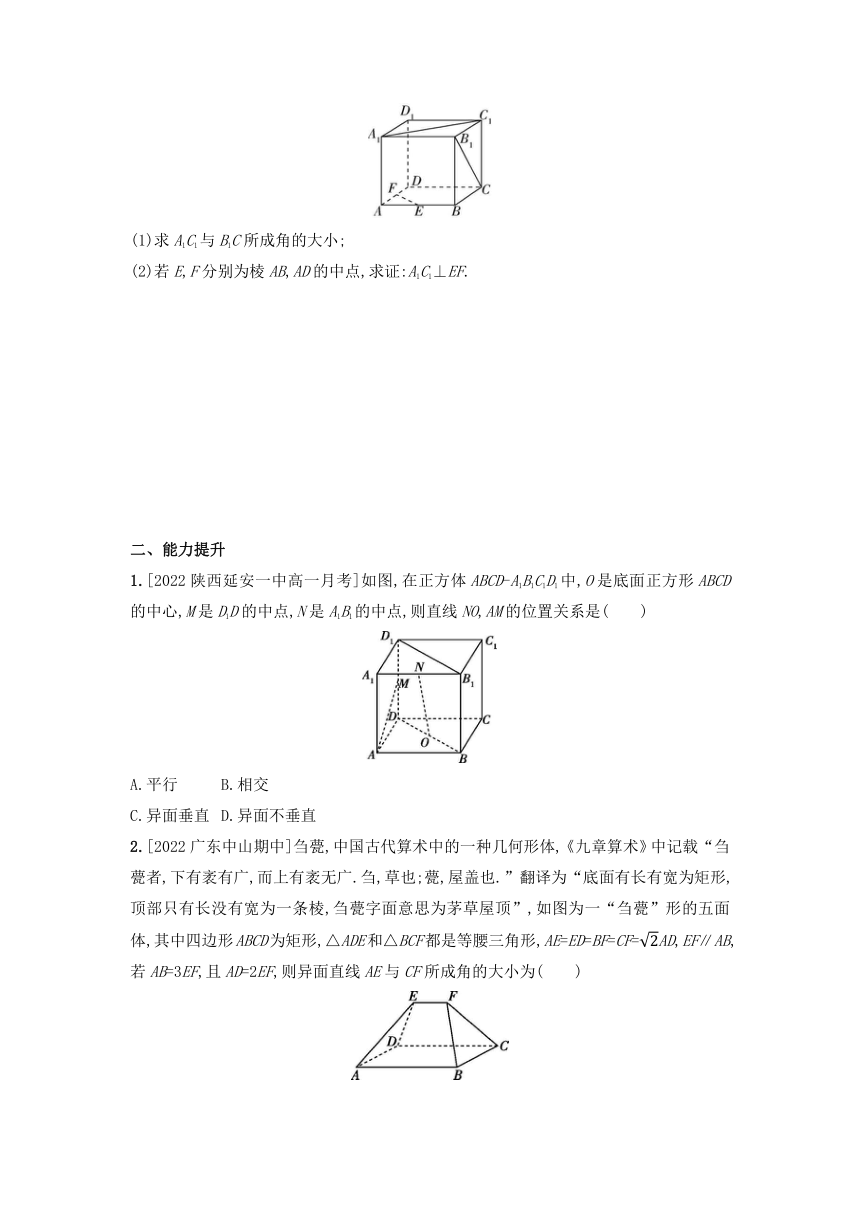
6.如图,已知正方体ABCD-A1B1C1D1.
(1)求A1C1与B1C所成角的大小;
(2)若E,F分别为棱AB,AD的中点,求证:A1C1⊥EF.
二、能力提升
1.[2022陕西延安一中高一月考]如图,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则直线NO,AM的位置关系是( )
A.平行 B.相交
C.异面垂直 D.异面不垂直
2.[2022广东中山期中]刍甍,中国古代算术中的一种几何形体,《九章算术》中记载“刍甍者,下有袤有广,而上有袤无广.刍,草也;甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱,刍甍字面意思为茅草屋顶”,如图为一“刍甍”形的五面体,其中四边形ABCD为矩形,△ADE和△BCF都是等腰三角形,AE=ED=BF=CF=AD,EF∥AB,若AB=3EF,且AD=2EF,则异面直线AE与CF所成角的大小为( )
A. B. C. D.
3.[2022河北邯郸高一期中]已知直三棱柱ABC-A1B1C1中,AC⊥BC,AB=2AC=2AA1=4,则异面直线AC1与B1C所成角的余弦值为( )
A. B. C. D.
4.[2022湖北省黄石市大冶市第一中学高二上月考]在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.若AC=BD=a,且AC与BD所成的角为60°,则EG的长为( )
A.a B. C.a或a D.或a
5.如图,已知点P在圆柱OO1的底面☉O上,AA1⊥AB,BP⊥A1P,AB,A1B1分别为☉O,☉O1的直径,且AB∥A1B1.若圆柱OO1的体积V=12π,OA=2,∠AOP=120°,回答下列问题.
(1)求三棱锥A1-APB的体积.
(2)在线段AP上是否存在一点M,使异面直线OM与A1B所成的角的余弦值为 若存在,请指出点M的位置,并证明;若不存在,请说明理由.
参考答案
一、基础巩固
1.B 如图,易知△A1BC1为等边三角形,所以∠BA1C1=60°,又AC∥A1C1,所以异面直线AC与A1B的夹角为60°,符合题设.同理,面对角线B1C,B1D1,AD1也满足题意,所以满足条件的面对角线共4条,故选B.
2.B 如图,取AC的中点N,连接PN,MN.设正四面体P-ABC的棱长为2,则PM=PN=,MN=1,且MN∥AB,所以∠PMN是异面直线PM与AB所成角,故异面直线PM与AB所成角的余弦值为cos∠PMN=.故选B.
3.C 如图,连接AD,BC,AC,SC.因为O为AB,CD的中点,且AB=CD,所以四边形ADBC为矩形,所以DB∥AC,所以∠SAC或其补角为异面直线SA与BD所成的角.设圆O的半径为1,则SA=SC=.因为∠AOD=,所以∠ADO=.在直角△DAC中,CD=2,得AC=.所以cos∠SAC=,所以异面直线SA与BD所成角的余弦值为.故选C.
4.60°或30° 解析如图,取AC的中点P,连接PM,PN,则PM∥AB,且PM=AB,PN∥CD,且PN=CD,所以∠MPN为异面直线AB与CD所成的角或所成角的补角,则∠MPN=60°或∠MPN=120°.若∠MPN=60°,因为PM∥AB,所以∠PMN是异面直线AB与MN所成的角或所成角的补角.又AB=CD,所以PM=PN,则△PMN是等边三角形,所以∠PMN=60°,即异面直线AB与MN所成的角为60°.若∠MPN=120°,则易知△PMN是等腰三角形,所以∠PMN=30°,即异面直线AB与MN所成的角为30°.综上,异面直线AB与MN所成的角为60°或30°.
5.解析连接CD1,AC,由题意,得A1D1∥BC,A1D1=BC,
所以四边形A1BCD1是平行四边形,所以A1B∥CD1,
所以∠AD1C(或其补角)为A1B和AD1所成的角.
因为异面直线A1B和AD1所成的角为90°,所以∠AD1C=90°,
易得AD1=CD1,所以△AD1C是等腰直角三角形.
所以AD1=AC.
又底面ABCD是菱形,且AB=BC=2,∠ABC=120°,所以AC=2×sin 60°×2=6,所以AD1=AC=3,
所以AA1=.
6.解析(1)如图,连接AC,AB1.
由几何体ABCD-A1B1C1D1是正方体,知四边形AA1C1C为平行四边形,所以AC∥A1C1,
从而AC与B1C所成的角为A1C1与B1C所成的角.
由AB1=AC=B1C,可知∠B1CA=60°.
故A1C1与B1C所成的角为60°.
(2)如图,连接BD.
易知四边形AA1C1C为平行四边形,所以AC∥A1C1.
因为EF为△ABD的中位线,所以EF∥BD.
又AC⊥BD,所以EF⊥AC,所以A1C1⊥EF.
二、能力提升
1.C 如图,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,连接A1O,B1O,设E,F分别是AD,BC的中点,连接EF,A1E,ON,则E,O,F三点共线,且EF与AB和A1B1平行且相等,也即EO与A1N平行且相等,则四边形A1NOE是平行四边形,所以NO∥A1E.在正方形ADD1A1中,△A1AE≌△ADM,所以∠AA1E=∠DAM,所以∠DAM +
∠AEA1=∠AA1E+∠AEA1=90°,所以AM⊥A1E,所以直线NO⊥AM,因为它们不相交,故选C.
2.C 如图,设EF=1,在AB上取点G满足AG=EF=1,故AG∥EF且AG=EF,故四边形AGFE是平行四边形,故AE∥GF,异面直线AE与CF所成角为∠GFC(或其补角),GF=AE=CF=2,CG==2,故△GFC为等边三角形,故∠GFC=.故选C.
3.C 如图所示,把三棱柱补成四棱柱,由题意得BC=2,易知该四棱柱为长方体,CD=AB=4,异面直线AC1与B1C所成角为∠C1AD1(或其补角),C1D1=CD=4,AC1==2,AD1==4,所以cos∠C1AD1=.故选C.
4.D 如图所示,因为E,F,G,H分别是AB,BC,CD,DA的中点,所以EF∥AC∥HG,EF=HG=AC=a,EH∥BD∥FG,EH=FG=BD=a,所以四边形EFGH为菱形.又AC与BD所成的角为60°,所以EF与FG所成角为60°,所以菱形的边长为a,相邻两个内角分别为 60°,120°,即∠EFG=120°或∠EFG=60°,所以EG=2FGsin 60°=a或EG=2FGsin 30°=a.故选D.
5.解析(1)由题意,得V=π·OA2·AA1=4π·AA1=12π,解得AA1=3.
由OA=2,∠AOP=120°,得∠BAP=30°,BP=2,AP=2,
所以S△PAB=×2×2=2,
所以三棱锥A1-APB的体积S△PAB·AA1=×2×3=2.
(2)当点M为AP的中点时,异面直线OM与A1B所成的角的余弦值为.
证明如下:
因为O,M分别为AB,AP的中点,所以OM∥BP,
所以∠A1BP就是异面直线OM与A1B所成的角.
因为AA1=3,AB=4,AA1⊥AB,所以A1B=5.
又BP⊥A1P,所以cos∠A1BP=,
所以当点M为AP的中点时,异面直线OM与A1B所成的角的余弦值为 .
(课时1 直线与直线垂直)
一、基础巩固
知识点1 异面直线所成的角
1.[2022河南开封五县高一下期中]在正方体ABCD-A1B1C1D1的所有面对角线中,所在直线与直线A1B互为异面直线且所成角为60°的面对角线的条数为( )
A.2 B.4 C.6 D.8
2.正四面体P-ABC中,点M是BC的中点,则异面直线PM与AB所成角的余弦值为( )
A. B. C. D.
3.[2022河北沧州二模]《几何原本》是古希腊数学家欧几里得的一部不朽之作,其第十一卷中称轴截面为等腰直角三角形的圆锥为直角圆锥.如图,若AB,CD都是直角圆锥SO底面圆的直径,且∠AOD=,则异面直线SA与BD所成角的余弦值为( )
A. B. C. D.
4.如图,在三棱锥A-BCD中,AB=CD,且直线AB与CD所成的角为60°,点M,N分别是BC,AD的中点,则异面直线AB与MN所成角的大小为 .
知识点2 直线与直线垂直
5.在四棱柱ABCD-A1B1C1D1中,侧面都是矩形,底面ABCD是菱形,且AB=2,∠ABC=120°,若A1B⊥AD1,试求AA1的长度.
6.如图,已知正方体ABCD-A1B1C1D1.
(1)求A1C1与B1C所成角的大小;
(2)若E,F分别为棱AB,AD的中点,求证:A1C1⊥EF.
二、能力提升
1.[2022陕西延安一中高一月考]如图,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,则直线NO,AM的位置关系是( )
A.平行 B.相交
C.异面垂直 D.异面不垂直
2.[2022广东中山期中]刍甍,中国古代算术中的一种几何形体,《九章算术》中记载“刍甍者,下有袤有广,而上有袤无广.刍,草也;甍,屋盖也.”翻译为“底面有长有宽为矩形,顶部只有长没有宽为一条棱,刍甍字面意思为茅草屋顶”,如图为一“刍甍”形的五面体,其中四边形ABCD为矩形,△ADE和△BCF都是等腰三角形,AE=ED=BF=CF=AD,EF∥AB,若AB=3EF,且AD=2EF,则异面直线AE与CF所成角的大小为( )
A. B. C. D.
3.[2022河北邯郸高一期中]已知直三棱柱ABC-A1B1C1中,AC⊥BC,AB=2AC=2AA1=4,则异面直线AC1与B1C所成角的余弦值为( )
A. B. C. D.
4.[2022湖北省黄石市大冶市第一中学高二上月考]在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点.若AC=BD=a,且AC与BD所成的角为60°,则EG的长为( )
A.a B. C.a或a D.或a
5.如图,已知点P在圆柱OO1的底面☉O上,AA1⊥AB,BP⊥A1P,AB,A1B1分别为☉O,☉O1的直径,且AB∥A1B1.若圆柱OO1的体积V=12π,OA=2,∠AOP=120°,回答下列问题.
(1)求三棱锥A1-APB的体积.
(2)在线段AP上是否存在一点M,使异面直线OM与A1B所成的角的余弦值为 若存在,请指出点M的位置,并证明;若不存在,请说明理由.
参考答案
一、基础巩固
1.B 如图,易知△A1BC1为等边三角形,所以∠BA1C1=60°,又AC∥A1C1,所以异面直线AC与A1B的夹角为60°,符合题设.同理,面对角线B1C,B1D1,AD1也满足题意,所以满足条件的面对角线共4条,故选B.
2.B 如图,取AC的中点N,连接PN,MN.设正四面体P-ABC的棱长为2,则PM=PN=,MN=1,且MN∥AB,所以∠PMN是异面直线PM与AB所成角,故异面直线PM与AB所成角的余弦值为cos∠PMN=.故选B.
3.C 如图,连接AD,BC,AC,SC.因为O为AB,CD的中点,且AB=CD,所以四边形ADBC为矩形,所以DB∥AC,所以∠SAC或其补角为异面直线SA与BD所成的角.设圆O的半径为1,则SA=SC=.因为∠AOD=,所以∠ADO=.在直角△DAC中,CD=2,得AC=.所以cos∠SAC=,所以异面直线SA与BD所成角的余弦值为.故选C.
4.60°或30° 解析如图,取AC的中点P,连接PM,PN,则PM∥AB,且PM=AB,PN∥CD,且PN=CD,所以∠MPN为异面直线AB与CD所成的角或所成角的补角,则∠MPN=60°或∠MPN=120°.若∠MPN=60°,因为PM∥AB,所以∠PMN是异面直线AB与MN所成的角或所成角的补角.又AB=CD,所以PM=PN,则△PMN是等边三角形,所以∠PMN=60°,即异面直线AB与MN所成的角为60°.若∠MPN=120°,则易知△PMN是等腰三角形,所以∠PMN=30°,即异面直线AB与MN所成的角为30°.综上,异面直线AB与MN所成的角为60°或30°.
5.解析连接CD1,AC,由题意,得A1D1∥BC,A1D1=BC,
所以四边形A1BCD1是平行四边形,所以A1B∥CD1,
所以∠AD1C(或其补角)为A1B和AD1所成的角.
因为异面直线A1B和AD1所成的角为90°,所以∠AD1C=90°,
易得AD1=CD1,所以△AD1C是等腰直角三角形.
所以AD1=AC.
又底面ABCD是菱形,且AB=BC=2,∠ABC=120°,所以AC=2×sin 60°×2=6,所以AD1=AC=3,
所以AA1=.
6.解析(1)如图,连接AC,AB1.
由几何体ABCD-A1B1C1D1是正方体,知四边形AA1C1C为平行四边形,所以AC∥A1C1,
从而AC与B1C所成的角为A1C1与B1C所成的角.
由AB1=AC=B1C,可知∠B1CA=60°.
故A1C1与B1C所成的角为60°.
(2)如图,连接BD.
易知四边形AA1C1C为平行四边形,所以AC∥A1C1.
因为EF为△ABD的中位线,所以EF∥BD.
又AC⊥BD,所以EF⊥AC,所以A1C1⊥EF.
二、能力提升
1.C 如图,在正方体ABCD-A1B1C1D1中,O是底面正方形ABCD的中心,M是D1D的中点,N是A1B1的中点,连接A1O,B1O,设E,F分别是AD,BC的中点,连接EF,A1E,ON,则E,O,F三点共线,且EF与AB和A1B1平行且相等,也即EO与A1N平行且相等,则四边形A1NOE是平行四边形,所以NO∥A1E.在正方形ADD1A1中,△A1AE≌△ADM,所以∠AA1E=∠DAM,所以∠DAM +
∠AEA1=∠AA1E+∠AEA1=90°,所以AM⊥A1E,所以直线NO⊥AM,因为它们不相交,故选C.
2.C 如图,设EF=1,在AB上取点G满足AG=EF=1,故AG∥EF且AG=EF,故四边形AGFE是平行四边形,故AE∥GF,异面直线AE与CF所成角为∠GFC(或其补角),GF=AE=CF=2,CG==2,故△GFC为等边三角形,故∠GFC=.故选C.
3.C 如图所示,把三棱柱补成四棱柱,由题意得BC=2,易知该四棱柱为长方体,CD=AB=4,异面直线AC1与B1C所成角为∠C1AD1(或其补角),C1D1=CD=4,AC1==2,AD1==4,所以cos∠C1AD1=.故选C.
4.D 如图所示,因为E,F,G,H分别是AB,BC,CD,DA的中点,所以EF∥AC∥HG,EF=HG=AC=a,EH∥BD∥FG,EH=FG=BD=a,所以四边形EFGH为菱形.又AC与BD所成的角为60°,所以EF与FG所成角为60°,所以菱形的边长为a,相邻两个内角分别为 60°,120°,即∠EFG=120°或∠EFG=60°,所以EG=2FGsin 60°=a或EG=2FGsin 30°=a.故选D.
5.解析(1)由题意,得V=π·OA2·AA1=4π·AA1=12π,解得AA1=3.
由OA=2,∠AOP=120°,得∠BAP=30°,BP=2,AP=2,
所以S△PAB=×2×2=2,
所以三棱锥A1-APB的体积S△PAB·AA1=×2×3=2.
(2)当点M为AP的中点时,异面直线OM与A1B所成的角的余弦值为.
证明如下:
因为O,M分别为AB,AP的中点,所以OM∥BP,
所以∠A1BP就是异面直线OM与A1B所成的角.
因为AA1=3,AB=4,AA1⊥AB,所以A1B=5.
又BP⊥A1P,所以cos∠A1BP=,
所以当点M为AP的中点时,异面直线OM与A1B所成的角的余弦值为 .
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
