苏科版七年级上第3章用字母表示数全章课课练(无答案)[上学期]
文档属性
| 名称 | 苏科版七年级上第3章用字母表示数全章课课练(无答案)[上学期] |  | |
| 格式 | rar | ||
| 文件大小 | 96.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-12-03 19:53:00 | ||
图片预览




文档简介
第三章 用字母表示数
第1节 用字母表示数
【基础演练】
⒈买单价为a元的温度计n个,付出b元,应找回钱数是 ( )
A.(b-a)元 B.(b-n)元 C.(na-b)元 D.(b-na)元
⒉一个两位数,十位上的数字为a,个位上的数字比十位上的数字的一半多5,那么这个两位数是 ( )
A.10a+(+5) B.10a+(-5) C.10a+(2a-5) D.10a+(2a-10)
⒊已知长方形的周长是m厘米,一边长为a厘米,则这个长方形的面积是 ( )
A.平方厘米 B.(—a)平方厘米
C.a(—a)平方厘米 D.平方厘米,
⒋第二十届电视剧飞天奖今年有a部作品参赛,比去年增加了40℅还多2部,设去年参赛的作品有b部,则b是 ( )
A. B. C.a(1+40%)+2 D.a(1+40%)-2
【深入练习】
⒌某工厂一月份生产机床m台,二月份比一月份增产10%,则二月份生产机床 台,
⒍某商品8折优惠售价为x元,则原价是 元.
⒎ 三个连续的偶数,中间一个是n. 则其余两个分别是 、 .
⒏ 汽车的速度是v米/秒,火车的速度比汽车的速度的2倍少15米/秒,则火车的速度
是 米/秒.
⒐ 观察下列各式:
1×3=1+2×1 2×4=2+2×2 ………
3×5=3+2×3 4×6=4+2×4
请你将猜想到的规律用正整数n(n≥1) 表示出来 .
10.将一个边长为1的正方形分成两个相同的矩形,再将其中的一个矩形分成两个相同的矩形……以此类推不断地分下去,不用通分,观察图形你能一下子计算出下式的结果吗
.
【拓展延伸】
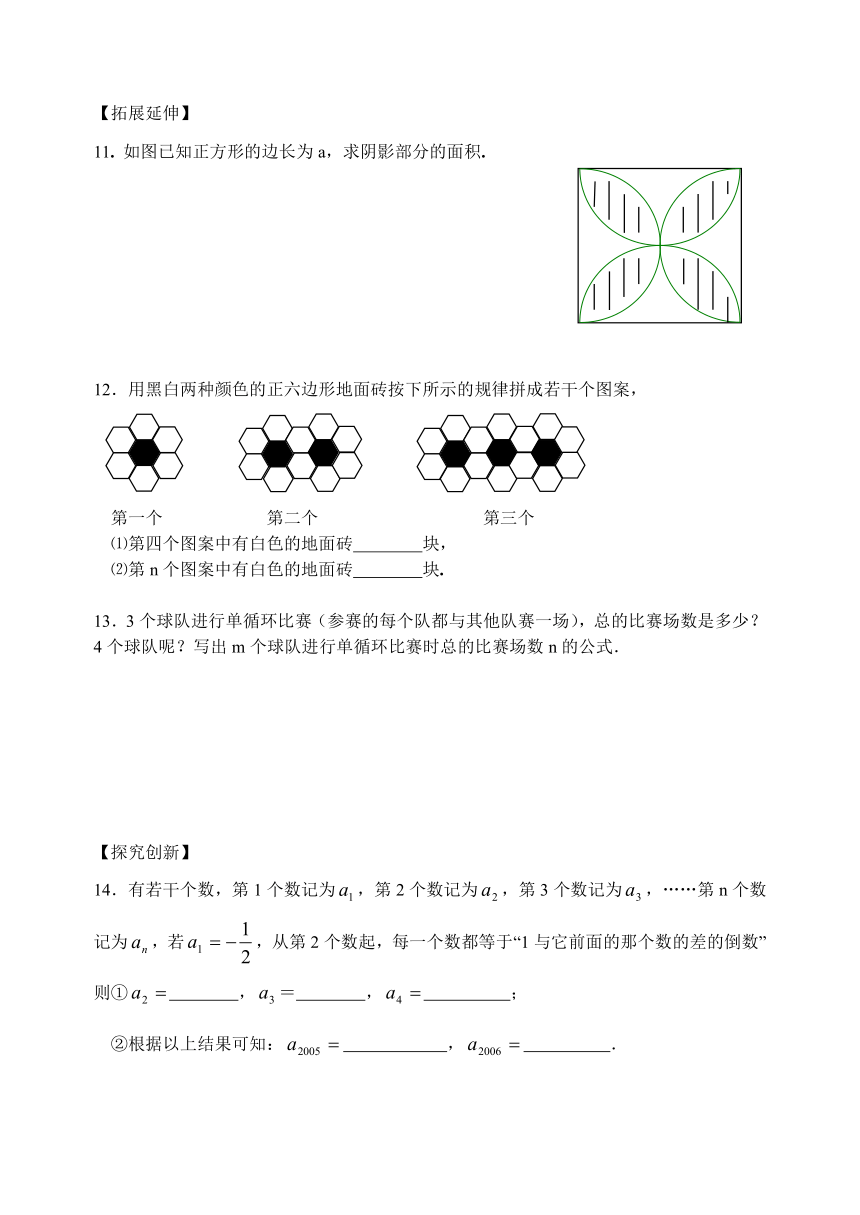
11. 如图已知正方形的边长为a,求阴影部分的面积.
12.用黑白两种颜色的正六边形地面砖按下所示的规律拼成若干个图案,
第一个 第二个 第三个
⑴第四个图案中有白色的地面砖 块,
⑵第n个图案中有白色的地面砖 块.
13.3个球队进行单循环比赛(参赛的每个队都与其他队赛一场),总的比赛场数是多少?4个球队呢?写出m个球队进行单循环比赛时总的比赛场数n的公式.
【探究创新】
14.有若干个数,第1个数记为,第2个数记为,第3个数记为,……第n个数记为,若,从第2个数起,每一个数都等于“1与它前面的那个数的差的倒数”则① ,= , ;
②根据以上结果可知: , .
第三章 用字母表示数
第2节 代数式(第1课时)
【基础演练】
⒈下列式子中符合代数式的书写格式的是 ( )
A.x·20y B.2÷ab C.(a-b)千克 D.2mn千米
⒉下列说法正确的是 ( )
A.0、b、都是整式 B.单项式a没有系数
C.没有加减运算的代数式是单项式
D.x—2xy—y是由x、—2xy、—y三项组成.
⒊设甲数为a,甲数比乙数小20%,用代数式表示乙数 ( )
A.a-20% B.(1-20%)a C.(1+20%)a D.
⒋某校阶梯教室第一排有m个座位,后面每排比前一排多2个座位,则第n排的座位数
是 ( )
A.m+2n B.mn+2 C.m+2(n—1) D.m+(n+2)
⒌一家三口准备外出旅游,甲乙两家的旅行社的报价相同,为了竞争,甲旅行社说:“父亲买全票,其它人可享受6折优惠”.乙旅行社说:“家庭旅行可按团体票计价,按原价的优惠”,由此可以判断 ( )
A.甲比乙优惠 B.乙比甲优惠 C.甲乙收费相同 D.以上都有可能
⒍如图用火柴棒搭正方形,甲、乙、丙、丁四位同学都用x表示所搭正方形的个数,从而计算火柴棒的根数,他们计算的结果分别是:
甲:4+3(X-1); 乙:x+x+(x+1);
丙:1+3x; 丁:4x-(x-1).
其中计算结果正确的同学有 ( )
A.1位 B.2位 C.3位 D.4位
【深入练习】
⒎若n为正整数,用代数式表示:
1 中间一个数为n的三个连续整数为 .
2 与2n相邻的奇数为 .
3 最大的一个是2n+2的三个连续的偶数 .
⒏某车间第一年的产值为a万元,第二年的产值增加x%,第三年的产值又比第二年增加x%,则第三年的产值为 万元,
⒐代数式-是______次单项式,系数为________.
⒑托运行李p千克(p为整数)的费用标准:已知托运第1个1千克需付2元,以后每增加1千克(不足1千克按1千克计)需增加费用5角.若某人托运p千克(p>1)的行李,则托运费用为 .
【拓展延伸】
⒒用代数式表示下列各题:
①比x的3倍大6的数, ②比x小6的数的三分之一,
③a、b两数的和与a、b两数差的积, ④被5除商为n余3的数,
⒓某种商品每件的成本为5元,售价比成本高10%,如果售了a件,那么销售总额为b元,用a的代数式表示b.
⒔一个三位数,它的十位上的数字是百位上数字的3倍,个位上的数字是百位上数字的2倍.设这个三位数个位上的数字是x,十位上的数字为y,百位上的数字为z.
(1)用含x、y、z的代数式表示这个三位数 ;
(2)用含z的代数式表示这个三位数 ;
(3)写出所有满足题目条件的三位数 .
【探究创新】
⒕学校组织学生到距离学校6km的光明科技馆去参观,学生李明因事没能乘上学校的包车,于是准备在校门口乘出租车去光明科技馆,出租车收费标准如下:
里程 收费∕元
3km以下(含3km) 8.00
3km以上(每增加1km) 1.80
⑴若出租车行驶的里程为xkm(x>3)请用x的代数式表示车费y元.
⑵李明身上仅有14元钱,够不够支付乘出租车到科技馆的车费?
请说明理由.
第三章 用字母表示数
第3节 代数式的值(第1课时)
【基础演练】
⒈当x=-1时,代数式|5x+2|和1-3x的值分别为M、N,则M、N之间的关系为 ( )
A.M>N B. M<N C. M=N D. 以上答案都有可能
⒉当a=-2时,代数式-a2的值是 ( )
A.4 B.-2 C.-4 D.2
⒊已知a-b=-2,则代数式3(a-b)2-b+a的值为 ( )
A. 10 B. 12 C. -10 D.-12
⒋小王利用计算机设计了一个计算程序,输入与输出的数据如下表:
输入 1 2 3 4 5 …
输出 …
当输入数据8时,输出的数据是 ( )
A. B. C. D.
【深入练习】
⒌已知:x=-1,y=2, 则(x-y)2-x3+x2y2 = .
⒍已知:a=,b=,则a2-2ab+b2= .
⒎当m-n=5, mn= -2,则代数式(n-m)2-4mn= .
⒏已知:x2+xy=1,xy-y2=-4,则x2+2xy-y2= .
⒐若m2+3n-1的值为5,则代数式2m2+6n+1的值为 .
10. 则代数式的值为 .
【拓展延伸】
11. 若(a+3)2+|b-4|=0分别求下列代数式的值:
(1) (a+b) -(a-b)2 (2) 2a-3b + a2+2b2
12.经批准,某商品的价格可在定价的基础上根据市场行情最多上浮20%,最多下浮30%.
(1) 若这种商品定价为a元,那么这种商品的售价可以在什么范围内?
(2) 若定价为100元,那么售价可在什么范围内?
13.按图示的计算程序计算并填写下表:
输入 0 0.3 3
输出
【探究创新】
14.当a=-0.5,b=0.25时,求下列代数式的值:
(1) (a+b)2 (2) a2+2ab+b2
(3) 回答下问题:
①这两个代数式的值有什么关系?
②当a=2,b=-3时,上述结论是否仍然成立?
③再自选一组a、b的值试一试.
④你能用简便的方法算出当a=-0.875,b=-0.125时,代数式a2+2ab+b2的值吗?
第三章 用字母表示数
第3节 代数式的值(第2课时)
【基础演练】
⒈右图所示是一个数值转换机,输入x,输出3(x-1),下面给出了四种转换步骤,其中不正确的是 ( )
A.先减去1,再乘以3
B.先乘以3,再减去1? 输入x 输出3(x-1)
C.先乘以3,再减去3
D.先加上-1,再乘以3
⒉下列代数式的值一定是正数的是 ( )
A.(a+1)2 B.|x+3| C.1+(-b)2 D.1-(-y)2
⒊已知a、b互为相反数,c、d互为倒数,|m|=2,则代数式110(a+b)2+3cd-的值为 ( )
A.2 B.3 C.4 D.5
⒋若x=3a,y=3x,则x-y+a等于 ( )
A.a B.10a C.-5a D.-a
⒌若时,代数式的值为5,则时,代数式的值等于( )
A .0 B.-3 C.-4 D.-5
【深入练习】
⒍华氏温度f和摄氏温度c的关系是:f=c+32,当人的体温为37度时,华氏温度
为 度.
⒎甲每天可做x个零件,乙每天可做y个零件,两人同时工作共做m个零件,需要的时间为 天,若x=25,y=30,m=385,则两人需 天完成任务.
⒏某百货商厦元月份的销售额为a元,二月份比元月份的销售额多b元,三月份比二月份减少10%,则第一季度的销售额总计为 元.当a=30000,b=5000时,第一季度的总销售额为 元.
⒐某市为鼓励市民节约用水,对自来水用户按如下标准收费:若每月用户用水不超过20m3,则每立方米按x元收费;若超过20 m3,则超过的部分按y元收费;若居民在一个月内用水35 m3,则他该月应缴水费 元.
【拓展延伸】
10.填写下表,并观察下列两个代数式的值的变化.
x 1 2 3 4 5 6 ……
-2x-6
-x2
估计一下,哪个代数式的值会先小于-100?
11.生物学家发现,气温y在一定温度内时,某地种蟋蟀每分钟鸣叫的次数x与气温y(单位:℃)有一定的关系,下表是通过实验得到的一组数据:
x(次/分) 20 30 40 50 60 …
y(℃) 25 25+2.5 25+5 25+7.5 25+10 …
(1)根据表中的数据,写出y与x之间的关系式
(2)当这种蟋蟀每分钟鸣叫56次时,该地当时的气温多少
【探究创新】
12. 你能比较两个数的大小吗?
为了解决这个问题,我们首先把它抽象成一般开工,即比较的大小(n为自然数),我们从分析特殊向简单的情形入手,n=1,n=2,n=3,…的分析,从中发现规律,经过归纳,猜想出结论.
(1)计算,比较下列各组数中两个数大小(在空格中填“>”、“=”、“<”)
2, , , , ,…
(2)从上面的结果进行归纳猜想,的大小关系是 .
(3)根据上面的归纳猜想出一般结论,试比较的大小.
第三章 用字母表示数
第4节 合并同类项(第1课时)
【基础演练】
⒈下列各组式子中,是同类项的是 ( )
A. 3x2y和-3xy2 B. 5ab和-7bac C. 2x2和2x3 D. 23和-15
⒉下列合并同类项正确的是 ( )
A. 5m2n-3m2n =2 B. 2a2+3a4=5a6
C. -x2-x2-x2=-3x2 D. -ab-ab=0
⒊多项式7a2-6a3b+3a2b+3a2+6a3b-3a2b-10a2的值 ( )
A. 与字母a,b都有关 B. 只与字母a有关
C. 只与字母b有关 D. 与字母a,b都无关
【深入练习】
⒋若单项式xm+1y2与-x3yn-1是同类项,则m=________, n=________.
⒌三个连续的奇数中,最小的一个是2n-1,则这三个连续奇数的和为________.
⒍七年级(9)班给“希望工程”捐款x元,七年级(1)班比(9)班多10元,七年级(8)班捐的钱是(9)班的2倍少30元,这3个班共捐款__________元
【拓展延伸】
7.合并同类项:
(1) 5ab2-7a2b-8ab2-3a2b
(2) x2y2-3xy-7x2y2+xy-1+5x2y2
(3)(m+2n)2-5(m-n)-(m+2n)2 +3(m-n)
8. 已知、满足|-1|+(3+2-7)2=0,有下列单项式:(1);
(2);(3) .试判断其中是否有同类项?若有,请指出.
9.求代数式的值:2x2-5xy+2y2-x2-xy-2y2-3x2+5,其中x=-1,y=-.
10.已知t=-,求代数式2(t2-t-1)-(t2-t-1)+3(t2-t-1)的值.
11.某商场1月份销售额a万元,2月份销售额比1月份增长10%,3月份比前两个月的和少a万元,求该商场第一季度总销售额. 若a=100,求第一季度总销售额是多少万元?
【探究创新】
12.若多项式的值与无关,求的值.
第三章 用字母表示数
第4节 合并同类项(第2课时)
【基础演练】
⒈下列各组代数式中,不是同类项的是 ( )
A. B. C. D.
⒉下列合并同类项正确的是 ( )
A. B.
C. D.
⒊已知则多项式的值为 ( )
A.-1 B. C.1 D.
⒋已知多项式ax+bx合并后结果为零,则下列说法正确的是 ( )
A.a=b=0 B.a=b=x=0 C.a+b=0 D.a-b=0
⒌已知是同类项,则代数式的值是 ( )
A.-1 B.0 C.1 D.无法求得
【深入练习】
⒍当m= ,n= 时,和是同类项
⒎三角形的三边长分别为5x,12x,13x,则这个三角形的周长为 ,当x=2cm时,周长为 cm.
⒏合并同类项: .
【拓展延伸】
⒐合并同类项:
(1)
(2)
10.求下列各式的值:
(1) 2x2y-3xy+x2-2x2y+5xy-x2,其中x=4,y=-3.
(2) ,其中
11.已知:x2+y2=7,xy=-2. 求5x2-3xy-4y2-11xy-7x2+2y2的值.
【探究创新】
12.在“计算4a2-2ab+3b-a2+2ab-5-3a2的值,其中a=-,b=3 ”的解题过程中,小芳把a=-错写成a=,小华错写成a=.但他们的答案都是正确的,你知道这是什么原因吗?
第三章 用字母表示数
第5节 去括号(第1课时)
【基础演练】
⒈下列式子中,去括号后得a-b+c的是 ( )
A. a-(b+c) B. -(a-b)+c C. a-(b-c) D. -(a+b)+c
⒉下列去括号中正确的是 ( )
A.a2-(2a-b+c)=a2-2a-b+c B.x2+3(x-1)=x2+3x-1
C.3m-[5b-(2c-1)]=3a-5b+2c-1 D.-(x-y)-4(x+y)=-x-y-4x+4y
⒊ 如果在数轴上表示a、b两个数的点的位置如图所示,
a 0 b
那么化简|a-b|+|a+b|的结果等于 ( )
A.2a B.-2a C.0 D.2b
【深入练习】
⒋去括号:(1)-5a-(4x-6)=______________. (2)-(x-y)+7(m+1)=______________.
⒌化简: (1) 7m-3(m-2n)=______________.
(2)-(x2-y2)—4(x2-y2)=___________.
⒍在括号内填入适当的代数式:(1) x-(___________)=x-2y+1.
(2)1+2ab-a2-b2=1-(_______________).
⒎先去括号,再合并同类项:
(1)-3+(-x2-4x)-(8-3x+3x2) (2) 3(2a2-ab)-2(3a2+ab)
(3) 2a2-{-3a-[4a2-(3a2-a)+(a-a2)]}
8.化简求值:
(1) (x2-2xy+y2)-2(x2-3xy+4y2)+8y2,其中x=-2,y=;
(2) (m-n)+(m+n)+(m+n)-(m-n),其中m=-9,n=-3.
【拓展延伸】
⒐已知:x-2y=5,求下列各式的值:(1)-x+2y;(2)3x-6y;(3)1-4x+8y.
10. 某超市牙膏5元一盒,牙刷2元一枝,现举办促销活动,有两种优惠方式:第一种优惠方式为买一盒牙膏送一枝牙刷,第二种优惠方式为总价打8折.小明准备买x盒牙膏、y枝牙刷(x<y),按两种优惠方式各应付款多少元?两种优惠方式的差价是多少?
【探究创新】
11.(1) 已知2a+3b=4,3a-2b=15,求10a+2b的值.
(2)已知a2-ab=6,ab-b2=2,求a2-2ab+b2,a2-b2的值.
第三章 用字母表示数
第5节 去括号(第2课时)
【基础演练】
⒈减去2x等于x2-3x-6的多项式是 ( )
A.x2-5x-6 B.x2+5x-6 C.x2-x-6 D.x2+5x-6
⒉长方形一边长为4m+n,另一边比它小m-n,则这个长方形的周长为 ( )
A.4m+n B.8m+2n C.14m+6n D.12m+8n
⒊多项式y3-5y2-2y+1与多项式-y3+5y2+4y的和一定是 ( )
A. 奇数 B.偶数 C.整数 D.无法确定
【深入练习】
⒋ (1)多项式3a2-b2-2ab与-b2-4ab-3a2的差是____________.
(2)比2m2-3m-4的2倍多m2+2m的多项式是_______________.
⒌若m-n=-3,mn=2,则(-5m+2)-5(2mn-n)=____________.
⒍已知A=5a2-2ab+6,B=7ab-8a2-7,则A-2B= .
⒎(1) 2(__________)-x2+2=3x2-6;
(2) 5m2-3m+1=(m2+m-2)+(____________).
【拓展延伸】
⒏计算:
(1) 5(x+y)-4(3x-2y)+3(2x-3y) (2) 4a2b-[3ab2-2(3a2b+ab2)]+ab2
⒐已知A=a2+b2-c2,B=-4a2+2b2+3c2,若A+B+C=0,求C.
10. 化简求值:
(1) 2xy-(4xy-8x2y2)+2(3xy-5x2y2),其中x=,y=-.
(2)2(2m+n)2+8(2m+n)-7(2m+n)2-3(2m+n)的值,其中m=-,n=.
11.已知(a+2)2+|a+b+5|=0,求3a2b-[2a2b-(2ab-a2b)-4a2]-ab的值.
12.小红在计算一个整式减去多项式-3a2b+4ab-1时,由于粗心误把减号当成了加号,结果得到-a2b+ab-5.
(1) 请你求出这个整式;(2)求出正确的计算结果.
【探究创新】
13.如图所示的门框,上部是半圆形,下部是长方形,用4根长分别为a+b的可弯折的木条能制作出这样的门框吗?剩余或缺少多长(不计接缝)?
第三章 用字母表示数
单元复习小结
【基础演练】
⒈下列说法正确的是 ( )
A. a是代数式,1不是代数式
B. 表示a,b,的积的代数式为ab
C.用代数式n+1表示人数时,n可以是任意整数
D. a,b两数差的平方与a,b两数积的4倍的和表示为 (a-b)2+4ab
⒉数学课上,赵老师编制了一个程序,当输入任一个有理数时,显示屏上的结果总是所输入的有理数的平方与1的差的2倍.若输入-1,并将显示的结果再次输入,这时显示的结果是 ( )
A. 0 B. -1 C. -2 D. -4
⒊下列说法中正确的是 ( )
A. 单项式的系数是-3
B. -32是单项式,但不是整式
C. πxy,0, y, 3.4╳104, x2-y2都是整式
D. 多项式x2-2xy+4是由x2,2xy,4三项组成的
⒋把2(a+b) -5(b+a)+a+b合并同类项等于 ( )
A.a-b B. -a+b C. 2(a+b) D. -2(a+b)
⒌下列各式中正确的是 ( )
A. -3(a-7)=-3a+7 B. 3a -(4a2+2)=3a-4a2 + 2
C. -[-(2a-3y)]=2a-3y D. -2x-y = -(2x-y)
【深入练习】
⒍已知kx5yn与3x2m+1y3n-2是同类项, 且和为0,则3m-4n+k= .
⒎如图:
(1)这个图形的周长是 .
(2)当a=8.5,b=20时,图形的周长是 .
⒏若x2+3x+5的值等于7,则代数式3x2+9x-2的值等于 .
⒐在计算多项式M加上x2-3x+7时,因误认为加上x2+3x+7,得答案是15x2+2x-4,
则M= ,这个问题的正确答案为 .
⒑当k= 时,代数式(x2-3kxy-3y2)+(xy-8)中不含xy项.
【拓展延伸】
11.当 时,求代数式 的值.
12.已知|a+1|+(b+3)2+|2c-4|=0,求a2b-[a2b-(3abc-a2c)-4a2c]-3abc的值.
13.车间1月份生产x个零件,2月份产量比1月份增加25%,3月份的产量是2月份产量的1.5倍还多10个,设第一季度的产量为y.
(1) 用x代数式表示y.
(2) 当x=48时,求第一季度的产量是多少
【探究创新】
14.以下是用火柴棒搭成的平面图形:
· ·
· ·
· ·
① ② ③
(1)填写下表:
(2)照这样的规律搭下去,第n个图形需要多少根火柴棒?
第三章达标测试卷
一、选择题(每题3分,共15分)
⒈下列各组中的两项,不是同类项的是 ( )
A. 5x2y和-2xy2 B. -1和-42 C.-3xy和yx D. 6a3b4和 -6b4a3
⒉下列各题,合并同类项结果正确的是 ( )
A.2x+3y=5xy B.5x2-x2=4 C.-5mn-5mn=0 D. 9a-7a=2a
⒊下列各式中错误的是 ( )
A. 5a2-(2c-d)=5a2 -2c+d B. x -y= -(y -x)
C. 2(-a+)=-2a+ D. -2(x -1)=-2x+2
⒋已知-x+2y=6,则3(x-2y)2+10y-5x+6的值是 ( )
A. 84 B. 144 C. 72 D. 360
⒌当3≤m<5时,化简|2m-10|-|m-3|得 ( )
A.13+3m B.13-3m C. m-7 D. m-13
二、填空题(每题3分,共15分)
⒍联系实际背景说说代数式4a+3b的意义: .
⒎已知代数式x3m-1y3与x5y2n+1是同类项,则5m+3n的值= .
⒏代数式3-(x-2)2 , 当x= 时有最大值,这个最大值为 .
⒐某公园的成人门票票价是20元,儿童票价是8元,甲旅行团有成人x名和儿童y名,乙旅行团的成人数是甲旅行团的2倍,儿童数是甲旅行团的,两个旅行团门票费用总和
为 元.
⒑已知a2+2ab=-10,b2+2ab=16,则a2+4ab+b2= ,a2-b2= .
三、解答题(11题24分,12题24分,13题12分,14题10分, 共70分)
⒒计算:
(1) -5(a2-2)+4a-8+6(a2-2a) (2) x2-2(x2-xy+y2)+(-x2+3xy+2y2)
(3)3a2b-[4ab2-5(ab2-a2b)+ab2]+a2b
⒓(1) 化简,求值:(-4x2+2x-8)-(x-1),其中x=.
(2) 已知:(x+1)2+|y+2|+4|z+3|=0时,求代数式(2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3)的值.
(3) 设A=a2+ab+b2,B=2a2-ab+2b2,当a=-,b=-2时,求代数式2A-[(2A-B)-2(A-B)]的值.
⒔已知三角形的周长是22厘米,第一条边长为(a+2b)cm,第二条边比第一条边的长多(b+2)cm.
(1) 计算这个三角形的第三条边的长度(用代数式表示).
(2) 当a=3,b=1,第三条边上的高h=8cm时,求这个三角形的面积.
【探究创新】
14.已知代数式2x2+ax-y+6-2bx2+3x-5y-1的值与字母x的取值无关,求a3-2b2-a3+3b2的值.
七(上)数学期中模拟测试
姓名 班级 学号 评价
(试卷满分120分,考试时间120分钟)
一、填上你最有把握的答案,相信你是最棒的!(每空2分,共20分)
1、如果收入100元记作+100元,那么-400元意义是 。
2、、某冷库的温度是-20°C,升高8°C后,再下降6°C,两次变化后的温度是
°C。
3、在数轴上,到表示-2的点距离等于3个单位长度的点所表示的数是 。
4、写出一个系数等于,且只含x、y两个字母的三次单项式 。
5从数-6,1,-3,5,-2中任取三个数相乘,则其积最小的是 。
6、如果x=2,y=,那么代数式 的值是 。
7、小红和小明在玩一种计算游戏,计算的规则见右图, 现在轮到小红计算了,小红输入4 ,请你帮小红算一算,输出结果为 。
8、据生物学统计,一个健康的女子体内每毫升血液中红细胞的数量约为420万个,用科学计数法可表示为_________ (单位:个)
9、3个同学通电话进行交流,每两个同学间要相互通一次话,则他们一共通了 次电话。n个同学间要通 次电话。
二、陷阱好多,要细心哦!比比谁的命中率高(每小题3分,共30分)
10、比–1小1的数是( )
A、–1 B、–2 C、1 D、0
11.四位同学画数轴如下图所示,你认为正确的是( )
A B
C D
12下面关系中,( )是正确的。
A. B. C. D.
13.一块蛋糕,一只小猴第一天吃了一半,第二天吃了剩下的一半,第三天又吃了剩下的一半,第四天这只小猴又吃了剩下的一半,则第四天这只小猴吃了这块蛋糕的( )
A . B. C . D.
14.在(-1)5,(-1)10,-22,(-3)2这四个数中,最大的数比最小的数要大( )
A. 8 B. 10 C. 13 D. 5
15、如果a<0,那么下列各式中一定为负数的是( )
A、-a B、 C、1-a D、-(-a)-1
16.如果-23ab2m与-2ma2nb4是同类项,则m+n=( )
A. B.2 C. D.
17、单项式-23ab的系数是__________,次数是__________。( )
A、系数是-23,次数是2次 B、系数是-2,次数是6次
C、系数是-6,次数是3次 D、系数是-8,次数是3次
18、“神州六号” 载人宇宙飞船在天空中运行的轨道近似为圆形,轨道半径约为6700千米,请计算(可以用计算器)“神州六号”在天空中飞行77圈共飞行了 (π取3.14)
( )
A. 4.2万千米 B.51.6万千米
C. 162万千米 D.324万千米
19、张明的学校、家、书店依次坐落在一条南北走向的大街上,学校在家的南边20米,书店在家北边100米,张明从家里出发,向北走了50米,接着又向南走了70米,此时张明的位置在……………( )
A.学校 B.家 C.书店 D.不在上述地方
三、仔细读题,看谁把数轴画的准确而又漂亮。(本题6分)
20、在数轴上画出表示数的点,并把这组数从小到大用“<”连接起来。
四、看谁算得又快又正确,并会写出计算过程。
21、计算(16分):
(1).(-1)-(-1+) (2). -8÷2÷(-)×(-)
(3).-14-(-1)2005-(--)×24+∣-32+5∣
(4)
22、(8分)化简:
(1)
(2)2a2b3-3[a3b2-2(4a2b3-a3b2)]+(-1)5b3a2
23、(6分)你知道吗?先化简再求值可使解题简便多了!你是如何解决下列问题的?
已知x=,y=-, 求代数式 -4(y-2x)-3x-6y+5的值.
五、生活中处处存在着数学,你考虑过下列问题吗 不妨一试.
24、(8分)按如下方式摆放餐桌和椅子:
(1)如图,一张桌子可以坐6个人;两张桌子可以坐8个人
(2)三张桌子可以坐_______个人
(3)按照这种摆放10张桌子,可以坐__________个人
按照这种摆放n张桌子,可以坐___________个人。
(4)如果要安排全班50名同学入坐,需要多少张桌子?
25.(8分)淮河入海道警戒水位是8.5m,以下是淮河入海管理站七月份某周监测到的水位变化情况(上周末已达警戒水位)
星 期 一 二 三 四 五 六 日
水位变化/m(与前一天比较) +0.25 +0.15 +0.3 +0.4 -0.1 +0.2 -0.35
(1) 分别计算本周一、二的水位高度,并由此得出周二比周一的水位是高还是低?
(2)该周星期几的水位最高?最高为多少?(4分)
26、(8分)某商店积压了100件某种商品,为使这些货物尽快脱手,该商店采取了如下销售方案,先将价格提高到原价的2.5倍,再作三次降价处理:第一次降价20%,标出“亏本价”;第二次在“亏本价”的基础上降价30%,标出“破产价”;第三次在“破产价”的基础上再降价40%,标出“跳楼价”。三次降价处理销售结果如下表:
降价次数 一 二 三
销售件数 20 40 一抢而光
问:(1)跳楼价占原价的百分比是多少?
(2)假设原价为a元,该商品按新销售方案销售,相比原价全部售完,哪一种方案盈利最大?最大为多少?
六、我是聪明的,我能解决(本题10分)
27.阅读理解:
(1)阅读下面材料:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为。
点A、B两点中有一点在原点时,不妨设点A在原点,如图1,;当A、B两点都不在原点时,
1 如图2,点A、B都在原点的右边,
2 如图3,点A、B都在原点的左边,
3 如图4,点A、B在原点的两边,
。
综上,数轴上A、B两点之间的距离。
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是____________,数轴上表示-2和-5的两点之间的距离是___________,数轴上表示1和-3的两点之间的距离是___________;
②数轴上表示x和-1的两点A和B之间的距离是___________,如果,那么x为_____________;
③如果代数式取得最小值4,请你写出一个能使上式取得最小值的x的值。
完成了,真开心,对了要检查一下!
火柴棒的根数
图形编号
①
②
③
……
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
否
是
b
a
输出
>10
+5
×2
b
a
输入x
第1节 用字母表示数
【基础演练】
⒈买单价为a元的温度计n个,付出b元,应找回钱数是 ( )
A.(b-a)元 B.(b-n)元 C.(na-b)元 D.(b-na)元
⒉一个两位数,十位上的数字为a,个位上的数字比十位上的数字的一半多5,那么这个两位数是 ( )
A.10a+(+5) B.10a+(-5) C.10a+(2a-5) D.10a+(2a-10)
⒊已知长方形的周长是m厘米,一边长为a厘米,则这个长方形的面积是 ( )
A.平方厘米 B.(—a)平方厘米
C.a(—a)平方厘米 D.平方厘米,
⒋第二十届电视剧飞天奖今年有a部作品参赛,比去年增加了40℅还多2部,设去年参赛的作品有b部,则b是 ( )
A. B. C.a(1+40%)+2 D.a(1+40%)-2
【深入练习】
⒌某工厂一月份生产机床m台,二月份比一月份增产10%,则二月份生产机床 台,
⒍某商品8折优惠售价为x元,则原价是 元.
⒎ 三个连续的偶数,中间一个是n. 则其余两个分别是 、 .
⒏ 汽车的速度是v米/秒,火车的速度比汽车的速度的2倍少15米/秒,则火车的速度
是 米/秒.
⒐ 观察下列各式:
1×3=1+2×1 2×4=2+2×2 ………
3×5=3+2×3 4×6=4+2×4
请你将猜想到的规律用正整数n(n≥1) 表示出来 .
10.将一个边长为1的正方形分成两个相同的矩形,再将其中的一个矩形分成两个相同的矩形……以此类推不断地分下去,不用通分,观察图形你能一下子计算出下式的结果吗
.
【拓展延伸】
11. 如图已知正方形的边长为a,求阴影部分的面积.
12.用黑白两种颜色的正六边形地面砖按下所示的规律拼成若干个图案,
第一个 第二个 第三个
⑴第四个图案中有白色的地面砖 块,
⑵第n个图案中有白色的地面砖 块.
13.3个球队进行单循环比赛(参赛的每个队都与其他队赛一场),总的比赛场数是多少?4个球队呢?写出m个球队进行单循环比赛时总的比赛场数n的公式.
【探究创新】
14.有若干个数,第1个数记为,第2个数记为,第3个数记为,……第n个数记为,若,从第2个数起,每一个数都等于“1与它前面的那个数的差的倒数”则① ,= , ;
②根据以上结果可知: , .
第三章 用字母表示数
第2节 代数式(第1课时)
【基础演练】
⒈下列式子中符合代数式的书写格式的是 ( )
A.x·20y B.2÷ab C.(a-b)千克 D.2mn千米
⒉下列说法正确的是 ( )
A.0、b、都是整式 B.单项式a没有系数
C.没有加减运算的代数式是单项式
D.x—2xy—y是由x、—2xy、—y三项组成.
⒊设甲数为a,甲数比乙数小20%,用代数式表示乙数 ( )
A.a-20% B.(1-20%)a C.(1+20%)a D.
⒋某校阶梯教室第一排有m个座位,后面每排比前一排多2个座位,则第n排的座位数
是 ( )
A.m+2n B.mn+2 C.m+2(n—1) D.m+(n+2)
⒌一家三口准备外出旅游,甲乙两家的旅行社的报价相同,为了竞争,甲旅行社说:“父亲买全票,其它人可享受6折优惠”.乙旅行社说:“家庭旅行可按团体票计价,按原价的优惠”,由此可以判断 ( )
A.甲比乙优惠 B.乙比甲优惠 C.甲乙收费相同 D.以上都有可能
⒍如图用火柴棒搭正方形,甲、乙、丙、丁四位同学都用x表示所搭正方形的个数,从而计算火柴棒的根数,他们计算的结果分别是:
甲:4+3(X-1); 乙:x+x+(x+1);
丙:1+3x; 丁:4x-(x-1).
其中计算结果正确的同学有 ( )
A.1位 B.2位 C.3位 D.4位
【深入练习】
⒎若n为正整数,用代数式表示:
1 中间一个数为n的三个连续整数为 .
2 与2n相邻的奇数为 .
3 最大的一个是2n+2的三个连续的偶数 .
⒏某车间第一年的产值为a万元,第二年的产值增加x%,第三年的产值又比第二年增加x%,则第三年的产值为 万元,
⒐代数式-是______次单项式,系数为________.
⒑托运行李p千克(p为整数)的费用标准:已知托运第1个1千克需付2元,以后每增加1千克(不足1千克按1千克计)需增加费用5角.若某人托运p千克(p>1)的行李,则托运费用为 .
【拓展延伸】
⒒用代数式表示下列各题:
①比x的3倍大6的数, ②比x小6的数的三分之一,
③a、b两数的和与a、b两数差的积, ④被5除商为n余3的数,
⒓某种商品每件的成本为5元,售价比成本高10%,如果售了a件,那么销售总额为b元,用a的代数式表示b.
⒔一个三位数,它的十位上的数字是百位上数字的3倍,个位上的数字是百位上数字的2倍.设这个三位数个位上的数字是x,十位上的数字为y,百位上的数字为z.
(1)用含x、y、z的代数式表示这个三位数 ;
(2)用含z的代数式表示这个三位数 ;
(3)写出所有满足题目条件的三位数 .
【探究创新】
⒕学校组织学生到距离学校6km的光明科技馆去参观,学生李明因事没能乘上学校的包车,于是准备在校门口乘出租车去光明科技馆,出租车收费标准如下:
里程 收费∕元
3km以下(含3km) 8.00
3km以上(每增加1km) 1.80
⑴若出租车行驶的里程为xkm(x>3)请用x的代数式表示车费y元.
⑵李明身上仅有14元钱,够不够支付乘出租车到科技馆的车费?
请说明理由.
第三章 用字母表示数
第3节 代数式的值(第1课时)
【基础演练】
⒈当x=-1时,代数式|5x+2|和1-3x的值分别为M、N,则M、N之间的关系为 ( )
A.M>N B. M<N C. M=N D. 以上答案都有可能
⒉当a=-2时,代数式-a2的值是 ( )
A.4 B.-2 C.-4 D.2
⒊已知a-b=-2,则代数式3(a-b)2-b+a的值为 ( )
A. 10 B. 12 C. -10 D.-12
⒋小王利用计算机设计了一个计算程序,输入与输出的数据如下表:
输入 1 2 3 4 5 …
输出 …
当输入数据8时,输出的数据是 ( )
A. B. C. D.
【深入练习】
⒌已知:x=-1,y=2, 则(x-y)2-x3+x2y2 = .
⒍已知:a=,b=,则a2-2ab+b2= .
⒎当m-n=5, mn= -2,则代数式(n-m)2-4mn= .
⒏已知:x2+xy=1,xy-y2=-4,则x2+2xy-y2= .
⒐若m2+3n-1的值为5,则代数式2m2+6n+1的值为 .
10. 则代数式的值为 .
【拓展延伸】
11. 若(a+3)2+|b-4|=0分别求下列代数式的值:
(1) (a+b) -(a-b)2 (2) 2a-3b + a2+2b2
12.经批准,某商品的价格可在定价的基础上根据市场行情最多上浮20%,最多下浮30%.
(1) 若这种商品定价为a元,那么这种商品的售价可以在什么范围内?
(2) 若定价为100元,那么售价可在什么范围内?
13.按图示的计算程序计算并填写下表:
输入 0 0.3 3
输出
【探究创新】
14.当a=-0.5,b=0.25时,求下列代数式的值:
(1) (a+b)2 (2) a2+2ab+b2
(3) 回答下问题:
①这两个代数式的值有什么关系?
②当a=2,b=-3时,上述结论是否仍然成立?
③再自选一组a、b的值试一试.
④你能用简便的方法算出当a=-0.875,b=-0.125时,代数式a2+2ab+b2的值吗?
第三章 用字母表示数
第3节 代数式的值(第2课时)
【基础演练】
⒈右图所示是一个数值转换机,输入x,输出3(x-1),下面给出了四种转换步骤,其中不正确的是 ( )
A.先减去1,再乘以3
B.先乘以3,再减去1? 输入x 输出3(x-1)
C.先乘以3,再减去3
D.先加上-1,再乘以3
⒉下列代数式的值一定是正数的是 ( )
A.(a+1)2 B.|x+3| C.1+(-b)2 D.1-(-y)2
⒊已知a、b互为相反数,c、d互为倒数,|m|=2,则代数式110(a+b)2+3cd-的值为 ( )
A.2 B.3 C.4 D.5
⒋若x=3a,y=3x,则x-y+a等于 ( )
A.a B.10a C.-5a D.-a
⒌若时,代数式的值为5,则时,代数式的值等于( )
A .0 B.-3 C.-4 D.-5
【深入练习】
⒍华氏温度f和摄氏温度c的关系是:f=c+32,当人的体温为37度时,华氏温度
为 度.
⒎甲每天可做x个零件,乙每天可做y个零件,两人同时工作共做m个零件,需要的时间为 天,若x=25,y=30,m=385,则两人需 天完成任务.
⒏某百货商厦元月份的销售额为a元,二月份比元月份的销售额多b元,三月份比二月份减少10%,则第一季度的销售额总计为 元.当a=30000,b=5000时,第一季度的总销售额为 元.
⒐某市为鼓励市民节约用水,对自来水用户按如下标准收费:若每月用户用水不超过20m3,则每立方米按x元收费;若超过20 m3,则超过的部分按y元收费;若居民在一个月内用水35 m3,则他该月应缴水费 元.
【拓展延伸】
10.填写下表,并观察下列两个代数式的值的变化.
x 1 2 3 4 5 6 ……
-2x-6
-x2
估计一下,哪个代数式的值会先小于-100?
11.生物学家发现,气温y在一定温度内时,某地种蟋蟀每分钟鸣叫的次数x与气温y(单位:℃)有一定的关系,下表是通过实验得到的一组数据:
x(次/分) 20 30 40 50 60 …
y(℃) 25 25+2.5 25+5 25+7.5 25+10 …
(1)根据表中的数据,写出y与x之间的关系式
(2)当这种蟋蟀每分钟鸣叫56次时,该地当时的气温多少
【探究创新】
12. 你能比较两个数的大小吗?
为了解决这个问题,我们首先把它抽象成一般开工,即比较的大小(n为自然数),我们从分析特殊向简单的情形入手,n=1,n=2,n=3,…的分析,从中发现规律,经过归纳,猜想出结论.
(1)计算,比较下列各组数中两个数大小(在空格中填“>”、“=”、“<”)
2, , , , ,…
(2)从上面的结果进行归纳猜想,的大小关系是 .
(3)根据上面的归纳猜想出一般结论,试比较的大小.
第三章 用字母表示数
第4节 合并同类项(第1课时)
【基础演练】
⒈下列各组式子中,是同类项的是 ( )
A. 3x2y和-3xy2 B. 5ab和-7bac C. 2x2和2x3 D. 23和-15
⒉下列合并同类项正确的是 ( )
A. 5m2n-3m2n =2 B. 2a2+3a4=5a6
C. -x2-x2-x2=-3x2 D. -ab-ab=0
⒊多项式7a2-6a3b+3a2b+3a2+6a3b-3a2b-10a2的值 ( )
A. 与字母a,b都有关 B. 只与字母a有关
C. 只与字母b有关 D. 与字母a,b都无关
【深入练习】
⒋若单项式xm+1y2与-x3yn-1是同类项,则m=________, n=________.
⒌三个连续的奇数中,最小的一个是2n-1,则这三个连续奇数的和为________.
⒍七年级(9)班给“希望工程”捐款x元,七年级(1)班比(9)班多10元,七年级(8)班捐的钱是(9)班的2倍少30元,这3个班共捐款__________元
【拓展延伸】
7.合并同类项:
(1) 5ab2-7a2b-8ab2-3a2b
(2) x2y2-3xy-7x2y2+xy-1+5x2y2
(3)(m+2n)2-5(m-n)-(m+2n)2 +3(m-n)
8. 已知、满足|-1|+(3+2-7)2=0,有下列单项式:(1);
(2);(3) .试判断其中是否有同类项?若有,请指出.
9.求代数式的值:2x2-5xy+2y2-x2-xy-2y2-3x2+5,其中x=-1,y=-.
10.已知t=-,求代数式2(t2-t-1)-(t2-t-1)+3(t2-t-1)的值.
11.某商场1月份销售额a万元,2月份销售额比1月份增长10%,3月份比前两个月的和少a万元,求该商场第一季度总销售额. 若a=100,求第一季度总销售额是多少万元?
【探究创新】
12.若多项式的值与无关,求的值.
第三章 用字母表示数
第4节 合并同类项(第2课时)
【基础演练】
⒈下列各组代数式中,不是同类项的是 ( )
A. B. C. D.
⒉下列合并同类项正确的是 ( )
A. B.
C. D.
⒊已知则多项式的值为 ( )
A.-1 B. C.1 D.
⒋已知多项式ax+bx合并后结果为零,则下列说法正确的是 ( )
A.a=b=0 B.a=b=x=0 C.a+b=0 D.a-b=0
⒌已知是同类项,则代数式的值是 ( )
A.-1 B.0 C.1 D.无法求得
【深入练习】
⒍当m= ,n= 时,和是同类项
⒎三角形的三边长分别为5x,12x,13x,则这个三角形的周长为 ,当x=2cm时,周长为 cm.
⒏合并同类项: .
【拓展延伸】
⒐合并同类项:
(1)
(2)
10.求下列各式的值:
(1) 2x2y-3xy+x2-2x2y+5xy-x2,其中x=4,y=-3.
(2) ,其中
11.已知:x2+y2=7,xy=-2. 求5x2-3xy-4y2-11xy-7x2+2y2的值.
【探究创新】
12.在“计算4a2-2ab+3b-a2+2ab-5-3a2的值,其中a=-,b=3 ”的解题过程中,小芳把a=-错写成a=,小华错写成a=.但他们的答案都是正确的,你知道这是什么原因吗?
第三章 用字母表示数
第5节 去括号(第1课时)
【基础演练】
⒈下列式子中,去括号后得a-b+c的是 ( )
A. a-(b+c) B. -(a-b)+c C. a-(b-c) D. -(a+b)+c
⒉下列去括号中正确的是 ( )
A.a2-(2a-b+c)=a2-2a-b+c B.x2+3(x-1)=x2+3x-1
C.3m-[5b-(2c-1)]=3a-5b+2c-1 D.-(x-y)-4(x+y)=-x-y-4x+4y
⒊ 如果在数轴上表示a、b两个数的点的位置如图所示,
a 0 b
那么化简|a-b|+|a+b|的结果等于 ( )
A.2a B.-2a C.0 D.2b
【深入练习】
⒋去括号:(1)-5a-(4x-6)=______________. (2)-(x-y)+7(m+1)=______________.
⒌化简: (1) 7m-3(m-2n)=______________.
(2)-(x2-y2)—4(x2-y2)=___________.
⒍在括号内填入适当的代数式:(1) x-(___________)=x-2y+1.
(2)1+2ab-a2-b2=1-(_______________).
⒎先去括号,再合并同类项:
(1)-3+(-x2-4x)-(8-3x+3x2) (2) 3(2a2-ab)-2(3a2+ab)
(3) 2a2-{-3a-[4a2-(3a2-a)+(a-a2)]}
8.化简求值:
(1) (x2-2xy+y2)-2(x2-3xy+4y2)+8y2,其中x=-2,y=;
(2) (m-n)+(m+n)+(m+n)-(m-n),其中m=-9,n=-3.
【拓展延伸】
⒐已知:x-2y=5,求下列各式的值:(1)-x+2y;(2)3x-6y;(3)1-4x+8y.
10. 某超市牙膏5元一盒,牙刷2元一枝,现举办促销活动,有两种优惠方式:第一种优惠方式为买一盒牙膏送一枝牙刷,第二种优惠方式为总价打8折.小明准备买x盒牙膏、y枝牙刷(x<y),按两种优惠方式各应付款多少元?两种优惠方式的差价是多少?
【探究创新】
11.(1) 已知2a+3b=4,3a-2b=15,求10a+2b的值.
(2)已知a2-ab=6,ab-b2=2,求a2-2ab+b2,a2-b2的值.
第三章 用字母表示数
第5节 去括号(第2课时)
【基础演练】
⒈减去2x等于x2-3x-6的多项式是 ( )
A.x2-5x-6 B.x2+5x-6 C.x2-x-6 D.x2+5x-6
⒉长方形一边长为4m+n,另一边比它小m-n,则这个长方形的周长为 ( )
A.4m+n B.8m+2n C.14m+6n D.12m+8n
⒊多项式y3-5y2-2y+1与多项式-y3+5y2+4y的和一定是 ( )
A. 奇数 B.偶数 C.整数 D.无法确定
【深入练习】
⒋ (1)多项式3a2-b2-2ab与-b2-4ab-3a2的差是____________.
(2)比2m2-3m-4的2倍多m2+2m的多项式是_______________.
⒌若m-n=-3,mn=2,则(-5m+2)-5(2mn-n)=____________.
⒍已知A=5a2-2ab+6,B=7ab-8a2-7,则A-2B= .
⒎(1) 2(__________)-x2+2=3x2-6;
(2) 5m2-3m+1=(m2+m-2)+(____________).
【拓展延伸】
⒏计算:
(1) 5(x+y)-4(3x-2y)+3(2x-3y) (2) 4a2b-[3ab2-2(3a2b+ab2)]+ab2
⒐已知A=a2+b2-c2,B=-4a2+2b2+3c2,若A+B+C=0,求C.
10. 化简求值:
(1) 2xy-(4xy-8x2y2)+2(3xy-5x2y2),其中x=,y=-.
(2)2(2m+n)2+8(2m+n)-7(2m+n)2-3(2m+n)的值,其中m=-,n=.
11.已知(a+2)2+|a+b+5|=0,求3a2b-[2a2b-(2ab-a2b)-4a2]-ab的值.
12.小红在计算一个整式减去多项式-3a2b+4ab-1时,由于粗心误把减号当成了加号,结果得到-a2b+ab-5.
(1) 请你求出这个整式;(2)求出正确的计算结果.
【探究创新】
13.如图所示的门框,上部是半圆形,下部是长方形,用4根长分别为a+b的可弯折的木条能制作出这样的门框吗?剩余或缺少多长(不计接缝)?
第三章 用字母表示数
单元复习小结
【基础演练】
⒈下列说法正确的是 ( )
A. a是代数式,1不是代数式
B. 表示a,b,的积的代数式为ab
C.用代数式n+1表示人数时,n可以是任意整数
D. a,b两数差的平方与a,b两数积的4倍的和表示为 (a-b)2+4ab
⒉数学课上,赵老师编制了一个程序,当输入任一个有理数时,显示屏上的结果总是所输入的有理数的平方与1的差的2倍.若输入-1,并将显示的结果再次输入,这时显示的结果是 ( )
A. 0 B. -1 C. -2 D. -4
⒊下列说法中正确的是 ( )
A. 单项式的系数是-3
B. -32是单项式,但不是整式
C. πxy,0, y, 3.4╳104, x2-y2都是整式
D. 多项式x2-2xy+4是由x2,2xy,4三项组成的
⒋把2(a+b) -5(b+a)+a+b合并同类项等于 ( )
A.a-b B. -a+b C. 2(a+b) D. -2(a+b)
⒌下列各式中正确的是 ( )
A. -3(a-7)=-3a+7 B. 3a -(4a2+2)=3a-4a2 + 2
C. -[-(2a-3y)]=2a-3y D. -2x-y = -(2x-y)
【深入练习】
⒍已知kx5yn与3x2m+1y3n-2是同类项, 且和为0,则3m-4n+k= .
⒎如图:
(1)这个图形的周长是 .
(2)当a=8.5,b=20时,图形的周长是 .
⒏若x2+3x+5的值等于7,则代数式3x2+9x-2的值等于 .
⒐在计算多项式M加上x2-3x+7时,因误认为加上x2+3x+7,得答案是15x2+2x-4,
则M= ,这个问题的正确答案为 .
⒑当k= 时,代数式(x2-3kxy-3y2)+(xy-8)中不含xy项.
【拓展延伸】
11.当 时,求代数式 的值.
12.已知|a+1|+(b+3)2+|2c-4|=0,求a2b-[a2b-(3abc-a2c)-4a2c]-3abc的值.
13.车间1月份生产x个零件,2月份产量比1月份增加25%,3月份的产量是2月份产量的1.5倍还多10个,设第一季度的产量为y.
(1) 用x代数式表示y.
(2) 当x=48时,求第一季度的产量是多少
【探究创新】
14.以下是用火柴棒搭成的平面图形:
· ·
· ·
· ·
① ② ③
(1)填写下表:
(2)照这样的规律搭下去,第n个图形需要多少根火柴棒?
第三章达标测试卷
一、选择题(每题3分,共15分)
⒈下列各组中的两项,不是同类项的是 ( )
A. 5x2y和-2xy2 B. -1和-42 C.-3xy和yx D. 6a3b4和 -6b4a3
⒉下列各题,合并同类项结果正确的是 ( )
A.2x+3y=5xy B.5x2-x2=4 C.-5mn-5mn=0 D. 9a-7a=2a
⒊下列各式中错误的是 ( )
A. 5a2-(2c-d)=5a2 -2c+d B. x -y= -(y -x)
C. 2(-a+)=-2a+ D. -2(x -1)=-2x+2
⒋已知-x+2y=6,则3(x-2y)2+10y-5x+6的值是 ( )
A. 84 B. 144 C. 72 D. 360
⒌当3≤m<5时,化简|2m-10|-|m-3|得 ( )
A.13+3m B.13-3m C. m-7 D. m-13
二、填空题(每题3分,共15分)
⒍联系实际背景说说代数式4a+3b的意义: .
⒎已知代数式x3m-1y3与x5y2n+1是同类项,则5m+3n的值= .
⒏代数式3-(x-2)2 , 当x= 时有最大值,这个最大值为 .
⒐某公园的成人门票票价是20元,儿童票价是8元,甲旅行团有成人x名和儿童y名,乙旅行团的成人数是甲旅行团的2倍,儿童数是甲旅行团的,两个旅行团门票费用总和
为 元.
⒑已知a2+2ab=-10,b2+2ab=16,则a2+4ab+b2= ,a2-b2= .
三、解答题(11题24分,12题24分,13题12分,14题10分, 共70分)
⒒计算:
(1) -5(a2-2)+4a-8+6(a2-2a) (2) x2-2(x2-xy+y2)+(-x2+3xy+2y2)
(3)3a2b-[4ab2-5(ab2-a2b)+ab2]+a2b
⒓(1) 化简,求值:(-4x2+2x-8)-(x-1),其中x=.
(2) 已知:(x+1)2+|y+2|+4|z+3|=0时,求代数式(2x3-xyz)-2(x3-y3+xyz)+(xyz-2y3)的值.
(3) 设A=a2+ab+b2,B=2a2-ab+2b2,当a=-,b=-2时,求代数式2A-[(2A-B)-2(A-B)]的值.
⒔已知三角形的周长是22厘米,第一条边长为(a+2b)cm,第二条边比第一条边的长多(b+2)cm.
(1) 计算这个三角形的第三条边的长度(用代数式表示).
(2) 当a=3,b=1,第三条边上的高h=8cm时,求这个三角形的面积.
【探究创新】
14.已知代数式2x2+ax-y+6-2bx2+3x-5y-1的值与字母x的取值无关,求a3-2b2-a3+3b2的值.
七(上)数学期中模拟测试
姓名 班级 学号 评价
(试卷满分120分,考试时间120分钟)
一、填上你最有把握的答案,相信你是最棒的!(每空2分,共20分)
1、如果收入100元记作+100元,那么-400元意义是 。
2、、某冷库的温度是-20°C,升高8°C后,再下降6°C,两次变化后的温度是
°C。
3、在数轴上,到表示-2的点距离等于3个单位长度的点所表示的数是 。
4、写出一个系数等于,且只含x、y两个字母的三次单项式 。
5从数-6,1,-3,5,-2中任取三个数相乘,则其积最小的是 。
6、如果x=2,y=,那么代数式 的值是 。
7、小红和小明在玩一种计算游戏,计算的规则见右图, 现在轮到小红计算了,小红输入4 ,请你帮小红算一算,输出结果为 。
8、据生物学统计,一个健康的女子体内每毫升血液中红细胞的数量约为420万个,用科学计数法可表示为_________ (单位:个)
9、3个同学通电话进行交流,每两个同学间要相互通一次话,则他们一共通了 次电话。n个同学间要通 次电话。
二、陷阱好多,要细心哦!比比谁的命中率高(每小题3分,共30分)
10、比–1小1的数是( )
A、–1 B、–2 C、1 D、0
11.四位同学画数轴如下图所示,你认为正确的是( )
A B
C D
12下面关系中,( )是正确的。
A. B. C. D.
13.一块蛋糕,一只小猴第一天吃了一半,第二天吃了剩下的一半,第三天又吃了剩下的一半,第四天这只小猴又吃了剩下的一半,则第四天这只小猴吃了这块蛋糕的( )
A . B. C . D.
14.在(-1)5,(-1)10,-22,(-3)2这四个数中,最大的数比最小的数要大( )
A. 8 B. 10 C. 13 D. 5
15、如果a<0,那么下列各式中一定为负数的是( )
A、-a B、 C、1-a D、-(-a)-1
16.如果-23ab2m与-2ma2nb4是同类项,则m+n=( )
A. B.2 C. D.
17、单项式-23ab的系数是__________,次数是__________。( )
A、系数是-23,次数是2次 B、系数是-2,次数是6次
C、系数是-6,次数是3次 D、系数是-8,次数是3次
18、“神州六号” 载人宇宙飞船在天空中运行的轨道近似为圆形,轨道半径约为6700千米,请计算(可以用计算器)“神州六号”在天空中飞行77圈共飞行了 (π取3.14)
( )
A. 4.2万千米 B.51.6万千米
C. 162万千米 D.324万千米
19、张明的学校、家、书店依次坐落在一条南北走向的大街上,学校在家的南边20米,书店在家北边100米,张明从家里出发,向北走了50米,接着又向南走了70米,此时张明的位置在……………( )
A.学校 B.家 C.书店 D.不在上述地方
三、仔细读题,看谁把数轴画的准确而又漂亮。(本题6分)
20、在数轴上画出表示数的点,并把这组数从小到大用“<”连接起来。
四、看谁算得又快又正确,并会写出计算过程。
21、计算(16分):
(1).(-1)-(-1+) (2). -8÷2÷(-)×(-)
(3).-14-(-1)2005-(--)×24+∣-32+5∣
(4)
22、(8分)化简:
(1)
(2)2a2b3-3[a3b2-2(4a2b3-a3b2)]+(-1)5b3a2
23、(6分)你知道吗?先化简再求值可使解题简便多了!你是如何解决下列问题的?
已知x=,y=-, 求代数式 -4(y-2x)-3x-6y+5的值.
五、生活中处处存在着数学,你考虑过下列问题吗 不妨一试.
24、(8分)按如下方式摆放餐桌和椅子:
(1)如图,一张桌子可以坐6个人;两张桌子可以坐8个人
(2)三张桌子可以坐_______个人
(3)按照这种摆放10张桌子,可以坐__________个人
按照这种摆放n张桌子,可以坐___________个人。
(4)如果要安排全班50名同学入坐,需要多少张桌子?
25.(8分)淮河入海道警戒水位是8.5m,以下是淮河入海管理站七月份某周监测到的水位变化情况(上周末已达警戒水位)
星 期 一 二 三 四 五 六 日
水位变化/m(与前一天比较) +0.25 +0.15 +0.3 +0.4 -0.1 +0.2 -0.35
(1) 分别计算本周一、二的水位高度,并由此得出周二比周一的水位是高还是低?
(2)该周星期几的水位最高?最高为多少?(4分)
26、(8分)某商店积压了100件某种商品,为使这些货物尽快脱手,该商店采取了如下销售方案,先将价格提高到原价的2.5倍,再作三次降价处理:第一次降价20%,标出“亏本价”;第二次在“亏本价”的基础上降价30%,标出“破产价”;第三次在“破产价”的基础上再降价40%,标出“跳楼价”。三次降价处理销售结果如下表:
降价次数 一 二 三
销售件数 20 40 一抢而光
问:(1)跳楼价占原价的百分比是多少?
(2)假设原价为a元,该商品按新销售方案销售,相比原价全部售完,哪一种方案盈利最大?最大为多少?
六、我是聪明的,我能解决(本题10分)
27.阅读理解:
(1)阅读下面材料:
点A、B在数轴上分别表示有理数a、b,A、B两点之间的距离表示为。
点A、B两点中有一点在原点时,不妨设点A在原点,如图1,;当A、B两点都不在原点时,
1 如图2,点A、B都在原点的右边,
2 如图3,点A、B都在原点的左边,
3 如图4,点A、B在原点的两边,
。
综上,数轴上A、B两点之间的距离。
(2)回答下列问题:
①数轴上表示2和5的两点之间的距离是____________,数轴上表示-2和-5的两点之间的距离是___________,数轴上表示1和-3的两点之间的距离是___________;
②数轴上表示x和-1的两点A和B之间的距离是___________,如果,那么x为_____________;
③如果代数式取得最小值4,请你写出一个能使上式取得最小值的x的值。
完成了,真开心,对了要检查一下!
火柴棒的根数
图形编号
①
②
③
……
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
否
是
b
a
输出
>10
+5
×2
b
a
输入x
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
