函数模型解决实际问题(第一课时) 课件(共26张PPT)
文档属性
| 名称 | 函数模型解决实际问题(第一课时) 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 12:05:25 | ||
图片预览






文档简介
(共26张PPT)
函数模型及解决实际问题
(澳大利亚兔子数“爆炸”)
1859年,一位叫托马斯·奥斯汀英格兰农场主从欧洲带了十几只兔子到澳洲,由于这位农场主非常爱好狩猎,于是将兔子放养到其领地附近,由于澳洲有茂盛的牧草,而且没有兔子的天敌,兔子数量不断增加,短短几十年时间,兔子们占领了整个澳大利亚,数量达到75亿只.可爱的兔子变得可恶起来,75亿只兔子吃掉了大量的牧草,草原的载畜量大大降低,而牛羊是澳大利亚的主要牲口.这使澳大利亚头痛不已,他们采用各种方法消灭这些兔子,但是效果都不好,直至二十世纪五十年代,科学家采用载液瘤病毒杀死了百分之九十的野兔,澳大利亚人才算松了一口气.
(澳大利亚兔子数“爆炸”)
指数增长
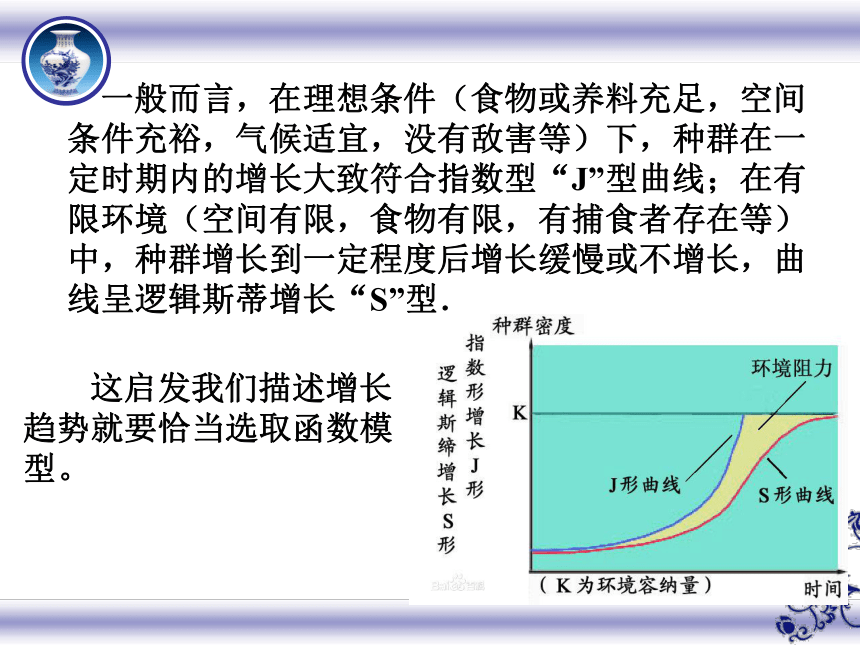
一般而言,在理想条件(食物或养料充足,空间条件充裕,气候适宜,没有敌害等)下,种群在一定时期内的增长大致符合指数型“J”型曲线;在有限环境(空间有限,食物有限,有捕食者存在等)中,种群增长到一定程度后增长缓慢或不增长,曲线呈逻辑斯蒂增长“S”型.
这启发我们描述增长趋势就要恰当选取函数模型。
(线性函数、指数函数和对数函数模型)
生活中几类不同增长的函数模型
第一课时
先定一个能达到的小目标,比方说我先挣它一个亿!
例1:假设你有一笔资金用于投资,现有三种投资方案
供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
你会选择哪种投资方案呢?
分析:
①依据什么标准来选择投资方案
②分析数量关系,归纳概括相应的函数模型,建立函数关系.
回报量
每日回报
累计回报
建立日回报金额与投资天数的函数关系
投资天数
40
40
40
40
40
10
10+10
=10×2
10+10+10
=10×3
10+10+10+10
=10×4
10+10+10+10+10
=10×5
0.4
0.4×2
0.4×2×2
=0.4×22
0.4×2×2×2
=0.4×23
0.4×2×2×2×2
=0.4×24
方案一
方案二
方案三
1
2
3
4
5
则方案一可以用函数________________进行描述;
方案二可以用函数__________________描述;
方案三可以用______________________描述。
解:设第x天的回报是y元,
y=40 (x∈N*)
y=10x (x∈N*)
y=0.4×2x-1 (x∈N*)
常数函数
一次函数
指数型函数
增长情况?
数据表格 图像
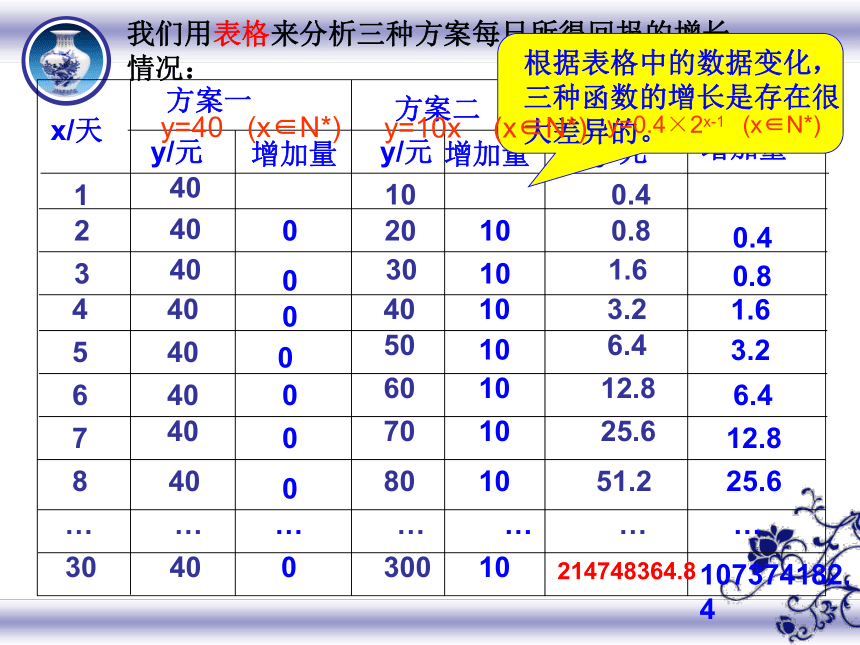
我们用表格来分析三种方案每日所得回报的增长情况:
x/天
方案一
方案二
方案三
y/元
y/元
y/元
增加量
增加量
增加量
1
2
3
40
40
40
0
0
10
20
30
10
10
0.4
0.8
1.6
0.4
0.8
4
5
6
7
8
…
30
…
40
40
40
40
40
40
0
…
0
0
0
0
0
…
40
50
60
70
80
300
…
10
10
10
10
10
10
…
3.2
6.4
12.8
25.6
51.2
…
1.6
3.2
6.4
12.8
25.6
根据表格中的数据变化,三种函数的增长是存在很大差异的。
y=40 (x∈N*)
y=10x (x∈N*)
y=0.4×2x-1 (x∈N*)
214748364.8
107374182.4
o
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
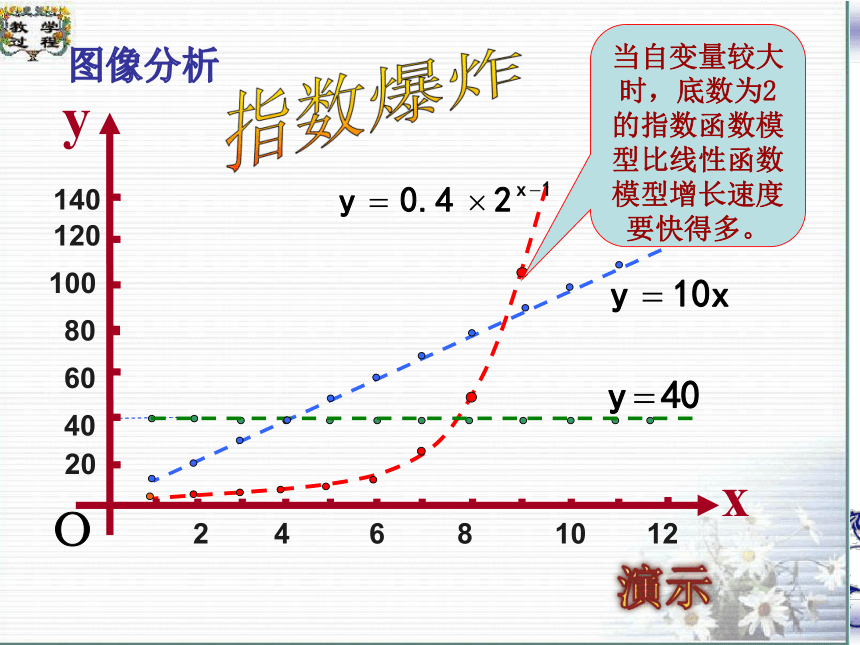
当自变量较大时,底数为2的指数函数模型比线性函数模型增长速度要快得多。
指数爆炸
演示
图像分析
x/天 方案一 方案二 方案三
y/元 累计/元 y/元 累计/元 y/元 累计/元
1 40 10 0.4
2 40 20 0.8
3 40 30 1.6
4 40 40 3.2
5 40 50 6.4
6 40 60 12.8
7 40 70 25.6
8 40 80 51.2
9 40 90 102.4
10 40 100 204.8
11 40 110 409.6
12 40 120 819.2
40
80
0.4
30
10
1.2
120
60
2.8
160
100
6
200
150
12.4
240
210
25.2
280
280
50.8
320
360
102
360
450
204.4
400
550
409.2
440
660
818.8
x/天 方案一 方案二 方案三
y/元 累计/元 y/元 累计/元 y/元 累计/元
1 40 40 10 10 0.4 0.4
2 40 80 20 30 0.8 1.2
3 40 120 30 60 1.6 2.8
4 40 160 40 100 3.2 6
5 40 200 50 150 6.4 12.4
6 40 240 60 210 12.8 25.2
7 40 280 70 280 25.6 50.8
8 40 320 80 360 51.2 102
9 40 360 90 450 102.4 204.4
10 40 400 100 550 204.8 409.2
11 40 440 110 660 409.6 818.8
12 40 480 120 780 819.2 1638
投资1~6天,应选择方案一;
投资7天,应选择方案一或二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
结
论
常数函数 递增一次函数 递增指数型函数
几种常见函数的增长情况:
保持不变
直线上升
匀速增长
急剧增长
指数爆炸
没有增长
不同的函数增长模型,增长变化存在很大的差异!
例题的启示1
用函数模型解决实际问题的步骤:
实际问题
读懂问题
抽象概括
函数问题
演算
推理
函数问题的解
还原说明
实际问题的解
例题的启示2
例2:经过科学的选择和不懈的努力,合理投资给你带来了丰厚的收益,经过几年努力,现在你拥有了自己的公司,为了能达到1000万元利润的目标,你的助手为你制定一个激励销售部门的奖励方案。
在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,奖金总数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:
y =0.25x, y =1.002x,y =log7x +1
哪个模型能符合公司的要求?
依据?
范例讲解
(1)确定符合公司奖励方案的条件
(2)先确定奖金总数不超过5万的模型:
借助计算机通过函数图像直观的观察
分析步骤:
值域问题
分别做出函数
的图象.
绘图
初步结论: 符合要求。
(2)计算按模型 奖励时,奖金是
否不超过利润的25%
即:对 , 是否成立?
函数思想
令
作出函数 的图象:
范例讲解
3/12/2023
绘图
由图象可知它是递减的,因此
即
说明按模型 奖励,奖金不会
超过利润的25%。
综上所述,模型 确实能符合
公司要求。
范例讲解
这个奖励方案实施以后,立刻调动了员工的积极性,企业发展蒸蒸日上,但随着时间的推移,又出现了新的问题.....
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
对数增长模型:平缓增长,越来越慢
思考:
你能否为公司制定一个更好奖励模型?
2.分析函数模型的方法:
课堂小结
?
解析法
列表法
图象法
1.不同函数模型的增长特点:
直线上升 指数爆炸 对数增长
3.数学思想:
匀速递增
急剧增长
缓慢增长
一次函数 指数函数 对数函数
数形结合, 函数思想(不等式的问题转化为函数问题),建模思想
课外作业
1.材料一:借助网络收集相关的信息,了解水葫芦“疯长”的现状、原因及危害。
2.材料二:
“今人有五子不为多,子又有五子,父未死而有二十五孙。 是以民众而财寡,事力劳而供养薄”
--------韩非子
感受我国为什么要进行计划生育,撰写一个研究性学习报告?
实际问题万万千,
增长模型千千万,
数据图形细细看,
感 悟
人生高峰节节攀,
选择
爆炸
直观
拼搏
数学模型来刻画.
唯有指数最震撼.
数形结合是思想.
无限风光展未来.
天空的幸福是披一身蓝
大地的幸福是披一身绿
老师的幸福是认识了你们
愿同学们的幸福指数像指数函数一样
无穷递增!
谢谢大家!
函数模型及解决实际问题
(澳大利亚兔子数“爆炸”)
1859年,一位叫托马斯·奥斯汀英格兰农场主从欧洲带了十几只兔子到澳洲,由于这位农场主非常爱好狩猎,于是将兔子放养到其领地附近,由于澳洲有茂盛的牧草,而且没有兔子的天敌,兔子数量不断增加,短短几十年时间,兔子们占领了整个澳大利亚,数量达到75亿只.可爱的兔子变得可恶起来,75亿只兔子吃掉了大量的牧草,草原的载畜量大大降低,而牛羊是澳大利亚的主要牲口.这使澳大利亚头痛不已,他们采用各种方法消灭这些兔子,但是效果都不好,直至二十世纪五十年代,科学家采用载液瘤病毒杀死了百分之九十的野兔,澳大利亚人才算松了一口气.
(澳大利亚兔子数“爆炸”)
指数增长
一般而言,在理想条件(食物或养料充足,空间条件充裕,气候适宜,没有敌害等)下,种群在一定时期内的增长大致符合指数型“J”型曲线;在有限环境(空间有限,食物有限,有捕食者存在等)中,种群增长到一定程度后增长缓慢或不增长,曲线呈逻辑斯蒂增长“S”型.
这启发我们描述增长趋势就要恰当选取函数模型。
(线性函数、指数函数和对数函数模型)
生活中几类不同增长的函数模型
第一课时
先定一个能达到的小目标,比方说我先挣它一个亿!
例1:假设你有一笔资金用于投资,现有三种投资方案
供你选择,这三种方案的回报如下:
方案一:每天回报40元;
方案二:第一天回报10元,以后每天比前一天多回报10元;
方案三:第一天回报0.4元,以后每天的回报比前一天翻一番。
你会选择哪种投资方案呢?
分析:
①依据什么标准来选择投资方案
②分析数量关系,归纳概括相应的函数模型,建立函数关系.
回报量
每日回报
累计回报
建立日回报金额与投资天数的函数关系
投资天数
40
40
40
40
40
10
10+10
=10×2
10+10+10
=10×3
10+10+10+10
=10×4
10+10+10+10+10
=10×5
0.4
0.4×2
0.4×2×2
=0.4×22
0.4×2×2×2
=0.4×23
0.4×2×2×2×2
=0.4×24
方案一
方案二
方案三
1
2
3
4
5
则方案一可以用函数________________进行描述;
方案二可以用函数__________________描述;
方案三可以用______________________描述。
解:设第x天的回报是y元,
y=40 (x∈N*)
y=10x (x∈N*)
y=0.4×2x-1 (x∈N*)
常数函数
一次函数
指数型函数
增长情况?
数据表格 图像
我们用表格来分析三种方案每日所得回报的增长情况:
x/天
方案一
方案二
方案三
y/元
y/元
y/元
增加量
增加量
增加量
1
2
3
40
40
40
0
0
10
20
30
10
10
0.4
0.8
1.6
0.4
0.8
4
5
6
7
8
…
30
…
40
40
40
40
40
40
0
…
0
0
0
0
0
…
40
50
60
70
80
300
…
10
10
10
10
10
10
…
3.2
6.4
12.8
25.6
51.2
…
1.6
3.2
6.4
12.8
25.6
根据表格中的数据变化,三种函数的增长是存在很大差异的。
y=40 (x∈N*)
y=10x (x∈N*)
y=0.4×2x-1 (x∈N*)
214748364.8
107374182.4
o
x
y
20
40
60
80
100
120
140
4
2
6
8
10
12
当自变量较大时,底数为2的指数函数模型比线性函数模型增长速度要快得多。
指数爆炸
演示
图像分析
x/天 方案一 方案二 方案三
y/元 累计/元 y/元 累计/元 y/元 累计/元
1 40 10 0.4
2 40 20 0.8
3 40 30 1.6
4 40 40 3.2
5 40 50 6.4
6 40 60 12.8
7 40 70 25.6
8 40 80 51.2
9 40 90 102.4
10 40 100 204.8
11 40 110 409.6
12 40 120 819.2
40
80
0.4
30
10
1.2
120
60
2.8
160
100
6
200
150
12.4
240
210
25.2
280
280
50.8
320
360
102
360
450
204.4
400
550
409.2
440
660
818.8
x/天 方案一 方案二 方案三
y/元 累计/元 y/元 累计/元 y/元 累计/元
1 40 40 10 10 0.4 0.4
2 40 80 20 30 0.8 1.2
3 40 120 30 60 1.6 2.8
4 40 160 40 100 3.2 6
5 40 200 50 150 6.4 12.4
6 40 240 60 210 12.8 25.2
7 40 280 70 280 25.6 50.8
8 40 320 80 360 51.2 102
9 40 360 90 450 102.4 204.4
10 40 400 100 550 204.8 409.2
11 40 440 110 660 409.6 818.8
12 40 480 120 780 819.2 1638
投资1~6天,应选择方案一;
投资7天,应选择方案一或二;
投资8~10天,应选择方案二;
投资11天(含11天)以上,应选择方案三。
结
论
常数函数 递增一次函数 递增指数型函数
几种常见函数的增长情况:
保持不变
直线上升
匀速增长
急剧增长
指数爆炸
没有增长
不同的函数增长模型,增长变化存在很大的差异!
例题的启示1
用函数模型解决实际问题的步骤:
实际问题
读懂问题
抽象概括
函数问题
演算
推理
函数问题的解
还原说明
实际问题的解
例题的启示2
例2:经过科学的选择和不懈的努力,合理投资给你带来了丰厚的收益,经过几年努力,现在你拥有了自己的公司,为了能达到1000万元利润的目标,你的助手为你制定一个激励销售部门的奖励方案。
在销售利润达到10万元时,按销售利润进行奖励,且奖金y(单位:万元)随销售利润x(单位:万元)的增加而增加,奖金总数不超过5万元,同时奖金不超过利润的25%。现有三个奖励模型:
y =0.25x, y =1.002x,y =log7x +1
哪个模型能符合公司的要求?
依据?
范例讲解
(1)确定符合公司奖励方案的条件
(2)先确定奖金总数不超过5万的模型:
借助计算机通过函数图像直观的观察
分析步骤:
值域问题
分别做出函数
的图象.
绘图
初步结论: 符合要求。
(2)计算按模型 奖励时,奖金是
否不超过利润的25%
即:对 , 是否成立?
函数思想
令
作出函数 的图象:
范例讲解
3/12/2023
绘图
由图象可知它是递减的,因此
即
说明按模型 奖励,奖金不会
超过利润的25%。
综上所述,模型 确实能符合
公司要求。
范例讲解
这个奖励方案实施以后,立刻调动了员工的积极性,企业发展蒸蒸日上,但随着时间的推移,又出现了新的问题.....
200
400
600
800
1000
2
3
4
5
6
7
8
1
0
对数增长模型:平缓增长,越来越慢
思考:
你能否为公司制定一个更好奖励模型?
2.分析函数模型的方法:
课堂小结
?
解析法
列表法
图象法
1.不同函数模型的增长特点:
直线上升 指数爆炸 对数增长
3.数学思想:
匀速递增
急剧增长
缓慢增长
一次函数 指数函数 对数函数
数形结合, 函数思想(不等式的问题转化为函数问题),建模思想
课外作业
1.材料一:借助网络收集相关的信息,了解水葫芦“疯长”的现状、原因及危害。
2.材料二:
“今人有五子不为多,子又有五子,父未死而有二十五孙。 是以民众而财寡,事力劳而供养薄”
--------韩非子
感受我国为什么要进行计划生育,撰写一个研究性学习报告?
实际问题万万千,
增长模型千千万,
数据图形细细看,
感 悟
人生高峰节节攀,
选择
爆炸
直观
拼搏
数学模型来刻画.
唯有指数最震撼.
数形结合是思想.
无限风光展未来.
天空的幸福是披一身蓝
大地的幸福是披一身绿
老师的幸福是认识了你们
愿同学们的幸福指数像指数函数一样
无穷递增!
谢谢大家!
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
