2022-2023学年北师大版八年级数学下册 1.1等腰三角形课后强化(无答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学下册 1.1等腰三角形课后强化(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 294.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 09:55:09 | ||
图片预览

文档简介
1.1等腰三角形课后强化
一、单选题(共 8 小题)
1、“三等分角”大约是在公元前五世纪由古希腊人提出来的借助如图①所示的“三等分角仪”能三等分任意一角.如图②,这个“三等分角仪”由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,点C固定,点D,E可在槽中滑动,.若,则的度数是( )
A.24° B.27° C.30° D.33°
2、如图,四边形ABCD是正方形,M、N分别为边AB、AD的中点,点P在正方形的边上(包括顶点),且△MNP是等腰三角形,则符合条件的点P的个数有( )
A.1个 B.2个 C.3个 D.4个
3、如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )
A.35° B.40° C.45° D.50°
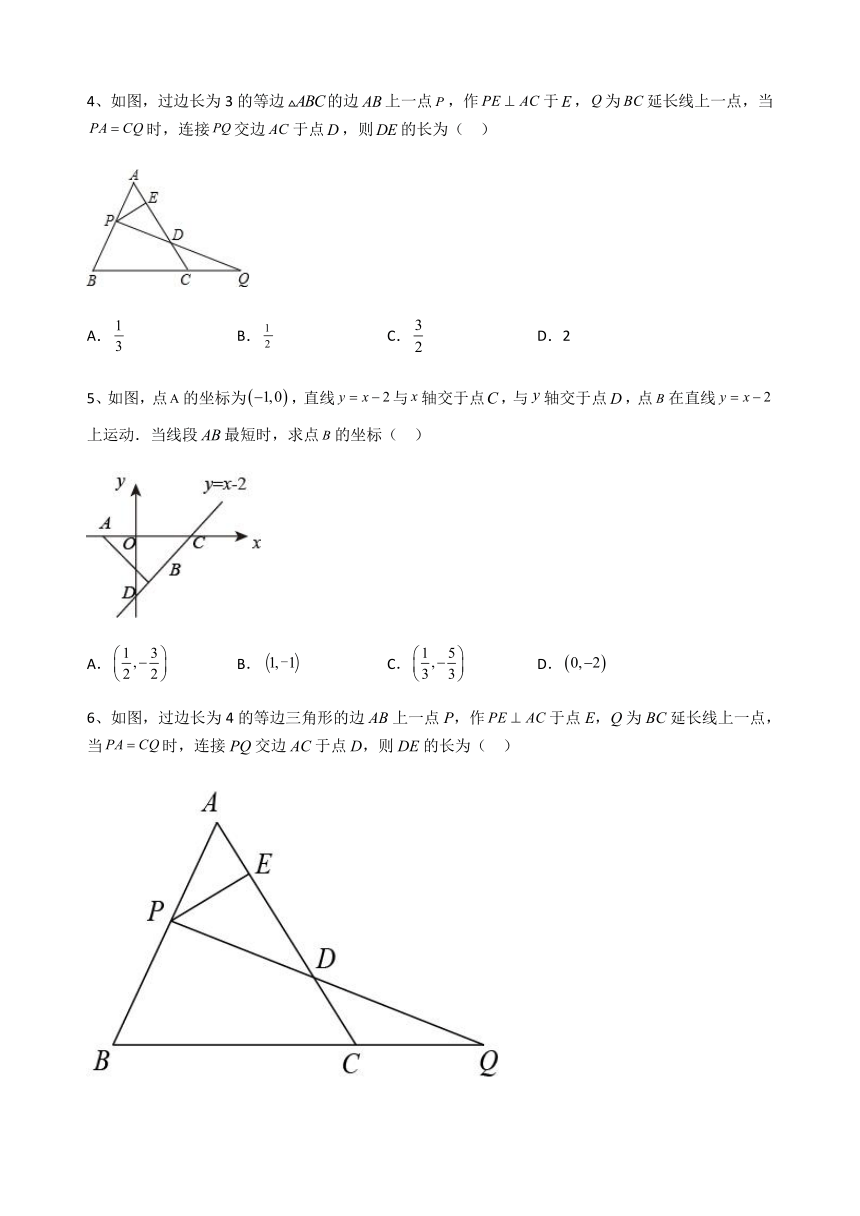
4、如图,过边长为3的等边的边上一点,作于,为延长线上一点,当时,连接交边于点,则的长为( )
A. B. C. D.2
5、如图,点的坐标为,直线与轴交于点,与轴交于点,点在直线上运动.当线段最短时,求点的坐标( )
A. B. C. D.
6、如图,过边长为4的等边三角形的边AB上一点P,作于点E,Q为BC延长线上一点,当时,连接PQ交边AC于点D,则DE的长为( )
A.2 B.3 C.4 D.
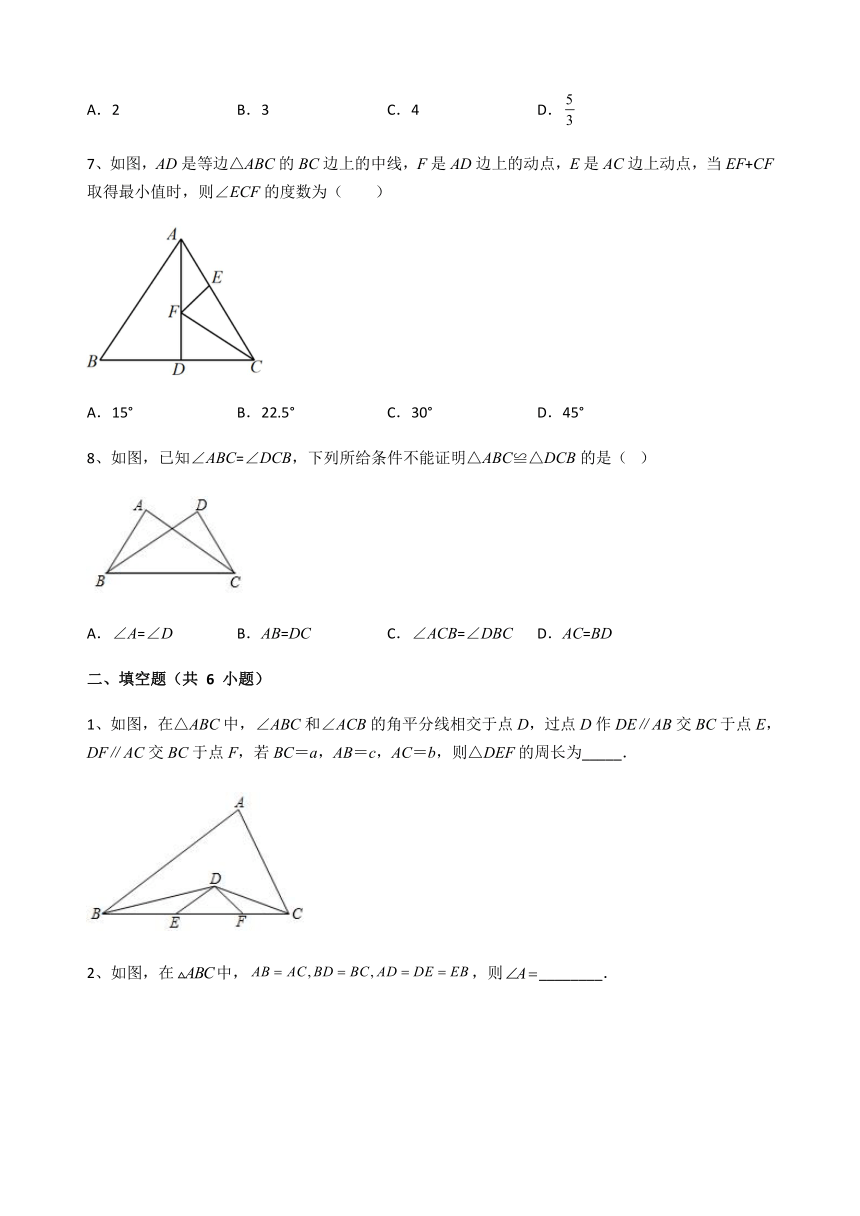
7、如图,AD是等边△ABC的BC边上的中线,F是AD边上的动点,E是AC边上动点,当EF+CF取得最小值时,则∠ECF的度数为( )
A.15° B.22.5° C.30° D.45°
8、如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
二、填空题(共 6 小题)
1、如图,在△ABC中,∠ABC和∠ACB的角平分线相交于点D,过点D作DE∥AB交BC于点E,DF∥AC交BC于点F,若BC=a,AB=c,AC=b,则△DEF的周长为_____.
2、如图,在中,,则________.
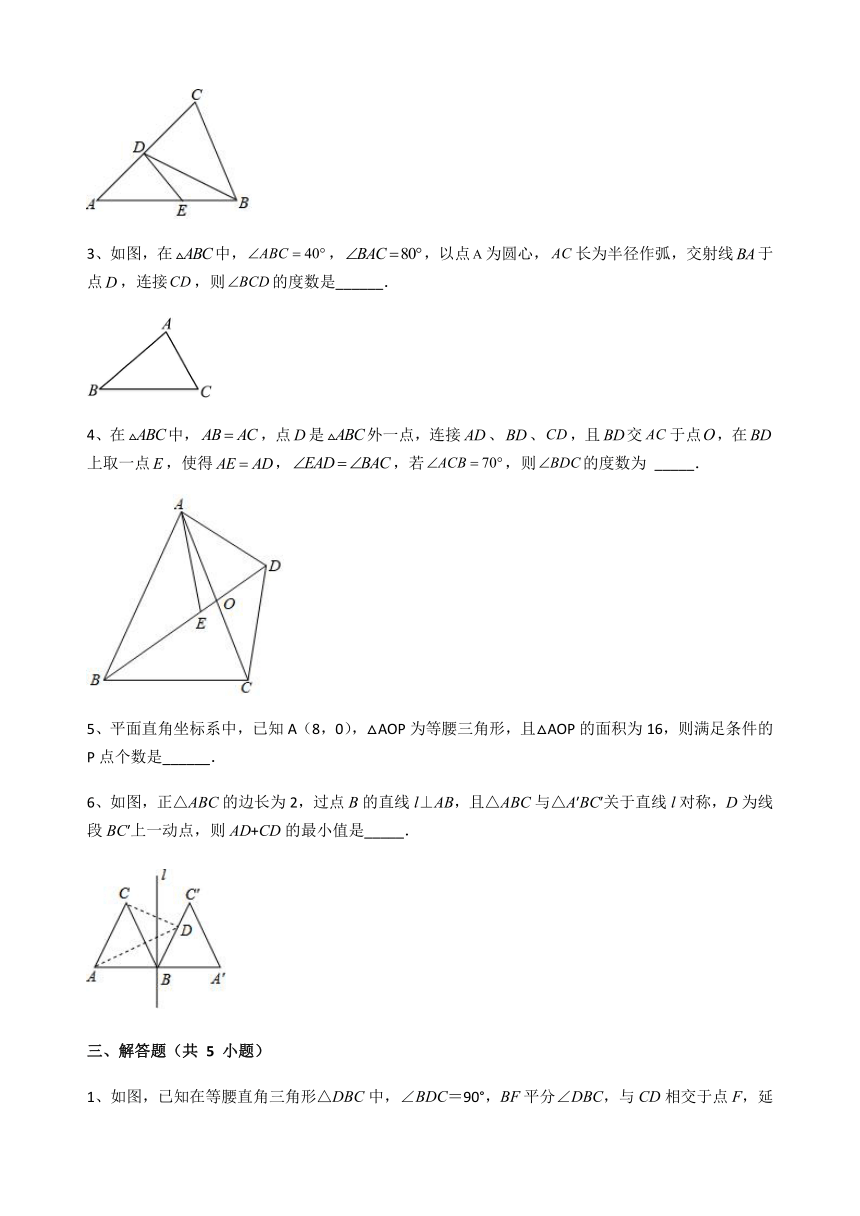
3、如图,在中,,,以点为圆心,长为半径作弧,交射线于点,连接,则的度数是______.
4、在中,,点是外一点,连接、、,且交于点,在上取一点,使得,,若,则的度数为 _____.
5、平面直角坐标系中,已知A(8,0),△AOP为等腰三角形,且△AOP的面积为16,则满足条件的P点个数是______.
6、如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是_____.
三、解答题(共 5 小题)
1、如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E.
(1)求证:△FBD≌△ACD;
(2)求证:△ABC是等腰三角形;
(3)求证:CEBF.
2、如图,已知等边中,点D、E、F分别为边、、的中点,M为直线上一动点,为等边三角形(点M的位置改变时,也随之整体移动).
(1)如图1,当点M在点B左侧时,请你连结,并判断与有怎样的数量关系?点F是否在直线上?请写出结论,并说明理由;
(2)如图2,当点M在上时,其它条件不变,(1)的结论中与的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
(3)如图3,若点M在点C右侧时,请你判断(1)的结论中与的数量关系是否仍然成立?若成立,请直接写出结论:若不成立,请说明理由.
3、如图,在中,,D为延长线上一点,且交于点F.
(1)求证:是等腰三角形,
(2)若,F为中点,求的长.
4、如图1,在平面直角坐标中,点,,,其中,点为线段上任意一点,连接,于,于.
(1)求证:;
(2)当时,若点,请你在图1中连接,交于点.求证:;
(3)若将“点为线段上任意一点”,改为“点为线段延长线上任意一点”,其他条件不变,连接,,垂足为,交轴于点,交轴于点,请在图2中补全图形,求点的坐标(用含的代数式表示).
5、如图, 在下列网格中, 每个小正方形的边长均为一个单位, 小正方形的顶点称为网格的格点.
(1) 图1为8×6网格, 点A,点B在格点上,在网格中画出以一个以AB为一边, 点C在格点上,面积为9的等腰ACB, 此时∠ABC= .
(2)图2为5×3网格,点A,点B在格点上,在网格中找出所有的点C,使得 ABC为等腰三角形,点C在格点上.(在找到的点上标上点C1,C2,C3… )
一、单选题(共 8 小题)
1、“三等分角”大约是在公元前五世纪由古希腊人提出来的借助如图①所示的“三等分角仪”能三等分任意一角.如图②,这个“三等分角仪”由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,点C固定,点D,E可在槽中滑动,.若,则的度数是( )
A.24° B.27° C.30° D.33°
2、如图,四边形ABCD是正方形,M、N分别为边AB、AD的中点,点P在正方形的边上(包括顶点),且△MNP是等腰三角形,则符合条件的点P的个数有( )
A.1个 B.2个 C.3个 D.4个
3、如图, BD 是△ABC 的角平分线, AE⊥ BD ,垂足为 F ,若∠ABC=35°,∠ C=50°,则∠CDE 的度数为( )
A.35° B.40° C.45° D.50°
4、如图,过边长为3的等边的边上一点,作于,为延长线上一点,当时,连接交边于点,则的长为( )
A. B. C. D.2
5、如图,点的坐标为,直线与轴交于点,与轴交于点,点在直线上运动.当线段最短时,求点的坐标( )
A. B. C. D.
6、如图,过边长为4的等边三角形的边AB上一点P,作于点E,Q为BC延长线上一点,当时,连接PQ交边AC于点D,则DE的长为( )
A.2 B.3 C.4 D.
7、如图,AD是等边△ABC的BC边上的中线,F是AD边上的动点,E是AC边上动点,当EF+CF取得最小值时,则∠ECF的度数为( )
A.15° B.22.5° C.30° D.45°
8、如图,已知∠ABC=∠DCB,下列所给条件不能证明△ABC≌△DCB的是( )
A.∠A=∠D B.AB=DC C.∠ACB=∠DBC D.AC=BD
二、填空题(共 6 小题)
1、如图,在△ABC中,∠ABC和∠ACB的角平分线相交于点D,过点D作DE∥AB交BC于点E,DF∥AC交BC于点F,若BC=a,AB=c,AC=b,则△DEF的周长为_____.
2、如图,在中,,则________.
3、如图,在中,,,以点为圆心,长为半径作弧,交射线于点,连接,则的度数是______.
4、在中,,点是外一点,连接、、,且交于点,在上取一点,使得,,若,则的度数为 _____.
5、平面直角坐标系中,已知A(8,0),△AOP为等腰三角形,且△AOP的面积为16,则满足条件的P点个数是______.
6、如图,正△ABC的边长为2,过点B的直线l⊥AB,且△ABC与△A′BC′关于直线l对称,D为线段BC′上一动点,则AD+CD的最小值是_____.
三、解答题(共 5 小题)
1、如图,已知在等腰直角三角形△DBC中,∠BDC=90°,BF平分∠DBC,与CD相交于点F,延长BD到A,使DA=DF,延长BF交AC于E.
(1)求证:△FBD≌△ACD;
(2)求证:△ABC是等腰三角形;
(3)求证:CEBF.
2、如图,已知等边中,点D、E、F分别为边、、的中点,M为直线上一动点,为等边三角形(点M的位置改变时,也随之整体移动).
(1)如图1,当点M在点B左侧时,请你连结,并判断与有怎样的数量关系?点F是否在直线上?请写出结论,并说明理由;
(2)如图2,当点M在上时,其它条件不变,(1)的结论中与的数量关系是否仍然成立?若成立,请利用图2证明;若不成立,请说明理由;
(3)如图3,若点M在点C右侧时,请你判断(1)的结论中与的数量关系是否仍然成立?若成立,请直接写出结论:若不成立,请说明理由.
3、如图,在中,,D为延长线上一点,且交于点F.
(1)求证:是等腰三角形,
(2)若,F为中点,求的长.
4、如图1,在平面直角坐标中,点,,,其中,点为线段上任意一点,连接,于,于.
(1)求证:;
(2)当时,若点,请你在图1中连接,交于点.求证:;
(3)若将“点为线段上任意一点”,改为“点为线段延长线上任意一点”,其他条件不变,连接,,垂足为,交轴于点,交轴于点,请在图2中补全图形,求点的坐标(用含的代数式表示).
5、如图, 在下列网格中, 每个小正方形的边长均为一个单位, 小正方形的顶点称为网格的格点.
(1) 图1为8×6网格, 点A,点B在格点上,在网格中画出以一个以AB为一边, 点C在格点上,面积为9的等腰ACB, 此时∠ABC= .
(2)图2为5×3网格,点A,点B在格点上,在网格中找出所有的点C,使得 ABC为等腰三角形,点C在格点上.(在找到的点上标上点C1,C2,C3… )
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
