物理人教版(2019)必修第二册6.4 生活中的圆周运动(共53张ppt)
文档属性
| 名称 | 物理人教版(2019)必修第二册6.4 生活中的圆周运动(共53张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 31.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-13 16:19:51 | ||
图片预览










文档简介
(共53张PPT)
第
节
4
生活中的圆周运动
高中物理 必修第二册
第六章
提供物体做
圆周运动的力
物体做圆周运动所需的力
物体作圆周运动的条件
从“供” “需”两方面研究生活中做圆周运动的物体
由物体受力情况决定
由物体的运动情况决定
F
=
“供需”平衡 物体做圆周运动
本节课
牛顿第二定律F=ma的应用
知识回顾
提供量
需求量
一、火车转弯
火车为什么会发生脱轨事故呢?
一、火车转弯
火车转弯是什么力提供向心力?
铁轨
踏面
轮缘
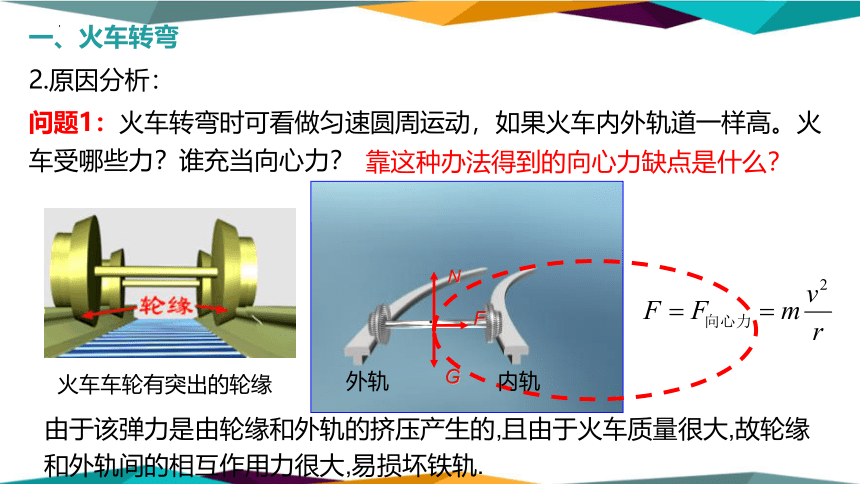
1.车轮构造:
一、火车转弯
G
N
.
F
火车车轮有突出的轮缘
外轨
内轨
问题1:火车转弯时可看做匀速圆周运动,如果火车内外轨道一样高。火车受哪些力?谁充当向心力?
靠这种办法得到的向心力缺点是什么?
2.原因分析:
由于该弹力是由轮缘和外轨的挤压产生的,且由于火车质量很大,故轮缘和外轨间的相互作用力很大,易损坏铁轨.
一、火车转弯
问题2:如何设计可以克服上述缺点?
问题3:若不受侧向轨道的弹力,谁充当向心力
一、火车转弯
质量为m的火车转弯时,做匀速圆周运动的轨道半径为r,轨道的倾角为θ,求火车速度多大时对轨道无侧向压力。
火车转弯规定临界速度:
G
Fn
N
θ
θ
r
一、火车转弯
高速公路转弯处和场地自行车比赛的赛道,路面往往有一定的斜度。说说这样设计的原因?
路面是倾斜的
外高内低
一段铁路转弯处,内外轨高度差为h=10 cm,弯道半径为r=625 m,轨距l=1 435 mm,求这段弯道的设计速度v0是多大。讨论当火车速度大于或小于v0时内外轨所受的侧压力(g取10 m/s2)。
一、火车转弯
[答案] 75 km/h 讨论见解析
一、火车转弯
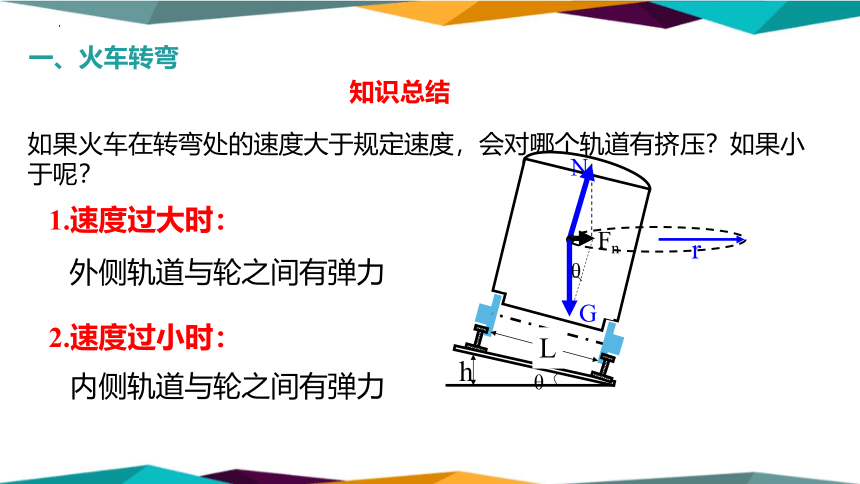
如果火车在转弯处的速度大于规定速度,会对哪个轨道有挤压?如果小于呢?
1.速度过大时:
2.速度过小时:
外侧轨道与轮之间有弹力
内侧轨道与轮之间有弹力
G
Fn
N
h
L
θ
θ
r
知识总结
C
2.(多选)公路急转弯处通常是交通事故多发地带。如图所示,某公路急转弯处是一圆弧,当汽车行驶的速率为v0时,汽车恰好没有向公路内外两侧滑动的趋势,则在该弯道处( )
A.路面外侧高、内侧低
B.车速只要低于v0,车辆便会向内侧滑动
C.车速虽然高于v0,但只要不超出某一最高限度,车辆便不会向外侧滑动
D.当路面结冰时,与未结冰时相比,v0的值变小
AC
赛车为什么会腾空而起?
二、汽车过拱形桥
二、汽车过拱形桥
为何这三种路面容易爆胎
波浪形公路
带横向水沟的公路
二、汽车过拱形桥
二、汽车过拱形桥
拱形桥
(凸形桥)
凹形桥
水平桥
二、汽车过拱形桥
问题1:汽车静止在桥上与通过平桥时,受力怎样?
F压=FN=mg
二、汽车过拱形桥
问题2:汽车过拱形桥时,在最高点时,车对凸桥的压力又怎样?
mg
FN
v2
R
mg-FN=m
v2
R
FN =mg-m
v2
R
F压=FN =mg-m
汽车对桥的压力小于其所受重力,即处于失重
FN <mg
二、汽车过拱形桥
v2
R
mg=m
当 FN = 0 时,汽车脱离桥面,做平抛运动,汽车及其中的物体处于完全失重状态。
FN=0 时,汽车的速度为多大?
v2
R
FN =mg-m
问题3:汽车过拱形桥时,运动速度变大,车对凸桥的压力如何变化?
mg
FN
临界速度
二、汽车过拱形桥
问题4:汽车过凹形桥时,在最低点时,车对凹形桥的压力又怎样?
FN
mg
v2
R
FN =mg + m
v2
R
F压=FN =mg + m
v2
R
FN-mg=m
汽车对桥的压力大于其所受重力,即处于超重
若汽车通过凹桥的速度增大,会出现什么情况?
FN >mg
二、汽车过拱形桥
汽车对桥面的压力 超重失重状态
最高点
最低点
小结:
失重
超重
如图所示,质量m=2.0×104 kg的汽车以不变的速率先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20 m。如果桥面承受的压力不得超过3.0×105 N,则:
(1)汽车允许的最大速率是多少?
(2)若以所求速度行驶,汽车对桥面的最小压力是多少?(g取10 m/s2)
二、汽车过拱形桥
[答案] (1)10 m/s (2)1.0×105 N
二、汽车过拱形桥
B
二、汽车过拱形桥
4.公路在通过小型水库的泄洪闸的下游时常常要修建凹形路面,也叫“过水路面”。如图所示,汽车通过凹形路面的最低点时( )
A.车对路面的压力等于汽车的重力
B.车对路面的压力小于路面对汽车的支持力
C.汽车所需的向心力就是地面对车的支持力
D.为了防止爆胎,车应低速驶过
D
二、汽车过拱形桥
二、汽车过拱形桥
三、航天器中的失重现象
地球可以看做一个巨大的拱形桥,桥面的半径就是地球的半径.会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是零?这时驾驶员与座椅之间的压力是多少?……
地球可以看作一个巨大的拱型桥,其半径就是地球半径R= 6400km,若汽车不断加速,则地面对它的支持力就会变小,汽车速度多大时,支持力会变成零FN=0?
由
得
此时司机处于完全失重状态。
三、航天器中的失重现象
问题2、航天器在轨道正常运行(绕地球做匀速圆周运动)时,航天员处在超重还是失重状态?
FN
mg
a
FN-mg =ma
FN>mg
问题1、航天器在发射升空(加速上升)时,航天员处在超重还是失重状态?
四、离心运动
问题1.分析下面视频中运动产生的原因(条件)?
四、离心运动
汽车在转弯的时候运动情况分析
O
F静
v
向心力是由车轮与路面的静摩擦力提供的.如果转弯时速度过大,所需向心力Fn大于最大静摩擦力Fmax (Fmax不足以提供向心力),汽车将做远离圆心的运动而造成交通事故.因此,在公路弯道处,车辆行驶不允许超过规定的速度.
当 时,汽车做离心运动
Fmax<m
v2
r
四、离心运动
F合<mω2r ,
1、定义:做匀速圆周运动的物体,在所受合力突然消失,或者不足以提供圆周运动所需的向心力时,做逐渐远离圆心的运动,这种运动叫做离心运动.
O
F合 = mω2r,
F 合= 0 ,
物体沿切线方向飞出远离圆心
物体做匀速圆周运动
物体做逐渐远离圆心的运动
2.条件:
0 ≤F合<mω2r
F =
F <
F >
匀速圆周运动
离心运动
向心运动
四、离心运动
问题2.离心运动在生活中应用在哪些地方?
离心抛掷
离心脱水
离心分离
离心甩干
如图所示是摩托车比赛转弯时的情形。转弯处路面常是外高内低,摩托车转弯有一个最大安全速度,若超过此速度,摩托车将发生滑动。关于摩托车向外滑动的问题,下列论述正确的是( )
A.摩托车一直受到沿半径方向向外的离心力作用
B.摩托车所受外力的合力小于所需的向心力
C.摩托车将沿其线速度的方向沿直线滑去
D.摩托车将沿其半径方向沿直线滑去
B
四、离心运动
5.在冬奥会短道速滑项目中,运动员绕周长仅111米的短道竞赛。比赛过程中运动员在通过弯道时如果不能很好地控制速度,将发生侧滑而甩离正常比赛路线。如图所示,圆弧虚线Ob代表弯道,即正常运动路线,Oa为运动员在O点时的速度方向(研究时可将运动员看作质点)。下列论述正确的是( )
A.发生侧滑是因为运动员受到的合力方向背离圆心
B.发生侧滑是因为运动员受到的合力大于所需要的向心力
C.若在O点发生侧滑,则滑动的方向在Oa左侧
D.若在O点发生侧滑,则滑动的方向在Oa右侧与Ob之间
D
四、离心运动
6.(多选)如图甲所示,在光滑水平转台上放一木块A,用细绳的一端系住木块A,另一端穿过转台中心的光滑小孔O悬挂另一木块B。当转台以角速度ω匀速转动时,A恰能随转台一起做匀速圆周运动,图乙为其俯视图,则( )
四、离心运动
A.当转台的角速度变为1.5ω时,木块A将沿图乙中的a方向运动
B.当转台的角速度变为1.5ω时,木块A将沿图乙中的b方向运动
C.当转台的角速度变为0.5ω时,木块A将沿图乙中的b方向运动
D.当转台的角速度变为0.5ω时,木块A将沿图乙中的c方向运动
答案:BD
四、离心运动
五、竖直面内圆周运动的临界问题
问题1.现在你能不能解释水流星为什么杯子倒过来的时候水没有流出来?
五、竖直面内圆周运动的临界问题
N=0时临界情况水恰好不掉出,
临界速度
当 时,杯里的水做向心运动,没到最高点就会洒下来。
是“水流星”表演成功的关键.
G
N
在“水流星”表演中,杯子在竖直平面做圆周运动。在最高点时,杯口朝下,但杯中水却不会流下来,为什么?
1.水流星之谜
五、竖直面内圆周运动的临界问题
mg
T
v
o
问题2:在最高点时,何时杆表现为拉力?何时杆表现为支持力?试求其临界速度。
杆球模型:
最高点:
拉力
支持力
临界速度:
当v当v>v0,杆对球有向下的拉力;
问题1:最高点的最小速度是多少
最小速度v=0,此时mg=N
N
mg
v
o
五、竖直面内圆周运动的临界问题
总结:竖直平面内圆周运动的临界问题
课堂小结
1.讨论向心力的来源
2.外轨高于内轨时重力与支持力的合力是使火车转弯的向心力
3.讨论:为什么转弯处的半径和火车运行速度有条件限制
生活中的圆周运动
铁路的弯道
1.离心现象的分析与讨论.
2.离心运动的应用和防止.
汽车过拱形桥和凹形桥
1.思考:汽车过拱形桥时,对桥面的压力
与重力谁大
2.圆周运动中的超重、失重情况.
航天器中的失重现象
离心运动
竖直面内圆周运动的临界问题
1.轻绳模型
2.轻杆模型
课堂练习
1.(火车转弯问题)(多选)铁路转弯处的弯道半径r是根据地形决定的。弯道处要求外轨比内轨高,其内外轨高度差h的设计不仅与r有关,还与火车在弯道上的行驶速率v有关。下列说法正确的是( )
A.v一定时,r越小则要求h越大
B.v一定时,r越大则要求h越大
C.r一定时,v越小则要求h越大
D.r一定时,v越大则要求h越大
答案:AD
课堂练习
越小,故A正确,B错误。当r一定时,v越大,h越大,故C错误,D正确。
课堂练习
2.(离心现象)下列事例利用了离心现象的是( )
答案:D
课堂练习
解析:自行车赛道倾斜,应用了支持力与重力的合力提供向心力,防止产生离心运动,故A错误。因为Fn=m ,所以速度越快所需的向心力就越大,汽车转弯时要限制速度,来减小汽车所需的向心力,防止离心运动,故B错误。汽车上坡前加速,与离心运动无关,故C错误。拖把利用旋转脱水,就是利用了离心运动,故D正确。
课堂练习
3.(失重现象的分析)(多选)宇航员在围绕地球做匀速圆周运动的空间站中处于完全失重状态,下列说法正确的是( )
A.宇航员仍受重力的作用
B.宇航员受力平衡
C.宇航员所受重力等于所需的向心力
D.宇航员不受重力的作用
答案:AC
解析:围绕地球做匀速圆周运动的空间站中的宇航员,所受重力全部提供其做圆周运动的向心力,处于完全失重状态,并非宇航员不受重力作用,A、C正确,B、D错误。
课堂练习
4.(竖直平面内的圆周运动)一轻绳系着装有水的水桶,在竖直平面内做圆周运动,水的质量m=0.5 kg,绳长l=60 cm,g取9.8 m/s2。
(1)求在最高点时水不会流出的桶的
最小速率。
(2)水在最高点的速率v=3 m/s时,
求水对桶底的压力。
答案:(1)2.42 m/s
(2)2.6 N,方向竖直向上
课堂练习
解析:(1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水的重力恰好提供其做圆周运动所需的向心力,此时水的速率最小。设在最高点时的临界速率为v0,
(2)在最高点时,桶的速率v>v0,此时桶底对水有一向下的压力,
由牛顿第三定律可得,水对桶底的压力FN'=FN=2.6 N,方向竖直向上。
多谢欣赏!
第
节
4
生活中的圆周运动
高中物理 必修第二册
第六章
提供物体做
圆周运动的力
物体做圆周运动所需的力
物体作圆周运动的条件
从“供” “需”两方面研究生活中做圆周运动的物体
由物体受力情况决定
由物体的运动情况决定
F
=
“供需”平衡 物体做圆周运动
本节课
牛顿第二定律F=ma的应用
知识回顾
提供量
需求量
一、火车转弯
火车为什么会发生脱轨事故呢?
一、火车转弯
火车转弯是什么力提供向心力?
铁轨
踏面
轮缘
1.车轮构造:
一、火车转弯
G
N
.
F
火车车轮有突出的轮缘
外轨
内轨
问题1:火车转弯时可看做匀速圆周运动,如果火车内外轨道一样高。火车受哪些力?谁充当向心力?
靠这种办法得到的向心力缺点是什么?
2.原因分析:
由于该弹力是由轮缘和外轨的挤压产生的,且由于火车质量很大,故轮缘和外轨间的相互作用力很大,易损坏铁轨.
一、火车转弯
问题2:如何设计可以克服上述缺点?
问题3:若不受侧向轨道的弹力,谁充当向心力
一、火车转弯
质量为m的火车转弯时,做匀速圆周运动的轨道半径为r,轨道的倾角为θ,求火车速度多大时对轨道无侧向压力。
火车转弯规定临界速度:
G
Fn
N
θ
θ
r
一、火车转弯
高速公路转弯处和场地自行车比赛的赛道,路面往往有一定的斜度。说说这样设计的原因?
路面是倾斜的
外高内低
一段铁路转弯处,内外轨高度差为h=10 cm,弯道半径为r=625 m,轨距l=1 435 mm,求这段弯道的设计速度v0是多大。讨论当火车速度大于或小于v0时内外轨所受的侧压力(g取10 m/s2)。
一、火车转弯
[答案] 75 km/h 讨论见解析
一、火车转弯
如果火车在转弯处的速度大于规定速度,会对哪个轨道有挤压?如果小于呢?
1.速度过大时:
2.速度过小时:
外侧轨道与轮之间有弹力
内侧轨道与轮之间有弹力
G
Fn
N
h
L
θ
θ
r
知识总结
C
2.(多选)公路急转弯处通常是交通事故多发地带。如图所示,某公路急转弯处是一圆弧,当汽车行驶的速率为v0时,汽车恰好没有向公路内外两侧滑动的趋势,则在该弯道处( )
A.路面外侧高、内侧低
B.车速只要低于v0,车辆便会向内侧滑动
C.车速虽然高于v0,但只要不超出某一最高限度,车辆便不会向外侧滑动
D.当路面结冰时,与未结冰时相比,v0的值变小
AC
赛车为什么会腾空而起?
二、汽车过拱形桥
二、汽车过拱形桥
为何这三种路面容易爆胎
波浪形公路
带横向水沟的公路
二、汽车过拱形桥
二、汽车过拱形桥
拱形桥
(凸形桥)
凹形桥
水平桥
二、汽车过拱形桥
问题1:汽车静止在桥上与通过平桥时,受力怎样?
F压=FN=mg
二、汽车过拱形桥
问题2:汽车过拱形桥时,在最高点时,车对凸桥的压力又怎样?
mg
FN
v2
R
mg-FN=m
v2
R
FN =mg-m
v2
R
F压=FN =mg-m
汽车对桥的压力小于其所受重力,即处于失重
FN <mg
二、汽车过拱形桥
v2
R
mg=m
当 FN = 0 时,汽车脱离桥面,做平抛运动,汽车及其中的物体处于完全失重状态。
FN=0 时,汽车的速度为多大?
v2
R
FN =mg-m
问题3:汽车过拱形桥时,运动速度变大,车对凸桥的压力如何变化?
mg
FN
临界速度
二、汽车过拱形桥
问题4:汽车过凹形桥时,在最低点时,车对凹形桥的压力又怎样?
FN
mg
v2
R
FN =mg + m
v2
R
F压=FN =mg + m
v2
R
FN-mg=m
汽车对桥的压力大于其所受重力,即处于超重
若汽车通过凹桥的速度增大,会出现什么情况?
FN >mg
二、汽车过拱形桥
汽车对桥面的压力 超重失重状态
最高点
最低点
小结:
失重
超重
如图所示,质量m=2.0×104 kg的汽车以不变的速率先后驶过凹形桥面和凸形桥面,两桥面的圆弧半径均为20 m。如果桥面承受的压力不得超过3.0×105 N,则:
(1)汽车允许的最大速率是多少?
(2)若以所求速度行驶,汽车对桥面的最小压力是多少?(g取10 m/s2)
二、汽车过拱形桥
[答案] (1)10 m/s (2)1.0×105 N
二、汽车过拱形桥
B
二、汽车过拱形桥
4.公路在通过小型水库的泄洪闸的下游时常常要修建凹形路面,也叫“过水路面”。如图所示,汽车通过凹形路面的最低点时( )
A.车对路面的压力等于汽车的重力
B.车对路面的压力小于路面对汽车的支持力
C.汽车所需的向心力就是地面对车的支持力
D.为了防止爆胎,车应低速驶过
D
二、汽车过拱形桥
二、汽车过拱形桥
三、航天器中的失重现象
地球可以看做一个巨大的拱形桥,桥面的半径就是地球的半径.会不会出现这样的情况:速度大到一定程度时,地面对车的支持力是零?这时驾驶员与座椅之间的压力是多少?……
地球可以看作一个巨大的拱型桥,其半径就是地球半径R= 6400km,若汽车不断加速,则地面对它的支持力就会变小,汽车速度多大时,支持力会变成零FN=0?
由
得
此时司机处于完全失重状态。
三、航天器中的失重现象
问题2、航天器在轨道正常运行(绕地球做匀速圆周运动)时,航天员处在超重还是失重状态?
FN
mg
a
FN-mg =ma
FN>mg
问题1、航天器在发射升空(加速上升)时,航天员处在超重还是失重状态?
四、离心运动
问题1.分析下面视频中运动产生的原因(条件)?
四、离心运动
汽车在转弯的时候运动情况分析
O
F静
v
向心力是由车轮与路面的静摩擦力提供的.如果转弯时速度过大,所需向心力Fn大于最大静摩擦力Fmax (Fmax不足以提供向心力),汽车将做远离圆心的运动而造成交通事故.因此,在公路弯道处,车辆行驶不允许超过规定的速度.
当 时,汽车做离心运动
Fmax<m
v2
r
四、离心运动
F合<mω2r ,
1、定义:做匀速圆周运动的物体,在所受合力突然消失,或者不足以提供圆周运动所需的向心力时,做逐渐远离圆心的运动,这种运动叫做离心运动.
O
F合 = mω2r,
F 合= 0 ,
物体沿切线方向飞出远离圆心
物体做匀速圆周运动
物体做逐渐远离圆心的运动
2.条件:
0 ≤F合<mω2r
F =
F <
F >
匀速圆周运动
离心运动
向心运动
四、离心运动
问题2.离心运动在生活中应用在哪些地方?
离心抛掷
离心脱水
离心分离
离心甩干
如图所示是摩托车比赛转弯时的情形。转弯处路面常是外高内低,摩托车转弯有一个最大安全速度,若超过此速度,摩托车将发生滑动。关于摩托车向外滑动的问题,下列论述正确的是( )
A.摩托车一直受到沿半径方向向外的离心力作用
B.摩托车所受外力的合力小于所需的向心力
C.摩托车将沿其线速度的方向沿直线滑去
D.摩托车将沿其半径方向沿直线滑去
B
四、离心运动
5.在冬奥会短道速滑项目中,运动员绕周长仅111米的短道竞赛。比赛过程中运动员在通过弯道时如果不能很好地控制速度,将发生侧滑而甩离正常比赛路线。如图所示,圆弧虚线Ob代表弯道,即正常运动路线,Oa为运动员在O点时的速度方向(研究时可将运动员看作质点)。下列论述正确的是( )
A.发生侧滑是因为运动员受到的合力方向背离圆心
B.发生侧滑是因为运动员受到的合力大于所需要的向心力
C.若在O点发生侧滑,则滑动的方向在Oa左侧
D.若在O点发生侧滑,则滑动的方向在Oa右侧与Ob之间
D
四、离心运动
6.(多选)如图甲所示,在光滑水平转台上放一木块A,用细绳的一端系住木块A,另一端穿过转台中心的光滑小孔O悬挂另一木块B。当转台以角速度ω匀速转动时,A恰能随转台一起做匀速圆周运动,图乙为其俯视图,则( )
四、离心运动
A.当转台的角速度变为1.5ω时,木块A将沿图乙中的a方向运动
B.当转台的角速度变为1.5ω时,木块A将沿图乙中的b方向运动
C.当转台的角速度变为0.5ω时,木块A将沿图乙中的b方向运动
D.当转台的角速度变为0.5ω时,木块A将沿图乙中的c方向运动
答案:BD
四、离心运动
五、竖直面内圆周运动的临界问题
问题1.现在你能不能解释水流星为什么杯子倒过来的时候水没有流出来?
五、竖直面内圆周运动的临界问题
N=0时临界情况水恰好不掉出,
临界速度
当 时,杯里的水做向心运动,没到最高点就会洒下来。
是“水流星”表演成功的关键.
G
N
在“水流星”表演中,杯子在竖直平面做圆周运动。在最高点时,杯口朝下,但杯中水却不会流下来,为什么?
1.水流星之谜
五、竖直面内圆周运动的临界问题
mg
T
v
o
问题2:在最高点时,何时杆表现为拉力?何时杆表现为支持力?试求其临界速度。
杆球模型:
最高点:
拉力
支持力
临界速度:
当v
问题1:最高点的最小速度是多少
最小速度v=0,此时mg=N
N
mg
v
o
五、竖直面内圆周运动的临界问题
总结:竖直平面内圆周运动的临界问题
课堂小结
1.讨论向心力的来源
2.外轨高于内轨时重力与支持力的合力是使火车转弯的向心力
3.讨论:为什么转弯处的半径和火车运行速度有条件限制
生活中的圆周运动
铁路的弯道
1.离心现象的分析与讨论.
2.离心运动的应用和防止.
汽车过拱形桥和凹形桥
1.思考:汽车过拱形桥时,对桥面的压力
与重力谁大
2.圆周运动中的超重、失重情况.
航天器中的失重现象
离心运动
竖直面内圆周运动的临界问题
1.轻绳模型
2.轻杆模型
课堂练习
1.(火车转弯问题)(多选)铁路转弯处的弯道半径r是根据地形决定的。弯道处要求外轨比内轨高,其内外轨高度差h的设计不仅与r有关,还与火车在弯道上的行驶速率v有关。下列说法正确的是( )
A.v一定时,r越小则要求h越大
B.v一定时,r越大则要求h越大
C.r一定时,v越小则要求h越大
D.r一定时,v越大则要求h越大
答案:AD
课堂练习
越小,故A正确,B错误。当r一定时,v越大,h越大,故C错误,D正确。
课堂练习
2.(离心现象)下列事例利用了离心现象的是( )
答案:D
课堂练习
解析:自行车赛道倾斜,应用了支持力与重力的合力提供向心力,防止产生离心运动,故A错误。因为Fn=m ,所以速度越快所需的向心力就越大,汽车转弯时要限制速度,来减小汽车所需的向心力,防止离心运动,故B错误。汽车上坡前加速,与离心运动无关,故C错误。拖把利用旋转脱水,就是利用了离心运动,故D正确。
课堂练习
3.(失重现象的分析)(多选)宇航员在围绕地球做匀速圆周运动的空间站中处于完全失重状态,下列说法正确的是( )
A.宇航员仍受重力的作用
B.宇航员受力平衡
C.宇航员所受重力等于所需的向心力
D.宇航员不受重力的作用
答案:AC
解析:围绕地球做匀速圆周运动的空间站中的宇航员,所受重力全部提供其做圆周运动的向心力,处于完全失重状态,并非宇航员不受重力作用,A、C正确,B、D错误。
课堂练习
4.(竖直平面内的圆周运动)一轻绳系着装有水的水桶,在竖直平面内做圆周运动,水的质量m=0.5 kg,绳长l=60 cm,g取9.8 m/s2。
(1)求在最高点时水不会流出的桶的
最小速率。
(2)水在最高点的速率v=3 m/s时,
求水对桶底的压力。
答案:(1)2.42 m/s
(2)2.6 N,方向竖直向上
课堂练习
解析:(1)以水桶中的水为研究对象,在最高点恰好不流出来,说明水的重力恰好提供其做圆周运动所需的向心力,此时水的速率最小。设在最高点时的临界速率为v0,
(2)在最高点时,桶的速率v>v0,此时桶底对水有一向下的压力,
由牛顿第三定律可得,水对桶底的压力FN'=FN=2.6 N,方向竖直向上。
多谢欣赏!
