湖南省郴州市嘉禾县校际联考2022-2023学年八年级上学期期末数学试题(含解析)
文档属性
| 名称 | 湖南省郴州市嘉禾县校际联考2022-2023学年八年级上学期期末数学试题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 400.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 22:06:55 | ||
图片预览



文档简介
2022-2023学年上学期期末学业水平检测
八年级数学
一、单选题(共40分)
1. 如图,四个图标分别是剑桥大学、北京大学、浙江大学和北京理工大学的校徽的重要组成部分,其中是轴对称图形的是( )
A. B.
C. D.
2. 下列分解因式正确的是( )
A. B.=
C. D.
3. 下列计算正确的是( )
A. B.
C. D.
4. 若a+b=3,则2a2+4ab+2b2-6的值是( )
A.12 B.6 C.3 D.0
5. 暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )
A. B.
C. D.
6. 如图,人字梯中间一般会设计一 “拉杆”,以增加使用梯子时的安全性这样做的道理是( )
A.两点之间的所有连线中线段最短
B.三角形具有稳定性
C.经过两点有一条直线,并且只有一条直线拉杆
D.在连接直线外一点与直线上各点的线段中,垂线段最短
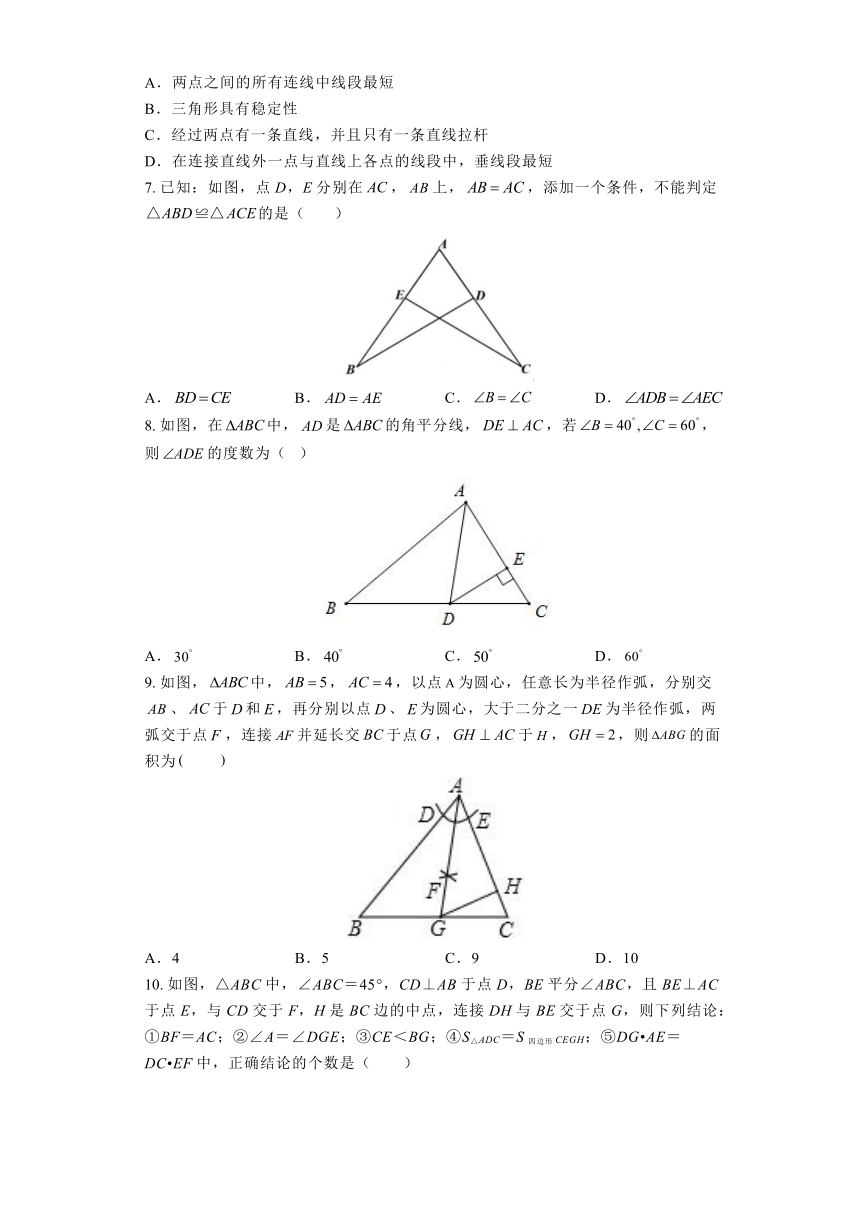
7. 已知:如图,点D,E分别在,上,,添加一个条件,不能判定的是( )
A. B. C. D.
8. 如图,在中,是的角平分线,,若,则的度数为( )
A. B. C. D.
9. 如图,中,,,以点为圆心,任意长为半径作弧,分别交、于和,再分别以点、为圆心,大于二分之一为半径作弧,两弧交于点,连接并延长交于点,于,,则的面积为
A.4 B.5 C.9 D.10
10. 如图,△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD交于F,H是BC边的中点,连接DH与BE交于点G,则下列结论:
①BF=AC;②∠A=∠DGE;③CE<BG;④S△ADC=S四边形CEGH;⑤DG AE=DC EF中,正确结论的个数是( )
A.2 B.3 C.4 D.5
二、填空题(共25分)
11. 因式分解:4+12(x-y)+9(x-y)2= .
12. 已知﹣=3,则分式的值为 .
13. ≌,,,若的周长为偶数,则 .
14. 如图,在矩形ABCD中,AB=8cm,AD=12cm,点P从点B出发,以2cm/s的速度沿BC边向点C运动,到达点C停止,同时,点Q从点C出发,以vcm/s的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v为 时,△ABP与△PCQ全等.
15. 如图,在△中,已知点分别为的中点,若△的面积为,则阴影部分的面积为
三、解答题(共55分)
16. (1)计算下列式子:(10分)
①= ;
②= .
(2) 先化简,再求值:,其中.
17. 如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.(10分)
求证:(1)∠D=∠B;
(2)AE∥CF.
18. 在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.(10分)
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
19. (1)下面是小颖同学解分式方程=1的过程.请认真阅读并完成相应的任务.(10分)
解:方程两边同乘 ,得x2+x﹣12=x(x﹣3). ………第一步
去括号,得x2+x﹣12=x2﹣3x. ………第二步
移项、合并同类项,得4x=12. ………第三步
解得x=3. ………第四步
①第一步中“ ”处应为 ,这一步的目的是 .其依据是 ;
②小颖在反思上述解答过程时发现缺少了一步.请你补全这一步,并说明这一步不能缺少的理由.
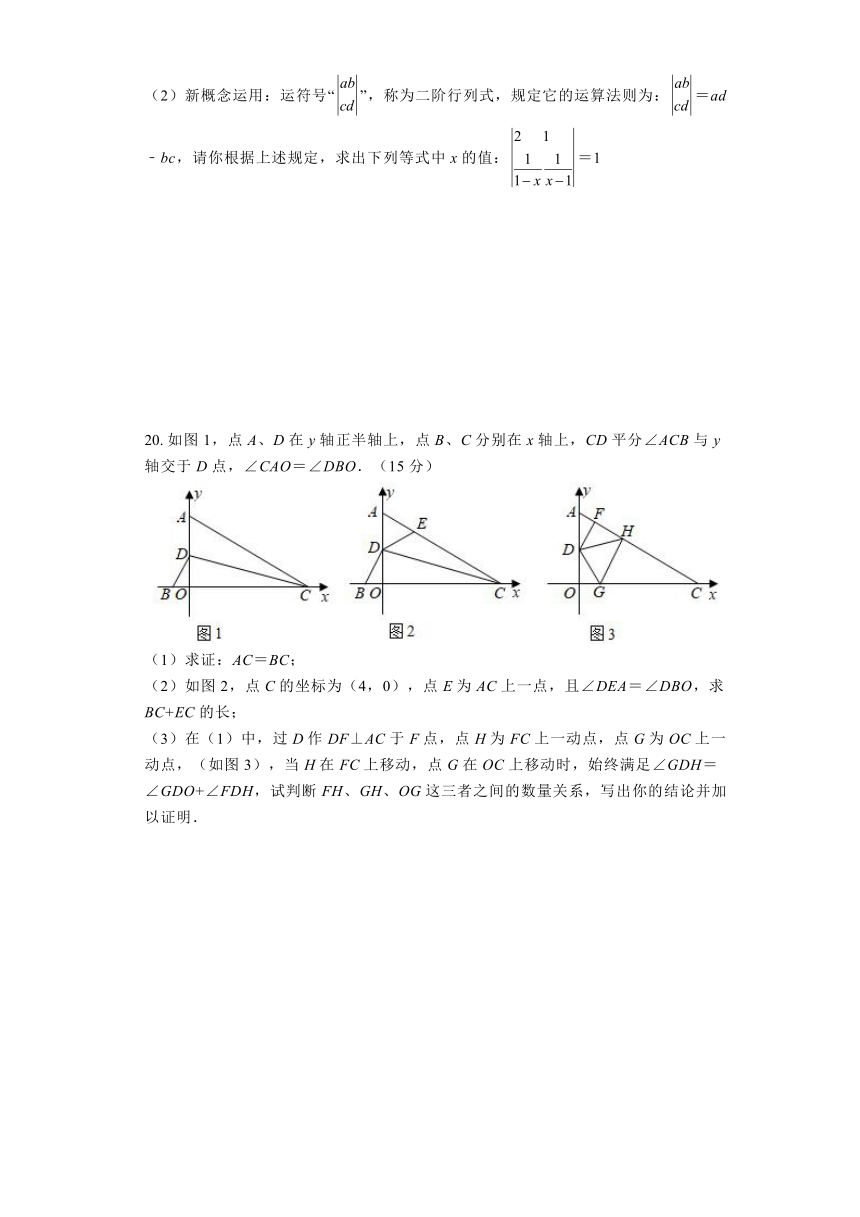
(2)新概念运用:运符号“”,称为二阶行列式,规定它的运算法则为:=ad﹣bc,请你根据上述规定,求出下列等式中x的值:=1
20. 如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=∠DBO.(15分)
(1)求证:AC=BC;
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;
(3)在(1)中,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,(如图3),当H在FC上移动,点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
数学参考答案(学生版)
1. 【答案】B
【分析】
根据轴对称图形的概念求解.
【详解】
解:A、不是轴对称图形,不符合题意;
B、是轴对称图形,符合题意;
C、不是轴对称图形,不符合题意;
D、不是轴对称图形,不符合题意;
故选:B.
2. 【答案】B
【分析】
根据分解因式的方法进行分解,同时分解到不能再分解为止;
【详解】
A、 ,故该选项错误;
B、 ,故该选项正确;
C、,故该选项错误;
D、,故该选项错误;
故选:B.
3. 【答案】C
【分析】
根据分式乘除法的法则和分式的基本性质解答即可.
【详解】
A、,故A错误;
B、,故B错误;
C、,故C正确;
D、,故D错误,
故选:C.
4. 【答案】A
【分析】
先将2a2+4ab+2b2分解因式,然后将a+b=3整体代入进行计算即可得.
【详解】
∵a+b=3,
∴2a2+4ab+2b2-6
=2(a2+2ab+b2)-6
=2(a+b)2-6
=2×32-6
=12,
故选A.
5. 【答案】C
【分析】
根据第一次进书的总钱数÷第一次购进套数=第二次进书的总钱数÷第二次购进套数列方程可得.
【详解】
若设书店第一次购进该科幻小说x套,
由题意列方程正确的是,
故选:C.
6. 【答案】B
【分析】
根据三角形的稳定性解答即可.
【详解】
人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:B.
7. 【答案】A
【分析】
根据三角形全等判定定理逐一判断即可.
【详解】
∵不符合任何一个判定定理,不能判定
∴A符合题意;
∵,符合SAS判定定理,能判定
∴B不符合题意;
∵,符合ASA判定定理,能判定
∴C不符合题意;
∵,符合AAS判定定理,能判定
∴D不符合题意;
故选A.
8. 【答案】C
【分析】
根据三角形内角和180求出∠BAC,再由AD是的角平分线求得∠DAC,最后利用直角三角形的两个锐角互余求出∠ADE,问题得到解决.
【详解】
解:∵,
∴,
∵是的角平分线,
∴,
∵,
∴,
故选:C.
9. 【答案】B
【分析】作GM⊥AB于M,如图,先利用基本作图得到AG平分∠BAC,再根据角平分线的性质得到GM=GH=2,然后根据三角形面积公式计算.
【详解】作GM⊥AB于M,如图,
由作法得AG平分∠BAC,
而GH⊥AC,GM⊥AB,
∴GM=GH=2,
∴S△ABG=×5×2=5.
故选:B.
10. 【答案】C
【分析】
证明△BDF≌△CDA可判断①;
由利用三角形的外角的性质及四边形的内角和定理可判断②;
连接利用DH是BC的垂直平分线,从而可判断③;
过G作GJ⊥AB于J,过F作FMBC于M,连接GM,设 分别计算三角形ADC的面积和四边形CEGH的面积可判断④;
由△BDF∽△CEF,可判断⑤.
【详解】
解:∵CD⊥AB,BF⊥AC,
∴∠BEC=∠BDC=∠ADC=90°,
∵∠ABC=45°,
∴∠DCB=45°=∠ABC,
∴BD=DC,
∵∠BDC=∠CEF=90°,∠DFB=∠EFC,
∴由三角形内角和定理得:∠DBF=∠ACD,
∵在△BDF和△CDA中,
∴△BDF≌△CDA(ASA),
∴BF=AC,∠BFD=∠A,∴①正确;
∵∠DFB=∠FBC+∠FCB=∠FBC+45°,∠DGF=∠GBD+45°,∠FBC=∠GBD,
∴∠DFG=∠DGF,
∴∠A=∠DGE,故②正确,
如图,连接
∵∠ABC=45°,∠BDC=90°,
∴△BDC是等腰直角三角形,
∵H是BC边的中点,
∴DH垂直平分BC,
故③正确;
过G作GJ⊥AB于J,过F作FMBC于M,连接GM,
平分
四边形DGMF是菱形,
设
则
四边形CFGH的面积=梯形GHMF的面积+的面积
S△ADCS四边形CEGH,故④错误.
∵△BDF∽△CEF,
∴,
∵BD=DC,CE=AE,DF=DG,
∴
∴DG AE=DC EF,故⑤正确.
故选:C.
11. 【答案】.
【详解】
试题分析:原式==.故答案为.
考点:因式分解-运用公式法.
12. 【答案】
【分析】
由已知条件可知xy≠0,根据分式的基本性质,先将分式的分子、分母同时除以xy,再把代入即可.
【详解】
解:∵
∴x≠0,y≠0,
∴xy≠0.
故答案为.
13. 【答案】4
【详解】
分析:根据全等三角形的性质得出DE=AB=2,EF=BC=4,根据三角形三边关系定理求出2<DF<6,即可得出答案.
详解:如图,
∵△ABC≌△DEF,AB=2,BC=4,
∴DE=AB=2,EF=BC=4,
∴4-2<DF<4+2,
∴2<DF<6,
∵DE=2,EF=4,△DEF的周长为偶数,
∴DF=4,
故答案为4.
点睛:本题考查了全等三角形的性质和三角形的三边关系定理的应用,注意:全等三角形的对应角相等,对应边相等.
14. 【答案】2或
【分析】
可分两种情况:①△ABP≌△PCQ得到BP=CQ,AB=PC,②△ABP≌△QCP得到BA=CQ,PB=PC,然后分别计算出t的值,进而得到v的值.
【详解】
解:①当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=8cm,
∴PC=8cm,
∴BP=12﹣8=4(cm),
∴2t=4,解得:t=2,
∴CQ=BP=4cm,
∴v×2=4,
解得:v=2;
②当BA=CQ,PB=PC时,△ABP≌△QCP,
∵PB=PC,
∴BP=PC=6cm,
∴2t=6,解得:t=3,
∵CQ=AB=8cm,
∴v×3=8,
解得:v=,
综上所述,当v=2或时,△ABP与△PQC全等,
故答案为:2或.
15. 【答案】1
【分析】
根据三角形的中线把三角形分成两个面积相等的三角形解答.
【详解】
解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×4=2cm2,
∴S△BCE=S△ABC=×4=2cm2,
∵点F是CE的中点,
∴S△BEF=S△BCE=×2=1cm2.
故答案为:1.
16. 【答案】(1)①;②;(2);-14
【分析】
(1)①先计算积的乘方,然后计算单项式乘单项式;
②先计算积的乘方,然后计算单项式除以单项式;
(2)整式的混合运算,先算乘法,然后再算加减合并同类项化简,最后代入求值.
【详解】
解:(1)①
=
;
②
=
=;
(2)
当时,原式.
17. 【答案】(1)证明见解析(2)证明见解析
【详解】
试题分析:(1)根据SSS推出≌,根据全等三角形的性质推出即可.
(2)根据全等三角形的性质推出 求出,根据平行线的判定推出即可.
试题解析: (1)∵在△ADE和△CBF中,
∴△ADE≌△CBF(SSS),
∴∠D=∠B.
(2)∵△ADE≌△CBF,
∴∠AED=∠CFB,
∵
∴∠AEO=∠CFO,
∴AE∥CF.
18. 【答案】(1)乙队单独完成需90天;(2)在不超过计划天数的前提下,由甲、乙合作完成最省钱.
【分析】
(1)求的是乙的工效,工作时间明显.一定是根据工作总量来列等量关系.等量关系为:甲20天的工作量+甲乙合作24天的工作总量=1.
(2)根据题意,分别求出三种情况的费用,然后把在工期内的情况进行比较即可.
【详解】
解:(1)设乙队单独完成需x天.
根据题意,得:.
解这个方程得:x=90.
经检验,x=90是原方程的解.
∴乙队单独完成需90天.
(2)设甲、乙合作完成需y天,则有,
解得,y=36;
①甲单独完成需付工程款为:60×3.5=210(万元).
②乙单独完成超过计划天数不符题意,
③甲、乙合作完成需付工程款为:36×(3.5+2)=198(万元).
答:在不超过计划天数的前提下,由甲、乙合作完成最省钱.
19. 【答案】(1)①x(x﹣3),去分母,等式的基本性质;②见解析,因为分式方程可能产生增根,所以分式方程必须检验;(2)4
【分析】
(1)①根据解分式方程的依据解答;②检验方程的解即可;
(2)根据新概念列分式方程计算即可.
【详解】
.解:(1)①∵分式方程的公分母为x(x﹣3),
∴第一步中“ ”处应为 x(x﹣3),这一步的目的是去分母,其依据是等式的基本性质,
故答案为:x(x﹣3),去分母,等式的基本性质;
②检验:当x=3时,x(x﹣3)=0,
∴x=3是原方程的增根,原方程无解.
理由:因为分式方程可能产生增根,所以分式方程必须检验.
(2)解:根据题中的新定义化简所求方程得:
,
分母得:2+1=x﹣1,
解得:x=4,
检验:当x=4时,x﹣1=3≠0,
∴x=4是分式方程的解,
故x的值为4.
20. 【答案】(1)证明见解析;(2)8;(3)GH=OG+FH,证明见解析
【分析】
(1)根据角平分线得出∠ACD=∠BCD,进而判断出△ACD≌△BCD,即可得出结论;
(2)过点D作DM⊥AC于M,根据角平分线得出DO=DM,进而判断出△BOD≌△AMD,得出OB=AM,进而判断出Rt△DOC≌Rt△DMC,得出OC=MC,再判断出OB=EM,即可得出结论;
(3)在GO的延长线上取一点N,使ON=FH,再判断出DO=DF,进而判断出△DON≌△DFH,得出DN=DH,∠ODN=∠FDH,进而判断出∠GDH=∠GDN,进而判断出△DGN≌△DGH,得出GH=GN,即可得出结论.
【详解】
解:(1)∵CD平分∠ACB,
∴∠ACD=∠BCD,
在△ACD和△BCD中,
,
∴△ACD≌△BCD(AAS),
∴AC=BC;
(2)如图2,过点D作DM⊥AC于M,
∵CD平分∠ACB,OD⊥BC,
∴DO=DM,
在△BOD和△AMD中,
,
∴△BOD≌△AMD(AAS),
∴OB=AM,
在Rt△DOC和Rt△DMC中,
,
∴Rt△DOC≌Rt△DMC,
∴OC=MC,
∵∠CAO=∠DBO,∠DEA=∠DBO,
∴∠DAE=∠DEA,
∵DM⊥AC,
∴AM=EM,
∴OB=EM,
∵C(4,0),
∴OC=4,
∴BC+CE=OB+OC+MC-EM=2OC=8;
(3)GH=OG+FH;
证明:如图3,在GO的延长线上取一点N,使ON=FH,
∵CD平分∠ACO,DF⊥AC,OD⊥OC,
∴DO=DF,
在△DON和△DFH中,
,
∴△DON≌△DFH(SAS),
∴DN=DH,∠ODN=∠FDH,
∵∠GDH=∠GDO+∠FDH,
∴∠GDH=∠GDO+∠ODN=∠GDN,
在△DGN和△DGH中,
,
∴△DGN≌△DGH(SAS),
∴GH=GN,
∵ON=FH,
∴GH=GN=OG+ON=OG+FH.
第 page number 页,共 number of pages 页
八年级数学
一、单选题(共40分)
1. 如图,四个图标分别是剑桥大学、北京大学、浙江大学和北京理工大学的校徽的重要组成部分,其中是轴对称图形的是( )
A. B.
C. D.
2. 下列分解因式正确的是( )
A. B.=
C. D.
3. 下列计算正确的是( )
A. B.
C. D.
4. 若a+b=3,则2a2+4ab+2b2-6的值是( )
A.12 B.6 C.3 D.0
5. 暑假期间,某科幻小说的销售量急剧上升.某书店分别用600元和800元两次购进该小说,第二次购进的数量比第一次多40套,且两次购书时,每套书的进价相同.若设书店第一次购进该科幻小说x套,由题意列方程正确的是( )
A. B.
C. D.
6. 如图,人字梯中间一般会设计一 “拉杆”,以增加使用梯子时的安全性这样做的道理是( )
A.两点之间的所有连线中线段最短
B.三角形具有稳定性
C.经过两点有一条直线,并且只有一条直线拉杆
D.在连接直线外一点与直线上各点的线段中,垂线段最短
7. 已知:如图,点D,E分别在,上,,添加一个条件,不能判定的是( )
A. B. C. D.
8. 如图,在中,是的角平分线,,若,则的度数为( )
A. B. C. D.
9. 如图,中,,,以点为圆心,任意长为半径作弧,分别交、于和,再分别以点、为圆心,大于二分之一为半径作弧,两弧交于点,连接并延长交于点,于,,则的面积为
A.4 B.5 C.9 D.10
10. 如图,△ABC中,∠ABC=45°,CD⊥AB于点D,BE平分∠ABC,且BE⊥AC于点E,与CD交于F,H是BC边的中点,连接DH与BE交于点G,则下列结论:
①BF=AC;②∠A=∠DGE;③CE<BG;④S△ADC=S四边形CEGH;⑤DG AE=DC EF中,正确结论的个数是( )
A.2 B.3 C.4 D.5
二、填空题(共25分)
11. 因式分解:4+12(x-y)+9(x-y)2= .
12. 已知﹣=3,则分式的值为 .
13. ≌,,,若的周长为偶数,则 .
14. 如图,在矩形ABCD中,AB=8cm,AD=12cm,点P从点B出发,以2cm/s的速度沿BC边向点C运动,到达点C停止,同时,点Q从点C出发,以vcm/s的速度沿CD边向点D运动,到达点D停止,规定其中一个动点停止运动时,另一个动点也随之停止运动.当v为 时,△ABP与△PCQ全等.
15. 如图,在△中,已知点分别为的中点,若△的面积为,则阴影部分的面积为
三、解答题(共55分)
16. (1)计算下列式子:(10分)
①= ;
②= .
(2) 先化简,再求值:,其中.
17. 如图,AC与BD交于点O,AD=CB,E、F是BD上两点,且AE=CF,DE=BF.(10分)
求证:(1)∠D=∠B;
(2)AE∥CF.
18. 在我市某一城市美化工程招标时,有甲、乙两个工程队投标,经测算:甲队单独完成这项工程需要60天,若由甲队先做20天,剩下的工程由甲、乙合作24天可完成.(10分)
(1)乙队单独完成这项工程需要多少天?
(2)甲队施工一天,需付工程款3.5万元,乙队施工一天需付工程款2万元.若该工程计划在70天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成工程省钱?还是由甲乙两队全程合作完成该工程省钱?
19. (1)下面是小颖同学解分式方程=1的过程.请认真阅读并完成相应的任务.(10分)
解:方程两边同乘 ,得x2+x﹣12=x(x﹣3). ………第一步
去括号,得x2+x﹣12=x2﹣3x. ………第二步
移项、合并同类项,得4x=12. ………第三步
解得x=3. ………第四步
①第一步中“ ”处应为 ,这一步的目的是 .其依据是 ;
②小颖在反思上述解答过程时发现缺少了一步.请你补全这一步,并说明这一步不能缺少的理由.
(2)新概念运用:运符号“”,称为二阶行列式,规定它的运算法则为:=ad﹣bc,请你根据上述规定,求出下列等式中x的值:=1
20. 如图1,点A、D在y轴正半轴上,点B、C分别在x轴上,CD平分∠ACB与y轴交于D点,∠CAO=∠DBO.(15分)
(1)求证:AC=BC;
(2)如图2,点C的坐标为(4,0),点E为AC上一点,且∠DEA=∠DBO,求BC+EC的长;
(3)在(1)中,过D作DF⊥AC于F点,点H为FC上一动点,点G为OC上一动点,(如图3),当H在FC上移动,点G在OC上移动时,始终满足∠GDH=∠GDO+∠FDH,试判断FH、GH、OG这三者之间的数量关系,写出你的结论并加以证明.
数学参考答案(学生版)
1. 【答案】B
【分析】
根据轴对称图形的概念求解.
【详解】
解:A、不是轴对称图形,不符合题意;
B、是轴对称图形,符合题意;
C、不是轴对称图形,不符合题意;
D、不是轴对称图形,不符合题意;
故选:B.
2. 【答案】B
【分析】
根据分解因式的方法进行分解,同时分解到不能再分解为止;
【详解】
A、 ,故该选项错误;
B、 ,故该选项正确;
C、,故该选项错误;
D、,故该选项错误;
故选:B.
3. 【答案】C
【分析】
根据分式乘除法的法则和分式的基本性质解答即可.
【详解】
A、,故A错误;
B、,故B错误;
C、,故C正确;
D、,故D错误,
故选:C.
4. 【答案】A
【分析】
先将2a2+4ab+2b2分解因式,然后将a+b=3整体代入进行计算即可得.
【详解】
∵a+b=3,
∴2a2+4ab+2b2-6
=2(a2+2ab+b2)-6
=2(a+b)2-6
=2×32-6
=12,
故选A.
5. 【答案】C
【分析】
根据第一次进书的总钱数÷第一次购进套数=第二次进书的总钱数÷第二次购进套数列方程可得.
【详解】
若设书店第一次购进该科幻小说x套,
由题意列方程正确的是,
故选:C.
6. 【答案】B
【分析】
根据三角形的稳定性解答即可.
【详解】
人字梯中间一般会设计一“拉杆”,是为了形成三角形,利用三角形具有稳定性来增加其稳定性,
故选:B.
7. 【答案】A
【分析】
根据三角形全等判定定理逐一判断即可.
【详解】
∵不符合任何一个判定定理,不能判定
∴A符合题意;
∵,符合SAS判定定理,能判定
∴B不符合题意;
∵,符合ASA判定定理,能判定
∴C不符合题意;
∵,符合AAS判定定理,能判定
∴D不符合题意;
故选A.
8. 【答案】C
【分析】
根据三角形内角和180求出∠BAC,再由AD是的角平分线求得∠DAC,最后利用直角三角形的两个锐角互余求出∠ADE,问题得到解决.
【详解】
解:∵,
∴,
∵是的角平分线,
∴,
∵,
∴,
故选:C.
9. 【答案】B
【分析】作GM⊥AB于M,如图,先利用基本作图得到AG平分∠BAC,再根据角平分线的性质得到GM=GH=2,然后根据三角形面积公式计算.
【详解】作GM⊥AB于M,如图,
由作法得AG平分∠BAC,
而GH⊥AC,GM⊥AB,
∴GM=GH=2,
∴S△ABG=×5×2=5.
故选:B.
10. 【答案】C
【分析】
证明△BDF≌△CDA可判断①;
由利用三角形的外角的性质及四边形的内角和定理可判断②;
连接利用DH是BC的垂直平分线,从而可判断③;
过G作GJ⊥AB于J,过F作FMBC于M,连接GM,设 分别计算三角形ADC的面积和四边形CEGH的面积可判断④;
由△BDF∽△CEF,可判断⑤.
【详解】
解:∵CD⊥AB,BF⊥AC,
∴∠BEC=∠BDC=∠ADC=90°,
∵∠ABC=45°,
∴∠DCB=45°=∠ABC,
∴BD=DC,
∵∠BDC=∠CEF=90°,∠DFB=∠EFC,
∴由三角形内角和定理得:∠DBF=∠ACD,
∵在△BDF和△CDA中,
∴△BDF≌△CDA(ASA),
∴BF=AC,∠BFD=∠A,∴①正确;
∵∠DFB=∠FBC+∠FCB=∠FBC+45°,∠DGF=∠GBD+45°,∠FBC=∠GBD,
∴∠DFG=∠DGF,
∴∠A=∠DGE,故②正确,
如图,连接
∵∠ABC=45°,∠BDC=90°,
∴△BDC是等腰直角三角形,
∵H是BC边的中点,
∴DH垂直平分BC,
故③正确;
过G作GJ⊥AB于J,过F作FMBC于M,连接GM,
平分
四边形DGMF是菱形,
设
则
四边形CFGH的面积=梯形GHMF的面积+的面积
S△ADCS四边形CEGH,故④错误.
∵△BDF∽△CEF,
∴,
∵BD=DC,CE=AE,DF=DG,
∴
∴DG AE=DC EF,故⑤正确.
故选:C.
11. 【答案】.
【详解】
试题分析:原式==.故答案为.
考点:因式分解-运用公式法.
12. 【答案】
【分析】
由已知条件可知xy≠0,根据分式的基本性质,先将分式的分子、分母同时除以xy,再把代入即可.
【详解】
解:∵
∴x≠0,y≠0,
∴xy≠0.
故答案为.
13. 【答案】4
【详解】
分析:根据全等三角形的性质得出DE=AB=2,EF=BC=4,根据三角形三边关系定理求出2<DF<6,即可得出答案.
详解:如图,
∵△ABC≌△DEF,AB=2,BC=4,
∴DE=AB=2,EF=BC=4,
∴4-2<DF<4+2,
∴2<DF<6,
∵DE=2,EF=4,△DEF的周长为偶数,
∴DF=4,
故答案为4.
点睛:本题考查了全等三角形的性质和三角形的三边关系定理的应用,注意:全等三角形的对应角相等,对应边相等.
14. 【答案】2或
【分析】
可分两种情况:①△ABP≌△PCQ得到BP=CQ,AB=PC,②△ABP≌△QCP得到BA=CQ,PB=PC,然后分别计算出t的值,进而得到v的值.
【详解】
解:①当BP=CQ,AB=PC时,△ABP≌△PCQ,
∵AB=8cm,
∴PC=8cm,
∴BP=12﹣8=4(cm),
∴2t=4,解得:t=2,
∴CQ=BP=4cm,
∴v×2=4,
解得:v=2;
②当BA=CQ,PB=PC时,△ABP≌△QCP,
∵PB=PC,
∴BP=PC=6cm,
∴2t=6,解得:t=3,
∵CQ=AB=8cm,
∴v×3=8,
解得:v=,
综上所述,当v=2或时,△ABP与△PQC全等,
故答案为:2或.
15. 【答案】1
【分析】
根据三角形的中线把三角形分成两个面积相等的三角形解答.
【详解】
解:∵点E是AD的中点,
∴S△ABE=S△ABD,S△ACE=S△ADC,
∴S△ABE+S△ACE=S△ABC=×4=2cm2,
∴S△BCE=S△ABC=×4=2cm2,
∵点F是CE的中点,
∴S△BEF=S△BCE=×2=1cm2.
故答案为:1.
16. 【答案】(1)①;②;(2);-14
【分析】
(1)①先计算积的乘方,然后计算单项式乘单项式;
②先计算积的乘方,然后计算单项式除以单项式;
(2)整式的混合运算,先算乘法,然后再算加减合并同类项化简,最后代入求值.
【详解】
解:(1)①
=
;
②
=
=;
(2)
当时,原式.
17. 【答案】(1)证明见解析(2)证明见解析
【详解】
试题分析:(1)根据SSS推出≌,根据全等三角形的性质推出即可.
(2)根据全等三角形的性质推出 求出,根据平行线的判定推出即可.
试题解析: (1)∵在△ADE和△CBF中,
∴△ADE≌△CBF(SSS),
∴∠D=∠B.
(2)∵△ADE≌△CBF,
∴∠AED=∠CFB,
∵
∴∠AEO=∠CFO,
∴AE∥CF.
18. 【答案】(1)乙队单独完成需90天;(2)在不超过计划天数的前提下,由甲、乙合作完成最省钱.
【分析】
(1)求的是乙的工效,工作时间明显.一定是根据工作总量来列等量关系.等量关系为:甲20天的工作量+甲乙合作24天的工作总量=1.
(2)根据题意,分别求出三种情况的费用,然后把在工期内的情况进行比较即可.
【详解】
解:(1)设乙队单独完成需x天.
根据题意,得:.
解这个方程得:x=90.
经检验,x=90是原方程的解.
∴乙队单独完成需90天.
(2)设甲、乙合作完成需y天,则有,
解得,y=36;
①甲单独完成需付工程款为:60×3.5=210(万元).
②乙单独完成超过计划天数不符题意,
③甲、乙合作完成需付工程款为:36×(3.5+2)=198(万元).
答:在不超过计划天数的前提下,由甲、乙合作完成最省钱.
19. 【答案】(1)①x(x﹣3),去分母,等式的基本性质;②见解析,因为分式方程可能产生增根,所以分式方程必须检验;(2)4
【分析】
(1)①根据解分式方程的依据解答;②检验方程的解即可;
(2)根据新概念列分式方程计算即可.
【详解】
.解:(1)①∵分式方程的公分母为x(x﹣3),
∴第一步中“ ”处应为 x(x﹣3),这一步的目的是去分母,其依据是等式的基本性质,
故答案为:x(x﹣3),去分母,等式的基本性质;
②检验:当x=3时,x(x﹣3)=0,
∴x=3是原方程的增根,原方程无解.
理由:因为分式方程可能产生增根,所以分式方程必须检验.
(2)解:根据题中的新定义化简所求方程得:
,
分母得:2+1=x﹣1,
解得:x=4,
检验:当x=4时,x﹣1=3≠0,
∴x=4是分式方程的解,
故x的值为4.
20. 【答案】(1)证明见解析;(2)8;(3)GH=OG+FH,证明见解析
【分析】
(1)根据角平分线得出∠ACD=∠BCD,进而判断出△ACD≌△BCD,即可得出结论;
(2)过点D作DM⊥AC于M,根据角平分线得出DO=DM,进而判断出△BOD≌△AMD,得出OB=AM,进而判断出Rt△DOC≌Rt△DMC,得出OC=MC,再判断出OB=EM,即可得出结论;
(3)在GO的延长线上取一点N,使ON=FH,再判断出DO=DF,进而判断出△DON≌△DFH,得出DN=DH,∠ODN=∠FDH,进而判断出∠GDH=∠GDN,进而判断出△DGN≌△DGH,得出GH=GN,即可得出结论.
【详解】
解:(1)∵CD平分∠ACB,
∴∠ACD=∠BCD,
在△ACD和△BCD中,
,
∴△ACD≌△BCD(AAS),
∴AC=BC;
(2)如图2,过点D作DM⊥AC于M,
∵CD平分∠ACB,OD⊥BC,
∴DO=DM,
在△BOD和△AMD中,
,
∴△BOD≌△AMD(AAS),
∴OB=AM,
在Rt△DOC和Rt△DMC中,
,
∴Rt△DOC≌Rt△DMC,
∴OC=MC,
∵∠CAO=∠DBO,∠DEA=∠DBO,
∴∠DAE=∠DEA,
∵DM⊥AC,
∴AM=EM,
∴OB=EM,
∵C(4,0),
∴OC=4,
∴BC+CE=OB+OC+MC-EM=2OC=8;
(3)GH=OG+FH;
证明:如图3,在GO的延长线上取一点N,使ON=FH,
∵CD平分∠ACO,DF⊥AC,OD⊥OC,
∴DO=DF,
在△DON和△DFH中,
,
∴△DON≌△DFH(SAS),
∴DN=DH,∠ODN=∠FDH,
∵∠GDH=∠GDO+∠FDH,
∴∠GDH=∠GDO+∠ODN=∠GDN,
在△DGN和△DGH中,
,
∴△DGN≌△DGH(SAS),
∴GH=GN,
∵ON=FH,
∴GH=GN=OG+ON=OG+FH.
第 page number 页,共 number of pages 页
同课章节目录
