物理人教(2019)选择性必修第三册2.2.2 气体的等温变化(共19张ppt)
文档属性
| 名称 | 物理人教(2019)选择性必修第三册2.2.2 气体的等温变化(共19张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 517.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-13 16:24:03 | ||
图片预览






文档简介
(共19张PPT)
1.玻意耳定律的内容是什么?
复习回顾
2.等温变化公式是怎样的?
3.等温变化的图像是怎样的?
选择性必修第三册第二章 气体、液体和固体
专题:封闭气体压强的计算
2.2-2 气体的等温变化
学习目标:
1.会计算液体封闭气体的压强
2.会计算活塞、气缸密闭气体压强
3.会应用玻意尔定律分析分析解决问题
液体压强公式:
一、平衡态下液体封闭气体压强的计算
h
A
p = gh
p = p0 + gh
h
液面与外界大气相通,液面下h处的压强为:
①
h
h
②
h
③
【例】下列各图装置均处于静止状态。设大气压强为P0,用长为h的水银柱把一定质量的气体封闭在玻璃管中。求被封闭气体的压强P
p1 = p0
p2 = p0 + gh
p3 =p0- gh
【例】一上端开口、下端封闭的细长玻璃管用水银柱封闭一段气体。初始时玻璃管竖直放置,各段长度如图所示。现将玻璃管缓慢倒置过来,水银未流出管口。已知大气压强为p0=75cmHg,环境温度不变,则此时气体的长度为多少?
初态:
末态:
定律方程:
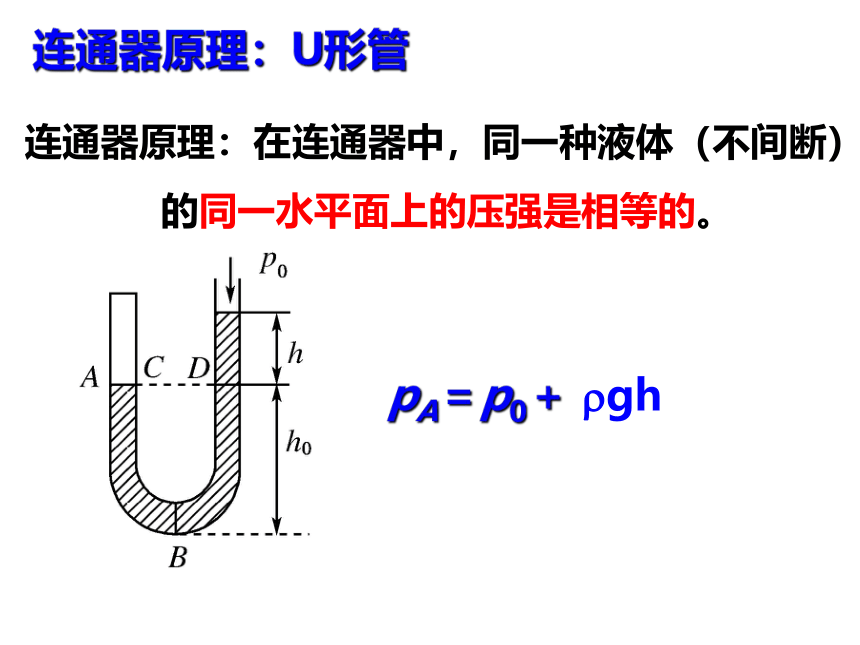
连通器原理:U形管
pA=p0+ gh
连通器原理:在连通器中,同一种液体(不间断)
的同一水平面上的压强是相等的。
h
④
h
⑤
h
⑥
连通器原理:同种液体中同一高度压强相等
p=p0+ gh
p =p0- gh
p =p0- gh
连通器原理:U形管
【例1】粗细均匀的玻璃管,一端封闭,长为12cm。一人手持玻璃管开口竖直向下潜入水中,当潜到水下某深度时看到水进入玻璃管口2cm,如图所示。求管口距液面的深度.(取水面上大气压强为p0=1.0×105Pa,g取10m/s2,池水中温度恒定)
【例2】水银气压计中混入一个气泡,上升到水银柱的上方,使水银柱上方不再是真空。当实际大气压相当于768mm高的水银柱产生的压强时,这个水银气压计的读数只有750mm,此时管中的水银面到管顶的距离为80mm。当这个气压计的读数为740mm水银柱时,实际的大气压相当于多高的水银柱产生的压强?设温度保持不变。
课本25页第4题
【例2】解析:一管中封闭气体为研究对象,设玻璃管的横截
面积为S,前后为等温变化。
初态:
p1=(768-750)mmHg=18mmHg
V1= SL1
末态:
p2=( p -740)mmHg
V2= S L2
等温变化,根据 p1V1=p2V2
解得: p=756mmHg
求用固体(如活塞等)封闭在静止容器内的气体压强,应对固体(如活塞等)进行受力分析。然后根据平衡条件求解。
二、平衡态下活塞密闭气体压强的计算
【例2】如图所示,导热性能良好的汽缸开口向上,用轻质活塞封闭着体积为V0的理想气体,外界大气压强为p0,环境温度保持不变,轻质活塞横截面积为S,与汽缸之间的摩擦不计.现在活塞上面放一质量为m的物块,活塞缓慢下移,并最终静止在某一位置.重力加速度为g.求:(1) 活塞静止时,缸内气体的压强;(2) 静止时活塞离汽缸底端的距离.
【检2】如下图(a)所示,一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2×10-3m2、质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,大气压强p0=1.0×105Pa。现将气缸竖直放置,如图(b)所示,取g=10m/s2 。求活塞与气缸底部之间的距离.
解:以缸内封闭气体为研究对象
初态:
末态:
由活塞受力平衡得:
【检2】
解得 L2=20cm
【检3】有一导热良好的圆柱形气缸置于水平地面上,并用一光滑的质量为M的活塞密封一定质量的理想气体,活塞面积为S.开始时汽缸开口向上,已知外界大气压强p0,被封气体的体积V1.求:
(1)被封气体的压强p1;
(2)现将汽缸倒置(如图二),活塞与地面间的气体始终与外界大气相通,待系统重新稳定后,活塞移动的距离△h是多少.
【检4】(多选)如图所示,活塞质量为m,缸套质量为M,通过弹簧吊在天花板上,气缸内封住了一定质量的空气,而活塞与缸套间无摩擦,活塞面积为S,大气压强为P0,过程中温度一直不变,则下列说法正确的是( )
AC
【检5】如图,一粗细均匀的细管开口向上竖直放置,管内有一段高度为2.0cm的水银柱,水银柱下密封了一定量的理想气体,水银柱上表面到管口的距离为2.0cm。若将细管倒置,水银柱下表面恰好位于管口处,且无水银滴落,管内气体温度与环境温度相同。已知大气压强为76cmHg 。求:细管的长度.
【拓展训练】如图所示,竖直放置的U形管,左端开口,右端封闭,管内有a、b两段水银柱,将A、B两段空气柱封闭在管内。已知水银柱a长为10 cm,水银柱b两个液面间的高度差为5 cm,大气压强为75 cmHg,求空气柱A、B产生的压强。
1.玻意耳定律的内容是什么?
复习回顾
2.等温变化公式是怎样的?
3.等温变化的图像是怎样的?
选择性必修第三册第二章 气体、液体和固体
专题:封闭气体压强的计算
2.2-2 气体的等温变化
学习目标:
1.会计算液体封闭气体的压强
2.会计算活塞、气缸密闭气体压强
3.会应用玻意尔定律分析分析解决问题
液体压强公式:
一、平衡态下液体封闭气体压强的计算
h
A
p = gh
p = p0 + gh
h
液面与外界大气相通,液面下h处的压强为:
①
h
h
②
h
③
【例】下列各图装置均处于静止状态。设大气压强为P0,用长为h的水银柱把一定质量的气体封闭在玻璃管中。求被封闭气体的压强P
p1 = p0
p2 = p0 + gh
p3 =p0- gh
【例】一上端开口、下端封闭的细长玻璃管用水银柱封闭一段气体。初始时玻璃管竖直放置,各段长度如图所示。现将玻璃管缓慢倒置过来,水银未流出管口。已知大气压强为p0=75cmHg,环境温度不变,则此时气体的长度为多少?
初态:
末态:
定律方程:
连通器原理:U形管
pA=p0+ gh
连通器原理:在连通器中,同一种液体(不间断)
的同一水平面上的压强是相等的。
h
④
h
⑤
h
⑥
连通器原理:同种液体中同一高度压强相等
p=p0+ gh
p =p0- gh
p =p0- gh
连通器原理:U形管
【例1】粗细均匀的玻璃管,一端封闭,长为12cm。一人手持玻璃管开口竖直向下潜入水中,当潜到水下某深度时看到水进入玻璃管口2cm,如图所示。求管口距液面的深度.(取水面上大气压强为p0=1.0×105Pa,g取10m/s2,池水中温度恒定)
【例2】水银气压计中混入一个气泡,上升到水银柱的上方,使水银柱上方不再是真空。当实际大气压相当于768mm高的水银柱产生的压强时,这个水银气压计的读数只有750mm,此时管中的水银面到管顶的距离为80mm。当这个气压计的读数为740mm水银柱时,实际的大气压相当于多高的水银柱产生的压强?设温度保持不变。
课本25页第4题
【例2】解析:一管中封闭气体为研究对象,设玻璃管的横截
面积为S,前后为等温变化。
初态:
p1=(768-750)mmHg=18mmHg
V1= SL1
末态:
p2=( p -740)mmHg
V2= S L2
等温变化,根据 p1V1=p2V2
解得: p=756mmHg
求用固体(如活塞等)封闭在静止容器内的气体压强,应对固体(如活塞等)进行受力分析。然后根据平衡条件求解。
二、平衡态下活塞密闭气体压强的计算
【例2】如图所示,导热性能良好的汽缸开口向上,用轻质活塞封闭着体积为V0的理想气体,外界大气压强为p0,环境温度保持不变,轻质活塞横截面积为S,与汽缸之间的摩擦不计.现在活塞上面放一质量为m的物块,活塞缓慢下移,并最终静止在某一位置.重力加速度为g.求:(1) 活塞静止时,缸内气体的压强;(2) 静止时活塞离汽缸底端的距离.
【检2】如下图(a)所示,一导热性能良好、内壁光滑的气缸水平放置,横截面积为S=2×10-3m2、质量为m=4kg厚度不计的活塞与气缸底部之间封闭了一部分气体,此时活塞与气缸底部之间的距离为24cm,大气压强p0=1.0×105Pa。现将气缸竖直放置,如图(b)所示,取g=10m/s2 。求活塞与气缸底部之间的距离.
解:以缸内封闭气体为研究对象
初态:
末态:
由活塞受力平衡得:
【检2】
解得 L2=20cm
【检3】有一导热良好的圆柱形气缸置于水平地面上,并用一光滑的质量为M的活塞密封一定质量的理想气体,活塞面积为S.开始时汽缸开口向上,已知外界大气压强p0,被封气体的体积V1.求:
(1)被封气体的压强p1;
(2)现将汽缸倒置(如图二),活塞与地面间的气体始终与外界大气相通,待系统重新稳定后,活塞移动的距离△h是多少.
【检4】(多选)如图所示,活塞质量为m,缸套质量为M,通过弹簧吊在天花板上,气缸内封住了一定质量的空气,而活塞与缸套间无摩擦,活塞面积为S,大气压强为P0,过程中温度一直不变,则下列说法正确的是( )
AC
【检5】如图,一粗细均匀的细管开口向上竖直放置,管内有一段高度为2.0cm的水银柱,水银柱下密封了一定量的理想气体,水银柱上表面到管口的距离为2.0cm。若将细管倒置,水银柱下表面恰好位于管口处,且无水银滴落,管内气体温度与环境温度相同。已知大气压强为76cmHg 。求:细管的长度.
【拓展训练】如图所示,竖直放置的U形管,左端开口,右端封闭,管内有a、b两段水银柱,将A、B两段空气柱封闭在管内。已知水银柱a长为10 cm,水银柱b两个液面间的高度差为5 cm,大气压强为75 cmHg,求空气柱A、B产生的压强。
同课章节目录
- 第一章 分子动理论
- 1 分子动理论的基本内容
- 2 实验:用油膜法估测油酸分子的大小
- 3 分子运动速率分布规律
- 4 分子动能和分子势能
- 第二章 气体、固体和液体
- 1 温度和温标
- 2 气体的等温变化
- 3 气体的等压变化和等容变化
- 4 固体
- 5 液体
- 第三章 热力学定律
- 1 功、热和内能的改变
- 2 热力学第一定律
- 3 能量守恒定律
- 4 热力学第二定律
- 第四章 原子结构和波粒二象性
- 1 普朗克黑体辐射理论
- 2 光电效应
- 3 原子的核式结构模型
- 4 氢原子光谱和玻尔的原子模型
- 5 粒子的波动性和量子力学的建立
- 第五章 原子核
- 1 原子核的组成
- 2 放射性元素的衰变
- 3 核力与结合能
- 4 核裂变与核聚变
- 5 “基本”粒子
