六年级下册数学人教版 4.1.3 解比例(课件(14张ppt)
文档属性
| 名称 | 六年级下册数学人教版 4.1.3 解比例(课件(14张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 4.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 10:16:09 | ||
图片预览






文档简介
(共14张PPT)
一、复习导入
1、什么是比例的基本性质?
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
2、根据比例的基本性质判断下面的比能否组成比例。
18:20 和 7.2:8 2:10 和 1.6:8
18×8=144
20×7.2=144
因为144=144,所以18:20=7.2:8
2×8=16
10×1.6=16
因为16=16,所以2:10=1.6:8
3、谁能很快说出下面比例中缺少的项各是几?
14:21=2:( ) 1.25:( )=2.5:4
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的那个未知项。
求比例中的未知项,叫作解比例。
3、解比例
二、探究新知
2
长征五号运载火箭总长约为57 m。有一个长征五号运载火箭的模型,它的总长与火箭总长的比是1∶10。这个模型总长约为多少米
(1)题中已知条件和所求问题各是什么?
(2)划线句子含有的等量关系是什么?
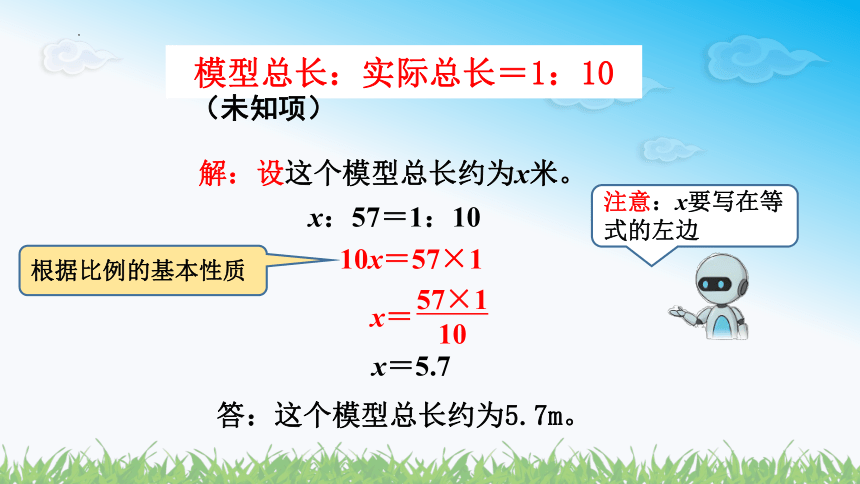
模型总长:实际总长=1:10
解:设这个模型总长约为x米。
模型总长:实际总长=1:10
x:57=1:10
10x=57×1
x=5.7
答:这个模型总长约为5.7m。
注意:x要写在等式的左边
(未知项)
x=
57×1
10
根据比例的基本性质
解:设这个模型总长约为x米。
x:57=1:10
10x=57×1
x=5.7
答:这个模型总长约为5.7m。
x=
57×1
10
回顾与反思
x=5.7,这个答案对吗?怎么检验呢?
5.7:57=
1
10
1:10=
1
10
比值相等,能组成比例
归纳总结
解比例时,先根据比例的基本性质把比例转化成方程,再按解方程的方法进行解答。
注意通常把含有未知项的积放在等号的左边,这样便于计算。计算时一般写成两个数的积除以一个数的分数形式,这样便于约分,先约分再计算比较简便。
3
解比例
2.4
1.5
=
6
x
这个比例的内项和外项分别是什么?
2.4和x是外项,
1.5和6是外项。
解:
2.4x=1.5×6
x=
1.5×6
2.4
1
0.4
x=
15
4
三、巩固练习
1、解比例。
x:10= :
1
4
1
3
0.4:x=1.2:2
3
x
=
12
2.4
解:
x=10×
1
4
1
3
x=
5
2
1
3
x= ÷
5
2
1
3
x=
15
2
解:
1.2x=0.4×2
1.2x=0.8
x=0.8÷1.2
x=
2
3
解:
12x=2.4×3
12x=7.2
x=7.2÷12
x=0.6
2、餐馆给餐具消毒,要用100mL消毒液配成消毒水,如果消毒液与水的比是1∶150,应加入多少升水?
解:设应加入x 毫升水。
100:x=1:150
x=100×150
x=1500
消毒液:水=1:150
答:应加入1.5升水。
1500 毫升=1.5升
3、相同质量的水和冰的体积之比是9∶10。一块体积是50 dm3的冰,化成水后的体积是多少?
水的体积:冰的体积=9:10
解:设化成水后的体积是x 立方分米。
x:50:=9:10
10 x=9×50
x=450÷10
x=45
答:化成水后的体积是45立方分米。
4、按照下面的条件列出比例,并且解比例。
(1)5与8的比等于40与x的比。
(2)x与 的比等于 与 的比。
3
4
2
5
1
5
(3)比例的两个内项分别是2和5,两个外项分别是x和2.5。
四、课堂总结
这节课你们学会了什么知识?
解比例
求比例中的未知项,叫作解比例。
解:设这个模型总长约为x米。
x:57=1:10
10x=57×1
x=5.7
答:这个模型总长约为5.7m。
x=
57×1
10
2.4
1.5
=
6
x
解:
2.4x=1.5×6
x=
1.5×6
2.4
1
0.4
x=
15
4
模型总长:实际总长=1:10
一、复习导入
1、什么是比例的基本性质?
在比例里,两个外项的积等于两个内项的积。
这叫做比例的基本性质。
2、根据比例的基本性质判断下面的比能否组成比例。
18:20 和 7.2:8 2:10 和 1.6:8
18×8=144
20×7.2=144
因为144=144,所以18:20=7.2:8
2×8=16
10×1.6=16
因为16=16,所以2:10=1.6:8
3、谁能很快说出下面比例中缺少的项各是几?
14:21=2:( ) 1.25:( )=2.5:4
根据比例的基本性质,如果已知比例中的任何三项,就可以求出这个比例中的那个未知项。
求比例中的未知项,叫作解比例。
3、解比例
二、探究新知
2
长征五号运载火箭总长约为57 m。有一个长征五号运载火箭的模型,它的总长与火箭总长的比是1∶10。这个模型总长约为多少米
(1)题中已知条件和所求问题各是什么?
(2)划线句子含有的等量关系是什么?
模型总长:实际总长=1:10
解:设这个模型总长约为x米。
模型总长:实际总长=1:10
x:57=1:10
10x=57×1
x=5.7
答:这个模型总长约为5.7m。
注意:x要写在等式的左边
(未知项)
x=
57×1
10
根据比例的基本性质
解:设这个模型总长约为x米。
x:57=1:10
10x=57×1
x=5.7
答:这个模型总长约为5.7m。
x=
57×1
10
回顾与反思
x=5.7,这个答案对吗?怎么检验呢?
5.7:57=
1
10
1:10=
1
10
比值相等,能组成比例
归纳总结
解比例时,先根据比例的基本性质把比例转化成方程,再按解方程的方法进行解答。
注意通常把含有未知项的积放在等号的左边,这样便于计算。计算时一般写成两个数的积除以一个数的分数形式,这样便于约分,先约分再计算比较简便。
3
解比例
2.4
1.5
=
6
x
这个比例的内项和外项分别是什么?
2.4和x是外项,
1.5和6是外项。
解:
2.4x=1.5×6
x=
1.5×6
2.4
1
0.4
x=
15
4
三、巩固练习
1、解比例。
x:10= :
1
4
1
3
0.4:x=1.2:2
3
x
=
12
2.4
解:
x=10×
1
4
1
3
x=
5
2
1
3
x= ÷
5
2
1
3
x=
15
2
解:
1.2x=0.4×2
1.2x=0.8
x=0.8÷1.2
x=
2
3
解:
12x=2.4×3
12x=7.2
x=7.2÷12
x=0.6
2、餐馆给餐具消毒,要用100mL消毒液配成消毒水,如果消毒液与水的比是1∶150,应加入多少升水?
解:设应加入x 毫升水。
100:x=1:150
x=100×150
x=1500
消毒液:水=1:150
答:应加入1.5升水。
1500 毫升=1.5升
3、相同质量的水和冰的体积之比是9∶10。一块体积是50 dm3的冰,化成水后的体积是多少?
水的体积:冰的体积=9:10
解:设化成水后的体积是x 立方分米。
x:50:=9:10
10 x=9×50
x=450÷10
x=45
答:化成水后的体积是45立方分米。
4、按照下面的条件列出比例,并且解比例。
(1)5与8的比等于40与x的比。
(2)x与 的比等于 与 的比。
3
4
2
5
1
5
(3)比例的两个内项分别是2和5,两个外项分别是x和2.5。
四、课堂总结
这节课你们学会了什么知识?
解比例
求比例中的未知项,叫作解比例。
解:设这个模型总长约为x米。
x:57=1:10
10x=57×1
x=5.7
答:这个模型总长约为5.7m。
x=
57×1
10
2.4
1.5
=
6
x
解:
2.4x=1.5×6
x=
1.5×6
2.4
1
0.4
x=
15
4
模型总长:实际总长=1:10
