2022-2023学年 北师大版八年级数学下册第一章 三角形的证明课后同步练习(无答案)
文档属性
| 名称 | 2022-2023学年 北师大版八年级数学下册第一章 三角形的证明课后同步练习(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 218.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 12:59:47 | ||
图片预览

文档简介
第一章 三角形的证明课后同步练习
班级:________ 姓名:________
一、单选题(共 8 小题)
1、如图,中,,于D ,于E,下列结论不成立的是( )
A. B. C. D.
2、如图,是等边三角形,D是BC边上一点,于点E.若,则DC的长为( )
A.4 B.5 C.6 D.7
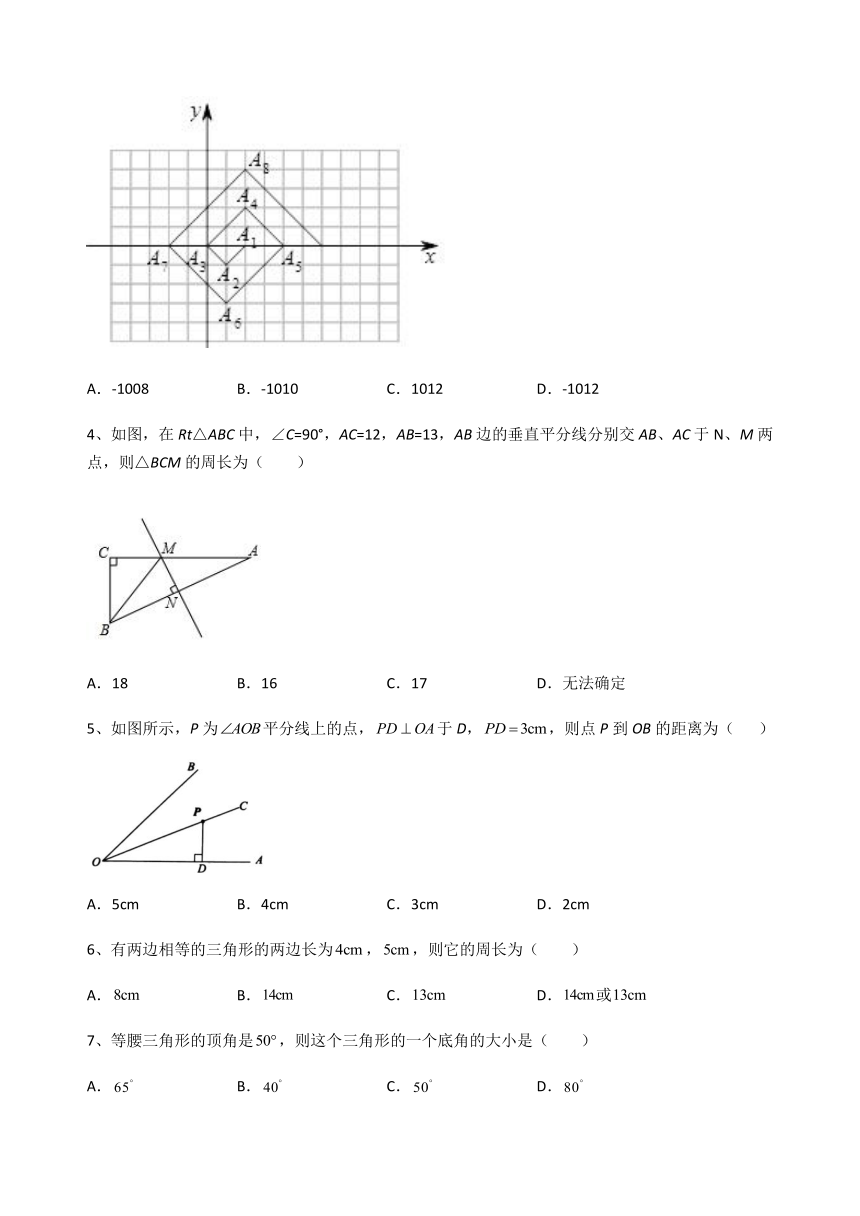
3、如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,,是斜边在x轴上,斜边长分别为2,4,6,...的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2021的横坐标为( )
A.-1008 B.-1010 C.1012 D.-1012
4、如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
A.18 B.16 C.17 D.无法确定
5、如图所示,P为平分线上的点,于D,,则点P到OB的距离为( )
A.5cm B.4cm C.3cm D.2cm
6、有两边相等的三角形的两边长为,,则它的周长为( )
A. B. C. D.或
7、等腰三角形的顶角是,则这个三角形的一个底角的大小是( )
A. B. C. D.
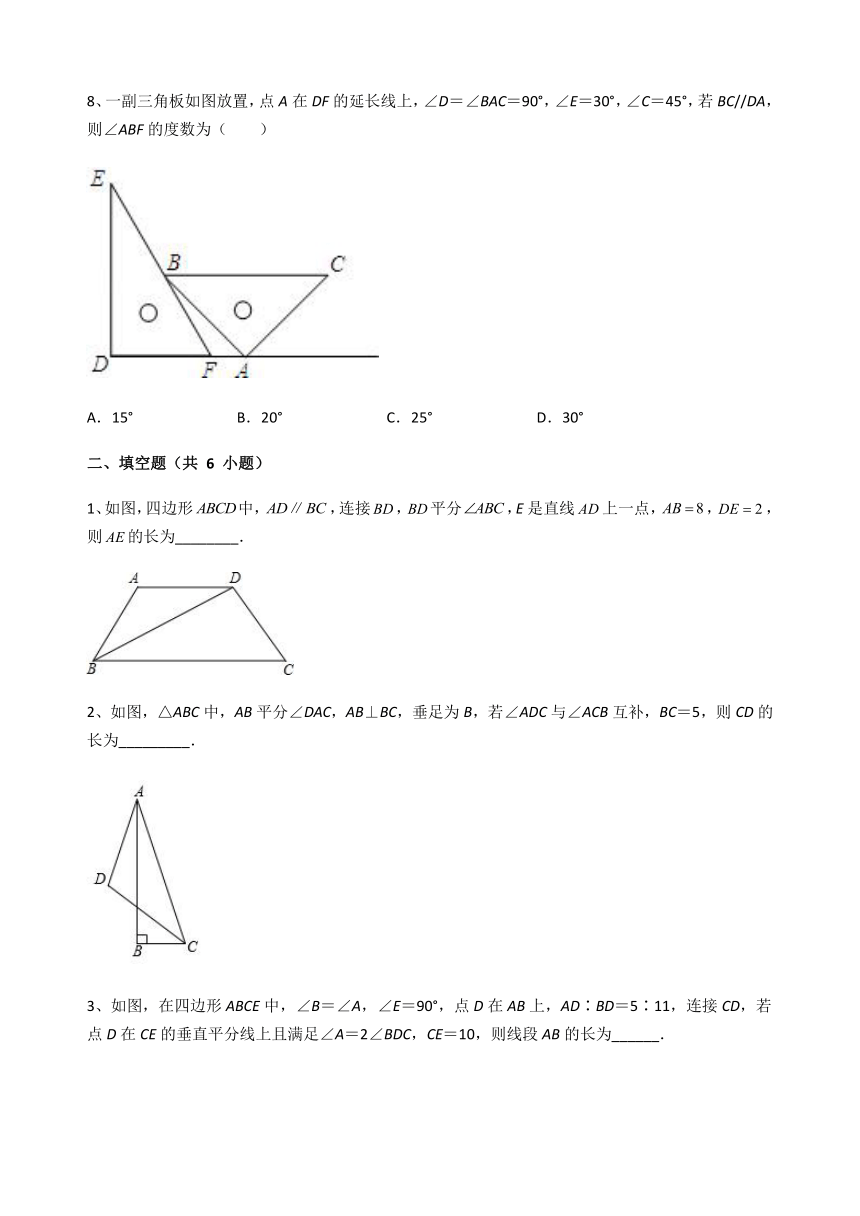
8、一副三角板如图放置,点A在DF的延长线上,∠D=∠BAC=90°,∠E=30°,∠C=45°,若BC//DA,则∠ABF的度数为( )
A.15° B.20° C.25° D.30°
二、填空题(共 6 小题)
1、如图,四边形中,,连接,平分,E是直线上一点,,,则的长为________.
2、如图,△ABC中,AB平分∠DAC,AB⊥BC,垂足为B,若∠ADC与∠ACB互补,BC=5,则CD的长为_________.
3、如图,在四边形ABCE中,∠B=∠A,∠E=90°,点D在AB上,AD∶BD=5∶11,连接CD,若点D在CE的垂直平分线上且满足∠A=2∠BDC,CE=10,则线段AB的长为______.
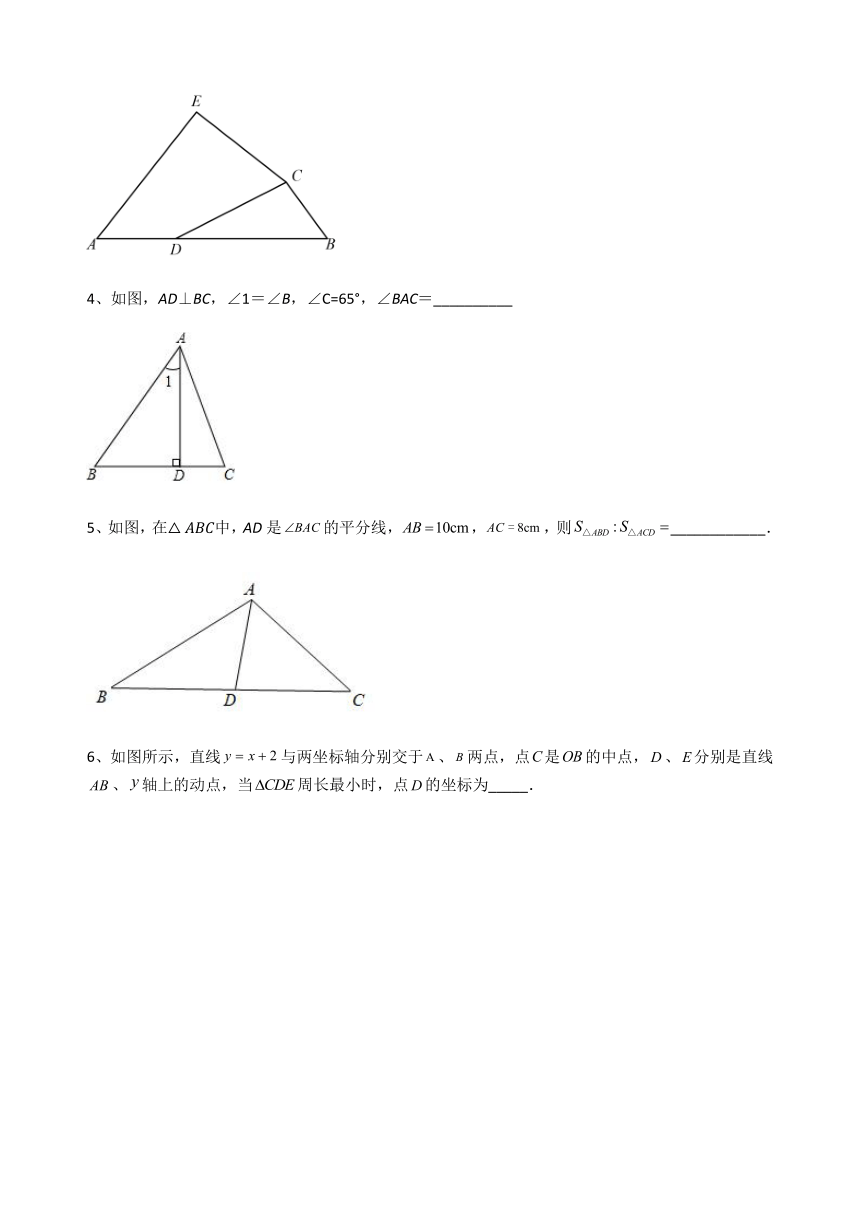
4、如图,AD⊥BC,∠1=∠B,∠C=65°,∠BAC=__________
5、如图,在中,AD是的平分线,,,则____________.
6、如图所示,直线与两坐标轴分别交于、两点,点是的中点,、分别是直线、轴上的动点,当周长最小时,点的坐标为_____.
三、解答题(共 5 小题)
1、如图,在中,,,.
(1)的面积等于_______;
(2)为线段上一点,过点作,垂足为.当时,请在如图所示的矩形区域内,用无刻度的直尺和圆规,画出线段,并简要说明点和点的位置是如何找到的(保留作图痕迹,不要求证明).
2、如图,是等边三角形,,分别交AB,AC于点D,E.
(1)求证:是等边三角形;
(2)点F在线段DE上,点G在外,,,求证:.
3、2021年10月10日是辛亥革命110周年纪念日.为进一步弘扬辛亥革命中体现的中华民族的伟大革命精神,社区开展了系列纪念活动.如图,有一块四边形空地,社区计划将其布置成展区,陈列有关辛亥革命的历史图片.现测得,,,且.
(1)试说明;
(2)求四边形展区(阴影部分)的面积.
4、设两个点A、B的坐标分别为,,则线段AB的长度为:.举例如下:A、B两点的坐标是,,则A、B两点之间的距离.请利用上述知识解决下列问题:
(1)若,,且,求x的值;
(2)已知△ABC,点A为、点B为、点C为,求△ABC的面积;
(3)求代数式的最小值.
5、如图,在△ABC中,AC=BC,∠ACB=90°,点D是边AB上的动点,连接CD,点B关于直线CD的对称点为点E,射线AE与射线CD交于点F.
(1)在图中,依题意补全图形;
(2)记∠DCB=α(α<45°),求∠BAF的大小;(用含α的式子表示)
(3)若△BCE是等边三角形,猜想EF和AB的数量关系,并证明你的结论.
班级:________ 姓名:________
一、单选题(共 8 小题)
1、如图,中,,于D ,于E,下列结论不成立的是( )
A. B. C. D.
2、如图,是等边三角形,D是BC边上一点,于点E.若,则DC的长为( )
A.4 B.5 C.6 D.7
3、如图,在一个单位为1的方格纸上,△A1A2A3,△A3A4A5,△A5A6A7,,是斜边在x轴上,斜边长分别为2,4,6,...的等腰直角三角形.若△A1A2A3的顶点坐标分别为A1(2,0),A2(1,-1),A3(0,0),则依图中所示规律,A2021的横坐标为( )
A.-1008 B.-1010 C.1012 D.-1012
4、如图,在Rt△ABC中,∠C=90°,AC=12,AB=13,AB边的垂直平分线分别交AB、AC于N、M两点,则△BCM的周长为( )
A.18 B.16 C.17 D.无法确定
5、如图所示,P为平分线上的点,于D,,则点P到OB的距离为( )
A.5cm B.4cm C.3cm D.2cm
6、有两边相等的三角形的两边长为,,则它的周长为( )
A. B. C. D.或
7、等腰三角形的顶角是,则这个三角形的一个底角的大小是( )
A. B. C. D.
8、一副三角板如图放置,点A在DF的延长线上,∠D=∠BAC=90°,∠E=30°,∠C=45°,若BC//DA,则∠ABF的度数为( )
A.15° B.20° C.25° D.30°
二、填空题(共 6 小题)
1、如图,四边形中,,连接,平分,E是直线上一点,,,则的长为________.
2、如图,△ABC中,AB平分∠DAC,AB⊥BC,垂足为B,若∠ADC与∠ACB互补,BC=5,则CD的长为_________.
3、如图,在四边形ABCE中,∠B=∠A,∠E=90°,点D在AB上,AD∶BD=5∶11,连接CD,若点D在CE的垂直平分线上且满足∠A=2∠BDC,CE=10,则线段AB的长为______.
4、如图,AD⊥BC,∠1=∠B,∠C=65°,∠BAC=__________
5、如图,在中,AD是的平分线,,,则____________.
6、如图所示,直线与两坐标轴分别交于、两点,点是的中点,、分别是直线、轴上的动点,当周长最小时,点的坐标为_____.
三、解答题(共 5 小题)
1、如图,在中,,,.
(1)的面积等于_______;
(2)为线段上一点,过点作,垂足为.当时,请在如图所示的矩形区域内,用无刻度的直尺和圆规,画出线段,并简要说明点和点的位置是如何找到的(保留作图痕迹,不要求证明).
2、如图,是等边三角形,,分别交AB,AC于点D,E.
(1)求证:是等边三角形;
(2)点F在线段DE上,点G在外,,,求证:.
3、2021年10月10日是辛亥革命110周年纪念日.为进一步弘扬辛亥革命中体现的中华民族的伟大革命精神,社区开展了系列纪念活动.如图,有一块四边形空地,社区计划将其布置成展区,陈列有关辛亥革命的历史图片.现测得,,,且.
(1)试说明;
(2)求四边形展区(阴影部分)的面积.
4、设两个点A、B的坐标分别为,,则线段AB的长度为:.举例如下:A、B两点的坐标是,,则A、B两点之间的距离.请利用上述知识解决下列问题:
(1)若,,且,求x的值;
(2)已知△ABC,点A为、点B为、点C为,求△ABC的面积;
(3)求代数式的最小值.
5、如图,在△ABC中,AC=BC,∠ACB=90°,点D是边AB上的动点,连接CD,点B关于直线CD的对称点为点E,射线AE与射线CD交于点F.
(1)在图中,依题意补全图形;
(2)记∠DCB=α(α<45°),求∠BAF的大小;(用含α的式子表示)
(3)若△BCE是等边三角形,猜想EF和AB的数量关系,并证明你的结论.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
