新教材必修一5.7三角函数的应用(第1课时)(共16张PPT)
文档属性
| 名称 | 新教材必修一5.7三角函数的应用(第1课时)(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 757.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 16:47:13 | ||
图片预览






文档简介
(共16张PPT)
学习目标 学科素养
1.掌握三角函数模型应用基本步骤. 2.选择合理三角函数模型解决实际问题,注意在复杂的背景中抽取基本的数学关系,还要调动相关学科知识来理解问题。 3.感受数学建模的全过程,体验数学在解决实际问题中的价值和作用及数学和日常生活和其它学科的联系。 1.数学抽象:将实际问题转化为三角函数问题;2.逻辑推理:运用三角函数解决问题;
3.直观想象:由图像求函数关系式;
4.数学运算:三角函数的恒等变换;
5.数据分析:有采集的数据分析获得函数模型
6.数学建模:由实际问题建立对应的函数模型.
5.7 三角函数的应用(1)
提出问题
现实生活中存在大量具有周而复始、循环往复特点的周期运动变化现象,如果某种变化着的现象具有周期性,那么就可以考虑借助三角函数来描述.
本节通过几个具体实例,说明三角函数模型的简单应用.
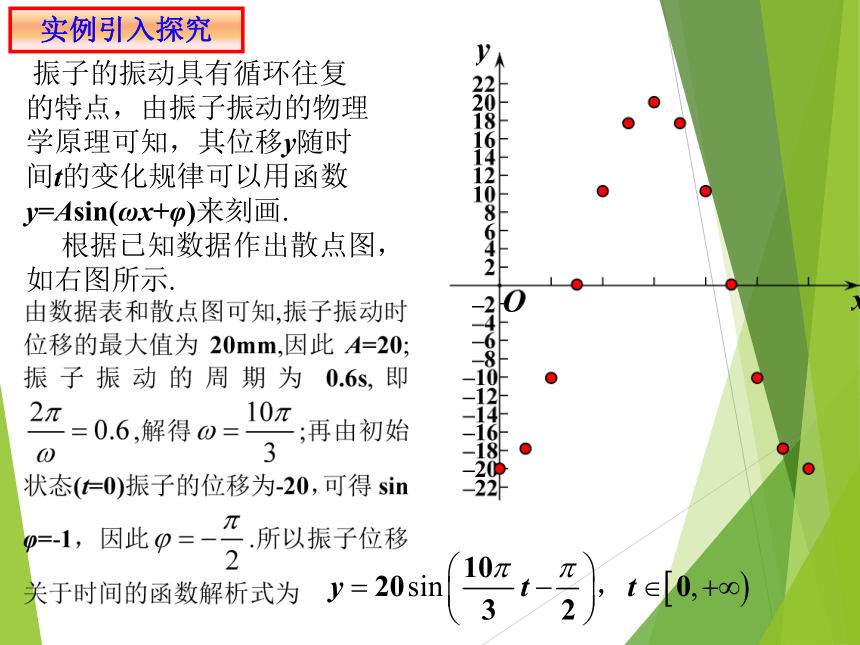
实例引入探究
问题1:某个弹簧振子(简称振子)在完成一次全振动的过程中,时间t(单位:s)与位移y(单位:mm)之间的对应数据如表所示。试根据这些数据确定这个振子的位移关于时间的函数解析式。
t 0.00 0.05 0.10 0.15 0.20 0.25 0.30
y -20.0 -17.8 -10.1 0.1 10.3 17.7 20.0
t 0.35 0.40 0.45 0.50 0.55 0.60
y 17.7 10.3 0.1 -10.1 -17.8 -20.0
实例引入探究
振子的振动具有循环往复的特点,由振子振动的物理学原理可知,其位移y随时间t的变化规律可以用函数y=Asin(ωx+φ)来刻画.
根据已知数据作出散点图,如右图所示.
新知探究
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动等等。这些都是物体在某一中心位置附近循环往复的运动.
A:这个量振动时离开平衡位置
的最大距离,称为“振幅”.
函数表示一个振动量时:
T:
f :
称为“相位” .
x=0时的相位,称为“初相”.
:
应用探究
问题2:图(1)是某次实验测得的交变电流i(单位:A)随时间t(单位:s)变化的图象(频率为50HZ)。将测得的图象放大,得到图2
(1)求电流i随时间t变化的函数解析式;
(2)当 时,求电流i
(1)
(2)
解:由交变电流的产生原理可知,电流 i 随时间 t 的变化规律可用i=Asin(ωt+φ)来刻画,其中 表示频率,A表示振幅,φ表示初相.
再由初始状态(t=0)的电流为4.33A,可得
sin φ=0.866,因此φ约为
所以电流随时间变化的函数解析式是
电流变化的周期为 s,频率为50Hz,即 ,解得ω=100π;
由图可知,电流最大值为5A,因此A=5;
应用探究
(1)
所以
(2)转动5分钟后距地面高度为37.5米.
巩固新知
例3.如右图,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色,若摩天轮最高点距地面高度为120米,转盘直径为110米,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到离地面最近的位置进仓,转一周大约需要30分钟。
(1)游客坐上摩天轮的座舱,开始转动t分钟后离地面的高度为H米,求在转动一周的过程中,H关于t的函数解析式。
(2)求游客甲在开始转动5分钟后距离地面的高度。
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差的最大值(精确到0.1)
(3)甲、乙两人的位置分别用A,B表示,如图所示,则 .经过t分钟后甲距离地面的高度为
,点B相对于点A始终落后 ,
所以经过t分钟后乙距离地面的高度为
则甲、乙距离地面的高度差为
应用和差化积公式可得
当 ,即 或22.8时,h的最大值
米.
巩固新知
巩固新知
如图,摩天轮的半径为40米,其中心O点距离地面的高度为50米,摩天轮按逆时针方向匀速转动,且20分钟转一圈,若摩天轮上点P的起始位置在最高点处,则摩天轮转动过程中( )
A.经过10分钟后点P距离地面10米
B.若摩天轮转速减半,则其周期变为原来的
C.第17分钟和第43分钟时点P距离地面的
高度相同
D.摩天轮转动一圈,点P距离地面的高度不低
于70米的时间为 分钟
点P到地面的距离为
变式应用
(1)由最低点到达最高点是半圈,耗时10分钟
(2)设该盛水筒距离水面的高度为y,可得
令
即
所以
解得
所以转动一周的过程中,水流出的时间为 分钟
拓展学习
例1.某筒车半径为10米,筒车转轮中心距离水面的高度为6米,筒车逆时针匀速转动,每20分钟转一圈,某个盛水筒开始时位于最低点,则
(1)这个盛水筒经过几分钟第一次到达最高点?
(2)当盛水筒距离水面高度不低于11米时,其中的水会流出,则在转动一周的过程中,水流出的时间是多少?
备选例题
1.解三角函数应用题的基本步骤:
(1)审清题意;
(2)搜集整理数据,建立数学模型;
(3)讨论变量关系,求解数学模型;
(4)检验,作出结论
总结反思 升华素养
2.根据三角函数图象建立函数解析式,就是要抓住图象的数字特征确定相关的参数值,同时要注意函数的定义域.
课后作业
1.P241T6,T7;P248练习T1;
2.P249习题5.7T2,P256T25
学习目标 学科素养
1.掌握三角函数模型应用基本步骤. 2.选择合理三角函数模型解决实际问题,注意在复杂的背景中抽取基本的数学关系,还要调动相关学科知识来理解问题。 3.感受数学建模的全过程,体验数学在解决实际问题中的价值和作用及数学和日常生活和其它学科的联系。 1.数学抽象:将实际问题转化为三角函数问题;2.逻辑推理:运用三角函数解决问题;
3.直观想象:由图像求函数关系式;
4.数学运算:三角函数的恒等变换;
5.数据分析:有采集的数据分析获得函数模型
6.数学建模:由实际问题建立对应的函数模型.
5.7 三角函数的应用(1)
提出问题
现实生活中存在大量具有周而复始、循环往复特点的周期运动变化现象,如果某种变化着的现象具有周期性,那么就可以考虑借助三角函数来描述.
本节通过几个具体实例,说明三角函数模型的简单应用.
实例引入探究
问题1:某个弹簧振子(简称振子)在完成一次全振动的过程中,时间t(单位:s)与位移y(单位:mm)之间的对应数据如表所示。试根据这些数据确定这个振子的位移关于时间的函数解析式。
t 0.00 0.05 0.10 0.15 0.20 0.25 0.30
y -20.0 -17.8 -10.1 0.1 10.3 17.7 20.0
t 0.35 0.40 0.45 0.50 0.55 0.60
y 17.7 10.3 0.1 -10.1 -17.8 -20.0
实例引入探究
振子的振动具有循环往复的特点,由振子振动的物理学原理可知,其位移y随时间t的变化规律可以用函数y=Asin(ωx+φ)来刻画.
根据已知数据作出散点图,如右图所示.
新知探究
现实生活中存在大量类似弹簧振子的运动,如钟摆的摆动,水中浮标的上下浮动,琴弦的振动等等。这些都是物体在某一中心位置附近循环往复的运动.
A:这个量振动时离开平衡位置
的最大距离,称为“振幅”.
函数表示一个振动量时:
T:
f :
称为“相位” .
x=0时的相位,称为“初相”.
:
应用探究
问题2:图(1)是某次实验测得的交变电流i(单位:A)随时间t(单位:s)变化的图象(频率为50HZ)。将测得的图象放大,得到图2
(1)求电流i随时间t变化的函数解析式;
(2)当 时,求电流i
(1)
(2)
解:由交变电流的产生原理可知,电流 i 随时间 t 的变化规律可用i=Asin(ωt+φ)来刻画,其中 表示频率,A表示振幅,φ表示初相.
再由初始状态(t=0)的电流为4.33A,可得
sin φ=0.866,因此φ约为
所以电流随时间变化的函数解析式是
电流变化的周期为 s,频率为50Hz,即 ,解得ω=100π;
由图可知,电流最大值为5A,因此A=5;
应用探究
(1)
所以
(2)转动5分钟后距地面高度为37.5米.
巩固新知
例3.如右图,摩天轮是一种大型转轮状的机械建筑设施,游客坐在摩天轮的座舱里慢慢地往上转,可以从高处俯瞰四周景色,若摩天轮最高点距地面高度为120米,转盘直径为110米,设置有48个座舱,开启后按逆时针方向匀速旋转,游客在座舱转到离地面最近的位置进仓,转一周大约需要30分钟。
(1)游客坐上摩天轮的座舱,开始转动t分钟后离地面的高度为H米,求在转动一周的过程中,H关于t的函数解析式。
(2)求游客甲在开始转动5分钟后距离地面的高度。
(3)若甲、乙两人分别坐在两个相邻的座舱里,在运行一周的过程中,求两人距离地面的高度差的最大值(精确到0.1)
(3)甲、乙两人的位置分别用A,B表示,如图所示,则 .经过t分钟后甲距离地面的高度为
,点B相对于点A始终落后 ,
所以经过t分钟后乙距离地面的高度为
则甲、乙距离地面的高度差为
应用和差化积公式可得
当 ,即 或22.8时,h的最大值
米.
巩固新知
巩固新知
如图,摩天轮的半径为40米,其中心O点距离地面的高度为50米,摩天轮按逆时针方向匀速转动,且20分钟转一圈,若摩天轮上点P的起始位置在最高点处,则摩天轮转动过程中( )
A.经过10分钟后点P距离地面10米
B.若摩天轮转速减半,则其周期变为原来的
C.第17分钟和第43分钟时点P距离地面的
高度相同
D.摩天轮转动一圈,点P距离地面的高度不低
于70米的时间为 分钟
点P到地面的距离为
变式应用
(1)由最低点到达最高点是半圈,耗时10分钟
(2)设该盛水筒距离水面的高度为y,可得
令
即
所以
解得
所以转动一周的过程中,水流出的时间为 分钟
拓展学习
例1.某筒车半径为10米,筒车转轮中心距离水面的高度为6米,筒车逆时针匀速转动,每20分钟转一圈,某个盛水筒开始时位于最低点,则
(1)这个盛水筒经过几分钟第一次到达最高点?
(2)当盛水筒距离水面高度不低于11米时,其中的水会流出,则在转动一周的过程中,水流出的时间是多少?
备选例题
1.解三角函数应用题的基本步骤:
(1)审清题意;
(2)搜集整理数据,建立数学模型;
(3)讨论变量关系,求解数学模型;
(4)检验,作出结论
总结反思 升华素养
2.根据三角函数图象建立函数解析式,就是要抓住图象的数字特征确定相关的参数值,同时要注意函数的定义域.
课后作业
1.P241T6,T7;P248练习T1;
2.P249习题5.7T2,P256T25
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
