列一元二次方程解应用题
图片预览





文档简介
课件25张PPT。列一元二次方程解应用题活动中体验◆竹竿竖比城门高3尺,横比城门宽6尺,沿着城门的两个对角斜着拿,刚好进去,如果城门是长方形的,你知道竹竿有多长吗?解:设竹竿长为x尺,则城门高为( x -3)尺,宽为( x -6)尺.x -6由勾股定理得:
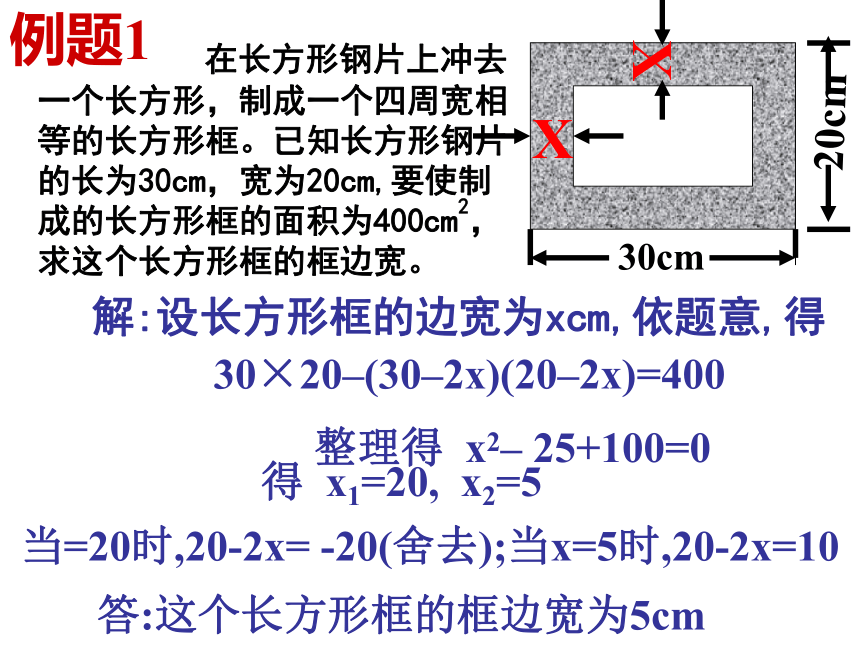
( x –3)2+(x –6)2= x 2即 x 2 -18 x +45 = 0x -3x 活动中体验实际问题 数学问题 方程模型 在长方形钢片上冲去一个长方形,制成一个四周宽相等的长方形框。已知长方形钢片的长为30cm,宽为20cm,要使制成的长方形框的面积为400cm2,求这个长方形框的框边宽。
解:设长方形框的边宽为xcm,依题意,得30×20–(30–2x)(20–2x)=400整理得 x2– 25+100=0得 x1=20, x2=5当=20时,20-2x= -20(舍去);当x=5时,20-2x=10答:这个长方形框的框边宽为5cm例题1 列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?
2.设:设未知数,语句要完整,
有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,
注明单位且要贴近生活.
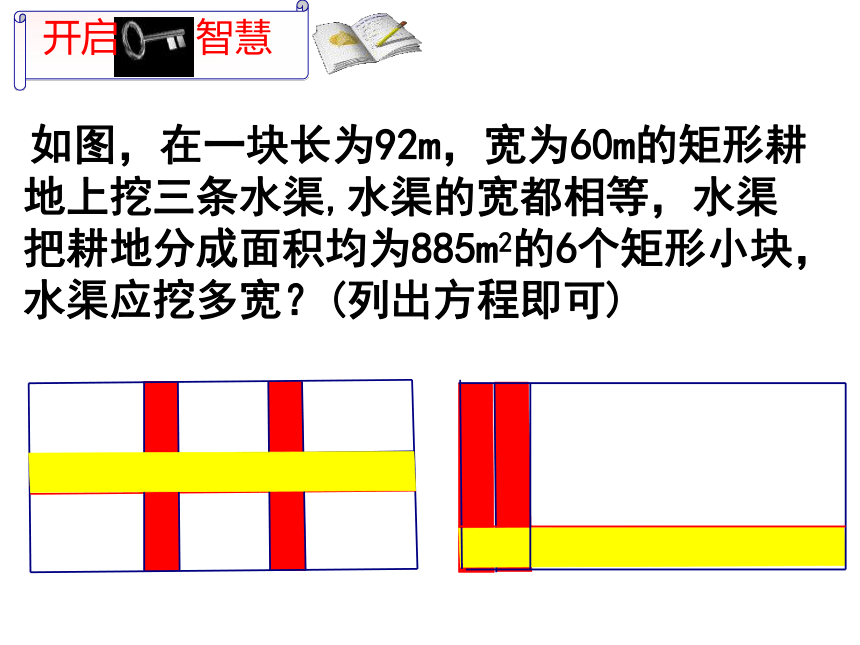
列方程解应用题的关键是:找出相等关系. 如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽?(列出方程即可)
例题2 如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽?(列出方程即可)
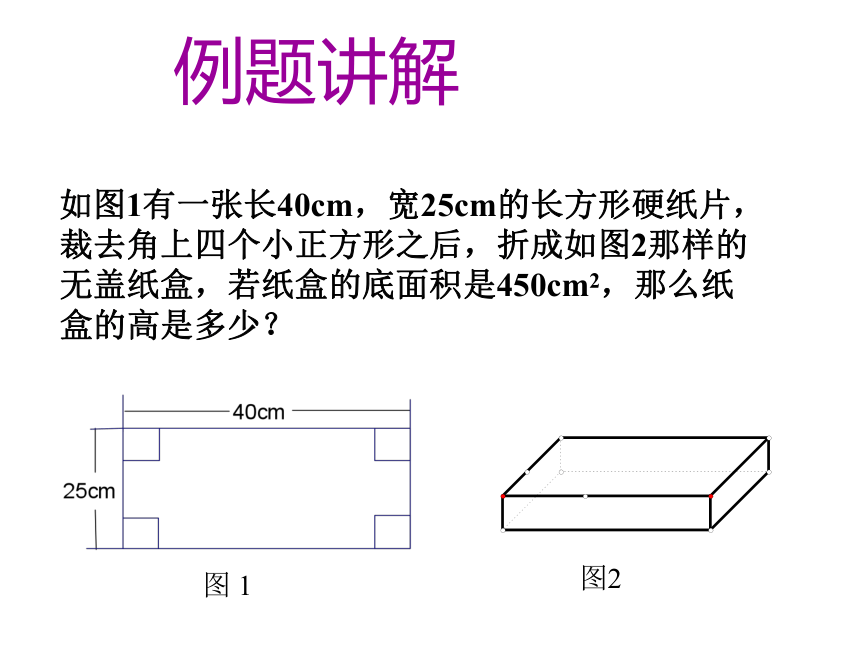
如图1有一张长40cm,宽25cm的长方形硬纸片,
裁去角上四个小正方形之后,折成如图2那样的
无盖纸盒,若纸盒的底面积是450cm2,那么纸
盒的高是多少? 例题讲解图 1图2(2)底面的长和宽能否用含x的代数式表示? (3)你能找出题中的等量关系吗?你怎样列方程?
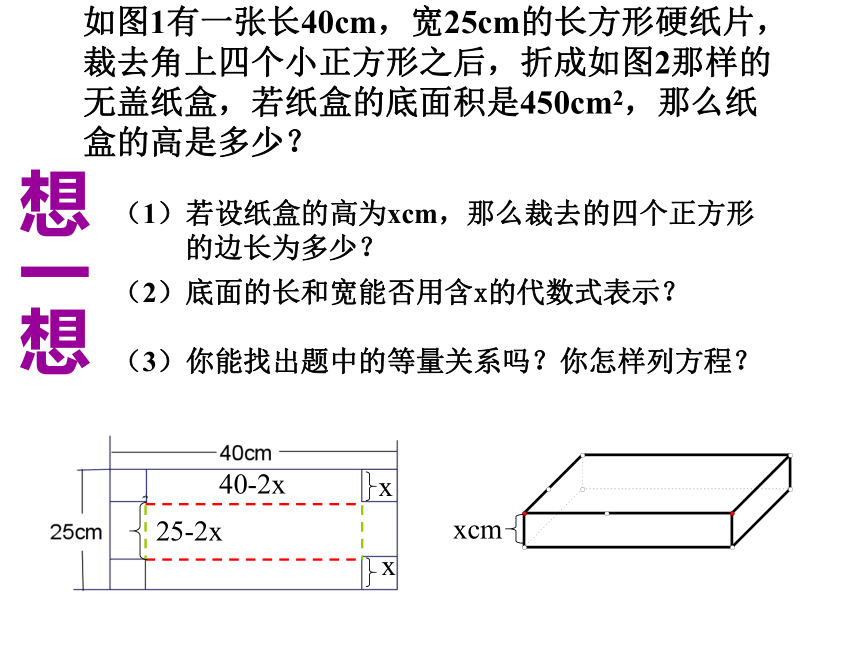
(1)若设纸盒的高为xcm,那么裁去的四个正方形
的边长为多少?想一想 如图1有一张长40cm,宽25cm的长方形硬纸片,
裁去角上四个小正方形之后,折成如图2那样的
无盖纸盒,若纸盒的底面积是450cm2,那么纸
盒的高是多少? 40-2x例2、某工厂一月份的产值是5万元, 三月份的产值是7.2万元, 求月平均增长率是多少?
解:设月平均增长率为X,依题意,得
5(1+X)2=7.2
(1+X)2=1.44
1+X=±1.2
所以X1=0.2,X2=-2.2
答:月平均增长率为20%.由于增长率不可能为负.所以X2=-2.2不符合题意,舍去.因此符合本题的X为 X=0.2=20% 例3. 北京市政府为迎接2008年奥运会,决定改善城市容貌,绿化环境,计划经过两年时间,将城市绿地面积增加44 %,求这两年平均每年绿地面积增长率03年的数量为A,05年的数量为B,经过两个时间单位,求平均增长率x。某季度数量为B,头一个月数量为A,求后两个月的增长率x.
03年的数量A,经过两个时间单位后数量增加m%,求平均增长率x.比较增加m%==A+A(1+x)+A(1+x)2=B?
1、党的十六大提出全面建设小康社会,加快推进社会主义现代化建设,力争国民生产总值到2020年比2000年翻两番,在本世纪的头二十年(2001年至2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的平均增长率为x,那么x满足的方程为_____________ 相信自己(1+x)2=4?
?
?
2、某经济开发区今年一月份工业产值达50亿元,第一季度总产值达175亿元,问二、三月份平均每月的增长率为多少?设平均每月增长率为x,根据题意得方程:________________________
相信自己50+50(1+x)+50(1+x) 2=175①根据图中所提供的信息回答下列问题:2003年底的绿地面积为 公顷,比2002年底增加了 公顷;在2001年,2002年,2003年这三个中,绿地面积最多的是_______年;
②为满足城市发展的需要,计划到
2005年底使城区绿地面积达到72.6
公顷,试求今明两年绿地面积的
年平均增长率。
?
?
3、美化城市,改善人们的居住环境已成为城市建设的一项重要内容。我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示)。
相信自己6042003如图,斜靠在墙上的一根竹竿长AB=6.5m,BC=2.5m,若A端沿垂直于地面的方向AC下滑1m,问B端将沿CB方向移动多少m?ABCA’B’相信自己 练习.某种药剂原售价为4元, 经过两次降价, 现在每瓶售价为2.56元,问平均每次降价百分之几? 相信自己 幻灯片 14例4 新亚商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?驶向胜利的彼岸有关利润的知识基本知识商品利润=售价-进价;我是商场经理例2 新华商场销售某种冰箱,每台进价为250元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?我是商场经理例2 新华商场销售某种冰箱,每台进价为250元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?我是商场精英1. 某种服装,平均每天可销售20件,每件盈利44元.若每件降价1元,则每天可多售5件.如果每天盈利1600元,每应降价多少元?回味无穷列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,注明单位且要贴近生活.
列方程解应用题的关键是: 找出相等关系.
关于两次平均增长(降低)率问题的一般关系:
A(1±x)2=B(其中A表示基数,x表表示增长(或降低)率,B表示新数)思考:如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s,的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?结束寄语一元二次方程也是刻画现实世界的有效数学模型.
用列方程的方法去解释或解答一些生活中的现象或问题是一种重要的数学方程方法——即方程的思想.
( x –3)2+(x –6)2= x 2即 x 2 -18 x +45 = 0x -3x 活动中体验实际问题 数学问题 方程模型 在长方形钢片上冲去一个长方形,制成一个四周宽相等的长方形框。已知长方形钢片的长为30cm,宽为20cm,要使制成的长方形框的面积为400cm2,求这个长方形框的框边宽。
解:设长方形框的边宽为xcm,依题意,得30×20–(30–2x)(20–2x)=400整理得 x2– 25+100=0得 x1=20, x2=5当=20时,20-2x= -20(舍去);当x=5时,20-2x=10答:这个长方形框的框边宽为5cm例题1 列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?
2.设:设未知数,语句要完整,
有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,
注明单位且要贴近生活.
列方程解应用题的关键是:找出相等关系. 如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽?(列出方程即可)
例题2 如图,在一块长为92m,宽为60m的矩形耕地上挖三条水渠,水渠的宽都相等,水渠把耕地分成面积均为885m2的6个矩形小块,水渠应挖多宽?(列出方程即可)
如图1有一张长40cm,宽25cm的长方形硬纸片,
裁去角上四个小正方形之后,折成如图2那样的
无盖纸盒,若纸盒的底面积是450cm2,那么纸
盒的高是多少? 例题讲解图 1图2(2)底面的长和宽能否用含x的代数式表示? (3)你能找出题中的等量关系吗?你怎样列方程?
(1)若设纸盒的高为xcm,那么裁去的四个正方形
的边长为多少?想一想 如图1有一张长40cm,宽25cm的长方形硬纸片,
裁去角上四个小正方形之后,折成如图2那样的
无盖纸盒,若纸盒的底面积是450cm2,那么纸
盒的高是多少? 40-2x例2、某工厂一月份的产值是5万元, 三月份的产值是7.2万元, 求月平均增长率是多少?
解:设月平均增长率为X,依题意,得
5(1+X)2=7.2
(1+X)2=1.44
1+X=±1.2
所以X1=0.2,X2=-2.2
答:月平均增长率为20%.由于增长率不可能为负.所以X2=-2.2不符合题意,舍去.因此符合本题的X为 X=0.2=20% 例3. 北京市政府为迎接2008年奥运会,决定改善城市容貌,绿化环境,计划经过两年时间,将城市绿地面积增加44 %,求这两年平均每年绿地面积增长率03年的数量为A,05年的数量为B,经过两个时间单位,求平均增长率x。某季度数量为B,头一个月数量为A,求后两个月的增长率x.
03年的数量A,经过两个时间单位后数量增加m%,求平均增长率x.比较增加m%==A+A(1+x)+A(1+x)2=B?
1、党的十六大提出全面建设小康社会,加快推进社会主义现代化建设,力争国民生产总值到2020年比2000年翻两番,在本世纪的头二十年(2001年至2020年),要实现这一目标,以十年为单位计算,设每个十年的国民生产总值的平均增长率为x,那么x满足的方程为_____________ 相信自己(1+x)2=4?
?
?
2、某经济开发区今年一月份工业产值达50亿元,第一季度总产值达175亿元,问二、三月份平均每月的增长率为多少?设平均每月增长率为x,根据题意得方程:________________________
相信自己50+50(1+x)+50(1+x) 2=175①根据图中所提供的信息回答下列问题:2003年底的绿地面积为 公顷,比2002年底增加了 公顷;在2001年,2002年,2003年这三个中,绿地面积最多的是_______年;
②为满足城市发展的需要,计划到
2005年底使城区绿地面积达到72.6
公顷,试求今明两年绿地面积的
年平均增长率。
?
?
3、美化城市,改善人们的居住环境已成为城市建设的一项重要内容。我市近几年来,通过拆迁旧房,植草,栽树,修公园等措施,使城区绿地面积不断增加(如图所示)。
相信自己6042003如图,斜靠在墙上的一根竹竿长AB=6.5m,BC=2.5m,若A端沿垂直于地面的方向AC下滑1m,问B端将沿CB方向移动多少m?ABCA’B’相信自己 练习.某种药剂原售价为4元, 经过两次降价, 现在每瓶售价为2.56元,问平均每次降价百分之几? 相信自己 幻灯片 14例4 新亚商场销售某种冰箱,每台进价为2500元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?驶向胜利的彼岸有关利润的知识基本知识商品利润=售价-进价;我是商场经理例2 新华商场销售某种冰箱,每台进价为250元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?我是商场经理例2 新华商场销售某种冰箱,每台进价为250元.市场调研表明:当销售价为2900元时,平均每天能售出8台;而当销价每降低50元时,平均每天能多售4台.商场要想使这种冰箱的销售利润平均每天达到5000元,每台冰箱的定价应为多少元?我是商场精英1. 某种服装,平均每天可销售20件,每件盈利44元.若每件降价1元,则每天可多售5件.如果每天盈利1600元,每应降价多少元?回味无穷列方程解应用题的一般步骤是:
1.审:审清题意:已知什么,求什么?
2.设:设未知数,语句要完整,有单位(同一)的要注明单位;
3.列:列代数式,找出相等关系列方程;
4.解:解所列的方程;
5.验:是否是所列方程的根;是否符合题意;
6.答:答案也必需是完整的语句,注明单位且要贴近生活.
列方程解应用题的关键是: 找出相等关系.
关于两次平均增长(降低)率问题的一般关系:
A(1±x)2=B(其中A表示基数,x表表示增长(或降低)率,B表示新数)思考:如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC向点C以2cm/s,的速度移动,如果P、Q分别从A、B同时出发,那么几秒后五边形APQCD的面积为64cm2?结束寄语一元二次方程也是刻画现实世界的有效数学模型.
用列方程的方法去解释或解答一些生活中的现象或问题是一种重要的数学方程方法——即方程的思想.
