一元二次方程
图片预览






文档简介
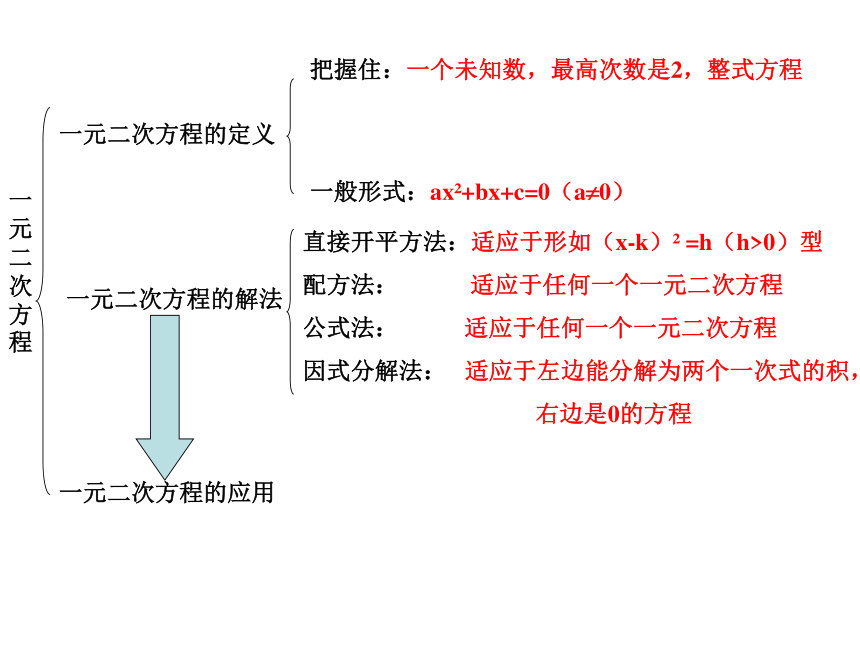
课件16张PPT。一元二次方程复习课 通过复习,掌握一元二次方程的概念,并能够熟练的解一元二次方程,并且利用一元二次方程解决实际问题一元二次方程一元二次方程的定义一元二次方程的解法一元二次方程的应用把握住:一个未知数,最高次数是2,整式方程一般形式:ax2+bx+c=0(a?0)直接开平方法:适应于形如(x-k)2 =h(h>0)型
配方法: 适应于任何一个一元二次方程
公式法: 适应于任何一个一元二次方程
因式分解法: 适应于左边能分解为两个一次式的积,
右边是0的方程一、一元二次方程的概念
引例:判断下列方程是不是一元二次方程
(1)4x- x2 + =0 (2)3x2 - y -1=0
(3)ax2 +bx+c=0 (4)x + =0注意:一元二次方程的 三个要素巩固提高:
1、已知关于x的方程(m2-1)x2+(m-1)x-2m+1=0,当m
时是一元二次方程,当m= 时是一元一次方程,
当m= 时,x=0。
2、若(m+2)x 2 +(m-2) x -2=0是关于x的一元二次方程则m 。是不是不是≠±1 ≠- 2±1?不一定二、一元二次方程的解法你还记得吗?请你选择最恰当的方法解下列一元二次方程
1、3x2 -1=0 2、x(2x +3)=5(2x +3)
3、x2 - 3 x +2=0 4、2 x 2 -5x+1=0点评:1、形如(x-k)2=h的方程可以用直接开平方法求解
2、千万记住:方程的两边有相同的含有未知数的因式的时候不能两边都除以这个因式,因为这样能把方程的一个跟丢失了,要利用因式分解法求解。
3、当方程的左边是二次三项式的时候优先用十字相乘法求解。
当我们不能利用上边的方法求解的时候就就可以用公式法求解,公式法是万能的。
练习:用最好的方法求解下列方程
1、(3x -2)2-49=0 2、(3x -4)2=(4x -3)2 3、4y = 1 - y2解: (3x-2)2=49
3x -2=±7
x=
x1=3,x2= -解:
法一3x-4=±(4x-3)
?3x -4=4x-3或3x-4=-4x+3
?-x=1或 7x=7
? x1 = -1, x2 =1
法二(3x-4)2 -(4x-3)2 =0(3x-4+4x-3)(3x-4x+3)=0
(7x-7)(-x-1)=0
7x-7=0或-x-1=0
? x1 = -1, x2 =1
解:3y2+8y -2=0
b2 - 4ac
=64 -4?3?(-2)
=88
X=
检查你的复习效果:1、用配方法解方程2x2 +4x +1 =0,配方后得到的方程是 。
2、一元二次方程ax2 +bx +c =0,
若x=1是它的一个根,则a+b+c= ,
若a -b+c=0,则方程必有一根为 。
3、4、方程2 x 2-mx-m2 =0有一个根为 - 1, 则m= ,另一个根为 。2(x+1)2=105或-1。2或-12或1/2-1阅读材料,解答问题 为了解方程(y2-1)2 -3(y2-1)+2=0,我们将y2-1视为一个整体,解:设 y2-1=a,则(y2-1)2=a2,
a2 - 3a+2=0, (1)
a1=1,a2=2。
当a=1时,y2 -1=1,y =± ,
当a=2时,y2-1=2,y=±
所以y1= ,y2 =- y 3= y4= -解答问题:1、在由原方程得到方程(1)的过程中,利用了 , 法达到了降次的目的,体现了 的数学思想。
2、用上述方法解下列方程: 一元二次方程根的判别式两不相等实根两相等实根无实根一元二次方程一元二次方程 根的判式是: 判别式的情况根的情况定理与逆定理两个不相等实根 两个相等实根 无实根(无解)三、判别式的应用:所以,原方程有两个不相等的实根。说明:解这类题目时,一般要先把方程化为一般形式,求出△,然后对△进行计算,使△的符号明朗化,进而说明△的符号情况,得出结论。1、不解方程,判别方程的根的情况 例2:当k取什么值时,已知关于x的方程:
(1)方程有两个不相等的实根;(2)方程有两个相等的实根;(3)方程无实根;
解:△=(1).当△>0 ,方程有两个不相等的实根, 8k+9 >0 , 即 (2).当△ = 0 ,方程有两个相等的实根, 8k+9 =0 , 即 (3).当△ <0 ,方程有没有实数根, 8k+9 <0 , 即 2、根据方程的根的情况确定方程的待定系数的取值范围 说明:解此类题目时,也是先把方程化为一般形式,再算出△,再由题目给出的根的情况确定△的情况。从而求出待定系数的取值范围K<例3、已知m为非负整数,且关于x的方程 :
有两个实数根,求m的值。 解:∵方程有两个实数根
∴
解得:∵m为非负数∴m=0或m=1说明:当二次项系数也含有待定的字母时,要注意二次项系数不能为0,还要注意题目中待定字母的取值范围.例4、求证:关于x的方程:
有两个不相等的实根。证明: 所以,无论m取任何实数,方程有两个不相等的实数根。无论m取任何实数都有:即:△>03、证明方程根的情况说明:此类题目要先把方程化成一般形式,再计算出△,如果不能直接判断△情况,就利用配方法把△配成含用完全平方的形式,根据完全平方的非负性,判断△的情况,从而证明出方程根的情况.2、已知关于x 的方程: 有两个
不相等的实数根,k为实数,求k 的取值范围。3、设关于x 的方程: ,证明,不论m
为何 值时,方程总有两个不相等的实数根。例题讲解例1 把分解因式此步的目的是去掉括号内的分母解:设方程的另一个根为x1,那么用配方法证明:关于x的方程(m2 -12m +37)x 2 +3mx+1=0, 无论m取何值,此方程都是一元二次方程
配方法: 适应于任何一个一元二次方程
公式法: 适应于任何一个一元二次方程
因式分解法: 适应于左边能分解为两个一次式的积,
右边是0的方程一、一元二次方程的概念
引例:判断下列方程是不是一元二次方程
(1)4x- x2 + =0 (2)3x2 - y -1=0
(3)ax2 +bx+c=0 (4)x + =0注意:一元二次方程的 三个要素巩固提高:
1、已知关于x的方程(m2-1)x2+(m-1)x-2m+1=0,当m
时是一元二次方程,当m= 时是一元一次方程,
当m= 时,x=0。
2、若(m+2)x 2 +(m-2) x -2=0是关于x的一元二次方程则m 。是不是不是≠±1 ≠- 2±1?不一定二、一元二次方程的解法你还记得吗?请你选择最恰当的方法解下列一元二次方程
1、3x2 -1=0 2、x(2x +3)=5(2x +3)
3、x2 - 3 x +2=0 4、2 x 2 -5x+1=0点评:1、形如(x-k)2=h的方程可以用直接开平方法求解
2、千万记住:方程的两边有相同的含有未知数的因式的时候不能两边都除以这个因式,因为这样能把方程的一个跟丢失了,要利用因式分解法求解。
3、当方程的左边是二次三项式的时候优先用十字相乘法求解。
当我们不能利用上边的方法求解的时候就就可以用公式法求解,公式法是万能的。
练习:用最好的方法求解下列方程
1、(3x -2)2-49=0 2、(3x -4)2=(4x -3)2 3、4y = 1 - y2解: (3x-2)2=49
3x -2=±7
x=
x1=3,x2= -解:
法一3x-4=±(4x-3)
?3x -4=4x-3或3x-4=-4x+3
?-x=1或 7x=7
? x1 = -1, x2 =1
法二(3x-4)2 -(4x-3)2 =0(3x-4+4x-3)(3x-4x+3)=0
(7x-7)(-x-1)=0
7x-7=0或-x-1=0
? x1 = -1, x2 =1
解:3y2+8y -2=0
b2 - 4ac
=64 -4?3?(-2)
=88
X=
检查你的复习效果:1、用配方法解方程2x2 +4x +1 =0,配方后得到的方程是 。
2、一元二次方程ax2 +bx +c =0,
若x=1是它的一个根,则a+b+c= ,
若a -b+c=0,则方程必有一根为 。
3、4、方程2 x 2-mx-m2 =0有一个根为 - 1, 则m= ,另一个根为 。2(x+1)2=105或-1。2或-12或1/2-1阅读材料,解答问题 为了解方程(y2-1)2 -3(y2-1)+2=0,我们将y2-1视为一个整体,解:设 y2-1=a,则(y2-1)2=a2,
a2 - 3a+2=0, (1)
a1=1,a2=2。
当a=1时,y2 -1=1,y =± ,
当a=2时,y2-1=2,y=±
所以y1= ,y2 =- y 3= y4= -解答问题:1、在由原方程得到方程(1)的过程中,利用了 , 法达到了降次的目的,体现了 的数学思想。
2、用上述方法解下列方程: 一元二次方程根的判别式两不相等实根两相等实根无实根一元二次方程一元二次方程 根的判式是: 判别式的情况根的情况定理与逆定理两个不相等实根 两个相等实根 无实根(无解)三、判别式的应用:所以,原方程有两个不相等的实根。说明:解这类题目时,一般要先把方程化为一般形式,求出△,然后对△进行计算,使△的符号明朗化,进而说明△的符号情况,得出结论。1、不解方程,判别方程的根的情况 例2:当k取什么值时,已知关于x的方程:
(1)方程有两个不相等的实根;(2)方程有两个相等的实根;(3)方程无实根;
解:△=(1).当△>0 ,方程有两个不相等的实根, 8k+9 >0 , 即 (2).当△ = 0 ,方程有两个相等的实根, 8k+9 =0 , 即 (3).当△ <0 ,方程有没有实数根, 8k+9 <0 , 即 2、根据方程的根的情况确定方程的待定系数的取值范围 说明:解此类题目时,也是先把方程化为一般形式,再算出△,再由题目给出的根的情况确定△的情况。从而求出待定系数的取值范围K<例3、已知m为非负整数,且关于x的方程 :
有两个实数根,求m的值。 解:∵方程有两个实数根
∴
解得:∵m为非负数∴m=0或m=1说明:当二次项系数也含有待定的字母时,要注意二次项系数不能为0,还要注意题目中待定字母的取值范围.例4、求证:关于x的方程:
有两个不相等的实根。证明: 所以,无论m取任何实数,方程有两个不相等的实数根。无论m取任何实数都有:即:△>03、证明方程根的情况说明:此类题目要先把方程化成一般形式,再计算出△,如果不能直接判断△情况,就利用配方法把△配成含用完全平方的形式,根据完全平方的非负性,判断△的情况,从而证明出方程根的情况.2、已知关于x 的方程: 有两个
不相等的实数根,k为实数,求k 的取值范围。3、设关于x 的方程: ,证明,不论m
为何 值时,方程总有两个不相等的实数根。例题讲解例1 把分解因式此步的目的是去掉括号内的分母解:设方程的另一个根为x1,那么用配方法证明:关于x的方程(m2 -12m +37)x 2 +3mx+1=0, 无论m取何值,此方程都是一元二次方程
