2022-2023学年数学人教版九年级下册第二十八章 锐角三角函数 同步练 (含解析)
文档属性
| 名称 | 2022-2023学年数学人教版九年级下册第二十八章 锐角三角函数 同步练 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 857.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 20:59:37 | ||
图片预览




文档简介
第二十八章 锐角三角函数
一、单选题
1.已知,则锐角α的度数是( )
A.60° B.45° C.30° D.75°
2.在Rt△ACB中,∠C=90°,AB=8,sinA=,则BC的长为( )
A.6 B.7.5 C.8 D.12.5
3.一艘轮船在A处测得灯塔S在船的南偏东方向,轮船继续向正东航行30海里后到达B处,这时测得灯塔S在船的南偏西方向,则灯塔S离观测点A、B的距离分别是
A.海里、15海里 B.海里、5海里
C.海里、海里 D.海里、海里
4.点关于轴对称的点的坐标是( )
A. B. C. D.
5.的值是( ).
A.1 B. C. D.
6.在中,,,,则的值为( )
A. B. C. D.
7.如图,小明在骑行过程中发现山上有一建筑物.他测得仰角为15°;沿水平笔直的公路向山的方向行驶4千米后,测得该建筑物的仰角为30°,若小明的眼睛与地面的距离忽略不计,则该建筑物离地面的高度为( )
A.2千米 B.2千米 C.2千米 D.千米
8.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长米,背水坡CD的坡度,则背水坡的坡长CD为( )米.
A.20 B. C.10 D.
9.如图,点A(x,4)在第一象限,OA与x轴所夹的锐角为α,cosα=,则tanα的值为( )
A. B. C. D.
10.为了疫情防控工作的需要,某学校在学校门口的大门上方安装了一个人体体外测温摄像头,摄像头到地面的距离米,小明身高米,他在点A测得点D的仰角是在点B测得点D仰角的2倍,已知小明在点B测得的仰角是a,则体温监测有效识别区域的长为( )米.( )
A. B.
C. D.
二、填空题
11.如果是锐角,,那么为___________.
12.如图,在Rt△ABC中,,过A作于点D,若.则tanC的值为___________.
13.锐角中,,则的形状是___________.
14.已知:0°<α<90°,0°<β<90°且sinα=,tanβ=,则cos(β﹣α)=___.
15.如图,的三个顶点分别在边长为1的正方形网格上,则的值为______.
16.如图,半径为3的经过原点O和点,点B是中弦所对优弧上的一点,则的值为______.
17.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,已知托板长,支撑板长,托板固定在支撑板顶端点C处,且,托板可绕点C转动,支撑板可绕点D转动.
(1)若,,求点A到直线的距离为________;
(2)为了观看舒适,保持,在(1)的情况下,将绕点D顺时针旋转,使点B落在直线上即可,求旋转的角度为________.
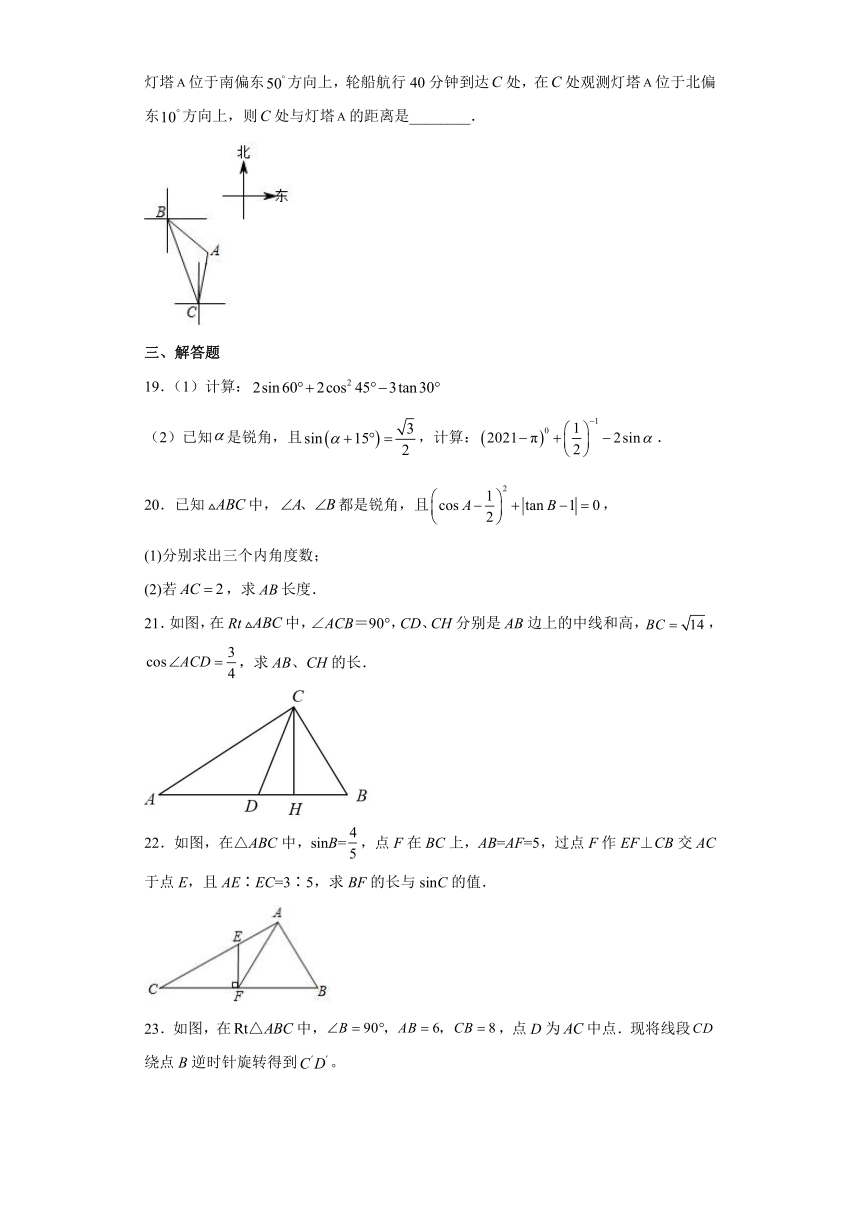
18.如图,轮船从处以每小时60海里的速度沿南偏东方向匀速航行,在处观测灯塔位于南偏东方向上,轮船航行40分钟到达处,在处观测灯塔位于北偏东方向上,则处与灯塔的距离是________.
三、解答题
19.(1)计算:
(2)已知是锐角,且,计算:.
20.已知中,都是锐角,且,
(1)分别求出三个内角度数;
(2)若,求长度.
21.如图,在Rt中,∠ACB=90°,CD、CH分别是AB边上的中线和高,,,求AB、CH的长.
22.如图,在△ABC中,sinB=,点F在BC上,AB=AF=5,过点F作EF⊥CB交AC于点E,且AE∶EC=3∶5,求BF的长与sinC的值.
23.如图,在中,,点D为中点.现将线段绕点B逆时针旋转得到。
(1)若点恰好落在边上,则点到的距离是多少?
(2)若点A恰好在上,则的长为是多少?
24.如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.
(1)求两建筑物底部之间的水平距离BD;
(2)求建筑物CD的高度;(精确到1m,参考数据:sin 69°≈0.93、cos69°≈0.36、tan 69°≈2.70、≈1.73)
25.如图,某大楼的顶部竖有一块广告牌CD,小马同学在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡比i=1:,AB=10米,AE=21米.(测角器的高度忽略不计,参考数据:sin53°
(1)求点B距水平地面AE的高度;
(2)求广告牌的高度CD的长度.(结果保留根号)
参考答案:
1.A
2.A
3.D
过S作于C,在上截取,
∴,
∴,
∵,
∴,
∴,
设,在中,
∵,
∴,,
∵海里,
∴,
解得:,
∴海里,
∴海里,
∴则灯塔S离观测点A、B的距离分别是海里、海里.
4.C
解:,
∴点的坐标为
点关于轴对称的点的坐标是
5.A
解:2sin30°
=2×
=1
6.D
解:在Rt△ABC中,
tan A=,
7.C
如图,由题意得,千米,,
,
,
千米,
,,
在中,千米,
即该建筑物离地面的高度为2千米,
8.A
解:∵迎水坡AB的坡角α=45°,坡长AB=10米,
∴AE=10×sin45°=10(米),
∴DF=AE=10,
∵背水坡CD的坡度i=1:,∠DFC=90°,
∴tan∠C=,
∴∠C=30°,
∴DC=2DF=2AE=20(米),
9.A
解:过A作AB⊥x轴于B,则∠ABO=90°,
∵cosα=,
设OB=3x,则OA=5x,
∵A(x,4),
∴AB=4,
由勾股定理得:,
所以,
解得:x=1,x= -1(负数舍去),
即OB=3,
∴tanα==,
10.B
解:由题意可知:四边形是矩形,
,米,
米,
(米),
在中,,
(米),
在中,,
(米),
(米),
11.
解:∵,
又∵,
∴;
故答案为:.
12.
解:,
设,,
,
,
,
,
,
,
,
,
故答案为:.
13.等边三角形
解:∵,
∴,,
又∵,,
∴,,
∴,
∴,
∴的形状是等边三角形,
故答案为:等边三角形.
14.
∵0°<α<90°,0°<β<90°且sinα=,tanβ=
∴α=30゜,β=60゜
∴
故答案为:
15.
如图,∵,,,
∴,
∴是直角三角形,,
∴
故答案为:
16.
解:连接,如图,
∵点,
∴,
∵,
∴为的直径,
在中,,
∴,
∵,
∴.
故答案为:.
17.
解:(1)如图,过点作于点,
∵,,
∴,
作于点,于点,
∴,,
∵,
∴,
∵,
∴
∴,
∴,
答:点到直线的距离是;
故答案为:
(2)∵,
如图,连接,
∵,,
∴,
∴,
∴,
答:CD旋转的度数为.
故答案为:
18.海里
解:如图,作于.
由题意得,,,(海里),,
则,
∵,
∴,
∴,
∴,
∴,
∵于,
∴(海里),
在直角中,,,
∴(海里).
故答案为:海里.
19.(1)1;(2)
(1)原式
(2)
则
20.(1),,
(2)
(1)
解:
,
,
,
;
(2)
解:如图:过点C作于点D
,
,
.
21.CH的长为,AB的长为.
解:过D作DE⊥AC于E,则∠AED=∠CED=90°,
∵∠ACB=90°,
∴∠AED=∠ACB,
∴DE//BC,
∵CD是△ABC的中线,
∴AD=BD,
∴CE=AE,即AC=2CE
∵,
∴DE=BC=,
∵
∴设CE=3x,CD=4x,
由勾股定理得:
∴=,即x=
∴
∴AC=AE+CE=
∵,即
∴AB=
∵
∴,解得:CH=.
∴CH的长为,AB的长为.
22.6,
分析:过点A作AD⊥CB,垂足为点D,根据解直角三角形的计算解答即可.
详解:过点A作AD⊥CB,垂足为点D,
∵sinB=,
∴cosB=,
在Rt△ABD中,BD=AB cosB=5×=3,
∵AB=AF AD⊥CB,
∴BF=2BD=6,
∵EF⊥CB AD⊥CB,
∴EF∥AD,
∴,
∵AE:EC=3:5DF=BD=3,
∴CF=5,
∴CD=8,
在Rt△ABD中,AD=AB sinB=5×=4,
在Rt△ACD中,AC==4,
∴sinC=.
23.(1);
(2)
(1)如图,连接,
在中,,,,
,
点是的中点,
.
由旋转的性质可知,△,
,,,
,
当点恰好落在边上,如图所示,
过点作于点,过点作交的延长于点,
,
,
.
,
,
.
∴点到的距离是;
(2)当点恰好在上,如图所示,
过点作于点,则.
设,则,
,,
在中,由勾股定理可得,,
解得或.
(舍去)或.
∴点A恰好在上,则.
24.(1)约30米;(2)约63米
(1),∠EAD69°
建筑物底部之间的水平距离BD约30米;
(2)如图,作,
则四边形是矩形
,
建筑物CD的高度约63米
25.(1)5米;(2)米,
解:(1)如图,过点B作BM⊥AE,BN⊥CE,垂足分别为M、N,
由题意可知,∠CBN=45°,∠DAE=53°,i=1:,AB=10米,AE=21米.
∵,
∴∠BAM=30°,
∴BM=AB=5(米),
即点B距水平地面AE的高度为5米;
(2)在Rt△ABM中,
∴BM=AB=5(米)=NE,(米),
∴ME=AM+AE=米=BN,
∵∠CBN=45°,
∴CN=BN=ME=米,
∴CE=CN+NE=米,
在Rt△ADE中,∠DAE=53°,AE=21米,
∴(米),
∴CD=CE-DE米,
一、单选题
1.已知,则锐角α的度数是( )
A.60° B.45° C.30° D.75°
2.在Rt△ACB中,∠C=90°,AB=8,sinA=,则BC的长为( )
A.6 B.7.5 C.8 D.12.5
3.一艘轮船在A处测得灯塔S在船的南偏东方向,轮船继续向正东航行30海里后到达B处,这时测得灯塔S在船的南偏西方向,则灯塔S离观测点A、B的距离分别是
A.海里、15海里 B.海里、5海里
C.海里、海里 D.海里、海里
4.点关于轴对称的点的坐标是( )
A. B. C. D.
5.的值是( ).
A.1 B. C. D.
6.在中,,,,则的值为( )
A. B. C. D.
7.如图,小明在骑行过程中发现山上有一建筑物.他测得仰角为15°;沿水平笔直的公路向山的方向行驶4千米后,测得该建筑物的仰角为30°,若小明的眼睛与地面的距离忽略不计,则该建筑物离地面的高度为( )
A.2千米 B.2千米 C.2千米 D.千米
8.如图所示,某拦水大坝的横断面为梯形ABCD,AE,DF为梯形的高,其中迎水坡AB的坡角α=45°,坡长米,背水坡CD的坡度,则背水坡的坡长CD为( )米.
A.20 B. C.10 D.
9.如图,点A(x,4)在第一象限,OA与x轴所夹的锐角为α,cosα=,则tanα的值为( )
A. B. C. D.
10.为了疫情防控工作的需要,某学校在学校门口的大门上方安装了一个人体体外测温摄像头,摄像头到地面的距离米,小明身高米,他在点A测得点D的仰角是在点B测得点D仰角的2倍,已知小明在点B测得的仰角是a,则体温监测有效识别区域的长为( )米.( )
A. B.
C. D.
二、填空题
11.如果是锐角,,那么为___________.
12.如图,在Rt△ABC中,,过A作于点D,若.则tanC的值为___________.
13.锐角中,,则的形状是___________.
14.已知:0°<α<90°,0°<β<90°且sinα=,tanβ=,则cos(β﹣α)=___.
15.如图,的三个顶点分别在边长为1的正方形网格上,则的值为______.
16.如图,半径为3的经过原点O和点,点B是中弦所对优弧上的一点,则的值为______.
17.如图1是一种手机平板支架,由托板、支撑板和底座构成,手机放置在托板上,图2是其侧面结构示意图,已知托板长,支撑板长,托板固定在支撑板顶端点C处,且,托板可绕点C转动,支撑板可绕点D转动.
(1)若,,求点A到直线的距离为________;
(2)为了观看舒适,保持,在(1)的情况下,将绕点D顺时针旋转,使点B落在直线上即可,求旋转的角度为________.
18.如图,轮船从处以每小时60海里的速度沿南偏东方向匀速航行,在处观测灯塔位于南偏东方向上,轮船航行40分钟到达处,在处观测灯塔位于北偏东方向上,则处与灯塔的距离是________.
三、解答题
19.(1)计算:
(2)已知是锐角,且,计算:.
20.已知中,都是锐角,且,
(1)分别求出三个内角度数;
(2)若,求长度.
21.如图,在Rt中,∠ACB=90°,CD、CH分别是AB边上的中线和高,,,求AB、CH的长.
22.如图,在△ABC中,sinB=,点F在BC上,AB=AF=5,过点F作EF⊥CB交AC于点E,且AE∶EC=3∶5,求BF的长与sinC的值.
23.如图,在中,,点D为中点.现将线段绕点B逆时针旋转得到。
(1)若点恰好落在边上,则点到的距离是多少?
(2)若点A恰好在上,则的长为是多少?
24.如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.
(1)求两建筑物底部之间的水平距离BD;
(2)求建筑物CD的高度;(精确到1m,参考数据:sin 69°≈0.93、cos69°≈0.36、tan 69°≈2.70、≈1.73)
25.如图,某大楼的顶部竖有一块广告牌CD,小马同学在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡比i=1:,AB=10米,AE=21米.(测角器的高度忽略不计,参考数据:sin53°
(1)求点B距水平地面AE的高度;
(2)求广告牌的高度CD的长度.(结果保留根号)
参考答案:
1.A
2.A
3.D
过S作于C,在上截取,
∴,
∴,
∵,
∴,
∴,
设,在中,
∵,
∴,,
∵海里,
∴,
解得:,
∴海里,
∴海里,
∴则灯塔S离观测点A、B的距离分别是海里、海里.
4.C
解:,
∴点的坐标为
点关于轴对称的点的坐标是
5.A
解:2sin30°
=2×
=1
6.D
解:在Rt△ABC中,
tan A=,
7.C
如图,由题意得,千米,,
,
,
千米,
,,
在中,千米,
即该建筑物离地面的高度为2千米,
8.A
解:∵迎水坡AB的坡角α=45°,坡长AB=10米,
∴AE=10×sin45°=10(米),
∴DF=AE=10,
∵背水坡CD的坡度i=1:,∠DFC=90°,
∴tan∠C=,
∴∠C=30°,
∴DC=2DF=2AE=20(米),
9.A
解:过A作AB⊥x轴于B,则∠ABO=90°,
∵cosα=,
设OB=3x,则OA=5x,
∵A(x,4),
∴AB=4,
由勾股定理得:,
所以,
解得:x=1,x= -1(负数舍去),
即OB=3,
∴tanα==,
10.B
解:由题意可知:四边形是矩形,
,米,
米,
(米),
在中,,
(米),
在中,,
(米),
(米),
11.
解:∵,
又∵,
∴;
故答案为:.
12.
解:,
设,,
,
,
,
,
,
,
,
,
故答案为:.
13.等边三角形
解:∵,
∴,,
又∵,,
∴,,
∴,
∴,
∴的形状是等边三角形,
故答案为:等边三角形.
14.
∵0°<α<90°,0°<β<90°且sinα=,tanβ=
∴α=30゜,β=60゜
∴
故答案为:
15.
如图,∵,,,
∴,
∴是直角三角形,,
∴
故答案为:
16.
解:连接,如图,
∵点,
∴,
∵,
∴为的直径,
在中,,
∴,
∵,
∴.
故答案为:.
17.
解:(1)如图,过点作于点,
∵,,
∴,
作于点,于点,
∴,,
∵,
∴,
∵,
∴
∴,
∴,
答:点到直线的距离是;
故答案为:
(2)∵,
如图,连接,
∵,,
∴,
∴,
∴,
答:CD旋转的度数为.
故答案为:
18.海里
解:如图,作于.
由题意得,,,(海里),,
则,
∵,
∴,
∴,
∴,
∴,
∵于,
∴(海里),
在直角中,,,
∴(海里).
故答案为:海里.
19.(1)1;(2)
(1)原式
(2)
则
20.(1),,
(2)
(1)
解:
,
,
,
;
(2)
解:如图:过点C作于点D
,
,
.
21.CH的长为,AB的长为.
解:过D作DE⊥AC于E,则∠AED=∠CED=90°,
∵∠ACB=90°,
∴∠AED=∠ACB,
∴DE//BC,
∵CD是△ABC的中线,
∴AD=BD,
∴CE=AE,即AC=2CE
∵,
∴DE=BC=,
∵
∴设CE=3x,CD=4x,
由勾股定理得:
∴=,即x=
∴
∴AC=AE+CE=
∵,即
∴AB=
∵
∴,解得:CH=.
∴CH的长为,AB的长为.
22.6,
分析:过点A作AD⊥CB,垂足为点D,根据解直角三角形的计算解答即可.
详解:过点A作AD⊥CB,垂足为点D,
∵sinB=,
∴cosB=,
在Rt△ABD中,BD=AB cosB=5×=3,
∵AB=AF AD⊥CB,
∴BF=2BD=6,
∵EF⊥CB AD⊥CB,
∴EF∥AD,
∴,
∵AE:EC=3:5DF=BD=3,
∴CF=5,
∴CD=8,
在Rt△ABD中,AD=AB sinB=5×=4,
在Rt△ACD中,AC==4,
∴sinC=.
23.(1);
(2)
(1)如图,连接,
在中,,,,
,
点是的中点,
.
由旋转的性质可知,△,
,,,
,
当点恰好落在边上,如图所示,
过点作于点,过点作交的延长于点,
,
,
.
,
,
.
∴点到的距离是;
(2)当点恰好在上,如图所示,
过点作于点,则.
设,则,
,,
在中,由勾股定理可得,,
解得或.
(舍去)或.
∴点A恰好在上,则.
24.(1)约30米;(2)约63米
(1),∠EAD69°
建筑物底部之间的水平距离BD约30米;
(2)如图,作,
则四边形是矩形
,
建筑物CD的高度约63米
25.(1)5米;(2)米,
解:(1)如图,过点B作BM⊥AE,BN⊥CE,垂足分别为M、N,
由题意可知,∠CBN=45°,∠DAE=53°,i=1:,AB=10米,AE=21米.
∵,
∴∠BAM=30°,
∴BM=AB=5(米),
即点B距水平地面AE的高度为5米;
(2)在Rt△ABM中,
∴BM=AB=5(米)=NE,(米),
∴ME=AM+AE=米=BN,
∵∠CBN=45°,
∴CN=BN=ME=米,
∴CE=CN+NE=米,
在Rt△ADE中,∠DAE=53°,AE=21米,
∴(米),
∴CD=CE-DE米,
