2022-2023学年京改版八年级数学下册14.5一次函数的图像 达标测评 (无答案)
文档属性
| 名称 | 2022-2023学年京改版八年级数学下册14.5一次函数的图像 达标测评 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 201.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 00:00:00 | ||
图片预览



文档简介
京改版八年级数学下册14.5一次函数的图像达标测评
一、单选题
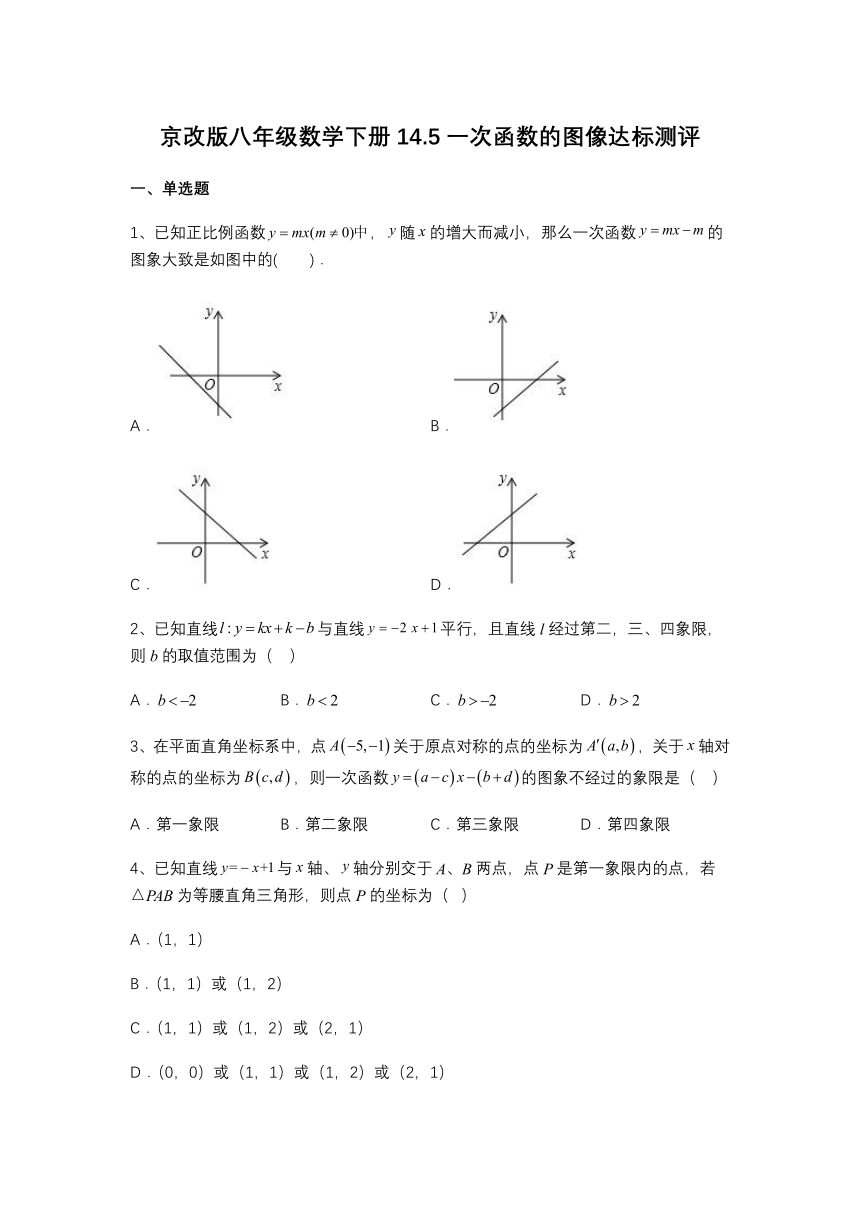
1、已知正比例函数,随的增大而减小,那么一次函数的图象大致是如图中的( ).
A. B.
C. D.
2、已知直线与直线平行,且直线l经过第二,三、四象限,则b的取值范围为( )
A. B. C. D.
3、在平面直角坐标系中,点关于原点对称的点的坐标为,关于轴对称的点的坐标为,则一次函数的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4、已知直线与轴、轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )
A.(1,1)
B.(1,1)或(1,2)
C.(1,1)或(1,2)或(2,1)
D.(0,0)或(1,1)或(1,2)或(2,1)
5、下列关于一次函数的说法,错误的是( )
A.图象经过第一、二、四象限
B.随的增大而减小
C.图象与轴交于点
D.当时,
6、如图,在矩形ABCD中,,.点P从点A出发,以2cm/s的速度在矩形的边上沿运动,当点P与点D重合时停止运动.设运动的时间为(单位:s),的面积为S(单位:),则S随t变化的函数图象大致为( )
B.
C. D.
7、在平面直角坐标系xOy中,直线y=2x+2和直线y=-2x+4分别交x轴于点A和点B,则下列直线中,与x轴的交点在线段AB上的是( )
A.y=x+2 B. C.y=4x-12 D.
8、如果一个正比例函数的图象经过不同象限的两点A(3,m)、B(n,﹣2),那么一定有( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
二、填空题
1、若一次函数(k为常数,)的图象经过第二、三、四象限,则k的值可以是_________(写出一个即可).
2、若一次函数的图象不过第一象限,则k的取值范围是_______.
3、在同一直角坐标系中,对于以下四个函数①;②;③;④的图象,下列说法正确的个数是 ___________.
(1)①③④三个函数的图象中 ,当时,;
(2)在x轴上交点相同的是②和④;
(3)②中的点到x轴的距离比到y轴的距离都要大1;
(4)函数①和②的图象和x轴围成的图形面积为2.
4、已知A(2,3),B(3,6),若直线 与线段相交, 则的取值范围是______.
5、正比例函数的图象过第一、三象限,则的取值范围是______.
6、已知一次函数的图象经过第一、二、四象限,则化简__________.
三、解答题
1、如图,直线y= x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y= x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.
2、已知关于x的方程mx-2=3x+n有无数个解.
(1)求出m、n的值.
(2)求一次函数y=mx+n与坐标轴围成的三角形的面积.
3、如图,A点坐标为,直线经过点和点,交x轴于点D.
(1)求直线的函数表达式.
(2)点M在直线上,且满足,求点M的坐标.
4、已知一次函数y=kx+b的图象如图所示.
(1)求k,b的值;
(2)请在图中作出函数y=2x+6的图象;
(3)利用图象解答下列问题:当y=kx+b的函数值大于y=2x+6的函数值时,求x的取值范围.
5、数学中,常对同一图形的面积用两种不同的方法计算,从而建立相等关系,这是一种重要的数学方法.如图1,两个直角边分别为a、b、斜边长为c的直角三角形和一个两条直角边都是c的直角三角形拼成一个梯形.
解:有三个直角三角形其面积分别为,和,
直角梯形的面积为.
由图形可知:=+.
整理得(a+b)2=2ab+c2,a2+b2+2ab=c2+2ab.
∴a2+b2=c2.
故结论为:直角边长分别为a、b斜边为c的直角三角形中a2+b2=c2.
(1)[类比尝试]
如图2,在4×4的正方形网格中,每个小正方形的边长均为1,点A、B、C都在格点上,若BD是△ABC的边AC上的高,求:
①△ABC的面积;
②BD的长.
(2)[拓展探究]
如图3坐标系中,直线l1:与x轴、y轴分别交于点A和B,直线l2经过坐标原点,且l2⊥l1,垂足为C.求:
①写出点A和点B的坐标.
②点C到x轴的距离.
一、单选题
1、已知正比例函数,随的增大而减小,那么一次函数的图象大致是如图中的( ).
A. B.
C. D.
2、已知直线与直线平行,且直线l经过第二,三、四象限,则b的取值范围为( )
A. B. C. D.
3、在平面直角坐标系中,点关于原点对称的点的坐标为,关于轴对称的点的坐标为,则一次函数的图象不经过的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
4、已知直线与轴、轴分别交于A、B两点,点P是第一象限内的点,若△PAB为等腰直角三角形,则点P的坐标为( )
A.(1,1)
B.(1,1)或(1,2)
C.(1,1)或(1,2)或(2,1)
D.(0,0)或(1,1)或(1,2)或(2,1)
5、下列关于一次函数的说法,错误的是( )
A.图象经过第一、二、四象限
B.随的增大而减小
C.图象与轴交于点
D.当时,
6、如图,在矩形ABCD中,,.点P从点A出发,以2cm/s的速度在矩形的边上沿运动,当点P与点D重合时停止运动.设运动的时间为(单位:s),的面积为S(单位:),则S随t变化的函数图象大致为( )
B.
C. D.
7、在平面直角坐标系xOy中,直线y=2x+2和直线y=-2x+4分别交x轴于点A和点B,则下列直线中,与x轴的交点在线段AB上的是( )
A.y=x+2 B. C.y=4x-12 D.
8、如果一个正比例函数的图象经过不同象限的两点A(3,m)、B(n,﹣2),那么一定有( )
A.m>0,n>0 B.m>0,n<0 C.m<0,n>0 D.m<0,n<0
二、填空题
1、若一次函数(k为常数,)的图象经过第二、三、四象限,则k的值可以是_________(写出一个即可).
2、若一次函数的图象不过第一象限,则k的取值范围是_______.
3、在同一直角坐标系中,对于以下四个函数①;②;③;④的图象,下列说法正确的个数是 ___________.
(1)①③④三个函数的图象中 ,当时,;
(2)在x轴上交点相同的是②和④;
(3)②中的点到x轴的距离比到y轴的距离都要大1;
(4)函数①和②的图象和x轴围成的图形面积为2.
4、已知A(2,3),B(3,6),若直线 与线段相交, 则的取值范围是______.
5、正比例函数的图象过第一、三象限,则的取值范围是______.
6、已知一次函数的图象经过第一、二、四象限,则化简__________.
三、解答题
1、如图,直线y= x+10与x轴、y轴分别交于点B,C,点A的坐标为(8,0),P(x,y)是直线y= x+10在第一象限内一个动点.
(1)求△OPA的面积S与x的函数关系式,并写出自变量x的取值范围;
(2)当△OPA的面积为10时,求点P的坐标.
2、已知关于x的方程mx-2=3x+n有无数个解.
(1)求出m、n的值.
(2)求一次函数y=mx+n与坐标轴围成的三角形的面积.
3、如图,A点坐标为,直线经过点和点,交x轴于点D.
(1)求直线的函数表达式.
(2)点M在直线上,且满足,求点M的坐标.
4、已知一次函数y=kx+b的图象如图所示.
(1)求k,b的值;
(2)请在图中作出函数y=2x+6的图象;
(3)利用图象解答下列问题:当y=kx+b的函数值大于y=2x+6的函数值时,求x的取值范围.
5、数学中,常对同一图形的面积用两种不同的方法计算,从而建立相等关系,这是一种重要的数学方法.如图1,两个直角边分别为a、b、斜边长为c的直角三角形和一个两条直角边都是c的直角三角形拼成一个梯形.
解:有三个直角三角形其面积分别为,和,
直角梯形的面积为.
由图形可知:=+.
整理得(a+b)2=2ab+c2,a2+b2+2ab=c2+2ab.
∴a2+b2=c2.
故结论为:直角边长分别为a、b斜边为c的直角三角形中a2+b2=c2.
(1)[类比尝试]
如图2,在4×4的正方形网格中,每个小正方形的边长均为1,点A、B、C都在格点上,若BD是△ABC的边AC上的高,求:
①△ABC的面积;
②BD的长.
(2)[拓展探究]
如图3坐标系中,直线l1:与x轴、y轴分别交于点A和B,直线l2经过坐标原点,且l2⊥l1,垂足为C.求:
①写出点A和点B的坐标.
②点C到x轴的距离.
同课章节目录
