人教A版(2019) 选择性必修第一册 高二培优阶段训练:专题02 空间向量基本定理及范围最值(含解析)
文档属性
| 名称 | 人教A版(2019) 选择性必修第一册 高二培优阶段训练:专题02 空间向量基本定理及范围最值(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-13 21:10:50 | ||
图片预览



文档简介
培优第一阶——基础过关练
1.(2022·全国·高二课时练习)若为空间的一个基底,则下列各组向量中一定能构成空间的一个基底的是______.(填序号)
①,,; ②,,;
③,,; ④,,.
2.(2022·浙江·高二开学考试)在平行六面体中,为的中点,为的中点,,则( )
A. B.
C. D.
3.(2022·江苏镇江·高二开学考试)已知四棱锥的底面是平行四边形,侧棱、、上分别有一点、、,且满足,,,若、、、四点共面,则实数__________.
4.(2022·全国·高二课时练习)在空间四点O,A,B,C中,若是空间的一个基底,则下列命题不正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点不共面
D.O,A,B,C四点中任意三点不共线
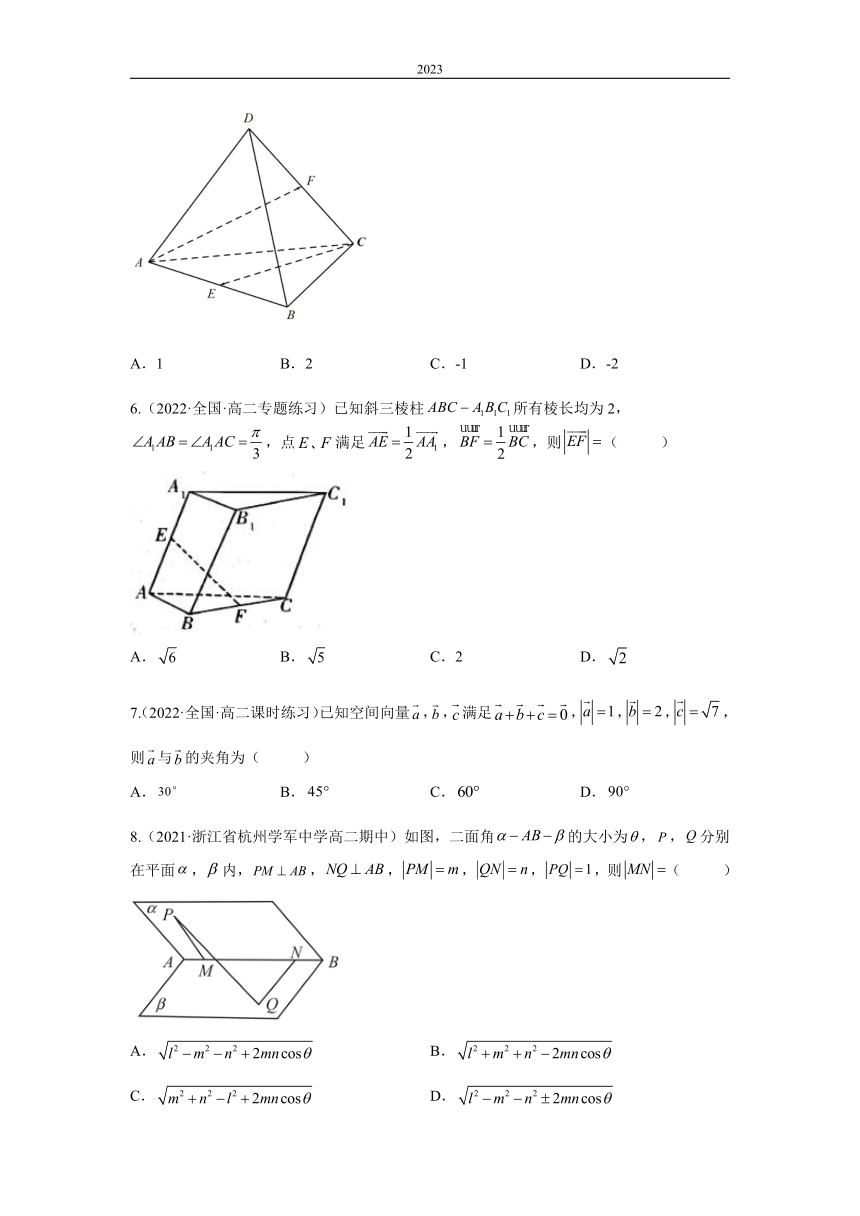
5.(2022·全国·高二课时练习)已知四面体,所有棱长均为2,点E,F分别为棱AB,CD的中点,则( )
A.1 B.2 C.-1 D.-2
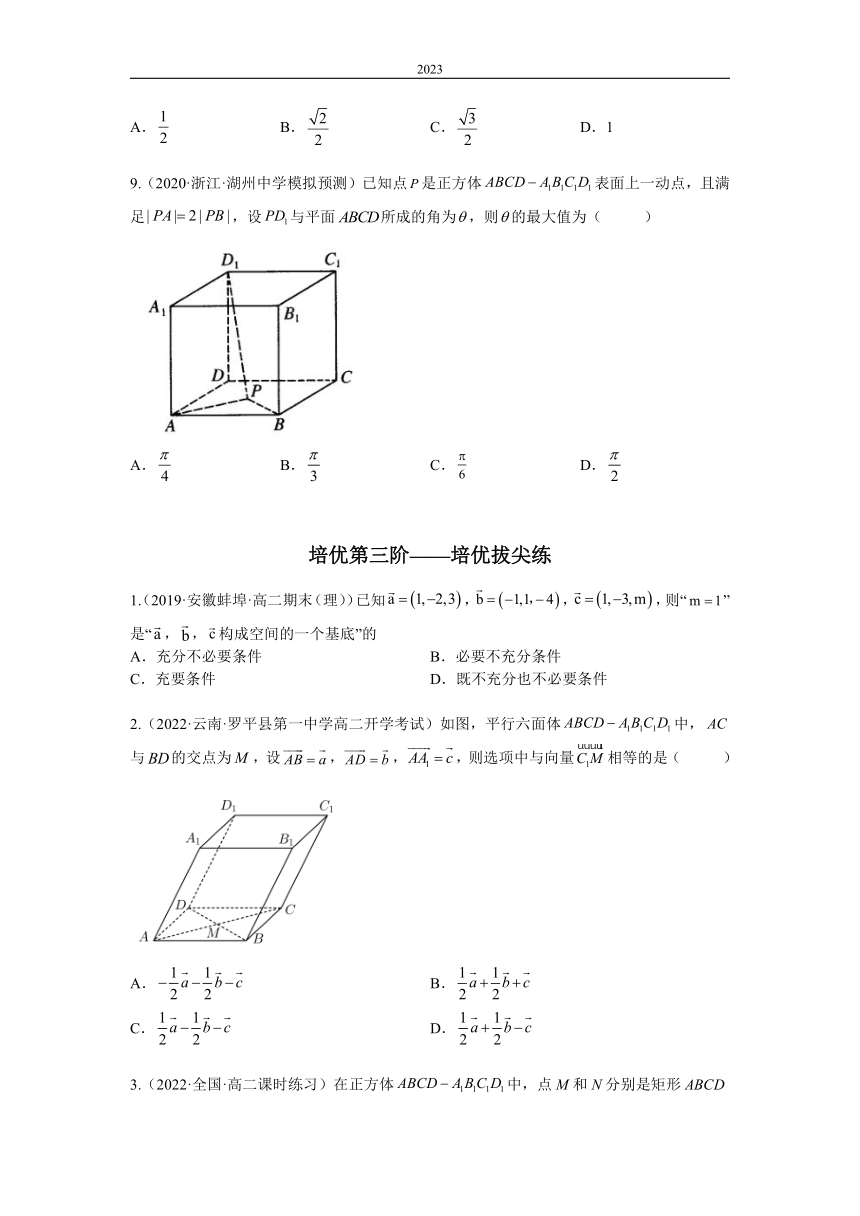
6.(2022·全国·高二专题练习)已知斜三棱柱所有棱长均为2,,点 满足,,则( )
A. B. C.2 D.
7.(2022·全国·高二课时练习)已知空间向量,,满足,,,,则与的夹角为( )
A. B. C. D.
8.(2021·浙江省杭州学军中学高二期中)如图,二面角的大小为,,分别在平面,内,,,,,,则( )
A. B.
C. D.
9.(2022·全国·高二课时练习)已知,.若与的夹角为钝角,则实数的取值范围是________.
培优第二阶——能力提升练
1.(2021·全国·高二课时练习)设且是空间的一组基底,给出下列向量组:
①;② ③ ④
其中可以作为空间的基底的向量组是___________(填序号).
2.(2022·福建·厦门海沧实验中学高二期中)如图,在四面体中,,,,且,,则( )
A. B.
C. D.
3.(2021·福建·厦门双十中学高二期中)已知,若三向量共面,则实数=_____.
4.(2021·河北·石家庄市第十二中学高二期中)下列关于空间向量的说法中,正确的有___________.
①若向量,与空间任意向量都不能构成基底,则
②若非零向量,,满足,,,则有
③是,共线的充分不必要条件
④若,共线,则
5.(2022·全国·高二课时练习)如图,在三棱柱中,底面为正三角形,侧棱垂直于底面,.若E是棱的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
6.(2021·安徽·高二阶段练习)在平行六面体中,,,,,,则AM的长为( )
A. B. C. D.
7.(2022·全国·高二专题练习)已知是棱长为4的正方体内切球的一条直径,点在正方体表面上运动,则的取值范围为( )
A. B. C. D.
8.(2022·河南·洛宁县第一高级中学高二阶段练习)如图,三棱锥各棱的棱长是1,点是棱的中点,点在棱上,且,则的最小值为( )
A. B. C. D.1
9.(2020·浙江·湖州中学模拟预测)已知点是正方体表面上一动点,且满足,设与平面所成的角为,则的最大值为( )
A. B. C. D.
培优第三阶——培优拔尖练
1.(2019·安徽蚌埠·高二期末(理))已知,,,则“”是“,,构成空间的一个基底”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.(2022·云南·罗平县第一中学高二开学考试)如图,平行六面体中,与的交点为,设,,,则选项中与向量相等的是( )
A. B.
C. D.
3.(2022·全国·高二课时练习)在正方体中,点M和N分别是矩形ABCD和的中心,若点P满足,其中,且,则点P可以是正方体表面上的点________.
4.(2022全国·高二专题练习)下列命题正确的是( )
A.若与共线,与线,则与共线
B.向量,,共面,即它们所在的直线共面
C.若∥,则存在唯一的实数λ,使=λ
D.零向量是模为0,方向任意的向量
5.(2022·全国·高二课时练习)如图所示,空间四边形的各边和对角线长均相等,E是BC的中点,那么( ).
A. B.
C. D.与不能比较大小
6.(2022·全国·高二单元测试)如图在平行六面体中,底面 是边长为1的正方形,侧棱且,则 ( )
A. B. C. D.
7.(2021·全国·高二专题练习)已知棱长为的正方体,点在空间直角坐标系的轴上移动,点在平面上移动,则的最大值是( )
A. B. C. D.
8.(2022·全国·高二专题练习)如图,已知正方体的棱长为1,则线段上的动点P到直线的距离的最小值为( )
A.1 B. C. D.
9.(2022·江西鹰潭·高二期末(理))如图,在三棱锥中,,,,点在平面内,且,设异面直线与所成的角为,则的最大值为( )
A. B. C. D.
培优第一阶——基础过关练
1.(2022·全国·高二课时练习)若为空间的一个基底,则下列各组向量中一定能构成空间的一个基底的是______.(填序号)
①,,; ②,,;
③,,; ④,,.
【答案】③
【分析】根据空间向量基本定理判断可得;
【详解】解:由空间向量基本定理得:
对于①,,所以,,三个向量共面;
对于②,,所以,,三个向量共面;
对于③,因为为空间的一个基底,所以与不共线,所以,也不共线,
且与 、共面,与、共面,又、、三个向量不共面,
所以,,不共面,故,,可以作为一组基底;
对于④,,所以,,三个向量共面,
故答案为:③.
2.(2022·浙江·高二开学考试)在平行六面体中,为的中点,为的中点,,则( )
A. B.
C. D.
【答案】C
【分析】设,根据空间向量的线性运算表达,再联立求解即可.
【详解】设则.
所以,,所以.
故选:C
3.(2022·江苏镇江·高二开学考试)已知四棱锥的底面是平行四边形,侧棱、、上分别有一点、、,且满足,,,若、、、四点共面,则实数__________.
【答案】##
【分析】根据四点共面的等价条件以及,可得出关于的两个表达式,可得出关于的方程组,即可解得实数的值.
【详解】因为、、、四点共面,则存在、使得,
所以,,
所以,,
因为,即,所以,,
因为,即,
所以,,可得,解得.故答案为:.
4.(2022·全国·高二课时练习)在空间四点O,A,B,C中,若是空间的一个基底,则下列命题不正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点不共面
D.O,A,B,C四点中任意三点不共线
【答案】B
【分析】根据基底的含义,非零向量不在同一平面内,即O,A,B,C四点不共面,即可判断
【详解】因为为基底,所以非零向量不在同一平面内,
即O,A,B,C四点不共面,
所以A、C、D选项说法正确,B错误.
故选:B
5.(2022·全国·高二课时练习)已知四面体,所有棱长均为2,点E,F分别为棱AB,CD的中点,则( )
A.1 B.2 C.-1 D.-2
【答案】D
【分析】在四面体中,取定一组基底向量,表示出,,再借助空间向量数量积计算作答.
【详解】四面体的所有棱长均为2,则向量不共面,两两夹角都为,
则,
因点E,F分别为棱AB,CD的中点,则,,
,
所以.
故选:D
6.(2022·全国·高二专题练习)已知斜三棱柱所有棱长均为2,,点 满足,,则( )
A. B. C.2 D.
【答案】D
【分析】以向量为基底向量,则,根据条件由向量的数量积的运算性质,两边平方可得答案.
【详解】以向量为基底向量,
所以 所以 故选:D
7.(2022·全国·高二课时练习)已知空间向量,,满足,,,,则与的夹角为( )
A. B. C. D.
【答案】C
【分析】将,两边平方,利用空间向量的数量积即可得选项.
【详解】设与的夹角为.由,得,两边平方,得,
所以,解得,又,所以,
故选:C.
8.(2021·浙江省杭州学军中学高二期中)如图,二面角的大小为,,分别在平面,内,,,,,,则( )
A. B.
C. D.
【答案】A
【分析】由向量加法可得,再利用向量的模长公式,结合向量数量积公式,化简整理式子即可得到答案.
【详解】,,
与夹角大小为二面角的大小, ,,
又利用向量加法运算知,
,
,即
解得:
故选:A.
9.(2022·全国·高二课时练习)已知,.若与的夹角为钝角,则实数的取值范围是________.
【答案】
【分析】由,,根据与的夹角为钝角,由且求解.
【详解】因为,,所以,
因为与的夹角为钝角,所以且,由,得,
所以.若与的夹角为,则存在,使,即,
所以,解得,故答案为:
培优第二阶——能力提升练
1.(2021·全国·高二课时练习)设且是空间的一组基底,给出下列向量组:
①;② ③ ④
其中可以作为空间的基底的向量组是___________(填序号).
【答案】②③④
【分析】作一个平行六面体,用共点A的三条棱的向量表示已知的基底向量,求出图形中表示的向量,观察图形判断作答.
【详解】如图,平行六面体中,设,
则,,因四点共面,则向量共面,
而四点不共面,则向量不共面,又四点不共面,则不共面,
四点不共面,则也不共面,
所以可以作为空间的基底的向量组是②③④.
故答案为:②③④
2.(2022·福建·厦门海沧实验中学高二期中)如图,在四面体中,,,,且,,则( )
A. B.
C. D.
【答案】C
【分析】由平面向量的线性运算求解.
【详解】连接,因为,所以,因为,所以,
所以.故选:C.
3.(2021·福建·厦门双十中学高二期中)已知,若三向量共面,则实数=_____.
【答案】
【分析】由题意结合向量基本定理得到方程组,求解方程组即可确定的值.
【详解】由题意可知,存在实数满足:,
据此可得方程组:,求解方程组可得:.
故答案为.
4.(2021·河北·石家庄市第十二中学高二期中)下列关于空间向量的说法中,正确的有___________.
①若向量,与空间任意向量都不能构成基底,则
②若非零向量,,满足,,,则有
③是,共线的充分不必要条件
④若,共线,则
【答案】①③
【分析】由空间向量基本定理可判断①;根据空间向量的位置关系可判断②;由向量的数量积以及充分条件和必要条件的定义可判断③;根据共线向量的定义可判断④,进而可得正确答案.
【详解】对于①:若向量,与空间任意向量都不能构成基底,只能两个向量为共线向量,即,故①正确;
对于②:若非零向量,,满足,,,则与不一定共线,故②不正确;
对于③:由可得:
,可得,即,所以,反向共线,故充分性成立,若,共线则,当时,不成立,故是,共线的充分不必要条件,故③正确;
对于④:若,共线,则或与重合,故④不正确;
所以正确的有①③,
故答案为:①③.
5.(2022·全国·高二课时练习)如图,在三棱柱中,底面为正三角形,侧棱垂直于底面,.若E是棱的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】以为基底表示出,利用向量夹角公式计算出异面直线与所成角的余弦值.
【详解】设,则构成空间的一个基底,
,,
.所以异面直线与所成角的余弦值为.故选:A
6.(2021·安徽·高二阶段练习)在平行六面体中,,,,,,则AM的长为( )
A. B. C. D.
【答案】C
【分析】由题知,再求向量的模即可得答案.
【详解】解:∵,
∴ ,
∴.
故选:C.
7.(2022·全国·高二专题练习)已知是棱长为4的正方体内切球的一条直径,点在正方体表面上运动,则的取值范围为( )
A. B. C. D.
【答案】C
【分析】利用向量的线性运算和数量积运算可得,根据正方体的特点确定最大值和最小值,即可求解.
【详解】设正方体内切球的球心为,则,
,
因为MN是正方体内切球的一条直径,
所以,,
所以,
又点Р在正方体表面上运动,
所以当为正方体顶点时,最大,且最大值为;
当为内切球与正方体的切点时,最小,且最小值为;
所以,
所以的取值范围为,
故选:C.
8.(2022·河南·洛宁县第一高级中学高二阶段练习)如图,三棱锥各棱的棱长是1,点是棱的中点,点在棱上,且,则的最小值为( )
A. B. C. D.1
【答案】B
【分析】首先在中利用余弦定理求出,然后由空间向量的运算法则可得,变形可得,由二次函数的知识可得答案.
【详解】根据题意,在中, ,所以
所以==
则时,取得最小值,则的最小值为.故选:B
9.(2020·浙江·湖州中学模拟预测)已知点是正方体表面上一动点,且满足,设与平面所成的角为,则的最大值为( )
A. B. C. D.
【答案】A
【分析】建立空间直角坐标系,设出点的坐标,根据已知条件求得动点的轨迹方程,再由直线与平面的夹角可得出最值.
【详解】以为坐标原点,,,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,设正方体的边长为2,,则,因为,
所以,即
,所以点的轨迹为以点为球心、为半径的球与正方体表面的交线,
即为如图的,,,要使得与底面所成的角最大,
则与底面的交点到点的距离最短,从而点在上,且在上,
则,从而,所以的最大值为,
故选:A.
培优第三阶——培优拔尖练
1.(2019·安徽蚌埠·高二期末(理))已知,,,则“”是“,,构成空间的一个基底”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【分析】由共面向量定理可得::当“”时,,易得:,,不共面,即,,能构成空间的一个基底,
当,,能构成空间的一个基底,则,,不共面,解得:,综合得解
【详解】解:当“”时,,
易得:,,不共面,即,,能构成空间的一个基底,
即“”是“,,构成空间的一个基底”的充分条件,
当,,能构成空间的一个基底,则,,不共面,
设,,共面,
即,解得:,即,
即,,能构成空间的一个基底时,m的取值范围为:,
即当,,能构成空间的一个基底,不能推出,
即“”是“,,构成空间的一个基底”的不必要条件
综合得:“”是“,,构成空间的一个基底”的充分不必要条件,
故选A.
2.(2022·云南·罗平县第一中学高二开学考试)如图,平行六面体中,与的交点为,设,,,则选项中与向量相等的是( )
A. B.
C. D.
【答案】A
【分析】根据空间向量线性运算法则计算可得.
【详解】解:平行六面体中,与的交点为,设,,,
所以,
则,
所以.
故选:A.
3.(2022·全国·高二课时练习)在正方体中,点M和N分别是矩形ABCD和的中心,若点P满足,其中,且,则点P可以是正方体表面上的点________.
【答案】(或C或边上的任意一点)
【分析】因为点P满足,其中,且,所以点三点共面,只需要找到平面与正方体表面的交线即可.
【详解】解:因为点P满足,其中,且,
所以点三点共面,
因为点M和N分别是矩形ABCD和的中心,
所以,
连接,则,所以即为经过三点的平面与正方体的截面,
故点P可以是正方体表面上的点(或C或边上的任意一点)
故答案为:(或C或边上的任意一点)
4.(2021·全国·高二专题练习)下列命题正确的是( )
A.若与共线,与线,则与共线
B.向量,,共面,即它们所在的直线共面
C.若∥,则存在唯一的实数λ,使=λ
D.零向量是模为0,方向任意的向量
【答案】D
【分析】假设为零向量,可判断选项A;
根据向量的特征,可判断选项B;
根据向量共线定理,可判断选项C;
根据零向量的定义,可判断选项D.
【详解】由于零向量与任意向量共线,所以若为零向量,则与关系不确定,A错;
因为向量是可以平行移动的,因此向量共面时,它们所在的直线不一定共面,B错;
共线向量定理中,当不是零向量时,才存在唯一的实数λ,使=λ,否则λ可能不存在,C错;
根据零向量的定义可知,零向量的模为0,方向是任意的,D显然正确.
故选:D.
5.(2022·全国·高二课时练习)如图所示,空间四边形的各边和对角线长均相等,E是BC的中点,那么( ).
A. B.
C. D.与不能比较大小
【答案】C
【分析】由题设易得,且,应用向量数量积的运算律化简,进而比较它们的大小关系.
【详解】∵E是BC的中点,,
∴,即.
不妨设空间四边形的各边和对角线长均为1,又,,两两之间的夹角均为60°,
∴.
故.
故选:C
6.(2022·全国·高二单元测试)如图在平行六面体中,底面 是边长为1的正方形,侧棱且,则 ( )
A. B. C. D.
【答案】B
【解析】先求出 ,,,,,,再计算即可.
【详解】解:因为底面是边长为1的正方形,侧棱且,
则 ,,,,,,
则
故选:B.
7.(2021·全国·高二专题练习)已知棱长为的正方体,点在空间直角坐标系的轴上移动,点在平面上移动,则的最大值是( )
A. B. C. D.
【答案】D
【分析】取的中点,连接,求得,取的中点,连接、、、、、,求得,求出的最大值,分析可得,即可求得结果.
【详解】取的中点,连接,如下图所示:
因为平面,平面,则,
因为为的中点且,故,
取的中点,连接、、、、、,如下图所示:
因为为的中点且四边形为正方形,故为的中点,
又因为为的中点,故,
所以,,当且仅当、、三点共线且在线段上时,等号成立,
所以,
.因此,的最大值为.故选:D.
8.(2022·全国·高二专题练习)如图,已知正方体的棱长为1,则线段上的动点P到直线的距离的最小值为( )
A.1 B. C. D.
【答案】D
【分析】利用坐标法,设,可得动点P到直线的距离为,然后利用二次函数的性质即得.
【详解】如图建立空间直角坐标系,则,
设,则,∴动点P到直线的距离为
,当时取等号,
即线段上的动点P到直线的距离的最小值为.故选:D.
9.(2022·江西鹰潭·高二期末(理))如图,在三棱锥中,,,,点在平面内,且,设异面直线与所成的角为,则的最大值为( )
A. B. C. D.
【答案】D
【分析】设线段的中点为,连接,过点在平面内作,垂足为点,证明出平面,然后以点为坐标原点,、、分别为、、轴的正方向建立空间直角坐标系,设,其中,且,求出的最大值,利用空间向量法可求得的最大值.
【详解】设线段的中点为,连接,
,为的中点,则,
,则,,同理可得,,
,平面,
过点在平面内作,垂足为点,
因为,所以,为等边三角形,故为的中点,
平面,平面,则,
,,平面,
以点为坐标原点,、、分别为、、轴的正方向建立如下图所示的空间直角坐标系,
因为是边长为的等边三角形,为的中点,则,
则、、、,由于点在平面内,
可设,
其中,且,从而,
因为,则,所以,,
故当时,有最大值,即,
故,即有最大值,
所以,.故选:D.
1.(2022·全国·高二课时练习)若为空间的一个基底,则下列各组向量中一定能构成空间的一个基底的是______.(填序号)
①,,; ②,,;
③,,; ④,,.
2.(2022·浙江·高二开学考试)在平行六面体中,为的中点,为的中点,,则( )
A. B.
C. D.
3.(2022·江苏镇江·高二开学考试)已知四棱锥的底面是平行四边形,侧棱、、上分别有一点、、,且满足,,,若、、、四点共面,则实数__________.
4.(2022·全国·高二课时练习)在空间四点O,A,B,C中,若是空间的一个基底,则下列命题不正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点不共面
D.O,A,B,C四点中任意三点不共线
5.(2022·全国·高二课时练习)已知四面体,所有棱长均为2,点E,F分别为棱AB,CD的中点,则( )
A.1 B.2 C.-1 D.-2
6.(2022·全国·高二专题练习)已知斜三棱柱所有棱长均为2,,点 满足,,则( )
A. B. C.2 D.
7.(2022·全国·高二课时练习)已知空间向量,,满足,,,,则与的夹角为( )
A. B. C. D.
8.(2021·浙江省杭州学军中学高二期中)如图,二面角的大小为,,分别在平面,内,,,,,,则( )
A. B.
C. D.
9.(2022·全国·高二课时练习)已知,.若与的夹角为钝角,则实数的取值范围是________.
培优第二阶——能力提升练
1.(2021·全国·高二课时练习)设且是空间的一组基底,给出下列向量组:
①;② ③ ④
其中可以作为空间的基底的向量组是___________(填序号).
2.(2022·福建·厦门海沧实验中学高二期中)如图,在四面体中,,,,且,,则( )
A. B.
C. D.
3.(2021·福建·厦门双十中学高二期中)已知,若三向量共面,则实数=_____.
4.(2021·河北·石家庄市第十二中学高二期中)下列关于空间向量的说法中,正确的有___________.
①若向量,与空间任意向量都不能构成基底,则
②若非零向量,,满足,,,则有
③是,共线的充分不必要条件
④若,共线,则
5.(2022·全国·高二课时练习)如图,在三棱柱中,底面为正三角形,侧棱垂直于底面,.若E是棱的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
6.(2021·安徽·高二阶段练习)在平行六面体中,,,,,,则AM的长为( )
A. B. C. D.
7.(2022·全国·高二专题练习)已知是棱长为4的正方体内切球的一条直径,点在正方体表面上运动,则的取值范围为( )
A. B. C. D.
8.(2022·河南·洛宁县第一高级中学高二阶段练习)如图,三棱锥各棱的棱长是1,点是棱的中点,点在棱上,且,则的最小值为( )
A. B. C. D.1
9.(2020·浙江·湖州中学模拟预测)已知点是正方体表面上一动点,且满足,设与平面所成的角为,则的最大值为( )
A. B. C. D.
培优第三阶——培优拔尖练
1.(2019·安徽蚌埠·高二期末(理))已知,,,则“”是“,,构成空间的一个基底”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.(2022·云南·罗平县第一中学高二开学考试)如图,平行六面体中,与的交点为,设,,,则选项中与向量相等的是( )
A. B.
C. D.
3.(2022·全国·高二课时练习)在正方体中,点M和N分别是矩形ABCD和的中心,若点P满足,其中,且,则点P可以是正方体表面上的点________.
4.(2022全国·高二专题练习)下列命题正确的是( )
A.若与共线,与线,则与共线
B.向量,,共面,即它们所在的直线共面
C.若∥,则存在唯一的实数λ,使=λ
D.零向量是模为0,方向任意的向量
5.(2022·全国·高二课时练习)如图所示,空间四边形的各边和对角线长均相等,E是BC的中点,那么( ).
A. B.
C. D.与不能比较大小
6.(2022·全国·高二单元测试)如图在平行六面体中,底面 是边长为1的正方形,侧棱且,则 ( )
A. B. C. D.
7.(2021·全国·高二专题练习)已知棱长为的正方体,点在空间直角坐标系的轴上移动,点在平面上移动,则的最大值是( )
A. B. C. D.
8.(2022·全国·高二专题练习)如图,已知正方体的棱长为1,则线段上的动点P到直线的距离的最小值为( )
A.1 B. C. D.
9.(2022·江西鹰潭·高二期末(理))如图,在三棱锥中,,,,点在平面内,且,设异面直线与所成的角为,则的最大值为( )
A. B. C. D.
培优第一阶——基础过关练
1.(2022·全国·高二课时练习)若为空间的一个基底,则下列各组向量中一定能构成空间的一个基底的是______.(填序号)
①,,; ②,,;
③,,; ④,,.
【答案】③
【分析】根据空间向量基本定理判断可得;
【详解】解:由空间向量基本定理得:
对于①,,所以,,三个向量共面;
对于②,,所以,,三个向量共面;
对于③,因为为空间的一个基底,所以与不共线,所以,也不共线,
且与 、共面,与、共面,又、、三个向量不共面,
所以,,不共面,故,,可以作为一组基底;
对于④,,所以,,三个向量共面,
故答案为:③.
2.(2022·浙江·高二开学考试)在平行六面体中,为的中点,为的中点,,则( )
A. B.
C. D.
【答案】C
【分析】设,根据空间向量的线性运算表达,再联立求解即可.
【详解】设则.
所以,,所以.
故选:C
3.(2022·江苏镇江·高二开学考试)已知四棱锥的底面是平行四边形,侧棱、、上分别有一点、、,且满足,,,若、、、四点共面,则实数__________.
【答案】##
【分析】根据四点共面的等价条件以及,可得出关于的两个表达式,可得出关于的方程组,即可解得实数的值.
【详解】因为、、、四点共面,则存在、使得,
所以,,
所以,,
因为,即,所以,,
因为,即,
所以,,可得,解得.故答案为:.
4.(2022·全国·高二课时练习)在空间四点O,A,B,C中,若是空间的一个基底,则下列命题不正确的是( )
A.O,A,B,C四点不共线
B.O,A,B,C四点共面,但不共线
C.O,A,B,C四点不共面
D.O,A,B,C四点中任意三点不共线
【答案】B
【分析】根据基底的含义,非零向量不在同一平面内,即O,A,B,C四点不共面,即可判断
【详解】因为为基底,所以非零向量不在同一平面内,
即O,A,B,C四点不共面,
所以A、C、D选项说法正确,B错误.
故选:B
5.(2022·全国·高二课时练习)已知四面体,所有棱长均为2,点E,F分别为棱AB,CD的中点,则( )
A.1 B.2 C.-1 D.-2
【答案】D
【分析】在四面体中,取定一组基底向量,表示出,,再借助空间向量数量积计算作答.
【详解】四面体的所有棱长均为2,则向量不共面,两两夹角都为,
则,
因点E,F分别为棱AB,CD的中点,则,,
,
所以.
故选:D
6.(2022·全国·高二专题练习)已知斜三棱柱所有棱长均为2,,点 满足,,则( )
A. B. C.2 D.
【答案】D
【分析】以向量为基底向量,则,根据条件由向量的数量积的运算性质,两边平方可得答案.
【详解】以向量为基底向量,
所以 所以 故选:D
7.(2022·全国·高二课时练习)已知空间向量,,满足,,,,则与的夹角为( )
A. B. C. D.
【答案】C
【分析】将,两边平方,利用空间向量的数量积即可得选项.
【详解】设与的夹角为.由,得,两边平方,得,
所以,解得,又,所以,
故选:C.
8.(2021·浙江省杭州学军中学高二期中)如图,二面角的大小为,,分别在平面,内,,,,,,则( )
A. B.
C. D.
【答案】A
【分析】由向量加法可得,再利用向量的模长公式,结合向量数量积公式,化简整理式子即可得到答案.
【详解】,,
与夹角大小为二面角的大小, ,,
又利用向量加法运算知,
,
,即
解得:
故选:A.
9.(2022·全国·高二课时练习)已知,.若与的夹角为钝角,则实数的取值范围是________.
【答案】
【分析】由,,根据与的夹角为钝角,由且求解.
【详解】因为,,所以,
因为与的夹角为钝角,所以且,由,得,
所以.若与的夹角为,则存在,使,即,
所以,解得,故答案为:
培优第二阶——能力提升练
1.(2021·全国·高二课时练习)设且是空间的一组基底,给出下列向量组:
①;② ③ ④
其中可以作为空间的基底的向量组是___________(填序号).
【答案】②③④
【分析】作一个平行六面体,用共点A的三条棱的向量表示已知的基底向量,求出图形中表示的向量,观察图形判断作答.
【详解】如图,平行六面体中,设,
则,,因四点共面,则向量共面,
而四点不共面,则向量不共面,又四点不共面,则不共面,
四点不共面,则也不共面,
所以可以作为空间的基底的向量组是②③④.
故答案为:②③④
2.(2022·福建·厦门海沧实验中学高二期中)如图,在四面体中,,,,且,,则( )
A. B.
C. D.
【答案】C
【分析】由平面向量的线性运算求解.
【详解】连接,因为,所以,因为,所以,
所以.故选:C.
3.(2021·福建·厦门双十中学高二期中)已知,若三向量共面,则实数=_____.
【答案】
【分析】由题意结合向量基本定理得到方程组,求解方程组即可确定的值.
【详解】由题意可知,存在实数满足:,
据此可得方程组:,求解方程组可得:.
故答案为.
4.(2021·河北·石家庄市第十二中学高二期中)下列关于空间向量的说法中,正确的有___________.
①若向量,与空间任意向量都不能构成基底,则
②若非零向量,,满足,,,则有
③是,共线的充分不必要条件
④若,共线,则
【答案】①③
【分析】由空间向量基本定理可判断①;根据空间向量的位置关系可判断②;由向量的数量积以及充分条件和必要条件的定义可判断③;根据共线向量的定义可判断④,进而可得正确答案.
【详解】对于①:若向量,与空间任意向量都不能构成基底,只能两个向量为共线向量,即,故①正确;
对于②:若非零向量,,满足,,,则与不一定共线,故②不正确;
对于③:由可得:
,可得,即,所以,反向共线,故充分性成立,若,共线则,当时,不成立,故是,共线的充分不必要条件,故③正确;
对于④:若,共线,则或与重合,故④不正确;
所以正确的有①③,
故答案为:①③.
5.(2022·全国·高二课时练习)如图,在三棱柱中,底面为正三角形,侧棱垂直于底面,.若E是棱的中点,则异面直线与所成角的余弦值为( )
A. B. C. D.
【答案】A
【分析】以为基底表示出,利用向量夹角公式计算出异面直线与所成角的余弦值.
【详解】设,则构成空间的一个基底,
,,
.所以异面直线与所成角的余弦值为.故选:A
6.(2021·安徽·高二阶段练习)在平行六面体中,,,,,,则AM的长为( )
A. B. C. D.
【答案】C
【分析】由题知,再求向量的模即可得答案.
【详解】解:∵,
∴ ,
∴.
故选:C.
7.(2022·全国·高二专题练习)已知是棱长为4的正方体内切球的一条直径,点在正方体表面上运动,则的取值范围为( )
A. B. C. D.
【答案】C
【分析】利用向量的线性运算和数量积运算可得,根据正方体的特点确定最大值和最小值,即可求解.
【详解】设正方体内切球的球心为,则,
,
因为MN是正方体内切球的一条直径,
所以,,
所以,
又点Р在正方体表面上运动,
所以当为正方体顶点时,最大,且最大值为;
当为内切球与正方体的切点时,最小,且最小值为;
所以,
所以的取值范围为,
故选:C.
8.(2022·河南·洛宁县第一高级中学高二阶段练习)如图,三棱锥各棱的棱长是1,点是棱的中点,点在棱上,且,则的最小值为( )
A. B. C. D.1
【答案】B
【分析】首先在中利用余弦定理求出,然后由空间向量的运算法则可得,变形可得,由二次函数的知识可得答案.
【详解】根据题意,在中, ,所以
所以==
则时,取得最小值,则的最小值为.故选:B
9.(2020·浙江·湖州中学模拟预测)已知点是正方体表面上一动点,且满足,设与平面所成的角为,则的最大值为( )
A. B. C. D.
【答案】A
【分析】建立空间直角坐标系,设出点的坐标,根据已知条件求得动点的轨迹方程,再由直线与平面的夹角可得出最值.
【详解】以为坐标原点,,,所在直线分别为轴,轴,轴建立如图所示的空间直角坐标系,设正方体的边长为2,,则,因为,
所以,即
,所以点的轨迹为以点为球心、为半径的球与正方体表面的交线,
即为如图的,,,要使得与底面所成的角最大,
则与底面的交点到点的距离最短,从而点在上,且在上,
则,从而,所以的最大值为,
故选:A.
培优第三阶——培优拔尖练
1.(2019·安徽蚌埠·高二期末(理))已知,,,则“”是“,,构成空间的一个基底”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
【答案】A
【分析】由共面向量定理可得::当“”时,,易得:,,不共面,即,,能构成空间的一个基底,
当,,能构成空间的一个基底,则,,不共面,解得:,综合得解
【详解】解:当“”时,,
易得:,,不共面,即,,能构成空间的一个基底,
即“”是“,,构成空间的一个基底”的充分条件,
当,,能构成空间的一个基底,则,,不共面,
设,,共面,
即,解得:,即,
即,,能构成空间的一个基底时,m的取值范围为:,
即当,,能构成空间的一个基底,不能推出,
即“”是“,,构成空间的一个基底”的不必要条件
综合得:“”是“,,构成空间的一个基底”的充分不必要条件,
故选A.
2.(2022·云南·罗平县第一中学高二开学考试)如图,平行六面体中,与的交点为,设,,,则选项中与向量相等的是( )
A. B.
C. D.
【答案】A
【分析】根据空间向量线性运算法则计算可得.
【详解】解:平行六面体中,与的交点为,设,,,
所以,
则,
所以.
故选:A.
3.(2022·全国·高二课时练习)在正方体中,点M和N分别是矩形ABCD和的中心,若点P满足,其中,且,则点P可以是正方体表面上的点________.
【答案】(或C或边上的任意一点)
【分析】因为点P满足,其中,且,所以点三点共面,只需要找到平面与正方体表面的交线即可.
【详解】解:因为点P满足,其中,且,
所以点三点共面,
因为点M和N分别是矩形ABCD和的中心,
所以,
连接,则,所以即为经过三点的平面与正方体的截面,
故点P可以是正方体表面上的点(或C或边上的任意一点)
故答案为:(或C或边上的任意一点)
4.(2021·全国·高二专题练习)下列命题正确的是( )
A.若与共线,与线,则与共线
B.向量,,共面,即它们所在的直线共面
C.若∥,则存在唯一的实数λ,使=λ
D.零向量是模为0,方向任意的向量
【答案】D
【分析】假设为零向量,可判断选项A;
根据向量的特征,可判断选项B;
根据向量共线定理,可判断选项C;
根据零向量的定义,可判断选项D.
【详解】由于零向量与任意向量共线,所以若为零向量,则与关系不确定,A错;
因为向量是可以平行移动的,因此向量共面时,它们所在的直线不一定共面,B错;
共线向量定理中,当不是零向量时,才存在唯一的实数λ,使=λ,否则λ可能不存在,C错;
根据零向量的定义可知,零向量的模为0,方向是任意的,D显然正确.
故选:D.
5.(2022·全国·高二课时练习)如图所示,空间四边形的各边和对角线长均相等,E是BC的中点,那么( ).
A. B.
C. D.与不能比较大小
【答案】C
【分析】由题设易得,且,应用向量数量积的运算律化简,进而比较它们的大小关系.
【详解】∵E是BC的中点,,
∴,即.
不妨设空间四边形的各边和对角线长均为1,又,,两两之间的夹角均为60°,
∴.
故.
故选:C
6.(2022·全国·高二单元测试)如图在平行六面体中,底面 是边长为1的正方形,侧棱且,则 ( )
A. B. C. D.
【答案】B
【解析】先求出 ,,,,,,再计算即可.
【详解】解:因为底面是边长为1的正方形,侧棱且,
则 ,,,,,,
则
故选:B.
7.(2021·全国·高二专题练习)已知棱长为的正方体,点在空间直角坐标系的轴上移动,点在平面上移动,则的最大值是( )
A. B. C. D.
【答案】D
【分析】取的中点,连接,求得,取的中点,连接、、、、、,求得,求出的最大值,分析可得,即可求得结果.
【详解】取的中点,连接,如下图所示:
因为平面,平面,则,
因为为的中点且,故,
取的中点,连接、、、、、,如下图所示:
因为为的中点且四边形为正方形,故为的中点,
又因为为的中点,故,
所以,,当且仅当、、三点共线且在线段上时,等号成立,
所以,
.因此,的最大值为.故选:D.
8.(2022·全国·高二专题练习)如图,已知正方体的棱长为1,则线段上的动点P到直线的距离的最小值为( )
A.1 B. C. D.
【答案】D
【分析】利用坐标法,设,可得动点P到直线的距离为,然后利用二次函数的性质即得.
【详解】如图建立空间直角坐标系,则,
设,则,∴动点P到直线的距离为
,当时取等号,
即线段上的动点P到直线的距离的最小值为.故选:D.
9.(2022·江西鹰潭·高二期末(理))如图,在三棱锥中,,,,点在平面内,且,设异面直线与所成的角为,则的最大值为( )
A. B. C. D.
【答案】D
【分析】设线段的中点为,连接,过点在平面内作,垂足为点,证明出平面,然后以点为坐标原点,、、分别为、、轴的正方向建立空间直角坐标系,设,其中,且,求出的最大值,利用空间向量法可求得的最大值.
【详解】设线段的中点为,连接,
,为的中点,则,
,则,,同理可得,,
,平面,
过点在平面内作,垂足为点,
因为,所以,为等边三角形,故为的中点,
平面,平面,则,
,,平面,
以点为坐标原点,、、分别为、、轴的正方向建立如下图所示的空间直角坐标系,
因为是边长为的等边三角形,为的中点,则,
则、、、,由于点在平面内,
可设,
其中,且,从而,
因为,则,所以,,
故当时,有最大值,即,
故,即有最大值,
所以,.故选:D.
