与几何图形有关的二次函数问题[下学期]
文档属性
| 名称 | 与几何图形有关的二次函数问题[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 129.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2008-04-25 14:37:00 | ||
图片预览


文档简介
课件10张PPT。实践与探索
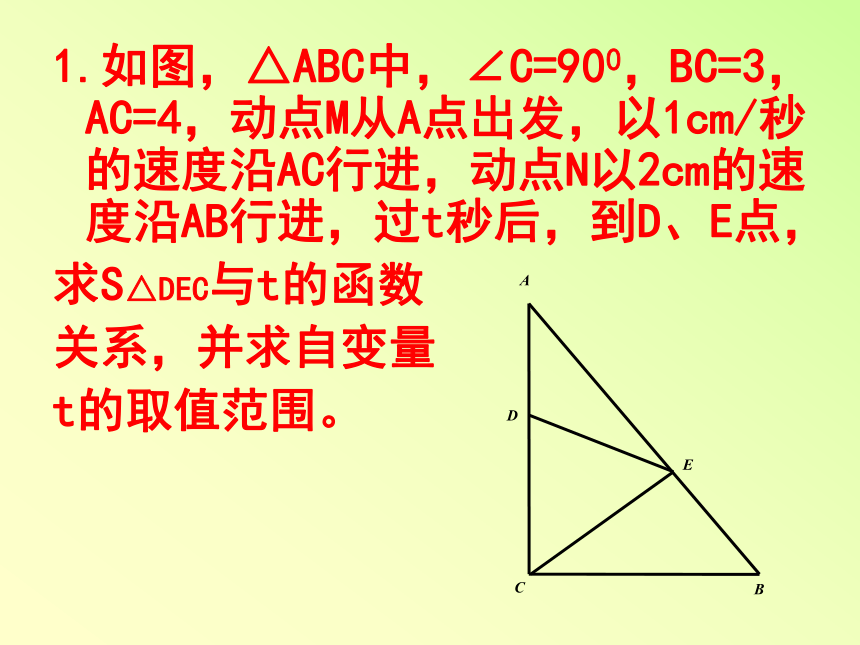
1.如图,△ABC中,∠C=900,BC=3,AC=4,动点M从A点出发,以1cm/秒的速度沿AC行进,动点N以2cm的速度沿AB行进,过t秒后,到D、E点,
求S△DEC与t的函数
关系,并求自变量
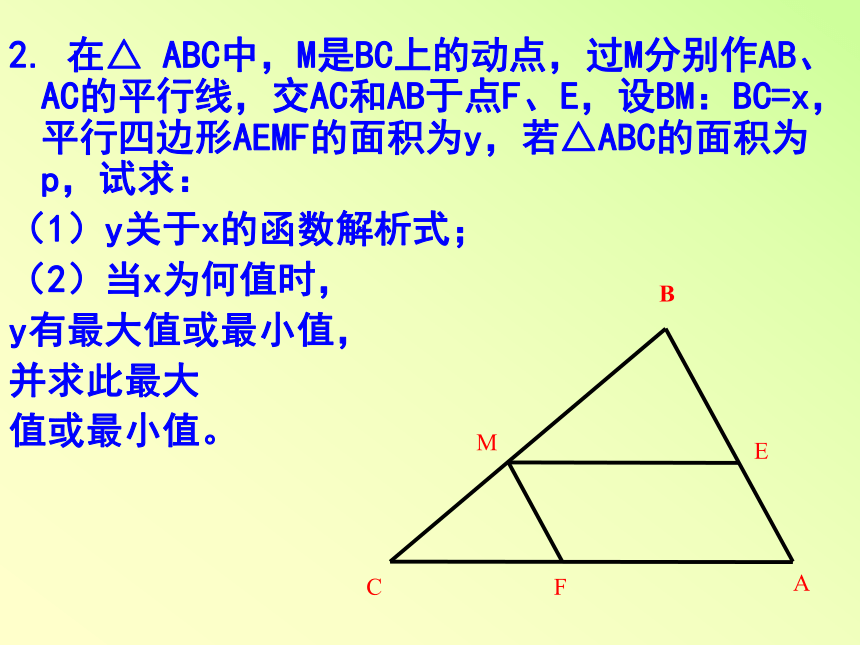
t的取值范围。2. 在△ ABC中,M是BC上的动点,过M分别作AB、AC的平行线,交AC和AB于点F、E,设BM:BC=x,平行四边形AEMF的面积为y,若△ABC的面积为p,试求:
(1)y关于x的函数解析式;
(2)当x为何值时,
y有最大值或最小值,
并求此最大
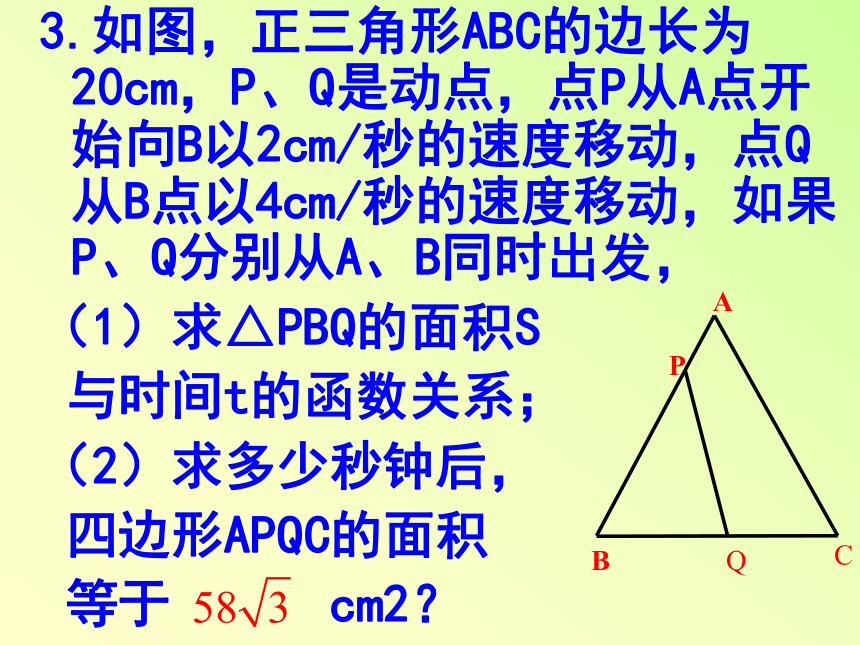
值或最小值。3.如图,正三角形ABC的边长为20cm,P、Q是动点,点P从A点开始向B以2cm/秒的速度移动,点Q从B点以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,
(1)求△PBQ的面积S
与时间t的函数关系;
(2)求多少秒钟后,
四边形APQC的面积
等于 cm2? 4.在△ABC中,∠B=30o,∠C=60o,AC=a.有动点M、N同时从A出发沿三角形的周界运动,M沿ABC方向,N沿ACB方向,运动到两点相遇为止,且N的速度是M的速度的3倍.设AM的长为x,△AMN的面积是y。
(1)当0≤x≤ 时,与当 ≤x≤
时,分别求出y与x的函数关系式。(2)当这两点在什么位置时,△AMN的
面积最大?已知抛物线
(n为常数)。
(1)当抛物线经过直角坐标系的原点,且顶点在第四象限时,求出它的函数关系式;(2) 假设点A是(1)中所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点。过点A作x轴的平行线,交抛物线于另一个点D,再作AB⊥x轴,CD⊥x轴。试问:矩形ABCD的周长是否存在最大值?若存在,请求出;若不存在,请说明理由.为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5︰1。
求:(1)抛物线解析式
中常数c的值;
(2)正方形MNPQ的边长。结束寄语 不知道并不可怕和有害,任何人都不可能什么都知道,可怕的和有害的是不知道而伪装知道.3、如图,矩形ABCD中,AB=1,BC=2,P是AC上的动点,PE与AD相交于E,且∠BPE=900,设CP=x,AE=y,(1)求y与x的函数解析式及自变量x的取值范围;
(2)当AE=PE时,
求四边形ABPE的
面积。
1.如图,△ABC中,∠C=900,BC=3,AC=4,动点M从A点出发,以1cm/秒的速度沿AC行进,动点N以2cm的速度沿AB行进,过t秒后,到D、E点,
求S△DEC与t的函数
关系,并求自变量
t的取值范围。2. 在△ ABC中,M是BC上的动点,过M分别作AB、AC的平行线,交AC和AB于点F、E,设BM:BC=x,平行四边形AEMF的面积为y,若△ABC的面积为p,试求:
(1)y关于x的函数解析式;
(2)当x为何值时,
y有最大值或最小值,
并求此最大
值或最小值。3.如图,正三角形ABC的边长为20cm,P、Q是动点,点P从A点开始向B以2cm/秒的速度移动,点Q从B点以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,
(1)求△PBQ的面积S
与时间t的函数关系;
(2)求多少秒钟后,
四边形APQC的面积
等于 cm2? 4.在△ABC中,∠B=30o,∠C=60o,AC=a.有动点M、N同时从A出发沿三角形的周界运动,M沿ABC方向,N沿ACB方向,运动到两点相遇为止,且N的速度是M的速度的3倍.设AM的长为x,△AMN的面积是y。
(1)当0≤x≤ 时,与当 ≤x≤
时,分别求出y与x的函数关系式。(2)当这两点在什么位置时,△AMN的
面积最大?已知抛物线
(n为常数)。
(1)当抛物线经过直角坐标系的原点,且顶点在第四象限时,求出它的函数关系式;(2) 假设点A是(1)中所确定的抛物线上位于x轴下方、且在对称轴左侧的一个动点。过点A作x轴的平行线,交抛物线于另一个点D,再作AB⊥x轴,CD⊥x轴。试问:矩形ABCD的周长是否存在最大值?若存在,请求出;若不存在,请说明理由.为了参加市科技节展览,同学们制造了一个截面为抛物线形的隧道模型,用了三种正方形的钢筋支架.在画设计图时,如果在直角坐标系中,抛物线的函数解析式为y=-x2+c,正方形ABCD的边长和正方形EFGH的边长之比为5︰1。
求:(1)抛物线解析式
中常数c的值;
(2)正方形MNPQ的边长。结束寄语 不知道并不可怕和有害,任何人都不可能什么都知道,可怕的和有害的是不知道而伪装知道.3、如图,矩形ABCD中,AB=1,BC=2,P是AC上的动点,PE与AD相交于E,且∠BPE=900,设CP=x,AE=y,(1)求y与x的函数解析式及自变量x的取值范围;
(2)当AE=PE时,
求四边形ABPE的
面积。
