备战2023年山东省济南中考数学高频题型靶向集训(二次函数的图象及基本性质)学案(无答案)
文档属性
| 名称 | 备战2023年山东省济南中考数学高频题型靶向集训(二次函数的图象及基本性质)学案(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 246.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 21:47:15 | ||
图片预览


文档简介
备战2023年济南中考数学高频题型靶向集训
(二次函数的图象及基本性质)
题组一:二次函数的概念及表达式
知识储备:
1.二次函数解析式的三种形式
(1)一般式:y=ax2+bx+c(a,b,c为常数,a≠0).
(2)顶点式:y=a(x–h)2+k(a,h,k为常数,a≠0),顶点坐标是(h,k).
(3)交点式:,其中x1,x2是二次函数与x轴的交点的横坐标,a≠0.
过关练习
1.在平面直角坐标系中,将二次函数的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )
A. B. C. D.
2.在平面直角坐标系中,抛物线与轴交于点,则该抛物线关于点成中心对称的抛物线的表达式为( )
A. B.
C. D.
3.如图,抛物线y=a(x﹣2)2+3(a为常数且a≠0)与y轴交于点A(0,).
(1)求该抛物线的解析式;
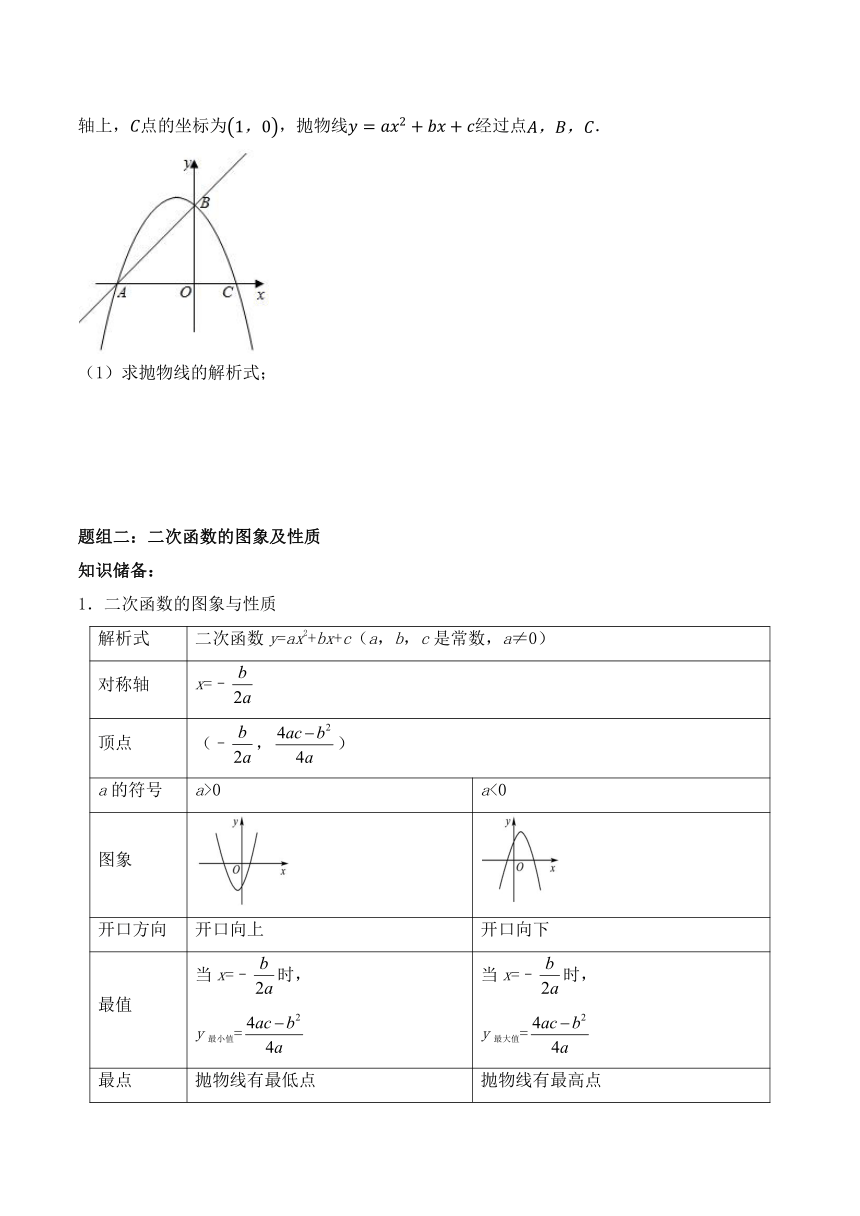
4.如图,在平面直角坐标系中,直线与坐标轴交于两点,点在轴上,点在轴上,点的坐标为,抛物线经过点.
(1)求抛物线的解析式;
题组二:二次函数的图象及性质
知识储备:
1.二次函数的图象与性质
解析式 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)
对称轴 x=–
顶点 (–,)
a的符号 a>0 a<0
图象
开口方向 开口向上 开口向下
最值 当x=–时, y最小值= 当x=–时, y最大值=
最点 抛物线有最低点 抛物线有最高点
增减性 当x<–时,y随x的增大而减小;当x>–时,y随x的增大而增大 当x<–时,y随x的增大而增大;当x>–时,y随x的增大而减小
过关练习
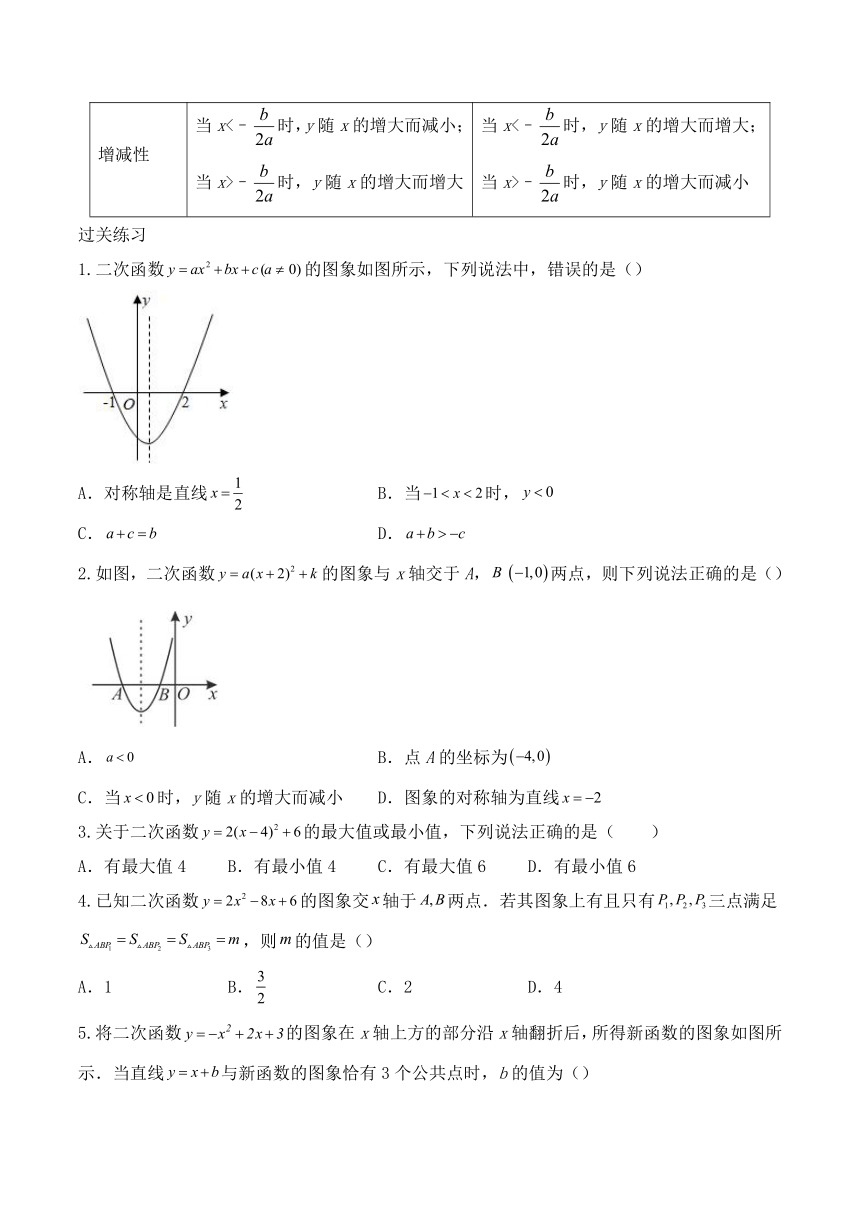
1.二次函数的图象如图所示,下列说法中,错误的是()
A.对称轴是直线 B.当时,
C. D.
2.如图,二次函数的图象与x轴交于A,两点,则下列说法正确的是()
A. B.点A的坐标为
C.当时,y随x的增大而减小 D.图象的对称轴为直线
3.关于二次函数的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
4.已知二次函数的图象交轴于两点.若其图象上有且只有三点满足,则的值是()
A.1 B. C.2 D.4
5.将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为()
A.或 B.或 C.或 D.或
6.设抛物线,其中a为实数.
(1)若抛物线经过点,则______;
(2)将抛物线向上平移2个单位,所得抛物线顶点的纵坐标的最大值是______.
7.如图,在平面直角坐标系中,直线与坐标轴交于两点,点在轴上,点在轴上,点的坐标为,抛物线经过点.
(1)求抛物线的解析式;
(2)根据图象写出不等式的解集;
(3)点是抛物线上的一动点,过点作直线的垂线段,垂足为点,当时,求P点的坐标.
题组三:二次函数图象的特征与a,b,c的关系
知识储备
字母的符号 图象的特征
a a>0 开口向上
a<0 开口向下
b b=0 对称轴为y轴
ab>0(a与b同号) 对称轴在y轴左侧
ab<0(a与b异号) 对称轴在y轴右侧
c c=0 经过原点
c>0 与y轴正半轴相交
c<0 与y轴负半轴相交
b2–4ac b2–4ac=0 与x轴有唯一交点(顶点)
b2–4ac>0 与x轴有两个交点
b2–4ac<0 与x轴没有交点
过关练习
1.已知反比例函数的图象如图所示,则一次函数和二次函数在同一直角坐标系中的图象可能是( )
A.B.C. D.
2.已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c的图象和反比例函数y=的图象在同一坐标系中大致为( )
B.C.D.
3.已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为,且经过点(-1,0).下列结论:①3a+b=0;②若点,(3,y2)是抛物线上的两点,则y1A.1个 B.2个 C.3个 D.4个
4.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其对称轴为直线x=﹣,且与x轴的一个交点坐标为(﹣2,0).下列结论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+c﹣1=0有两个相等的实数根.其中正确结论的序号是( )
A.①③ B.②④ C.③④ D.②③
5.图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )
A.b>0
B.a+b>0
C.x=2是关于x的方程ax2+bx=0(a≠0)的一个根
D.点(x1,y1),(x2,y2)在二次函数的图像上,当x1>x2>2时,y2<y1<0
6.小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图像上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 _____.(填序号,多选、少选、错选都不得分)
7.已知二次函数(是常数,)的与的部分对应值如下表:
0 2
6 0 6
下列结论:
①;
②当时,函数最小值为;
③若点,点在二次函数图象上,则;
④方程有两个不相等的实数根.
其中,正确结论的序号是__________________.(把所有正确结论的序号都填上)
8.如图是抛物线的部分图象,图象过点,对称轴为直线,有下列四个结论:①;②;③y的最大值为3;④方程有实数根.其中正确的为________(将所有正确结论的序号都填入).
(二次函数的图象及基本性质)
题组一:二次函数的概念及表达式
知识储备:
1.二次函数解析式的三种形式
(1)一般式:y=ax2+bx+c(a,b,c为常数,a≠0).
(2)顶点式:y=a(x–h)2+k(a,h,k为常数,a≠0),顶点坐标是(h,k).
(3)交点式:,其中x1,x2是二次函数与x轴的交点的横坐标,a≠0.
过关练习
1.在平面直角坐标系中,将二次函数的图像向左平移2个单位长度,再向上平移1个单位长度,所得抛物线对应的函数表达式为( )
A. B. C. D.
2.在平面直角坐标系中,抛物线与轴交于点,则该抛物线关于点成中心对称的抛物线的表达式为( )
A. B.
C. D.
3.如图,抛物线y=a(x﹣2)2+3(a为常数且a≠0)与y轴交于点A(0,).
(1)求该抛物线的解析式;
4.如图,在平面直角坐标系中,直线与坐标轴交于两点,点在轴上,点在轴上,点的坐标为,抛物线经过点.
(1)求抛物线的解析式;
题组二:二次函数的图象及性质
知识储备:
1.二次函数的图象与性质
解析式 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)
对称轴 x=–
顶点 (–,)
a的符号 a>0 a<0
图象
开口方向 开口向上 开口向下
最值 当x=–时, y最小值= 当x=–时, y最大值=
最点 抛物线有最低点 抛物线有最高点
增减性 当x<–时,y随x的增大而减小;当x>–时,y随x的增大而增大 当x<–时,y随x的增大而增大;当x>–时,y随x的增大而减小
过关练习
1.二次函数的图象如图所示,下列说法中,错误的是()
A.对称轴是直线 B.当时,
C. D.
2.如图,二次函数的图象与x轴交于A,两点,则下列说法正确的是()
A. B.点A的坐标为
C.当时,y随x的增大而减小 D.图象的对称轴为直线
3.关于二次函数的最大值或最小值,下列说法正确的是( )
A.有最大值4 B.有最小值4 C.有最大值6 D.有最小值6
4.已知二次函数的图象交轴于两点.若其图象上有且只有三点满足,则的值是()
A.1 B. C.2 D.4
5.将二次函数的图象在x轴上方的部分沿x轴翻折后,所得新函数的图象如图所示.当直线与新函数的图象恰有3个公共点时,b的值为()
A.或 B.或 C.或 D.或
6.设抛物线,其中a为实数.
(1)若抛物线经过点,则______;
(2)将抛物线向上平移2个单位,所得抛物线顶点的纵坐标的最大值是______.
7.如图,在平面直角坐标系中,直线与坐标轴交于两点,点在轴上,点在轴上,点的坐标为,抛物线经过点.
(1)求抛物线的解析式;
(2)根据图象写出不等式的解集;
(3)点是抛物线上的一动点,过点作直线的垂线段,垂足为点,当时,求P点的坐标.
题组三:二次函数图象的特征与a,b,c的关系
知识储备
字母的符号 图象的特征
a a>0 开口向上
a<0 开口向下
b b=0 对称轴为y轴
ab>0(a与b同号) 对称轴在y轴左侧
ab<0(a与b异号) 对称轴在y轴右侧
c c=0 经过原点
c>0 与y轴正半轴相交
c<0 与y轴负半轴相交
b2–4ac b2–4ac=0 与x轴有唯一交点(顶点)
b2–4ac>0 与x轴有两个交点
b2–4ac<0 与x轴没有交点
过关练习
1.已知反比例函数的图象如图所示,则一次函数和二次函数在同一直角坐标系中的图象可能是( )
A.B.C. D.
2.已知二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c的图象和反比例函数y=的图象在同一坐标系中大致为( )
B.C.D.
3.已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为,且经过点(-1,0).下列结论:①3a+b=0;②若点,(3,y2)是抛物线上的两点,则y1
4.二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,其对称轴为直线x=﹣,且与x轴的一个交点坐标为(﹣2,0).下列结论:①abc>0;②a=b;③2a+c=0;④关于x的一元二次方程ax2+bx+c﹣1=0有两个相等的实数根.其中正确结论的序号是( )
A.①③ B.②④ C.③④ D.②③
5.图,二次函数y=ax2+bx(a≠0)的图像过点(2,0),下列结论错误的是( )
A.b>0
B.a+b>0
C.x=2是关于x的方程ax2+bx=0(a≠0)的一个根
D.点(x1,y1),(x2,y2)在二次函数的图像上,当x1>x2>2时,y2<y1<0
6.小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图像上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 _____.(填序号,多选、少选、错选都不得分)
7.已知二次函数(是常数,)的与的部分对应值如下表:
0 2
6 0 6
下列结论:
①;
②当时,函数最小值为;
③若点,点在二次函数图象上,则;
④方程有两个不相等的实数根.
其中,正确结论的序号是__________________.(把所有正确结论的序号都填上)
8.如图是抛物线的部分图象,图象过点,对称轴为直线,有下列四个结论:①;②;③y的最大值为3;④方程有实数根.其中正确的为________(将所有正确结论的序号都填入).
同课章节目录
