2022—2023学年人教版数学八年级下册 第十七章勾股定理培优同步练习题(含答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册 第十七章勾股定理培优同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 594.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-15 08:02:46 | ||
图片预览

文档简介
第十七章 勾股定理 培优同步练习题
一、单选题
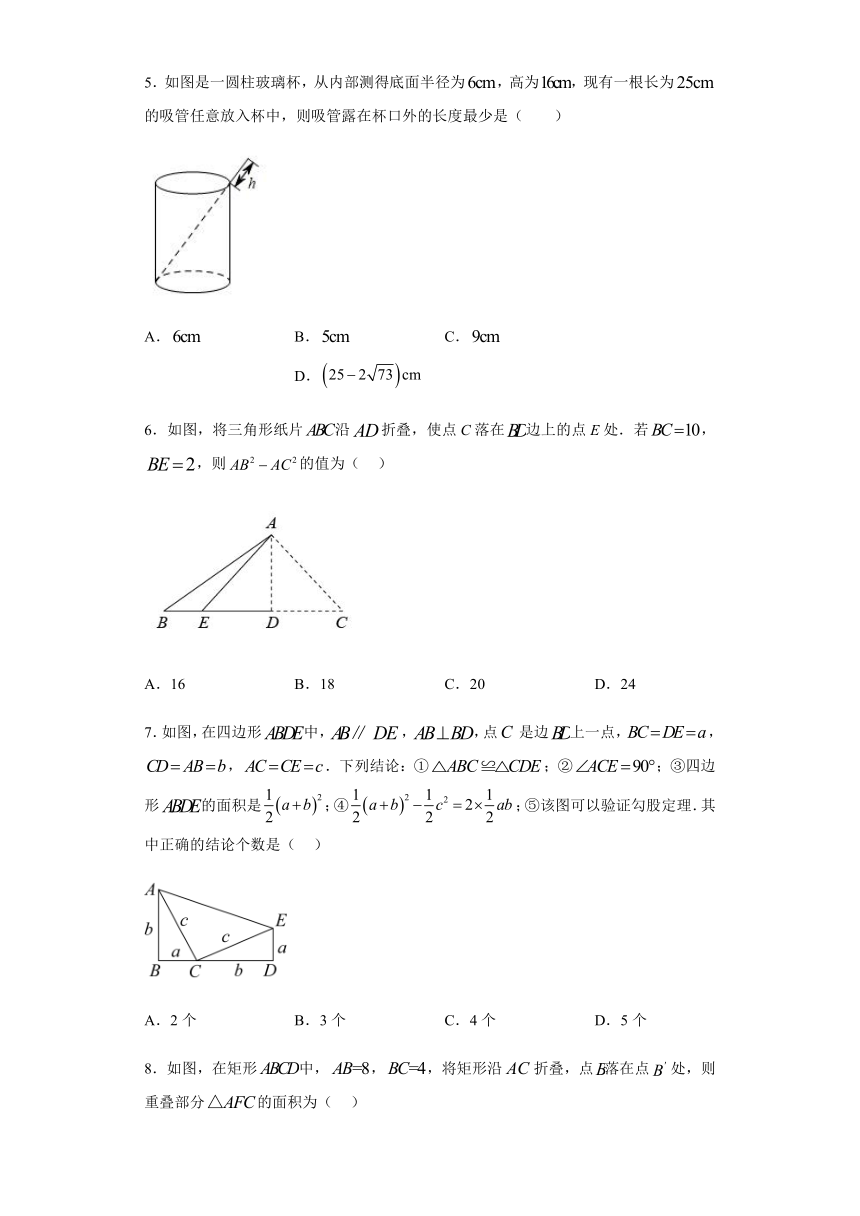
1.如图,边长为x的边等于5的有( )
A.1个 B.2个 C.3个 D.4个
2.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断后垂直地面的竹子高度为尺,则可列方程为( )
A. B.
C. D.
3.如图,在中,,,,线段的垂直平分线交于点P和点Q,则的长度为( )
A.3 B.4 C. D.
4.一架长的梯子斜靠在墙上,梯子底端到墙的距离为.若梯子顶端下滑,那么梯子底端在水平方向上滑动了( )
A. B.小于 C.大于 D.无法确定
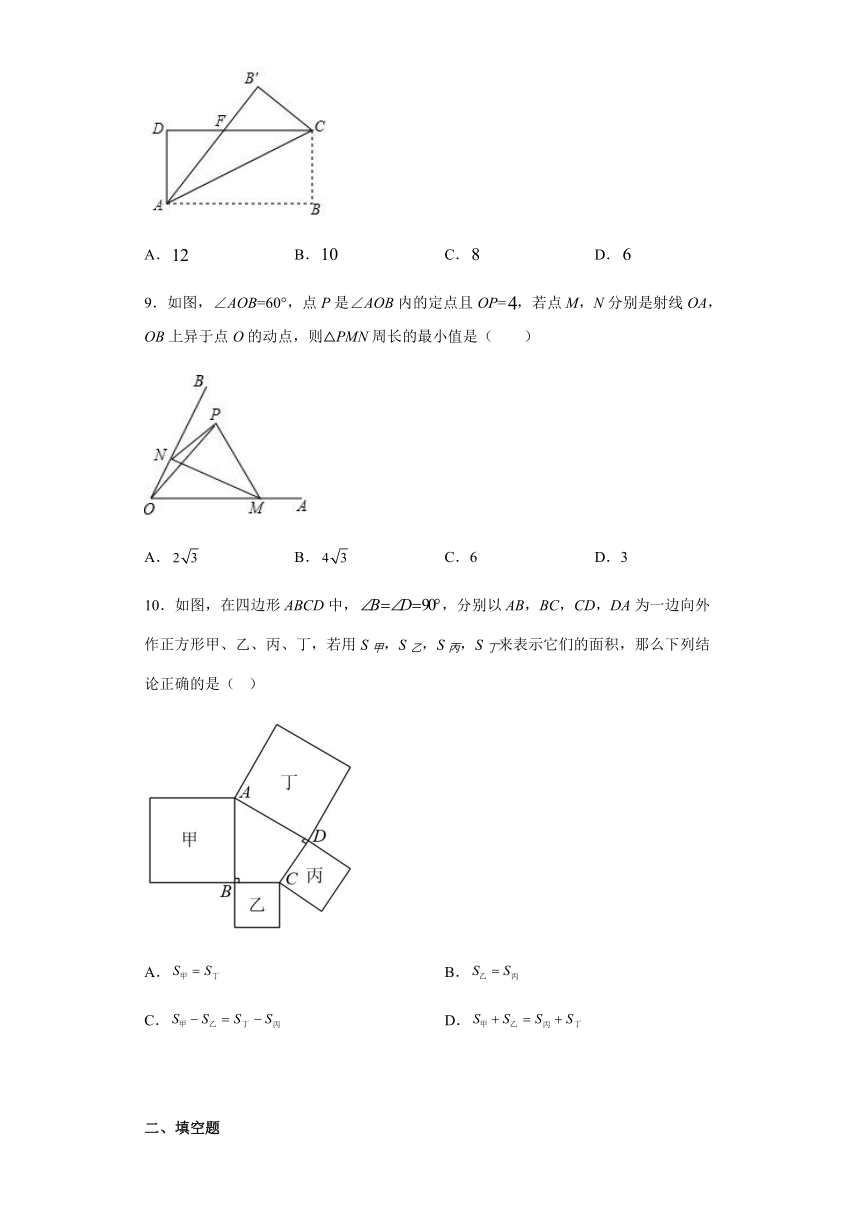
5.如图是一圆柱玻璃杯,从内部测得底面半径为,高为,现有一根长为的吸管任意放入杯中,则吸管露在杯口外的长度最少是( )
A. B. C. D.
6.如图,将三角形纸片沿折叠,使点C落在边上的点E处.若,,则的值为( )
A.16 B.18 C.20 D.24
7.如图,在四边形中,,,点是边上一点,,,.下列结论:①;②;③四边形的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A.2个 B.3个 C.4个 D.5个
8.如图,在矩形中,,,将矩形沿折叠,点落在点处,则重叠部分的面积为( )
A. B. C. D.
9.如图,∠AOB=60°,点P是∠AOB内的定点且OP=,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是( )
A. B. C.6 D.3
10.如图,在四边形ABCD中,,分别以AB,BC,CD,DA为一边向外作正方形甲、乙、丙、丁,若用S甲,S乙,S丙,S丁来表示它们的面积,那么下列结论正确的是( )
A. B.
C. D.
二、填空题
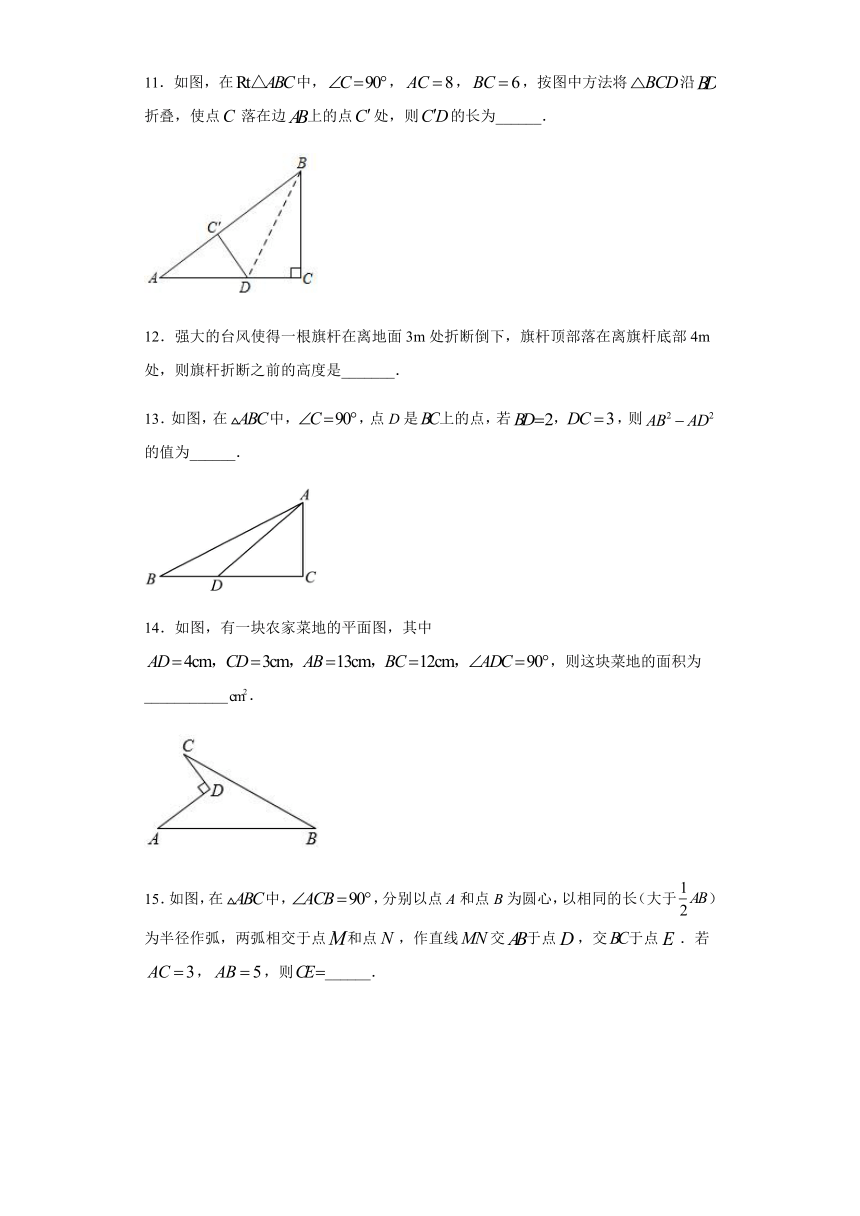
11.如图,在中,,,,按图中方法将沿折叠,使点落在边上的点处,则的长为______.
12.强大的台风使得一根旗杆在离地面3m处折断倒下,旗杆顶部落在离旗杆底部4m处,则旗杆折断之前的高度是_______.
13.如图,在中,,点D是上的点,若,,则的值为______.
14.如图,有一块农家菜地的平面图,其中,则这块菜地的面积为___________.
15.如图,在中,,分别以点A和点B为圆心,以相同的长(大于)为半径作弧,两弧相交于点和点,作直线交于点,交于点.若,,则______.
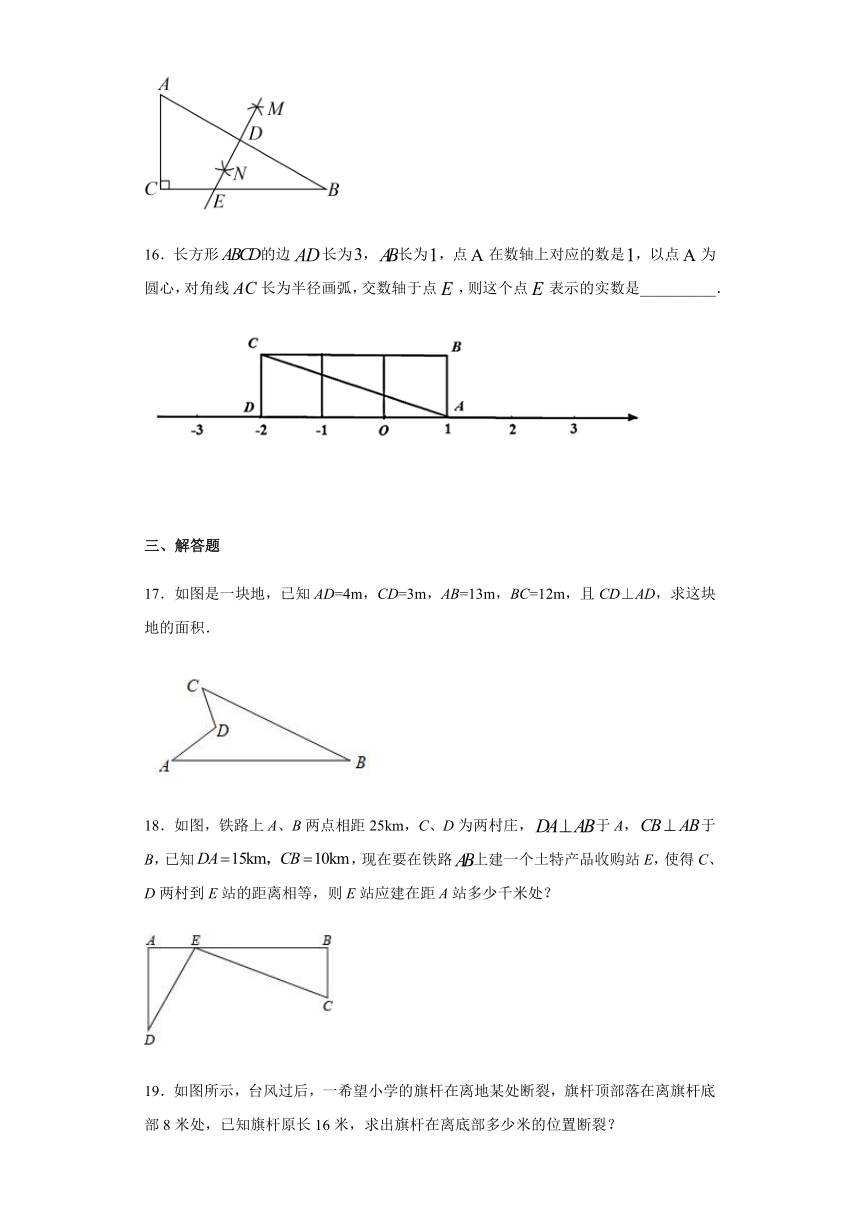
16.长方形的边长为,长为,点在数轴上对应的数是,以点为圆心,对角线长为半径画弧,交数轴于点,则这个点表示的实数是__________.
三、解答题
17.如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
18.如图,铁路上A、B两点相距25km,C、D为两村庄,于A,于B,已知,现在要在铁路上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
19.如图所示,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆原长16米,求出旗杆在离底部多少米的位置断裂?
20.如图,有一块直角三角形纸片,两直角边,,现将直角边沿直线折叠,使它恰好落在斜边上,且与重合,求的长.
21.如图,一个牧童在小河的南4华里(长度单位)的A处牧马,而他正位于他的小屋B的西8华里北7华里处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少
22.如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
23.有一只小鸟在一棵高4m的小树梢上捉虫子,它的伙伴在离该树12m,高20m的一棵大树的树梢上发出友好的叫声,它立刻以4m/s的速度飞向大树树梢,那么这只小鸟至少几秒才可能到达大树和伙伴在一起?
24.麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.
(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
25.如图,在中,,,AD是的角平分线,,垂足为E.
求证:;
已知,求AC的长;
求证:.
参考答案:
1.B
2.C
3.D
4.A
5.B
6.C
7.D
8.B
9.B
10.D
11.3
12.8m
13.16
14.
15.
16.或,
17.解:连接,
∵
∴,
∵,
∴,
又∵,
∴,
又∵,
∴,
又∵,
∴,
∴,
∴.
18.解:设,
∵C、D两村到E站的距离相等,
∴,即,
由勾股定理,得,
∴,
解得.
∴E点应建在距A站10千米处.
19.解:在Rt△ABC中,C=90 ,BC=8米
设AC=x米,则AB=(16 – x )米
∵
即
解得x = 6
答:旗杆在离底部6米的位置断裂.
20.解:∵在中,两直角边,
,
由折叠的性质可知:,
,
设cm,则,
在中,由勾股定理得:,
即,
解得:.
即cm.
21.解:作出A点关于MN的对称点,连接交MN于点P,则就是最短路线,如图所示:
,,,
∵MN垂直平分,
∴,
∵在中,,
∴,
∴(华里).
答:牧童所走的最短里程是17华里.
22.解 连接BD,
在Rt△BAD中,
∵AB=AD=2,
∴∠ADB=45°,BD==2,
在△BCD中,
DB2+CD2=(2)2+12=9=CB2,
∴△BCD是直角三角形,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=45°+90°=135°.
故答案为135°.
23.
如图
,,
根据勾股定理,得,
则小鸟所用的时间是.
答:这只小鸟至少5秒才可能到达小树和伙伴在一起.
24.如图,连接AC,
在Rt△ABC中,AC2=AB2+BC2=32+42=52,
∴AC=5m.
在△ACD中,CD2=132,AD2=122,
而122+52=132,
即AC2+AD2=CD2,
∴∠CAD=90°,
S四边形ABCD=S△BAC+S△DAC= BC AB+AD AC=×4×3+×12×5=36(m2).
答:空地ABCD的面积为36m2.
(2)所以需费用为:36×300=10800(元).
答:总共需投入10800元.
25.证明:在中,,,
是等腰直角三角形,
,
,
是等腰直角三角形,
.
是的角平分线,
,
;
解:由知,是等腰直角三角形,,
,
,
;
证明:是的角平分线,,
.
在与中,
,
≌,
.
由知,
.
一、单选题
1.如图,边长为x的边等于5的有( )
A.1个 B.2个 C.3个 D.4个
2.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断后垂直地面的竹子高度为尺,则可列方程为( )
A. B.
C. D.
3.如图,在中,,,,线段的垂直平分线交于点P和点Q,则的长度为( )
A.3 B.4 C. D.
4.一架长的梯子斜靠在墙上,梯子底端到墙的距离为.若梯子顶端下滑,那么梯子底端在水平方向上滑动了( )
A. B.小于 C.大于 D.无法确定
5.如图是一圆柱玻璃杯,从内部测得底面半径为,高为,现有一根长为的吸管任意放入杯中,则吸管露在杯口外的长度最少是( )
A. B. C. D.
6.如图,将三角形纸片沿折叠,使点C落在边上的点E处.若,,则的值为( )
A.16 B.18 C.20 D.24
7.如图,在四边形中,,,点是边上一点,,,.下列结论:①;②;③四边形的面积是;④;⑤该图可以验证勾股定理.其中正确的结论个数是( )
A.2个 B.3个 C.4个 D.5个
8.如图,在矩形中,,,将矩形沿折叠,点落在点处,则重叠部分的面积为( )
A. B. C. D.
9.如图,∠AOB=60°,点P是∠AOB内的定点且OP=,若点M,N分别是射线OA,OB上异于点O的动点,则△PMN周长的最小值是( )
A. B. C.6 D.3
10.如图,在四边形ABCD中,,分别以AB,BC,CD,DA为一边向外作正方形甲、乙、丙、丁,若用S甲,S乙,S丙,S丁来表示它们的面积,那么下列结论正确的是( )
A. B.
C. D.
二、填空题
11.如图,在中,,,,按图中方法将沿折叠,使点落在边上的点处,则的长为______.
12.强大的台风使得一根旗杆在离地面3m处折断倒下,旗杆顶部落在离旗杆底部4m处,则旗杆折断之前的高度是_______.
13.如图,在中,,点D是上的点,若,,则的值为______.
14.如图,有一块农家菜地的平面图,其中,则这块菜地的面积为___________.
15.如图,在中,,分别以点A和点B为圆心,以相同的长(大于)为半径作弧,两弧相交于点和点,作直线交于点,交于点.若,,则______.
16.长方形的边长为,长为,点在数轴上对应的数是,以点为圆心,对角线长为半径画弧,交数轴于点,则这个点表示的实数是__________.
三、解答题
17.如图是一块地,已知AD=4m,CD=3m,AB=13m,BC=12m,且CD⊥AD,求这块地的面积.
18.如图,铁路上A、B两点相距25km,C、D为两村庄,于A,于B,已知,现在要在铁路上建一个土特产品收购站E,使得C、D两村到E站的距离相等,则E站应建在距A站多少千米处?
19.如图所示,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8米处,已知旗杆原长16米,求出旗杆在离底部多少米的位置断裂?
20.如图,有一块直角三角形纸片,两直角边,,现将直角边沿直线折叠,使它恰好落在斜边上,且与重合,求的长.
21.如图,一个牧童在小河的南4华里(长度单位)的A处牧马,而他正位于他的小屋B的西8华里北7华里处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少
22.如图,四边形ABCD,AB=AD=2,BC=3,CD=1,∠A=90°,求∠ADC的度数.
23.有一只小鸟在一棵高4m的小树梢上捉虫子,它的伙伴在离该树12m,高20m的一棵大树的树梢上发出友好的叫声,它立刻以4m/s的速度飞向大树树梢,那么这只小鸟至少几秒才可能到达大树和伙伴在一起?
24.麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.
(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
25.如图,在中,,,AD是的角平分线,,垂足为E.
求证:;
已知,求AC的长;
求证:.
参考答案:
1.B
2.C
3.D
4.A
5.B
6.C
7.D
8.B
9.B
10.D
11.3
12.8m
13.16
14.
15.
16.或,
17.解:连接,
∵
∴,
∵,
∴,
又∵,
∴,
又∵,
∴,
又∵,
∴,
∴,
∴.
18.解:设,
∵C、D两村到E站的距离相等,
∴,即,
由勾股定理,得,
∴,
解得.
∴E点应建在距A站10千米处.
19.解:在Rt△ABC中,C=90 ,BC=8米
设AC=x米,则AB=(16 – x )米
∵
即
解得x = 6
答:旗杆在离底部6米的位置断裂.
20.解:∵在中,两直角边,
,
由折叠的性质可知:,
,
设cm,则,
在中,由勾股定理得:,
即,
解得:.
即cm.
21.解:作出A点关于MN的对称点,连接交MN于点P,则就是最短路线,如图所示:
,,,
∵MN垂直平分,
∴,
∵在中,,
∴,
∴(华里).
答:牧童所走的最短里程是17华里.
22.解 连接BD,
在Rt△BAD中,
∵AB=AD=2,
∴∠ADB=45°,BD==2,
在△BCD中,
DB2+CD2=(2)2+12=9=CB2,
∴△BCD是直角三角形,
∴∠BDC=90°,
∴∠ADC=∠ADB+∠BDC=45°+90°=135°.
故答案为135°.
23.
如图
,,
根据勾股定理,得,
则小鸟所用的时间是.
答:这只小鸟至少5秒才可能到达小树和伙伴在一起.
24.如图,连接AC,
在Rt△ABC中,AC2=AB2+BC2=32+42=52,
∴AC=5m.
在△ACD中,CD2=132,AD2=122,
而122+52=132,
即AC2+AD2=CD2,
∴∠CAD=90°,
S四边形ABCD=S△BAC+S△DAC= BC AB+AD AC=×4×3+×12×5=36(m2).
答:空地ABCD的面积为36m2.
(2)所以需费用为:36×300=10800(元).
答:总共需投入10800元.
25.证明:在中,,,
是等腰直角三角形,
,
,
是等腰直角三角形,
.
是的角平分线,
,
;
解:由知,是等腰直角三角形,,
,
,
;
证明:是的角平分线,,
.
在与中,
,
≌,
.
由知,
.
