二次函数(一)[下学期]
图片预览





文档简介
课件21张PPT。二次函数(一)一、中考要点分析1、一般地,y=ax2+bx+c(a,b,c是常数,a≠0)称为y是x的二次函数,它的图像是抛物线. ?
2.抛物线y=ax2+bx+c的特征与a、b、c的符号:
(1)a决定开口方向:
(2)a与b决定对称轴位置:
3. 抛物线与x轴交点个数的判定.
(1)b2-4ac>0 2个交点.
(2)b2-4ac = 0 1个交点.
(3)b2-4ac<0 0个.(3) c决定抛物线与y轴交点位置y=ax2+bx+c(a≠0)4.常用的二次函数解析式的求法:
(1)一般式:y=ax2+bx+c
(2)顶点式:y=a(x-m)2+n
(3)交点式:y=a(x-x1)(x-x2)
5.二次函数y=ax2+bx+c的对称轴为x=-b/2a,最值为y= ,要善于利用图像的对称性,同时抓住抛物线的顶点、与x轴的交点,与y轴的交点这几个关键点来解决有关的问题。
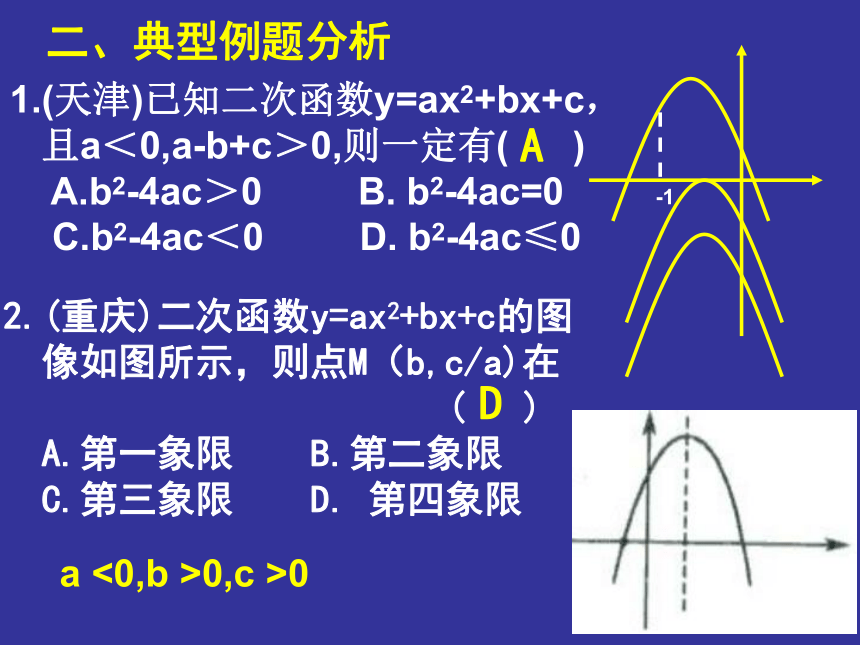
1.(天津)已知二次函数y=ax2+bx+c,
且a<0,a-b+c>0,则一定有( )
A.b2-4ac>0 B. b2-4ac=0
C.b2-4ac<0 D. b2-4ac≤0二、典型例题分析A2.(重庆)二次函数y=ax2+bx+c的图
像如图所示,则点M(b,c/a)在
( )
A.第一象限 B.第二象限
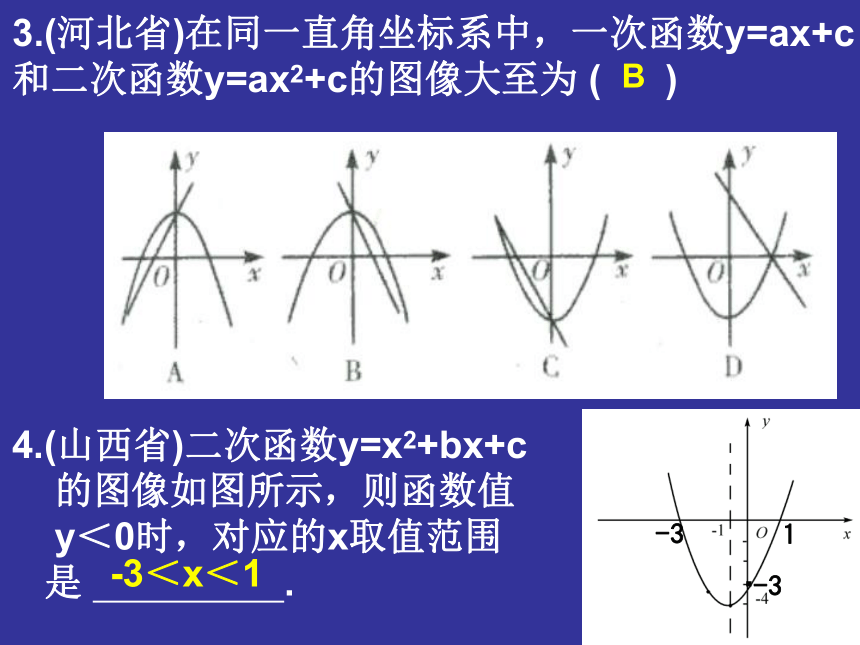
C.第三象限 D. 第四象限D-1a <0,b >0,c >03.(河北省)在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图像大至为 ( )B4.(山西省)二次函数y=x2+bx+c
的图像如图所示,则函数值
y<0时,对应的x取值范围
是 .-3<x<1.-3-315、已知二次函数y=ax2+bx+c的
图像如图所示,下列结论:
① a+b+c<0,②a-b+c>0;
③ abc>0;④b=2a
中正确个数为 ( )
A.4个 B.3个
C.2个 D.1个A6、无论m为任何实数,二次函数y=x2-(2-m)x+m
的图像总是过点 ( )
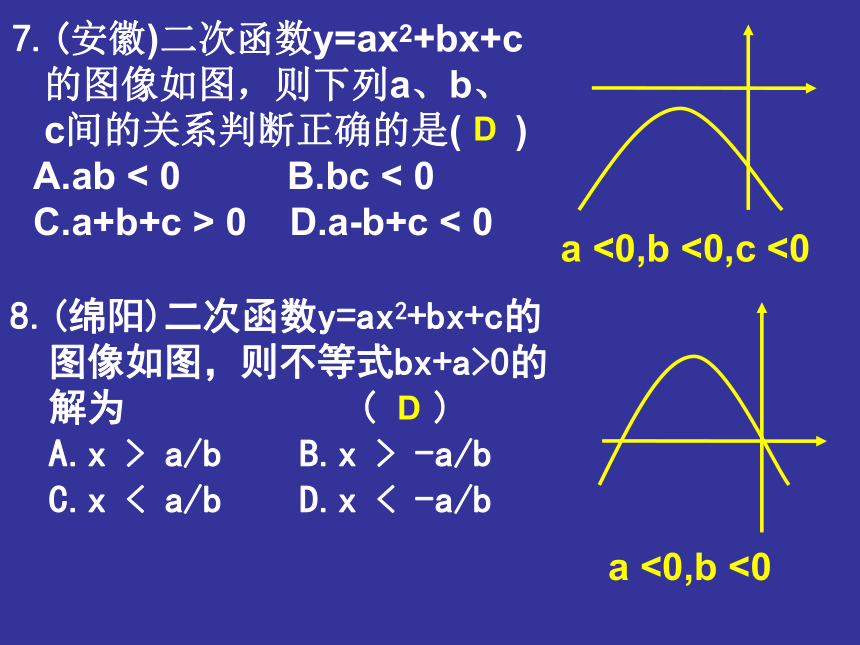
A.(1,3) B.(1,0) C.(-1,3) D.(-1,0)C当x= 1时,y=a+b+c当x=-1时,y=a-b+ca <0,b <0,c>0x=- b/2a=-1D7.(安徽)二次函数y=ax2+bx+c
的图像如图,则下列a、b、
c间的关系判断正确的是( )
A.ab < 0 B.bc < 0
C.a+b+c > 0 D.a-b+c < 0 8.(绵阳)二次函数y=ax2+bx+c的
图像如图,则不等式bx+a>0的
解为 ( )
A.x > a/b B.x > -a/b
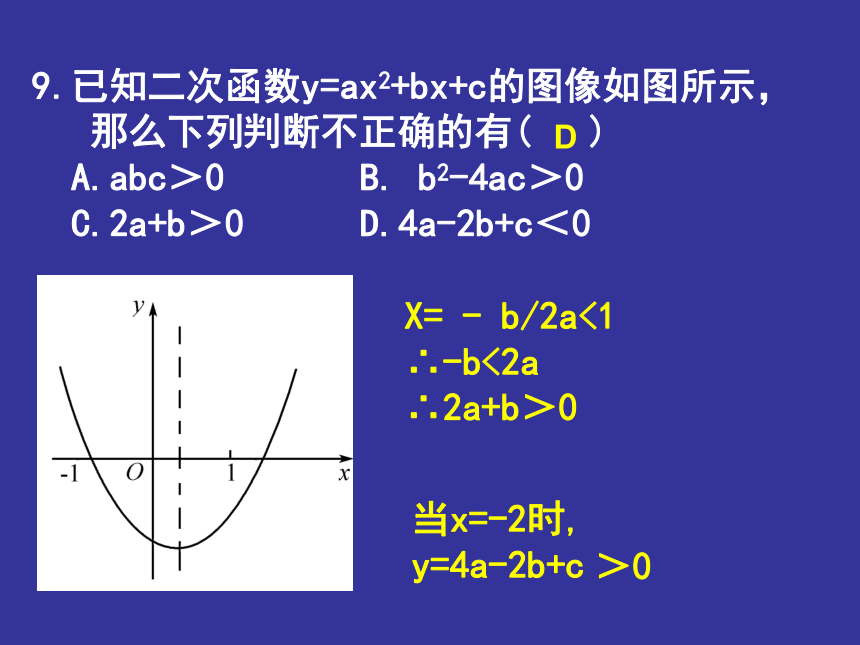
C.x < a/b D.x < -a/b Da <0,b <0,c <0a <0,b <09.已知二次函数y=ax2+bx+c的图像如图所示,
那么下列判断不正确的有( )
A.abc>0 B. b2-4ac>0
C.2a+b>0 D.4a-2b+c<0
DX= - b/2a<1
∴-b<2a
∴2a+b>0 当x=-2时,
y=4a-2b+c>0D10、若抛物线y=ax2+3x+1与x轴有两
个交点,则a的取值范围是( )
A.a>0 B.a>- 4/9
C.a> 9/4 D.a<9/4且a≠0抛物线y=ax2+bx+c与x轴交点个数问题与一元二次方程ax2+bx+c=0的根的个数问题紧密联系.11.某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水呈抛物线状(抛物线所在平面与墙面垂直,如图所示).如果抛物线的最高点M离墙1米,离地面403米,则水流落地点B离墙的距离OB是 ( )
A.2米 B.3米
C.4米 D.5米BO①抛物线顶点M(1,403)
与y轴交点A(0.10) ②求得抛物线解析式;③求出抛物线与x轴的交点;1、(青海省)如图所示,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4,x1x2=3,
(1)求此抛物线的解析式;
(2)设此抛物线与y轴的交点为C,过点B、C作直线,求此直线的解析式;
(3)求△ABC的面积.
(1)y= -x2+4x-3 (2) y= x-3 (3) 3 三、综合应用 能力提升2、已知:二次函数y=2x2-(m+1)x+(m-1).
(1)求证:不论m为何值时,函数的图像与x轴总有交点,并指出m为何值时,只有一个交点;
(2)当m为何值时,函数图像过原点,并指出此时函数图像与x轴的另一个交点;
(3)若函数图像的顶点在第四象限,求m的取值范围.
(2)另一个交点坐标为(1,0) (3)当m>-1且m≠3时,抛物线的顶点在第四象限 3、如图所示,已知抛物线y=ax2+bx+c与x轴负半轴交于A、B两点,与y轴交于点C,且OB= ,CB=2 ,∠CAO=30°,求抛物线的解析式和它的顶点坐标. OA= 3OC= 34、(杭州市)如图所示,在矩形ABCD中, BD=20,AD>AB,设∠ABD=α,已知sinα是方程25x2-35x+12=0的一个实根,点E、F分别是BC,DC上的点,EC+CF=8,设BE=x,△AEF的面积等于y;
(1)求y与x之间的函数关系式;
(2)当E、F两点在什么位置时,
y有最小值?并求出这个最小值. ⑤当x=10时,即BE=10,CF=2时,
y有最小值为46 ①由方程的解及题设中AD>AB,
得sinα= 4/5,求出AD=16.AB=12;分析:③ y= S矩形ABCD-S△AEB-S△CEF-S△ADF④②分别表示出各三角形的各边长;5、 (陕西省)如图所示的直角
坐标系中,以点A ( , 0 )为圆心,
以 为半径的圆与x轴交于B、C
两点,与y轴交于D、E两点.
(1)求D点的坐标;
(2)若B、C、D三点在抛物线y=ax2+bx+c上,求这个抛物线的解析式;
(3)若⊙A的切线交x轴正半轴于点M,交y轴负半轴于点N,切点为P,且∠OMN=30°,试判断直线MN是否经过所求抛物线顶点?说明理由. D的坐标为(0,-3) 抛物线的顶点在直线MN上. 6、如图,抛物线 与y轴交于点C,与直线
y=x相交与A、B两点,且AC∥x轴,OA=OB ; (1)求p、q的值;
(2)若长度为 线段DE在线段AB上移动 ,过点D作y轴的平行线,交抛物线于点F,点D的横坐标为t, △ DEF的面积为S,试把S表示
成t的函数,并求出自变量t的取
值范围和S的最大值;( 1)作BD⊥y 轴于DD∵OA=OB , ∠ AOC= ∠ BOD∵ AC∥x轴 , x轴 ⊥y 轴 ∴ AC ⊥y 轴
又∵ BD⊥y 轴 ∴ ∠BDO= ∠ACO∴BD=AC,OD=CO∵C(0,q),AC ∥ x轴∴点A的纵坐标为q。∵A在直线y=x上∴A(q,q)∴B(- q,- q)由①、②,且q≠0∴△ACO≌ △BDOAC∥x轴, OA=OB解:也可利用对称性得!DH分析: 1、要求S,应以哪一条线段为底?哪一条线段为高线?3、如何表示出高线?2、如何表示出底边?(别忘了点D的横坐标为t!且DF∥y 轴)(ΔDEH为什么三角形?)解:∵DF ∥y 轴, D的横坐标为t∴F的横坐标也为t∴ HD=HE=1∵ A(q,q)即(-2,-2)∴AC=OC=2∴∠AOC=45o∵DF ∥y 轴 ∴ ∠HDE= ∠AOC=45o又∵DE=易得- 2≤t ≤1,t=0时,S最大=1单位21- 21.二次函数的图象有着丰富的内涵,解决二次函数的题目应尽可能地画出大致的抛物线图象,结合图形,解决问题.利用a、b、c的值可判断二次函数的大致位置情况;反之,若已知二次函数的大致位置,也可以判断出一些特殊关系式或字母的取值范围等.
2.二次函数还与一元二次方程的知识紧密联系.利用方程根的性质、根的判别式,可判定抛物线与x轴交点的情况;反之,可以求某些字母的取值范围. 四、方法小结3.要准确辨析条件,选用适当的形式求二次函数解析式,即已知任意三点坐标选用一般式;已知顶点坐标、对称轴或最值常可选用顶点式;已知抛物线与x轴的两个交点坐标常选用交点式.
2.抛物线y=ax2+bx+c的特征与a、b、c的符号:
(1)a决定开口方向:
(2)a与b决定对称轴位置:
3. 抛物线与x轴交点个数的判定.
(1)b2-4ac>0 2个交点.
(2)b2-4ac = 0 1个交点.
(3)b2-4ac<0 0个.(3) c决定抛物线与y轴交点位置y=ax2+bx+c(a≠0)4.常用的二次函数解析式的求法:
(1)一般式:y=ax2+bx+c
(2)顶点式:y=a(x-m)2+n
(3)交点式:y=a(x-x1)(x-x2)
5.二次函数y=ax2+bx+c的对称轴为x=-b/2a,最值为y= ,要善于利用图像的对称性,同时抓住抛物线的顶点、与x轴的交点,与y轴的交点这几个关键点来解决有关的问题。
1.(天津)已知二次函数y=ax2+bx+c,
且a<0,a-b+c>0,则一定有( )
A.b2-4ac>0 B. b2-4ac=0
C.b2-4ac<0 D. b2-4ac≤0二、典型例题分析A2.(重庆)二次函数y=ax2+bx+c的图
像如图所示,则点M(b,c/a)在
( )
A.第一象限 B.第二象限
C.第三象限 D. 第四象限D-1a <0,b >0,c >03.(河北省)在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图像大至为 ( )B4.(山西省)二次函数y=x2+bx+c
的图像如图所示,则函数值
y<0时,对应的x取值范围
是 .-3<x<1.-3-315、已知二次函数y=ax2+bx+c的
图像如图所示,下列结论:
① a+b+c<0,②a-b+c>0;
③ abc>0;④b=2a
中正确个数为 ( )
A.4个 B.3个
C.2个 D.1个A6、无论m为任何实数,二次函数y=x2-(2-m)x+m
的图像总是过点 ( )
A.(1,3) B.(1,0) C.(-1,3) D.(-1,0)C当x= 1时,y=a+b+c当x=-1时,y=a-b+ca <0,b <0,c>0x=- b/2a=-1D7.(安徽)二次函数y=ax2+bx+c
的图像如图,则下列a、b、
c间的关系判断正确的是( )
A.ab < 0 B.bc < 0
C.a+b+c > 0 D.a-b+c < 0 8.(绵阳)二次函数y=ax2+bx+c的
图像如图,则不等式bx+a>0的
解为 ( )
A.x > a/b B.x > -a/b
C.x < a/b D.x < -a/b Da <0,b <0,c <0a <0,b <09.已知二次函数y=ax2+bx+c的图像如图所示,
那么下列判断不正确的有( )
A.abc>0 B. b2-4ac>0
C.2a+b>0 D.4a-2b+c<0
DX= - b/2a<1
∴-b<2a
∴2a+b>0 当x=-2时,
y=4a-2b+c>0D10、若抛物线y=ax2+3x+1与x轴有两
个交点,则a的取值范围是( )
A.a>0 B.a>- 4/9
C.a> 9/4 D.a<9/4且a≠0抛物线y=ax2+bx+c与x轴交点个数问题与一元二次方程ax2+bx+c=0的根的个数问题紧密联系.11.某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水呈抛物线状(抛物线所在平面与墙面垂直,如图所示).如果抛物线的最高点M离墙1米,离地面403米,则水流落地点B离墙的距离OB是 ( )
A.2米 B.3米
C.4米 D.5米BO①抛物线顶点M(1,403)
与y轴交点A(0.10) ②求得抛物线解析式;③求出抛物线与x轴的交点;1、(青海省)如图所示,已知抛物线y=-x2+bx+c与x轴的两个交点分别为A(x1,0),B(x2,0),且x1+x2=4,x1x2=3,
(1)求此抛物线的解析式;
(2)设此抛物线与y轴的交点为C,过点B、C作直线,求此直线的解析式;
(3)求△ABC的面积.
(1)y= -x2+4x-3 (2) y= x-3 (3) 3 三、综合应用 能力提升2、已知:二次函数y=2x2-(m+1)x+(m-1).
(1)求证:不论m为何值时,函数的图像与x轴总有交点,并指出m为何值时,只有一个交点;
(2)当m为何值时,函数图像过原点,并指出此时函数图像与x轴的另一个交点;
(3)若函数图像的顶点在第四象限,求m的取值范围.
(2)另一个交点坐标为(1,0) (3)当m>-1且m≠3时,抛物线的顶点在第四象限 3、如图所示,已知抛物线y=ax2+bx+c与x轴负半轴交于A、B两点,与y轴交于点C,且OB= ,CB=2 ,∠CAO=30°,求抛物线的解析式和它的顶点坐标. OA= 3OC= 34、(杭州市)如图所示,在矩形ABCD中, BD=20,AD>AB,设∠ABD=α,已知sinα是方程25x2-35x+12=0的一个实根,点E、F分别是BC,DC上的点,EC+CF=8,设BE=x,△AEF的面积等于y;
(1)求y与x之间的函数关系式;
(2)当E、F两点在什么位置时,
y有最小值?并求出这个最小值. ⑤当x=10时,即BE=10,CF=2时,
y有最小值为46 ①由方程的解及题设中AD>AB,
得sinα= 4/5,求出AD=16.AB=12;分析:③ y= S矩形ABCD-S△AEB-S△CEF-S△ADF④②分别表示出各三角形的各边长;5、 (陕西省)如图所示的直角
坐标系中,以点A ( , 0 )为圆心,
以 为半径的圆与x轴交于B、C
两点,与y轴交于D、E两点.
(1)求D点的坐标;
(2)若B、C、D三点在抛物线y=ax2+bx+c上,求这个抛物线的解析式;
(3)若⊙A的切线交x轴正半轴于点M,交y轴负半轴于点N,切点为P,且∠OMN=30°,试判断直线MN是否经过所求抛物线顶点?说明理由. D的坐标为(0,-3) 抛物线的顶点在直线MN上. 6、如图,抛物线 与y轴交于点C,与直线
y=x相交与A、B两点,且AC∥x轴,OA=OB ; (1)求p、q的值;
(2)若长度为 线段DE在线段AB上移动 ,过点D作y轴的平行线,交抛物线于点F,点D的横坐标为t, △ DEF的面积为S,试把S表示
成t的函数,并求出自变量t的取
值范围和S的最大值;( 1)作BD⊥y 轴于DD∵OA=OB , ∠ AOC= ∠ BOD∵ AC∥x轴 , x轴 ⊥y 轴 ∴ AC ⊥y 轴
又∵ BD⊥y 轴 ∴ ∠BDO= ∠ACO∴BD=AC,OD=CO∵C(0,q),AC ∥ x轴∴点A的纵坐标为q。∵A在直线y=x上∴A(q,q)∴B(- q,- q)由①、②,且q≠0∴△ACO≌ △BDOAC∥x轴, OA=OB解:也可利用对称性得!DH分析: 1、要求S,应以哪一条线段为底?哪一条线段为高线?3、如何表示出高线?2、如何表示出底边?(别忘了点D的横坐标为t!且DF∥y 轴)(ΔDEH为什么三角形?)解:∵DF ∥y 轴, D的横坐标为t∴F的横坐标也为t∴ HD=HE=1∵ A(q,q)即(-2,-2)∴AC=OC=2∴∠AOC=45o∵DF ∥y 轴 ∴ ∠HDE= ∠AOC=45o又∵DE=易得- 2≤t ≤1,t=0时,S最大=1单位21- 21.二次函数的图象有着丰富的内涵,解决二次函数的题目应尽可能地画出大致的抛物线图象,结合图形,解决问题.利用a、b、c的值可判断二次函数的大致位置情况;反之,若已知二次函数的大致位置,也可以判断出一些特殊关系式或字母的取值范围等.
2.二次函数还与一元二次方程的知识紧密联系.利用方程根的性质、根的判别式,可判定抛物线与x轴交点的情况;反之,可以求某些字母的取值范围. 四、方法小结3.要准确辨析条件,选用适当的形式求二次函数解析式,即已知任意三点坐标选用一般式;已知顶点坐标、对称轴或最值常可选用顶点式;已知抛物线与x轴的两个交点坐标常选用交点式.
