3.3.1 抛物线及其标准方程 同步练习(含解析)
文档属性
| 名称 | 3.3.1 抛物线及其标准方程 同步练习(含解析) | 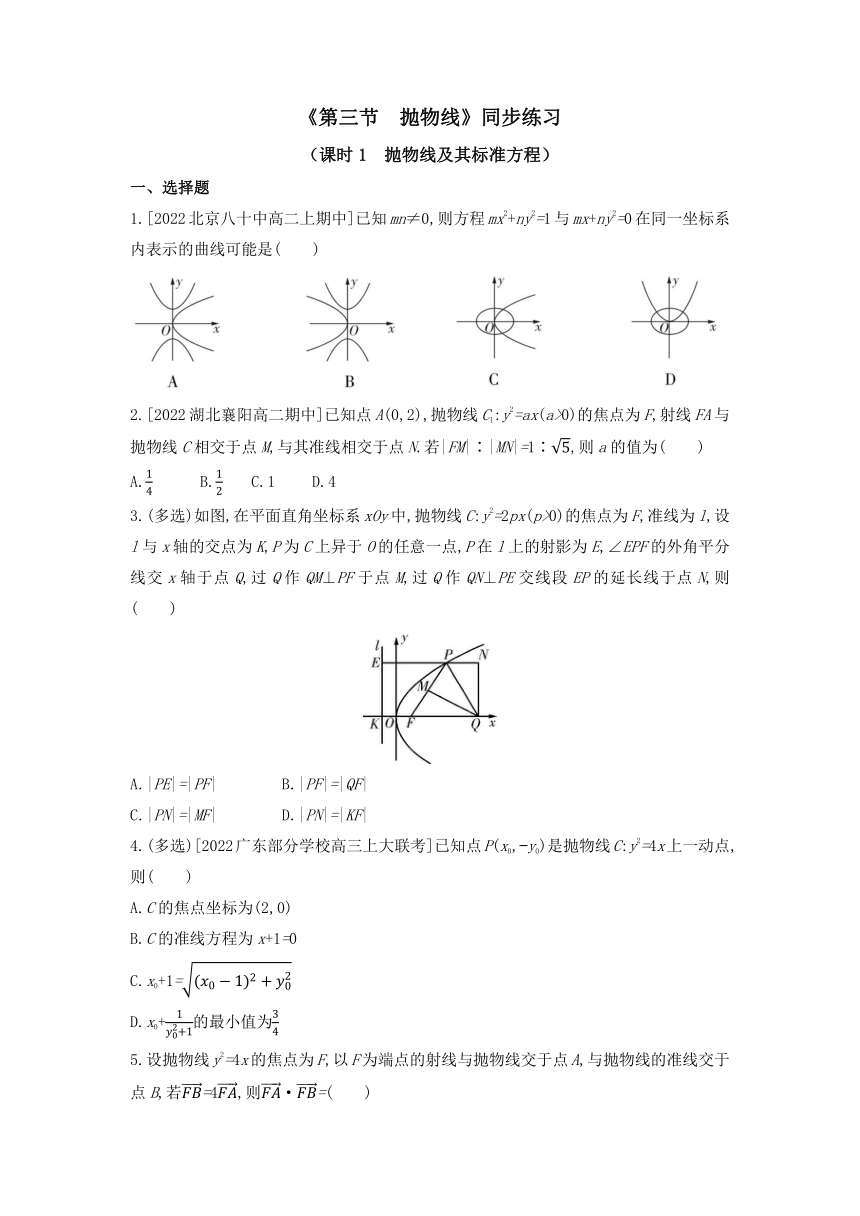 | |
| 格式 | docx | ||
| 文件大小 | 108.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 08:38:55 | ||
图片预览



文档简介
《第三节 抛物线》同步练习
(课时1 抛物线及其标准方程)
一、选择题
1.[2022北京八十中高二上期中]已知mn≠0,则方程mx2+ny2=1与mx+ny2=0在同一坐标系内表示的曲线可能是( )
2.[2022湖北襄阳高二期中]已知点A(0,2),抛物线C1:y2=ax(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N.若|FM|∶|MN|=1∶,则a的值为( )
A. B. C.1 D.4
3.(多选)如图,在平面直角坐标系xOy中,抛物线C:y2=2px(p>0)的焦点为F,准线为l,设l与x轴的交点为K,P为C上异于O的任意一点,P在l上的射影为E,∠EPF的外角平分线交x轴于点Q,过Q作QM⊥PF于点M,过Q作QN⊥PE交线段EP的延长线于点N,则 ( )
A.|PE|=|PF| B.|PF|=|QF|
C.|PN|=|MF| D.|PN|=|KF|
4.(多选)[2022广东部分学校高三上大联考]已知点P(x0, y0)是抛物线C:y2=4x上一动点,则( )
A.C的焦点坐标为(2,0)
B.C的准线方程为x+1=0
C.x0+1=
D.x0+的最小值为
5.设抛物线y2=4x的焦点为F,以F为端点的射线与抛物线交于点A,与抛物线的准线交于点B,若=4,则·=( )
A.9 B.8 C.6 D.4
6.设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则抛物线C的方程为( )
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x
7.[2022天津英华国际学校高二上期中]抛物线y2=2px(p>0)的焦点为F,准线为l,点P为抛物线上一点,PA⊥l,垂足为A.若直线AF的斜率为 ,|PF|=4,则抛物线的方程为( )
A.y2=4x B.y2=4x
C.y2=8x D.y2=8x
二、非选择题
8.[2022湖北孝感高中调考]设F为抛物线y2=4x的焦点,A,B,C为该抛物线上三点,若=0,则||+||+||= .
9.已知抛物线y2=2px(p>0)的焦点为F,点A,B为抛物线上的两个动点,且满足∠AFB=120°,过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则的最大值为 .
10.已知点M(20,40),抛物线y2=2px(p>0)的焦点为F.若对于抛物线上的任意点P,|PM|+|PF|的最小值为41,则p的值为 .
11.在平面直角坐标系xOy中,已知圆F:(x 2)2+y2=1,动圆M与直线l:x= 1相切且与圆F外切.
(1)记圆心M的轨迹为曲线C,求曲线C的方程;
(2)已知A( 2,0),曲线C上一点P满足|PA|=|PF|,求∠PAF的大小.
12.已知以向量v=(1,)为方向向量的直线l过点(0,),抛物线C:y2=2px(p>0)上的点(0,0)关于直线l的对称点在该抛物线的准线上.
(1)求抛物线C的方程;
(2)设A,B是抛物线C上的两个动点,过点A作平行于x轴的直线m,直线OB与直线m交于点N,若·+p2=0(O为坐标原点,A,B异于点O),试求点N的轨迹方程.
参考答案
一、选择题
1.A 由题意,当m=1,n=2时,方程x2+2y2=1表示焦点在x轴上的椭圆,方程x+2y2=0可化为y2=x,表示开口向左的抛物线,故排除C,D;当m= 1时,n=1时,方程y2 x2=1表示焦点在y轴上的双曲线,方程 x+y2=0可化为y2=x,表示开口向右的抛物线,故A符合,B不符合,故选A.
2.D 依题意,点F的坐标为(,0).如图,设点M在准线上的射影为K,由抛物线的定义知|MF|=|KM|,则|KM|∶|MN|=1∶,则|KN|∶|KM|=2∶1.因为kFN==,kFN== 2,所以=2,解得a=4.
3.ABD 由抛物线的定义知A正确;因为∠FQP=∠QPN=∠QPF,所以|PF|=|QF|,B正确;由题意知四边形QKEN为矩形,所以|PN|=|NE| |PE|=|QK| |FQ|=|KF|,D正确;显然当PF⊥x轴时,F,M重合,|PN|≠|MF|,C错误.
4.BCD
5.A 设准线交x轴于点D,点A在准线上的射影为点C,如图.因为=4,所以|FB|=4|FA|,|FA|=|AC|=|DF|,所以·=|FA||FB|=4|FA|2=4×|DF|2=9.
6.C 因为抛物线C的方程为y2=2px(p>0),所以焦点F(,0).设M(x,y),由抛物线的定义,知|MF|=x+=5,得x=5.因为圆心是MF的中点,所以根据中点坐标公式,可得圆心的横坐标为.由已知,得圆的半径也为,所以该圆与y轴相切于点(0,2),故圆心的纵坐标为2,则点M的纵坐标为4,即M(5,4),代入抛物线方程,得p2 10p+16=0,解得p=2或p=8.所以抛物线C的方程为y2=4x或y2=16x.故选C.
7.A 如图,记直线l与x轴的交点为K.因为直线AF的斜率为,所以∠PAF=∠AFK=60°.由抛物线的定义,知|PF|=|PA|=4,所以△PAF为等边三角形,所以|AF|=4,所以在Rt△AKF中,|KF|=2,所以p=2,所以抛物线方程为y2=4x.
二、非选择题
8.6 解析 设A(x1,y1),B(x2,y2),C(x3,y3).又F(1,0),由=0,知(x1 1)+(x2 1)+(x3 1)=0,即x1+x2+x3=3,则||+||+||=x1+x2+x3+p=6.
9. 解析 设|AF|=a,|BF|=b,作AQ垂直抛物线的准线于点Q,BP垂直抛物线的准线于点P.由抛物线的定义,知|AF|=|AQ|,|BF|=|BP|.由余弦定理得|AB|2=a2+b2 2abcos 120°=a2+b2+ab=(a+b)2 ab.又ab≤()2,所以(a+b)2 ab≥(a+b)2(a+b)2=(a+b)2,当且仅当a=b时,等号成立,所以|AB|≥(a+b),所以≤=,即的最大值为.
10.42或22 解析 根据点M与抛物线的位置分类讨论:(1)当点M(20,40)位于抛物线内时,如图1,过点P作抛物线准线的垂线,垂足为D,则|PF|=|PD|,|PM|+|PF|=|PM|+|PD|,当点M,P,D共线时,|PM|+|PF|的值最小.由最小值为41,得20+=41,解得p=42.(2)当点M(20,40)位于抛物线外时,如图2,当点P,M,F共线(P在MF上)时,|PM|+|PF|的值最小.由最小值为41,得=41,解得p=22或58.当p=58时,y2=116x,此时点M(20,40)在抛物线内,故舍去.综上,p=42或22.
11. 解析 (1)设圆心M(x,y),圆M的半径为r.
由题意知,|MF|=r+1,点M到直线l的距离为r.
方法一 点M到点F(2,0)的距离等于点M到定直线x= 2的距离,
根据抛物线的定义,知曲线C是以F(2,0)为焦点,直线x= 2为准线的抛物线.
故曲线C的方程为y2=8x.
方法二 因为|MF| ==r+1,|x+1|=r,x> 1,
所以=x+2,化简得y2=8x, 故曲线C的方程为y2=8x.
(2)方法一 设P(x0,y0),由|PA|=|PF|, 得(x0+2)2+=2[(x0 2)2+],
又=8x0,所以x0=2,故P(2,±4), 所以直线PA的斜率kPA=±1,故∠PAF=.
方法二 过点P向直线x= 2作垂线,垂足为Q.
由抛物线的定义,知|PQ|=|PF|, 所以|PA|=|PQ|,
在△APQ中,因为∠PQA=, 所以sin∠QAP==,
所以∠QAP=,故∠PAF=.
12. 解析 (1)由题意可得直线l:y=x+, ①
过原点且垂直于l的直线方程为y= 2x, ②
由①②,得x=.
因为抛物线上的点(0,0)关于直线l的对称点在该抛物线的准线上,
所以=×2,
所以p=2,所以抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),N(x,y).
由·+p2=0,得x1x2+y1y2+4=0.
又=4x1,=4x2,代入上式,
解得y1y2= 8, ③
又直线ON:y=x,即y=x. ④
由③④及y=y1,得点N的轨迹方程为x= 2(y≠0).
(课时1 抛物线及其标准方程)
一、选择题
1.[2022北京八十中高二上期中]已知mn≠0,则方程mx2+ny2=1与mx+ny2=0在同一坐标系内表示的曲线可能是( )
2.[2022湖北襄阳高二期中]已知点A(0,2),抛物线C1:y2=ax(a>0)的焦点为F,射线FA与抛物线C相交于点M,与其准线相交于点N.若|FM|∶|MN|=1∶,则a的值为( )
A. B. C.1 D.4
3.(多选)如图,在平面直角坐标系xOy中,抛物线C:y2=2px(p>0)的焦点为F,准线为l,设l与x轴的交点为K,P为C上异于O的任意一点,P在l上的射影为E,∠EPF的外角平分线交x轴于点Q,过Q作QM⊥PF于点M,过Q作QN⊥PE交线段EP的延长线于点N,则 ( )
A.|PE|=|PF| B.|PF|=|QF|
C.|PN|=|MF| D.|PN|=|KF|
4.(多选)[2022广东部分学校高三上大联考]已知点P(x0, y0)是抛物线C:y2=4x上一动点,则( )
A.C的焦点坐标为(2,0)
B.C的准线方程为x+1=0
C.x0+1=
D.x0+的最小值为
5.设抛物线y2=4x的焦点为F,以F为端点的射线与抛物线交于点A,与抛物线的准线交于点B,若=4,则·=( )
A.9 B.8 C.6 D.4
6.设抛物线C:y2=2px(p>0)的焦点为F,点M在C上,|MF|=5,若以MF为直径的圆过点(0,2),则抛物线C的方程为( )
A.y2=4x或y2=8x B.y2=2x或y2=8x
C.y2=4x或y2=16x D.y2=2x或y2=16x
7.[2022天津英华国际学校高二上期中]抛物线y2=2px(p>0)的焦点为F,准线为l,点P为抛物线上一点,PA⊥l,垂足为A.若直线AF的斜率为 ,|PF|=4,则抛物线的方程为( )
A.y2=4x B.y2=4x
C.y2=8x D.y2=8x
二、非选择题
8.[2022湖北孝感高中调考]设F为抛物线y2=4x的焦点,A,B,C为该抛物线上三点,若=0,则||+||+||= .
9.已知抛物线y2=2px(p>0)的焦点为F,点A,B为抛物线上的两个动点,且满足∠AFB=120°,过弦AB的中点M作抛物线准线的垂线MN,垂足为N,则的最大值为 .
10.已知点M(20,40),抛物线y2=2px(p>0)的焦点为F.若对于抛物线上的任意点P,|PM|+|PF|的最小值为41,则p的值为 .
11.在平面直角坐标系xOy中,已知圆F:(x 2)2+y2=1,动圆M与直线l:x= 1相切且与圆F外切.
(1)记圆心M的轨迹为曲线C,求曲线C的方程;
(2)已知A( 2,0),曲线C上一点P满足|PA|=|PF|,求∠PAF的大小.
12.已知以向量v=(1,)为方向向量的直线l过点(0,),抛物线C:y2=2px(p>0)上的点(0,0)关于直线l的对称点在该抛物线的准线上.
(1)求抛物线C的方程;
(2)设A,B是抛物线C上的两个动点,过点A作平行于x轴的直线m,直线OB与直线m交于点N,若·+p2=0(O为坐标原点,A,B异于点O),试求点N的轨迹方程.
参考答案
一、选择题
1.A 由题意,当m=1,n=2时,方程x2+2y2=1表示焦点在x轴上的椭圆,方程x+2y2=0可化为y2=x,表示开口向左的抛物线,故排除C,D;当m= 1时,n=1时,方程y2 x2=1表示焦点在y轴上的双曲线,方程 x+y2=0可化为y2=x,表示开口向右的抛物线,故A符合,B不符合,故选A.
2.D 依题意,点F的坐标为(,0).如图,设点M在准线上的射影为K,由抛物线的定义知|MF|=|KM|,则|KM|∶|MN|=1∶,则|KN|∶|KM|=2∶1.因为kFN==,kFN== 2,所以=2,解得a=4.
3.ABD 由抛物线的定义知A正确;因为∠FQP=∠QPN=∠QPF,所以|PF|=|QF|,B正确;由题意知四边形QKEN为矩形,所以|PN|=|NE| |PE|=|QK| |FQ|=|KF|,D正确;显然当PF⊥x轴时,F,M重合,|PN|≠|MF|,C错误.
4.BCD
5.A 设准线交x轴于点D,点A在准线上的射影为点C,如图.因为=4,所以|FB|=4|FA|,|FA|=|AC|=|DF|,所以·=|FA||FB|=4|FA|2=4×|DF|2=9.
6.C 因为抛物线C的方程为y2=2px(p>0),所以焦点F(,0).设M(x,y),由抛物线的定义,知|MF|=x+=5,得x=5.因为圆心是MF的中点,所以根据中点坐标公式,可得圆心的横坐标为.由已知,得圆的半径也为,所以该圆与y轴相切于点(0,2),故圆心的纵坐标为2,则点M的纵坐标为4,即M(5,4),代入抛物线方程,得p2 10p+16=0,解得p=2或p=8.所以抛物线C的方程为y2=4x或y2=16x.故选C.
7.A 如图,记直线l与x轴的交点为K.因为直线AF的斜率为,所以∠PAF=∠AFK=60°.由抛物线的定义,知|PF|=|PA|=4,所以△PAF为等边三角形,所以|AF|=4,所以在Rt△AKF中,|KF|=2,所以p=2,所以抛物线方程为y2=4x.
二、非选择题
8.6 解析 设A(x1,y1),B(x2,y2),C(x3,y3).又F(1,0),由=0,知(x1 1)+(x2 1)+(x3 1)=0,即x1+x2+x3=3,则||+||+||=x1+x2+x3+p=6.
9. 解析 设|AF|=a,|BF|=b,作AQ垂直抛物线的准线于点Q,BP垂直抛物线的准线于点P.由抛物线的定义,知|AF|=|AQ|,|BF|=|BP|.由余弦定理得|AB|2=a2+b2 2abcos 120°=a2+b2+ab=(a+b)2 ab.又ab≤()2,所以(a+b)2 ab≥(a+b)2(a+b)2=(a+b)2,当且仅当a=b时,等号成立,所以|AB|≥(a+b),所以≤=,即的最大值为.
10.42或22 解析 根据点M与抛物线的位置分类讨论:(1)当点M(20,40)位于抛物线内时,如图1,过点P作抛物线准线的垂线,垂足为D,则|PF|=|PD|,|PM|+|PF|=|PM|+|PD|,当点M,P,D共线时,|PM|+|PF|的值最小.由最小值为41,得20+=41,解得p=42.(2)当点M(20,40)位于抛物线外时,如图2,当点P,M,F共线(P在MF上)时,|PM|+|PF|的值最小.由最小值为41,得=41,解得p=22或58.当p=58时,y2=116x,此时点M(20,40)在抛物线内,故舍去.综上,p=42或22.
11. 解析 (1)设圆心M(x,y),圆M的半径为r.
由题意知,|MF|=r+1,点M到直线l的距离为r.
方法一 点M到点F(2,0)的距离等于点M到定直线x= 2的距离,
根据抛物线的定义,知曲线C是以F(2,0)为焦点,直线x= 2为准线的抛物线.
故曲线C的方程为y2=8x.
方法二 因为|MF| ==r+1,|x+1|=r,x> 1,
所以=x+2,化简得y2=8x, 故曲线C的方程为y2=8x.
(2)方法一 设P(x0,y0),由|PA|=|PF|, 得(x0+2)2+=2[(x0 2)2+],
又=8x0,所以x0=2,故P(2,±4), 所以直线PA的斜率kPA=±1,故∠PAF=.
方法二 过点P向直线x= 2作垂线,垂足为Q.
由抛物线的定义,知|PQ|=|PF|, 所以|PA|=|PQ|,
在△APQ中,因为∠PQA=, 所以sin∠QAP==,
所以∠QAP=,故∠PAF=.
12. 解析 (1)由题意可得直线l:y=x+, ①
过原点且垂直于l的直线方程为y= 2x, ②
由①②,得x=.
因为抛物线上的点(0,0)关于直线l的对称点在该抛物线的准线上,
所以=×2,
所以p=2,所以抛物线C的方程为y2=4x.
(2)设A(x1,y1),B(x2,y2),N(x,y).
由·+p2=0,得x1x2+y1y2+4=0.
又=4x1,=4x2,代入上式,
解得y1y2= 8, ③
又直线ON:y=x,即y=x. ④
由③④及y=y1,得点N的轨迹方程为x= 2(y≠0).
