8.5.3 平面与平面平行 同步练习(含解析)
文档属性
| 名称 | 8.5.3 平面与平面平行 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 417.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 08:43:37 | ||
图片预览




文档简介
《第五节 空间直线、平面的平行》同步练习
(课时3 平面与平面平行)
一、基础巩固
知识点1 平面与平面平行的判定
1.[2022广东中山高一期末]在下列条件中,可判定平面α与平面β平行的是( )
A.α,β都平行于直线a
B.α内存在不共线的三点到β的距离相等
C.l,m是α内的两条直线,且l∥β,m∥β
D.l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β
2.[2022安徽皖南名校高一下期中联考]已知m α,n α,l1 β,l2 β,l1∩l2=M,则α∥β的一个充分条件是( )
A.m∥β且l1∥α B.m∥β且n∥β
C.m∥β且n∥l2 D.m∥l1且n∥l2
3.如图,在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1D1,A1B1的中点,过直线BD的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )
A. B. C. D.
4.[2022江苏省太湖高级中学高一期中]如图,在三棱柱ABC-A1B1C1中,M,N,P分别为AB,BC,B1C1的中点.
(1)求证:AC∥平面B1MN;
(2)求证:平面ACP∥平面B1MN.
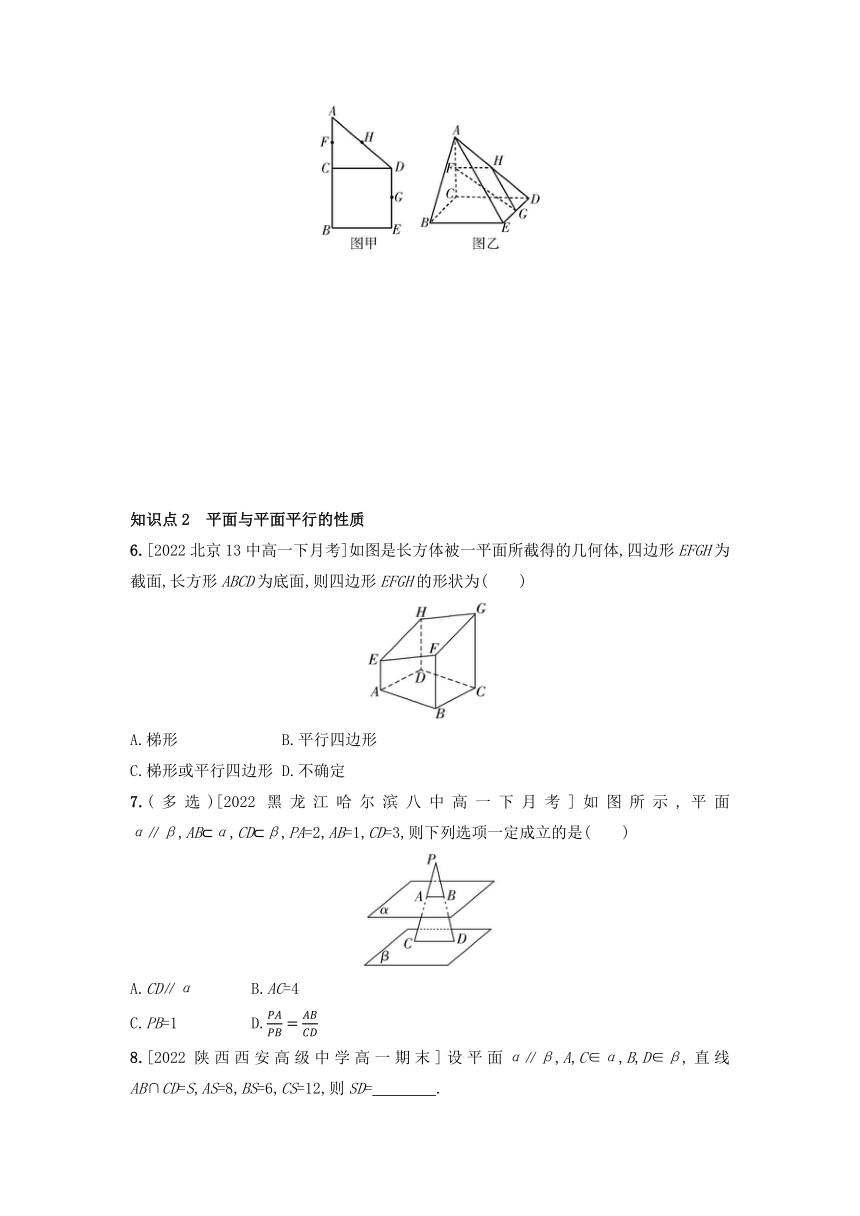
5.如图甲,在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,F,H,G分别为AC,AD,DE的中点,现将△ACD沿CD折起,如图乙.求证:平面FHG∥平面ABE.
知识点2 平面与平面平行的性质
6.[2022北京13中高一下月考]如图是长方体被一平面所截得的几何体,四边形EFGH为截面,长方形ABCD为底面,则四边形EFGH的形状为( )
A.梯形 B.平行四边形
C.梯形或平行四边形 D.不确定
7.(多选)[2022黑龙江哈尔滨八中高一下月考]如图所示,平面α∥β,AB α,CD β,PA=2,AB=1,CD=3,则下列选项一定成立的是( )
A.CD∥α B.AC=4
C.PB=1 D.
8.[2022陕西西安高级中学高一期末]设平面α∥β,A,C∈α,B,D∈β,直线AB∩CD=S,AS=8,BS=6,CS=12,则SD= .
9.如图所示,正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱A1B1,B1C1的中点,P是棱AD上的一点,AP=1,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ= .
10.如图,在三棱柱ABC-A1B1C1中,E,F,G分别为B1C1,A1B1,AB的中点.
(1)求证:平面A1C1G∥平面BEF;
(2)若平面A1C1G∩BC=H,求证:H为BC的中点.
11.[2022福建三明高一期中]如图,已知在多面体EABCDF中,四边形ABCD是正方形,EA⊥平面ABCD,FD∥EA,且FD=EA.
(1)求证:FC∥平面ABE;
(2)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面ECF平行,要求保留作图痕迹,但不要求证明.
二、能力提升
1.在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q为CC1上的点,要使平面D1BQ∥平面PAO,则点Q( )
A.与C重合
B.与C1重合
C.为CC1的三等分点
D.为CC1的中点
2.[2022山西省太原市第五中学校高一下阶段性检测]如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE∥平面SBD,则动点P的轨迹与△SCD组成的相关图形最有可能是图中的( )
3.(多选)如图,在棱长均相等的四棱锥P-ABCD中,O为底面正方形的中心,M,N分别为侧棱PA,PB的中点,则下列结论正确的有( )
A.OM∥PC
B.PD∥平面OMN
C.平面PCD∥平面OMN
D.ON∥PA
4.(多选)如图,平面α∥平面β,A,C是平面α内不同的两点,B,D是平面β内不同的两点,E,F分别是线段AB,CD的中点,则下列说法正确的是( )
A.当AB,CD共面时,AC∥BD
B.当AB∥CD时,AC=BD
C.当AB=2CD时,E,F两点不可能重合
D.当AB,CD是异面直线时,EF∥α
5.[2022江苏省无锡市天一中学高一下期中]直三棱柱ABC-A1B1C1的所有棱长均为3,D为侧棱CC1的中点,M为侧棱AA1上一点,且A1M=1,N为B1C1上一点,且MN∥平面ABD,则NB1的长为( )
A.1 B.2 C. D.
6.[2022广西贺州昭平中学高一期末]如图,在圆柱O1O2中,AB,CD分别是上、下底面圆的直径,且AB∥CD,EF,GH是圆柱的一个轴截面上的母线.
(1)若CE=DE=2,圆柱的母线长等于底面圆的直径,求圆柱的表面积.
(2)证明:平面ABH∥平面ECD.
7.如图所示,矩形ABCD和矩形ABEF中,AF=AD,点M,N分别位于AE,DB上(点M异于点A,点N异于点D),且AM=DN,矩形ABEF可沿AB任意翻折.
(1)求证:当F,A,D不共线时,MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,MN总和FD平行.”这个结论对吗 如果对,请证明;如果不对,请说明能否改变个别已知条件使上述结论成立.
8.如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上.
(1)若PM∶MA=BN∶ND=PQ∶QD,求证:平面MNQ∥平面PBC;
(2)若点Q满足PQ∶QD=2∶1,则点M满足什么条件时,BM∥平面AQC
参考答案
一、基础巩固
1.D
A 当α∩β=l,l∥a,a α且a β时,满足α,β都平行于直线a,不能推出α∥β.
B 当α∩β=b,且在α内直线b一侧有两点,另一侧有一点,三点到β的距离相等时,不能推出α∥β.
C 当l与m平行时,不能推出α∥β.
D √ 因为l∥α,m∥α,所以在α内有两条直线l',m',使得l'∥l,m'∥m.因为l与m异面,则l'与m'相交.又l∥β,m∥β,则l'∥β,m'∥β,所以α∥β.
2.D 对于A,若m∥β且l1∥α,则α,β可能相交,故A错误;对于B,若m∥β且n∥β,要得出α∥β,必须满足m,n相交,故B错误;对于C,若m∥β且n∥l2,要得出α∥β,必须满足m,n相交,故C错误;对于D,由平面与平面平行的判定定理,可知α∥β,故D正确.
3.B 如图,取C1D1,B1C1的中点分别为P,Q,连接B1D1,NP.易知MN∥B1D1∥BD, AD NP,所以四边形ANPD为平行四边形,所以AN∥DP.又BD和DP为平面DBQP内的两条相交直线,所以平面DBQP∥平面AMN,则四边形DBQP的面积即为所求.因为PQ∥DB,PQ=BD=,所以四边形DBQP为梯形,其高为h=,所以梯形DBQP的面积为(PQ+BD)h=×()×.故选B.
4.证明(1)由于M,N分别为AB,BC的中点,故MN∥AC,所以MN是△ABC的中位线,
而AC 平面B1MN,MN 平面B1MN,
故AC∥平面B1MN.
(2)在三棱柱ABC-A1B1C1中,由于N,P分别为BC,B1C1的中点,故B1P∥CN,B1P=CN,
故四边形B1PCN为平行四边形,故PC∥B1N,
而PC 平面B1MN,B1N 平面B1MN,故PC∥平面B1MN,
由(1)知,AC∥平面B1MN,且AC∩PC=C,AC,PC 平面ACP,故平面ACP∥平面B1MN.
5.证明因为F,H,G分别为AC,AD,DE的中点,所以FH∥CD,HG∥AE.
在题图甲中,AB⊥CD,AB⊥BE,所以CD∥BE,所以FH∥BE.
因为BE 平面ABE,FH 平面ABE,所以FH∥平面ABE.
因为AE 平面ABE,HG 平面ABE,所以HG∥平面ABE.
又FH∩HG=H,所以平面FHG∥平面ABE.
6.B 因为平面ABFE∥平面DCGH,平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,所以EF∥HG.同理,EH∥FG,所以四边形EFGH是平行四边形.
7.AB 对于A,因为α∥β,CD β,所以CD∥α,故A正确;对于B,设由PC与PD所确定的平面为γ,因为α∥β,α∩γ=AB,β∩γ=CD,所以AB∥CD,所以,即,解得AC=4,故B正确;对于C,若PB=1,则PB+AB=PA,这与三角形的三边关系相矛盾,故C错误;对于D,若,则由,知PB=PC,但PB与PC的长度关系不确定,故D错误.
8.9 解析根据题意可作图如下:
因为直线AB∩CD=S,故可设它们确定的平面为γ,如图1,图2,则γ和α的交线为AC,和β的交线为BD,因为α∥β,故AC∥BD,故,即,解得SD=9.
9.2 解析因为平面ABCD∥平面A1B1C1D1,平面ABCD∩平面PQNM=PQ,平面A1B1C1D1∩平面PQNM=MN,所以MN∥PQ.连接A1C1,AC,则MN∥A1C1,A1C1∥AC,所以PQ∥AC.又AP=1,所以,所以PQ=AC=×3=2.
10.证明(1)因为E,F分别为B1C1,A1B1的中点,所以EF∥A1C1.
因为A1C1 平面A1C1G,EF 平面A1C1G,
所以EF∥平面A1C1G.
又F,G分别为A1B1,AB的中点,所以A1F=BG,A1F∥BG,
所以四边形A1GBF为平行四边形,所以BF∥A1G.
因为A1G 平面A1C1G,BF 平面A1C1G,所以BF∥平面A1C1G.
又EF∩BF=F,所以平面A1C1G∥平面BEF.
(2)连接GH,因为平面A1C1G与平面ABC有公共点G,且平面A1C1G∩BC=H,所以平面A1C1G∩平面ABC=GH.
又平面ABC∥平面A1B1C1,平面A1C1G∩平面A1B1C1=A1C1,所以A1C1∥GH,所以GH∥AC.
因为G为AB的中点,所以H为BC的中点.
11.解析(1)因为FD∥EA,FD 平面ABE,EA 平面ABE,所以FD∥平面ABE.
在正方形ABCD中,AB∥CD,又AB 平面ABE,CD 平面ABE,所以CD∥平面ABE.
由于FD∩CD=D,所以平面ABE∥平面DCF,
又FC 平面DCF,所以FC∥平面ABE.
(2)设G,H,P分别是BE,AE,CD的中点,作图如图所示,
则KP∥平面ECF.
二、能力提升
1.D 当Q为CC1的中点时,平面D1BQ∥平面PAO.证明如下:因为Q为CC1的中点,P是DD1的中点,所以QB∥PA,又QB 平面PAO,所以QB∥平面PAO.连接DB,因为P,O分别为DD1,DB的中点,所以D1B∥PO.因为D1B 平面PAO,所以D1B∥平面PAO.又D1B∩QB=B,所以平面D1BQ∥平面PAO.
2.A 如图,分别取CD,SC的中点M,N,连接MN,ME,NE,因为E是BC的中点,所以EM∥BD,EN∥SB,又EM,EN 平面SBD,BD,SB 平面SBD,所以EM∥平面SBD,EN∥平面SBD.因为EM∩EN=E,EM,EN 平面EMN,所以平面EMN∥平面SBD,所以当P在MN上移动时,PE 平面EMN,此时能够保持PE∥平面SBD,则动点P的轨迹与△SCD组成的相关图形是选项A.故选A.
3.ABC 对于A,连接AC,则O为AC的中点.又M为PA的中点,所以OM∥PC,A正确;对于B,连接BD,显然O为BD的中点,又N为PB的中点,所以PD∥ON,由线面平行的判定定理,可得PD∥平面OMN,B正确;对于C,因为OM∥PC,所以由线面平行的判定定理,可得PC∥平面OMN,又由选项B得PD∥平面OMN,由面面平行的判定定理,可得平面PCD∥平面OMN,C正确;对于D,由B的分析知ON∥PD,则ON∥平面PAD,在平面PAD中,PA与PD相交,则PA与ON不平行,D错误.故选ABC.
4.ABD 对于A,当AB,CD共面时,平面ABDC∩平面α=AC,平面ABDC∩平面β=BD,因为α∥β,所以AC∥BD,故A正确;对于B,当AB∥CD时,A,B,C,D四点共面,易得AC∥BD,故四边形ABDC为平行四边形,所以AC=BD,故B正确;对于C,如图1所示,当AB,CD相交且AE=2CE时,满足AB=2CD,此时E,F两点重合,故C错误;对于D,如图2所示,连接AD,取AD的中点M,连接EF,EM,FM,因为E,F分别是线段AB,CD的中点,所以EM∥BD,FM∥AC,又FM α,AC α,EM β,BD β,所以FM∥α,EM∥β,又α∥β,所以EM∥α,因为EM∩FM=M,所以平面EFM∥α,所以EF∥α,故D正确.
5.B 如图所示,过点M作MP∥AB交BB1于点P,再过点P作PN∥BD交B1C1于点N,取BB1中点为Q,连接C1Q.因为MP∥AB,MP 平面ABD,AB 平面ABD,所以MP∥平面ABD,同理,PN∥平面ABD,又MP∩PN=P,MP,PN 平面MPN,所以平面MPN∥平面ABD.又MN 平面MPN,所以MN∥平面ABD,又由题意知,四边形ABB1A1与四边形BCC1B1都是边长为3的正方形.因为A1M=1,MP∥AB,所以B1P=1,因为Q是BB1中点,所以B1Q=BB1=,又D为侧棱CC1的中点,所以BQ C1D,所以四边形BQC1D是平行四边形,所以C1Q∥BD,所以C1Q∥PN,所以△B1PN∽△B1QC1,所以,即,解得NB1=2.故选B.
6.解析(1)如图,连接CF,DF.
因为DE=CE,EF⊥CF,EF⊥DF,
所以△CEF≌△DEF,所以CF=DF.
因为CD为直径,记底面半径为R,则EF=2R,
则CF2+DF2=4R2,所以DF=R.
又DF2+EF2=DE2,所以(R)2+(2R)2=(2)2,解得R=2.
所以圆柱的表面积S=2πR×2R+2πR2=24π.
(2)如图,连接O1E,O2H,O1H,O2E.
由圆柱性质知O1E∥O2H且O1E=O2H,
所以四边形HO2EO1为平行四边形,所以O1H∥O2E.
又O1H 平面CDE,O2E 平面CDE,所以O1H∥平面CDE.
因为AB∥CD,AB 平面CDE,CD 平面CDE,所以AB∥平面CDE,
又AB∩O1H=O1,O1H 平面ABH,AB 平面ABH,
所以平面ABH∥平面ECD.
7.解析(1)在平面图形中,连接MN,设MN与AB交于点G.
因为四边形ABCD和四边形ABEF都是矩形,且AD=AF,
所以AD∥BE且AD=BE,
所以四边形ADBE是平行四边形,所以AE=BD.
又AM=DN,所以MN∥AD.翻折之后,如图所示.
因为MG∥AF,NG∥AD,MG∩NG=G,
所以平面GNM∥平面ADF.
又MN 平面GNM,所以MN∥平面ADF.
所以当F,A,D不共线时,MN总平行于平面ADF.
(2)这个结论不对.
要使上述结论成立,M,N应分别为AE,BD的中点.
翻折后连接FB.
在△BDF中,因为M,N分别为BF,BD的中点,
所以MN∥FD.
8.解析(1)因为PM∶MA=PQ∶QD,
所以MQ∥AD.
因为底面ABCD是平行四边形,
所以AD∥BC,所以MQ∥BC.
因为MQ 平面PBC,BC 平面PBC,所以MQ∥平面PBC.
因为BN∶ND=PQ∶QD,所以QN∥PB.
因为QN 平面PBC,PB 平面PBC,所以QN∥平面PBC.
因为MQ∩QN=Q,MQ,QN 平面MNQ,
所以平面MNQ∥平面PBC.
(2)当点M为PA的中点时,BM∥平面AQC.
证明如下:设BD交AC于点O,则点O为BD的中点,取PQ的中点E,连接ME,BE.
因为PQ∶QD=2∶1,且E为PQ的中点,
所以PE=EQ=QD,所以Q为DE的中点.
又点O为BD的中点,所以BE∥OQ.
因为BE 平面AQC,OQ 平面AQC,所以BE∥平面AQC.
因为点M,E分别为PA,PQ的中点,所以ME∥AQ.
因为ME 平面AQC,AQ 平面AQC,所以ME∥平面AQC.
因为BE∩ME=E,BE,ME 平面BME,
所以平面BME∥平面AQC.
因为BM 平面BME,所以BM∥平面AQC.
所以当点M是PA的中点时,BM∥平面AQC.
(课时3 平面与平面平行)
一、基础巩固
知识点1 平面与平面平行的判定
1.[2022广东中山高一期末]在下列条件中,可判定平面α与平面β平行的是( )
A.α,β都平行于直线a
B.α内存在不共线的三点到β的距离相等
C.l,m是α内的两条直线,且l∥β,m∥β
D.l,m是两条异面直线,且l∥α,m∥α,l∥β,m∥β
2.[2022安徽皖南名校高一下期中联考]已知m α,n α,l1 β,l2 β,l1∩l2=M,则α∥β的一个充分条件是( )
A.m∥β且l1∥α B.m∥β且n∥β
C.m∥β且n∥l2 D.m∥l1且n∥l2
3.如图,在棱长为1的正方体ABCD-A1B1C1D1中,M,N分别是A1D1,A1B1的中点,过直线BD的平面α∥平面AMN,则平面α截该正方体所得截面的面积为( )
A. B. C. D.
4.[2022江苏省太湖高级中学高一期中]如图,在三棱柱ABC-A1B1C1中,M,N,P分别为AB,BC,B1C1的中点.
(1)求证:AC∥平面B1MN;
(2)求证:平面ACP∥平面B1MN.
5.如图甲,在直角梯形ABED中,AB∥DE,AB⊥BE,AB⊥CD,F,H,G分别为AC,AD,DE的中点,现将△ACD沿CD折起,如图乙.求证:平面FHG∥平面ABE.
知识点2 平面与平面平行的性质
6.[2022北京13中高一下月考]如图是长方体被一平面所截得的几何体,四边形EFGH为截面,长方形ABCD为底面,则四边形EFGH的形状为( )
A.梯形 B.平行四边形
C.梯形或平行四边形 D.不确定
7.(多选)[2022黑龙江哈尔滨八中高一下月考]如图所示,平面α∥β,AB α,CD β,PA=2,AB=1,CD=3,则下列选项一定成立的是( )
A.CD∥α B.AC=4
C.PB=1 D.
8.[2022陕西西安高级中学高一期末]设平面α∥β,A,C∈α,B,D∈β,直线AB∩CD=S,AS=8,BS=6,CS=12,则SD= .
9.如图所示,正方体ABCD-A1B1C1D1的棱长为3,M,N分别是棱A1B1,B1C1的中点,P是棱AD上的一点,AP=1,过P,M,N的平面交上底面于PQ,Q在CD上,则PQ= .
10.如图,在三棱柱ABC-A1B1C1中,E,F,G分别为B1C1,A1B1,AB的中点.
(1)求证:平面A1C1G∥平面BEF;
(2)若平面A1C1G∩BC=H,求证:H为BC的中点.
11.[2022福建三明高一期中]如图,已知在多面体EABCDF中,四边形ABCD是正方形,EA⊥平面ABCD,FD∥EA,且FD=EA.
(1)求证:FC∥平面ABE;
(2)记线段BC的中点为K,在平面ABCD内过点K作一条直线与平面ECF平行,要求保留作图痕迹,但不要求证明.
二、能力提升
1.在正方体ABCD-A1B1C1D1中,O为底面ABCD的中心,P是DD1的中点,设Q为CC1上的点,要使平面D1BQ∥平面PAO,则点Q( )
A.与C重合
B.与C1重合
C.为CC1的三等分点
D.为CC1的中点
2.[2022山西省太原市第五中学校高一下阶段性检测]如图,在正四棱锥S-ABCD中,E是BC的中点,P点在侧面△SCD内及其边界上运动,并且总是保持PE∥平面SBD,则动点P的轨迹与△SCD组成的相关图形最有可能是图中的( )
3.(多选)如图,在棱长均相等的四棱锥P-ABCD中,O为底面正方形的中心,M,N分别为侧棱PA,PB的中点,则下列结论正确的有( )
A.OM∥PC
B.PD∥平面OMN
C.平面PCD∥平面OMN
D.ON∥PA
4.(多选)如图,平面α∥平面β,A,C是平面α内不同的两点,B,D是平面β内不同的两点,E,F分别是线段AB,CD的中点,则下列说法正确的是( )
A.当AB,CD共面时,AC∥BD
B.当AB∥CD时,AC=BD
C.当AB=2CD时,E,F两点不可能重合
D.当AB,CD是异面直线时,EF∥α
5.[2022江苏省无锡市天一中学高一下期中]直三棱柱ABC-A1B1C1的所有棱长均为3,D为侧棱CC1的中点,M为侧棱AA1上一点,且A1M=1,N为B1C1上一点,且MN∥平面ABD,则NB1的长为( )
A.1 B.2 C. D.
6.[2022广西贺州昭平中学高一期末]如图,在圆柱O1O2中,AB,CD分别是上、下底面圆的直径,且AB∥CD,EF,GH是圆柱的一个轴截面上的母线.
(1)若CE=DE=2,圆柱的母线长等于底面圆的直径,求圆柱的表面积.
(2)证明:平面ABH∥平面ECD.
7.如图所示,矩形ABCD和矩形ABEF中,AF=AD,点M,N分别位于AE,DB上(点M异于点A,点N异于点D),且AM=DN,矩形ABEF可沿AB任意翻折.
(1)求证:当F,A,D不共线时,MN总平行于平面ADF.
(2)“不管怎样翻折矩形ABEF,MN总和FD平行.”这个结论对吗 如果对,请证明;如果不对,请说明能否改变个别已知条件使上述结论成立.
8.如图,已知四棱锥P-ABCD中,底面ABCD为平行四边形,点M,N,Q分别在PA,BD,PD上.
(1)若PM∶MA=BN∶ND=PQ∶QD,求证:平面MNQ∥平面PBC;
(2)若点Q满足PQ∶QD=2∶1,则点M满足什么条件时,BM∥平面AQC
参考答案
一、基础巩固
1.D
A 当α∩β=l,l∥a,a α且a β时,满足α,β都平行于直线a,不能推出α∥β.
B 当α∩β=b,且在α内直线b一侧有两点,另一侧有一点,三点到β的距离相等时,不能推出α∥β.
C 当l与m平行时,不能推出α∥β.
D √ 因为l∥α,m∥α,所以在α内有两条直线l',m',使得l'∥l,m'∥m.因为l与m异面,则l'与m'相交.又l∥β,m∥β,则l'∥β,m'∥β,所以α∥β.
2.D 对于A,若m∥β且l1∥α,则α,β可能相交,故A错误;对于B,若m∥β且n∥β,要得出α∥β,必须满足m,n相交,故B错误;对于C,若m∥β且n∥l2,要得出α∥β,必须满足m,n相交,故C错误;对于D,由平面与平面平行的判定定理,可知α∥β,故D正确.
3.B 如图,取C1D1,B1C1的中点分别为P,Q,连接B1D1,NP.易知MN∥B1D1∥BD, AD NP,所以四边形ANPD为平行四边形,所以AN∥DP.又BD和DP为平面DBQP内的两条相交直线,所以平面DBQP∥平面AMN,则四边形DBQP的面积即为所求.因为PQ∥DB,PQ=BD=,所以四边形DBQP为梯形,其高为h=,所以梯形DBQP的面积为(PQ+BD)h=×()×.故选B.
4.证明(1)由于M,N分别为AB,BC的中点,故MN∥AC,所以MN是△ABC的中位线,
而AC 平面B1MN,MN 平面B1MN,
故AC∥平面B1MN.
(2)在三棱柱ABC-A1B1C1中,由于N,P分别为BC,B1C1的中点,故B1P∥CN,B1P=CN,
故四边形B1PCN为平行四边形,故PC∥B1N,
而PC 平面B1MN,B1N 平面B1MN,故PC∥平面B1MN,
由(1)知,AC∥平面B1MN,且AC∩PC=C,AC,PC 平面ACP,故平面ACP∥平面B1MN.
5.证明因为F,H,G分别为AC,AD,DE的中点,所以FH∥CD,HG∥AE.
在题图甲中,AB⊥CD,AB⊥BE,所以CD∥BE,所以FH∥BE.
因为BE 平面ABE,FH 平面ABE,所以FH∥平面ABE.
因为AE 平面ABE,HG 平面ABE,所以HG∥平面ABE.
又FH∩HG=H,所以平面FHG∥平面ABE.
6.B 因为平面ABFE∥平面DCGH,平面EFGH∩平面ABFE=EF,平面EFGH∩平面DCGH=HG,所以EF∥HG.同理,EH∥FG,所以四边形EFGH是平行四边形.
7.AB 对于A,因为α∥β,CD β,所以CD∥α,故A正确;对于B,设由PC与PD所确定的平面为γ,因为α∥β,α∩γ=AB,β∩γ=CD,所以AB∥CD,所以,即,解得AC=4,故B正确;对于C,若PB=1,则PB+AB=PA,这与三角形的三边关系相矛盾,故C错误;对于D,若,则由,知PB=PC,但PB与PC的长度关系不确定,故D错误.
8.9 解析根据题意可作图如下:
因为直线AB∩CD=S,故可设它们确定的平面为γ,如图1,图2,则γ和α的交线为AC,和β的交线为BD,因为α∥β,故AC∥BD,故,即,解得SD=9.
9.2 解析因为平面ABCD∥平面A1B1C1D1,平面ABCD∩平面PQNM=PQ,平面A1B1C1D1∩平面PQNM=MN,所以MN∥PQ.连接A1C1,AC,则MN∥A1C1,A1C1∥AC,所以PQ∥AC.又AP=1,所以,所以PQ=AC=×3=2.
10.证明(1)因为E,F分别为B1C1,A1B1的中点,所以EF∥A1C1.
因为A1C1 平面A1C1G,EF 平面A1C1G,
所以EF∥平面A1C1G.
又F,G分别为A1B1,AB的中点,所以A1F=BG,A1F∥BG,
所以四边形A1GBF为平行四边形,所以BF∥A1G.
因为A1G 平面A1C1G,BF 平面A1C1G,所以BF∥平面A1C1G.
又EF∩BF=F,所以平面A1C1G∥平面BEF.
(2)连接GH,因为平面A1C1G与平面ABC有公共点G,且平面A1C1G∩BC=H,所以平面A1C1G∩平面ABC=GH.
又平面ABC∥平面A1B1C1,平面A1C1G∩平面A1B1C1=A1C1,所以A1C1∥GH,所以GH∥AC.
因为G为AB的中点,所以H为BC的中点.
11.解析(1)因为FD∥EA,FD 平面ABE,EA 平面ABE,所以FD∥平面ABE.
在正方形ABCD中,AB∥CD,又AB 平面ABE,CD 平面ABE,所以CD∥平面ABE.
由于FD∩CD=D,所以平面ABE∥平面DCF,
又FC 平面DCF,所以FC∥平面ABE.
(2)设G,H,P分别是BE,AE,CD的中点,作图如图所示,
则KP∥平面ECF.
二、能力提升
1.D 当Q为CC1的中点时,平面D1BQ∥平面PAO.证明如下:因为Q为CC1的中点,P是DD1的中点,所以QB∥PA,又QB 平面PAO,所以QB∥平面PAO.连接DB,因为P,O分别为DD1,DB的中点,所以D1B∥PO.因为D1B 平面PAO,所以D1B∥平面PAO.又D1B∩QB=B,所以平面D1BQ∥平面PAO.
2.A 如图,分别取CD,SC的中点M,N,连接MN,ME,NE,因为E是BC的中点,所以EM∥BD,EN∥SB,又EM,EN 平面SBD,BD,SB 平面SBD,所以EM∥平面SBD,EN∥平面SBD.因为EM∩EN=E,EM,EN 平面EMN,所以平面EMN∥平面SBD,所以当P在MN上移动时,PE 平面EMN,此时能够保持PE∥平面SBD,则动点P的轨迹与△SCD组成的相关图形是选项A.故选A.
3.ABC 对于A,连接AC,则O为AC的中点.又M为PA的中点,所以OM∥PC,A正确;对于B,连接BD,显然O为BD的中点,又N为PB的中点,所以PD∥ON,由线面平行的判定定理,可得PD∥平面OMN,B正确;对于C,因为OM∥PC,所以由线面平行的判定定理,可得PC∥平面OMN,又由选项B得PD∥平面OMN,由面面平行的判定定理,可得平面PCD∥平面OMN,C正确;对于D,由B的分析知ON∥PD,则ON∥平面PAD,在平面PAD中,PA与PD相交,则PA与ON不平行,D错误.故选ABC.
4.ABD 对于A,当AB,CD共面时,平面ABDC∩平面α=AC,平面ABDC∩平面β=BD,因为α∥β,所以AC∥BD,故A正确;对于B,当AB∥CD时,A,B,C,D四点共面,易得AC∥BD,故四边形ABDC为平行四边形,所以AC=BD,故B正确;对于C,如图1所示,当AB,CD相交且AE=2CE时,满足AB=2CD,此时E,F两点重合,故C错误;对于D,如图2所示,连接AD,取AD的中点M,连接EF,EM,FM,因为E,F分别是线段AB,CD的中点,所以EM∥BD,FM∥AC,又FM α,AC α,EM β,BD β,所以FM∥α,EM∥β,又α∥β,所以EM∥α,因为EM∩FM=M,所以平面EFM∥α,所以EF∥α,故D正确.
5.B 如图所示,过点M作MP∥AB交BB1于点P,再过点P作PN∥BD交B1C1于点N,取BB1中点为Q,连接C1Q.因为MP∥AB,MP 平面ABD,AB 平面ABD,所以MP∥平面ABD,同理,PN∥平面ABD,又MP∩PN=P,MP,PN 平面MPN,所以平面MPN∥平面ABD.又MN 平面MPN,所以MN∥平面ABD,又由题意知,四边形ABB1A1与四边形BCC1B1都是边长为3的正方形.因为A1M=1,MP∥AB,所以B1P=1,因为Q是BB1中点,所以B1Q=BB1=,又D为侧棱CC1的中点,所以BQ C1D,所以四边形BQC1D是平行四边形,所以C1Q∥BD,所以C1Q∥PN,所以△B1PN∽△B1QC1,所以,即,解得NB1=2.故选B.
6.解析(1)如图,连接CF,DF.
因为DE=CE,EF⊥CF,EF⊥DF,
所以△CEF≌△DEF,所以CF=DF.
因为CD为直径,记底面半径为R,则EF=2R,
则CF2+DF2=4R2,所以DF=R.
又DF2+EF2=DE2,所以(R)2+(2R)2=(2)2,解得R=2.
所以圆柱的表面积S=2πR×2R+2πR2=24π.
(2)如图,连接O1E,O2H,O1H,O2E.
由圆柱性质知O1E∥O2H且O1E=O2H,
所以四边形HO2EO1为平行四边形,所以O1H∥O2E.
又O1H 平面CDE,O2E 平面CDE,所以O1H∥平面CDE.
因为AB∥CD,AB 平面CDE,CD 平面CDE,所以AB∥平面CDE,
又AB∩O1H=O1,O1H 平面ABH,AB 平面ABH,
所以平面ABH∥平面ECD.
7.解析(1)在平面图形中,连接MN,设MN与AB交于点G.
因为四边形ABCD和四边形ABEF都是矩形,且AD=AF,
所以AD∥BE且AD=BE,
所以四边形ADBE是平行四边形,所以AE=BD.
又AM=DN,所以MN∥AD.翻折之后,如图所示.
因为MG∥AF,NG∥AD,MG∩NG=G,
所以平面GNM∥平面ADF.
又MN 平面GNM,所以MN∥平面ADF.
所以当F,A,D不共线时,MN总平行于平面ADF.
(2)这个结论不对.
要使上述结论成立,M,N应分别为AE,BD的中点.
翻折后连接FB.
在△BDF中,因为M,N分别为BF,BD的中点,
所以MN∥FD.
8.解析(1)因为PM∶MA=PQ∶QD,
所以MQ∥AD.
因为底面ABCD是平行四边形,
所以AD∥BC,所以MQ∥BC.
因为MQ 平面PBC,BC 平面PBC,所以MQ∥平面PBC.
因为BN∶ND=PQ∶QD,所以QN∥PB.
因为QN 平面PBC,PB 平面PBC,所以QN∥平面PBC.
因为MQ∩QN=Q,MQ,QN 平面MNQ,
所以平面MNQ∥平面PBC.
(2)当点M为PA的中点时,BM∥平面AQC.
证明如下:设BD交AC于点O,则点O为BD的中点,取PQ的中点E,连接ME,BE.
因为PQ∶QD=2∶1,且E为PQ的中点,
所以PE=EQ=QD,所以Q为DE的中点.
又点O为BD的中点,所以BE∥OQ.
因为BE 平面AQC,OQ 平面AQC,所以BE∥平面AQC.
因为点M,E分别为PA,PQ的中点,所以ME∥AQ.
因为ME 平面AQC,AQ 平面AQC,所以ME∥平面AQC.
因为BE∩ME=E,BE,ME 平面BME,
所以平面BME∥平面AQC.
因为BM 平面BME,所以BM∥平面AQC.
所以当点M是PA的中点时,BM∥平面AQC.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
