二次函数复习课教案下学期]
图片预览

文档简介
1. 二次函数的图象和性质
解析式 y=ax2+bx+c(a≠0)
a a>0 a<0
Δ Δ>0 Δ=0 Δ<0 Δ>0 Δ=0 Δ<0
图象
与x轴交点 2个 1个 0个 2个 1个
c>0时在原点同侧 c<0时在原点两侧 b<0在原点右侧 b>0在原点左侧 c>0时在原点同侧 c<0时在原点两侧 b<0在原点右侧 b>0在原点左侧 0个
与y轴交点(0,c) c>0在y轴正半轴;c=0交点为(0,0);c<0在y轴负半轴
对称轴 在y轴右侧;,y轴;在y轴左侧
增减性 在对称轴左侧,y随x增大而减小在对称轴右侧,y随x增大而增大 在对称轴左侧,y随x增大而增大在对称轴右侧,y随x增大而减小
开口方向 向上 向下
点() x轴下方 x轴上 x轴上方 x轴上方 在x轴上 x轴下方
最值() 有最小值 有最大值
2、 二次函数y=ax2+bx+c(a≠0)的最大值和最小值:
低点,这个最低点的纵坐标y的值即为最小值,
(2)当a<0,抛物线开口向下,它的顶点是图象上的最高点,这个最高点的纵坐标y的值即为最大值,
求二次函数最值的方法有两个:①用图象法;②配方法。
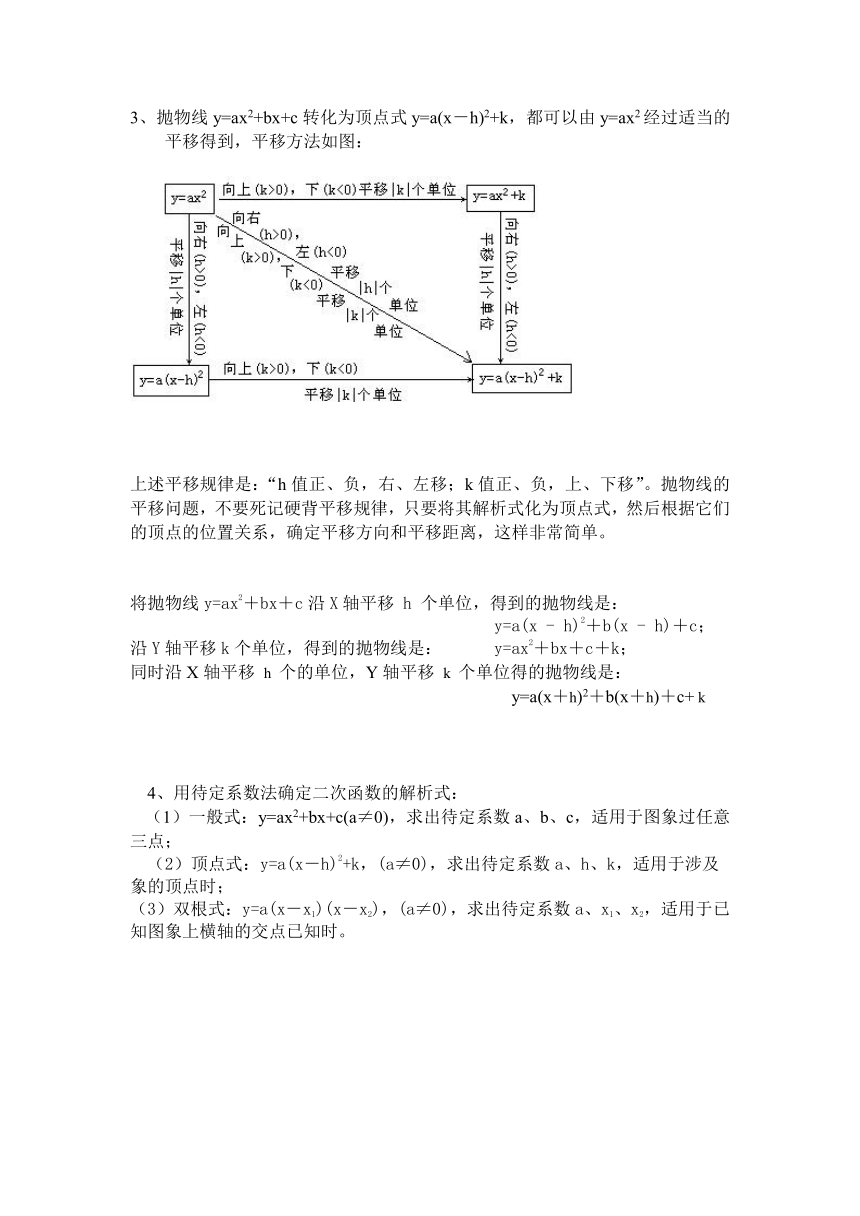
3、抛物线y=ax2+bx+c转化为顶点式y=a(x-h)2+k,都可以由y=ax2经过适当的平移得到,平移方法如图:
上述平移规律是:“h值正、负,右、左移;k值正、负,上、下移”。抛物线的平移问题,不要死记硬背平移规律,只要将其解析式化为顶点式,然后根据它们的顶点的位置关系,确定平移方向和平移距离,这样非常简单。
将抛物线y=ax2+bx+c沿X轴平移 h 个单位,得到的抛物线是:
y=a(x - h)2+b(x - h)+c;
沿Y轴平移k个单位,得到的抛物线是: y=ax2+bx+c+k;
同时沿X轴平移 h 个的单位,Y轴平移 k 个单位得的抛物线是:
y=a(x+h)2+b(x+h)+c+ k
4、用待定系数法确定二次函数的解析式:
(1)一般式:y=ax2+bx+c(a≠0),求出待定系数a、b、c,适用于图象过任意三点;
(2)顶点式:y=a(x-h)2+k,(a≠0),求出待定系数a、h、k,适用于涉及
象的顶点时;
(3)双根式:y=a(x-x1)(x-x2),(a≠0),求出待定系数a、x1、x2,适用于已
知图象上横轴的交点已知时。
1、y=x2-1可由下列( )的图象向右平移1个单位,下平移2个单位得到
A、y=(x-1)2+1 B、y=(x+1)2+1 C、y=(x-1)2-3 D、y=(x+1)2+3
2、 把抛物线向左平移3个单位,再向下平移3个单位,得到的新图象的解析式为( )
3、直角坐标平面上将二次函数y=-2(x-1)2-2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )
A.(0,0) B.(1,-2) C.(0,-1) D.(-2,1)
4、由y=2x2和y=2x2+4x-5的顶点坐标和二次项系数可以得出y=2x2+4x-5的图象可由y=2x2的图象向__________平移________个单位,再向_______平移______个单位得到。
5、抛物线y=x2向上平移2个单位长度后得到新抛物线的解析式为____________。
6、已知y=(k2-k) x2+kx 是二次函数,则k必须满足的条件是_____________________。
7、已知直线y=2x-1 与两个坐标轴的交点是A、B,把y=2x2平移后经过A、B两点,则平移后的二次函数解析式为____________________
8、(1)设抛物线y=2x2,把它向右平移p个单位,或向下移q个单位,都能使得抛物线与直线y=x-4恰好有一个交点,求p,q的值.
(2)把抛物线y=2x2向左平移p个单位,向上平移q个单位,则得到的抛物线经过点(1,3)与(4,9),求p,q的值.
(3)把抛物线y=ax2+bx+c向左平移三个单位,向下平移两个单位析式.
1、 据下列条件求关于x的二次函数的解析式
(1) 当x=3时,y最小值=-1,且图象过(0,7)
(2) 图象过点(0,-2)(1,2)且对称轴为直线x=
(3) 图象经过(0,1)(1,0)(3,0)
(4) 当x=1时,y=0;x=0时,y= -2,x=2 时,y=3
(5) 抛物线顶点坐标为(-1,-2)且通过点(1,10)
2、 物线y= (k2-2)x2+m-4kx的对称轴是直线x=2,且它的最低点在直线y= -+2上,求函数解析式。
3、 二次函数图象与x轴交点的横坐标分别是x1= -3,x2=1时,且与y轴交点为(0,-2),求这个二次函数的解析式
4、已知二次函数的图象顶点是(-1,2),且经过(1,-3),求这个二次函数。
5、y= -x2+2(k-1)x+2k-k2,它的图象经过原点,求①解析式 ②与x轴交点O、A及顶点C组成的△OAC面积。
解析式 y=ax2+bx+c(a≠0)
a a>0 a<0
Δ Δ>0 Δ=0 Δ<0 Δ>0 Δ=0 Δ<0
图象
与x轴交点 2个 1个 0个 2个 1个
c>0时在原点同侧 c<0时在原点两侧 b<0在原点右侧 b>0在原点左侧 c>0时在原点同侧 c<0时在原点两侧 b<0在原点右侧 b>0在原点左侧 0个
与y轴交点(0,c) c>0在y轴正半轴;c=0交点为(0,0);c<0在y轴负半轴
对称轴 在y轴右侧;,y轴;在y轴左侧
增减性 在对称轴左侧,y随x增大而减小在对称轴右侧,y随x增大而增大 在对称轴左侧,y随x增大而增大在对称轴右侧,y随x增大而减小
开口方向 向上 向下
点() x轴下方 x轴上 x轴上方 x轴上方 在x轴上 x轴下方
最值() 有最小值 有最大值
2、 二次函数y=ax2+bx+c(a≠0)的最大值和最小值:
低点,这个最低点的纵坐标y的值即为最小值,
(2)当a<0,抛物线开口向下,它的顶点是图象上的最高点,这个最高点的纵坐标y的值即为最大值,
求二次函数最值的方法有两个:①用图象法;②配方法。
3、抛物线y=ax2+bx+c转化为顶点式y=a(x-h)2+k,都可以由y=ax2经过适当的平移得到,平移方法如图:
上述平移规律是:“h值正、负,右、左移;k值正、负,上、下移”。抛物线的平移问题,不要死记硬背平移规律,只要将其解析式化为顶点式,然后根据它们的顶点的位置关系,确定平移方向和平移距离,这样非常简单。
将抛物线y=ax2+bx+c沿X轴平移 h 个单位,得到的抛物线是:
y=a(x - h)2+b(x - h)+c;
沿Y轴平移k个单位,得到的抛物线是: y=ax2+bx+c+k;
同时沿X轴平移 h 个的单位,Y轴平移 k 个单位得的抛物线是:
y=a(x+h)2+b(x+h)+c+ k
4、用待定系数法确定二次函数的解析式:
(1)一般式:y=ax2+bx+c(a≠0),求出待定系数a、b、c,适用于图象过任意三点;
(2)顶点式:y=a(x-h)2+k,(a≠0),求出待定系数a、h、k,适用于涉及
象的顶点时;
(3)双根式:y=a(x-x1)(x-x2),(a≠0),求出待定系数a、x1、x2,适用于已
知图象上横轴的交点已知时。
1、y=x2-1可由下列( )的图象向右平移1个单位,下平移2个单位得到
A、y=(x-1)2+1 B、y=(x+1)2+1 C、y=(x-1)2-3 D、y=(x+1)2+3
2、 把抛物线向左平移3个单位,再向下平移3个单位,得到的新图象的解析式为( )
3、直角坐标平面上将二次函数y=-2(x-1)2-2的图象向左平移1个单位,再向上平移1个单位,则其顶点为( )
A.(0,0) B.(1,-2) C.(0,-1) D.(-2,1)
4、由y=2x2和y=2x2+4x-5的顶点坐标和二次项系数可以得出y=2x2+4x-5的图象可由y=2x2的图象向__________平移________个单位,再向_______平移______个单位得到。
5、抛物线y=x2向上平移2个单位长度后得到新抛物线的解析式为____________。
6、已知y=(k2-k) x2+kx 是二次函数,则k必须满足的条件是_____________________。
7、已知直线y=2x-1 与两个坐标轴的交点是A、B,把y=2x2平移后经过A、B两点,则平移后的二次函数解析式为____________________
8、(1)设抛物线y=2x2,把它向右平移p个单位,或向下移q个单位,都能使得抛物线与直线y=x-4恰好有一个交点,求p,q的值.
(2)把抛物线y=2x2向左平移p个单位,向上平移q个单位,则得到的抛物线经过点(1,3)与(4,9),求p,q的值.
(3)把抛物线y=ax2+bx+c向左平移三个单位,向下平移两个单位析式.
1、 据下列条件求关于x的二次函数的解析式
(1) 当x=3时,y最小值=-1,且图象过(0,7)
(2) 图象过点(0,-2)(1,2)且对称轴为直线x=
(3) 图象经过(0,1)(1,0)(3,0)
(4) 当x=1时,y=0;x=0时,y= -2,x=2 时,y=3
(5) 抛物线顶点坐标为(-1,-2)且通过点(1,10)
2、 物线y= (k2-2)x2+m-4kx的对称轴是直线x=2,且它的最低点在直线y= -+2上,求函数解析式。
3、 二次函数图象与x轴交点的横坐标分别是x1= -3,x2=1时,且与y轴交点为(0,-2),求这个二次函数的解析式
4、已知二次函数的图象顶点是(-1,2),且经过(1,-3),求这个二次函数。
5、y= -x2+2(k-1)x+2k-k2,它的图象经过原点,求①解析式 ②与x轴交点O、A及顶点C组成的△OAC面积。
