二次函数4[下学期]
图片预览





文档简介
课件15张PPT。第26章 二次函数
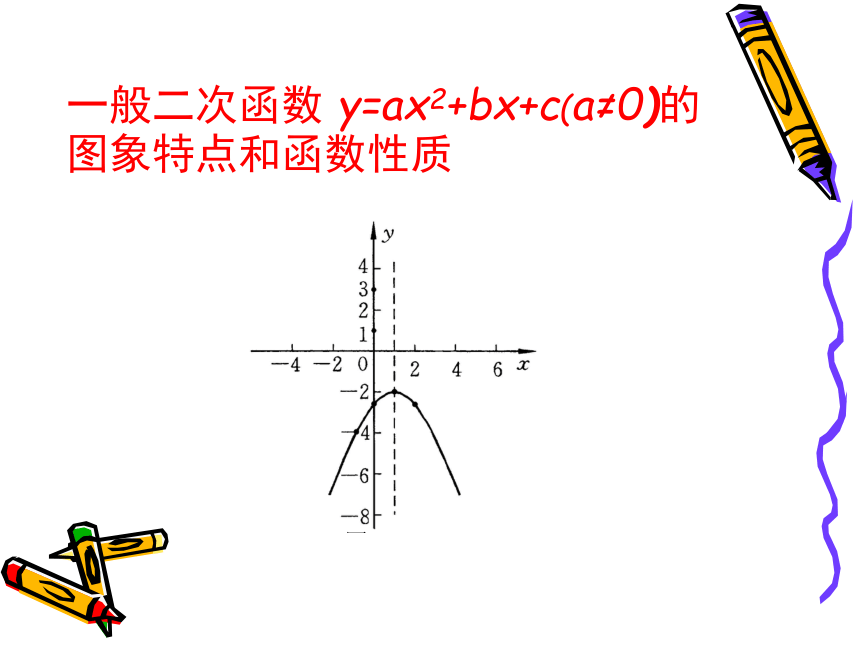
(4)一般二次函数 y=ax2+bx+c(a≠0)的图象特点和函数性质
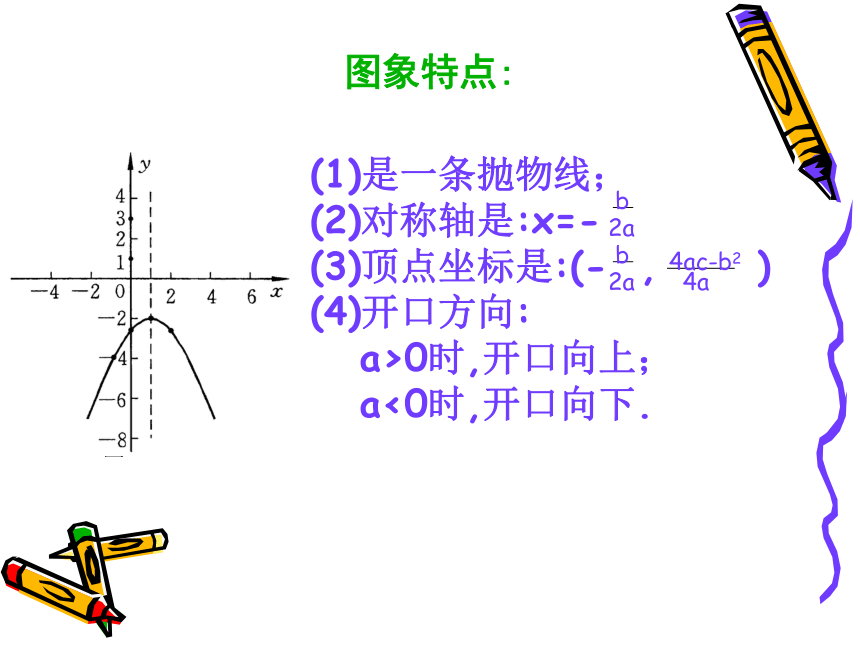
(1)是一条抛物线;
(2)对称轴是:x=-
(3)顶点坐标是:(- , )
(4)开口方向:
a>0时,开口向上;
a<0时,开口向下.
图象特点:
(1) a>0时,对称轴左侧(x<- ),函数值y随x的增大而减小 ;对称轴右侧(x>- ),函数值y随x的增大而增大 。
a<0时,对称轴左侧(x<- ),函数值y随x的增大而增大 ;对称轴右侧(x>- ),函数值y随x的增大而减小 。
(2) a>0时,ymin=
a<0时,ymax=
函数性质:在连线时,在起始点和结束点还要沿函数图象的趋势向外延长一部分。
二次函数的图象解:列表小结
由此可知画二次函数图象的一般步骤是:
1、取值列表;
2、描点连线。
在此过程中需要注意的有:
1、自变量取值间隔要一致,通常取5或7个值;
2、在起始点和终点函数图象还要沿着函数图象
的趋势延长一部分;
3、函数图象要能够反映出函数的整体变化情况。
思考:如何求出以上函数
y=x2-2x-1的图像与x轴、y轴的交点的坐标
(1)与x轴的交点的坐标求法:当?=0时,求出. . .
(2)与y轴的交点的坐标求法:当?=0时,求出. . .
(1)抛物线y=-2x2+5x-3与y轴交于点C,与x轴的交点A、B,
A在B的左边,求这三点坐标. (2)抛物线y=x2-3x+2与y轴交于点C,与x轴的交点A、B,求△ABC的面积。抛物线y=x2+x+1与y轴的交点坐标是__________,与x轴的交点坐标是______思考:抛物线y=ax2+bx+c与x轴交点个数由什么因素决定?与x轴交点横坐标x1,2=下列抛物线与坐标轴各有几个交点 (1).y=2x2+4x-8
(2).y=2x2-8x+9
(3).y=2x2+4x+2
(4).y=3x2
(5).y=2x2+2
(6).y=2x2 – 2x
抛物线y=ax2+bx+c与x轴轴交于A、B,用a、b、c的代数式表示AB的长度。 抛物线y=ax2+bx+c与x轴交于A、B,与y 轴的交点C,用a、b、c的代数式表示△ABC的面积。 用五点法画函数y=0.5x2+2X的图象 抛物线y=-0.5x2-7x+7.5与x轴交于A、B,与y 轴的交点C, C关于图像对称轴的对称点为D,顶点为E。
(1)求这五点的坐标。
(2)用五点法画图像。 抛物线y=ax2+bx+c,用a、b、c的代数式表示以上五点 已知A、B两点的横坐标为x1、x2,
求抛物线的对称轴。已知抛物线过(m,p)和(n,p),求抛物线的对称轴。抛物线y=2(x-1)(x-3)与y轴交于点C,与x轴的交点A、B,
A在B的左边,求这三点坐标.抛物线y=a(x-m)(x-n)与y轴交于点C(0,6),与x轴的交点A(1,0)、B(3,0),求抛物线的解析式.抛物线y=ax2+bx+c经过(2,0),(-6,0)两点,函数最小值是3,求抛物线的解析式.抛物线过(2,1),对称轴x=2,与x轴两交点间距离为6,求抛物线解析式. 已知抛物线过(2,6)和(1,4)且与x轴两交点距离为5,求抛物线解析式。抛物线y=2x2+6x向下平移若干个单位,得到的新抛物线与x轴截得线段长为5,求新抛物线解析式。
(4)一般二次函数 y=ax2+bx+c(a≠0)的图象特点和函数性质
(1)是一条抛物线;
(2)对称轴是:x=-
(3)顶点坐标是:(- , )
(4)开口方向:
a>0时,开口向上;
a<0时,开口向下.
图象特点:
(1) a>0时,对称轴左侧(x<- ),函数值y随x的增大而减小 ;对称轴右侧(x>- ),函数值y随x的增大而增大 。
a<0时,对称轴左侧(x<- ),函数值y随x的增大而增大 ;对称轴右侧(x>- ),函数值y随x的增大而减小 。
(2) a>0时,ymin=
a<0时,ymax=
函数性质:在连线时,在起始点和结束点还要沿函数图象的趋势向外延长一部分。
二次函数的图象解:列表小结
由此可知画二次函数图象的一般步骤是:
1、取值列表;
2、描点连线。
在此过程中需要注意的有:
1、自变量取值间隔要一致,通常取5或7个值;
2、在起始点和终点函数图象还要沿着函数图象
的趋势延长一部分;
3、函数图象要能够反映出函数的整体变化情况。
思考:如何求出以上函数
y=x2-2x-1的图像与x轴、y轴的交点的坐标
(1)与x轴的交点的坐标求法:当?=0时,求出. . .
(2)与y轴的交点的坐标求法:当?=0时,求出. . .
(1)抛物线y=-2x2+5x-3与y轴交于点C,与x轴的交点A、B,
A在B的左边,求这三点坐标. (2)抛物线y=x2-3x+2与y轴交于点C,与x轴的交点A、B,求△ABC的面积。抛物线y=x2+x+1与y轴的交点坐标是__________,与x轴的交点坐标是______思考:抛物线y=ax2+bx+c与x轴交点个数由什么因素决定?与x轴交点横坐标x1,2=下列抛物线与坐标轴各有几个交点 (1).y=2x2+4x-8
(2).y=2x2-8x+9
(3).y=2x2+4x+2
(4).y=3x2
(5).y=2x2+2
(6).y=2x2 – 2x
抛物线y=ax2+bx+c与x轴轴交于A、B,用a、b、c的代数式表示AB的长度。 抛物线y=ax2+bx+c与x轴交于A、B,与y 轴的交点C,用a、b、c的代数式表示△ABC的面积。 用五点法画函数y=0.5x2+2X的图象 抛物线y=-0.5x2-7x+7.5与x轴交于A、B,与y 轴的交点C, C关于图像对称轴的对称点为D,顶点为E。
(1)求这五点的坐标。
(2)用五点法画图像。 抛物线y=ax2+bx+c,用a、b、c的代数式表示以上五点 已知A、B两点的横坐标为x1、x2,
求抛物线的对称轴。已知抛物线过(m,p)和(n,p),求抛物线的对称轴。抛物线y=2(x-1)(x-3)与y轴交于点C,与x轴的交点A、B,
A在B的左边,求这三点坐标.抛物线y=a(x-m)(x-n)与y轴交于点C(0,6),与x轴的交点A(1,0)、B(3,0),求抛物线的解析式.抛物线y=ax2+bx+c经过(2,0),(-6,0)两点,函数最小值是3,求抛物线的解析式.抛物线过(2,1),对称轴x=2,与x轴两交点间距离为6,求抛物线解析式. 已知抛物线过(2,6)和(1,4)且与x轴两交点距离为5,求抛物线解析式。抛物线y=2x2+6x向下平移若干个单位,得到的新抛物线与x轴截得线段长为5,求新抛物线解析式。
