18.4 反比例函数的图象和性质[下学期]
文档属性
| 名称 | 18.4 反比例函数的图象和性质[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 381.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-05 12:26:00 | ||
图片预览






文档简介
课件31张PPT。反比例函数的图象和性质反比例函数的定义问题1:当矩形面积为6时,长a
与宽b成的关系是
问题2:当路程s一定时,时间t
与速度v的关系是反比例函数的定义函数 (k是常数,k≠0)叫
做反比例函数.也可以写成y=kx -1的形式.其中自变量X和函数值Y的取值范围是反比例函数的图象(可以。)( 我们先研究一次函数的定义,再研究
一次函数图象的画法,最后研究一次函数
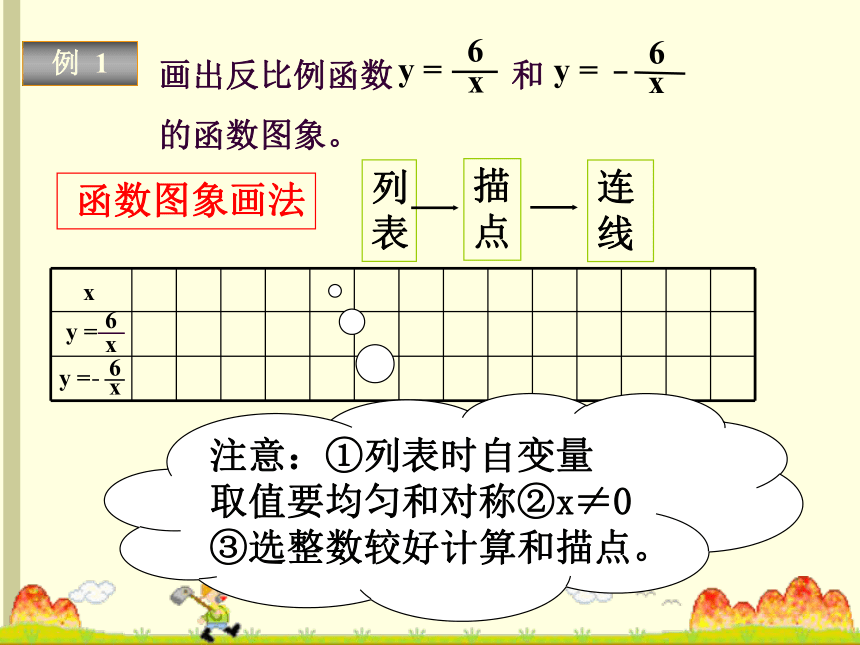
的性质。) 函数图象画法列
表描
点连
线注意:①列表时自变量
取值要均匀和对称②x≠0
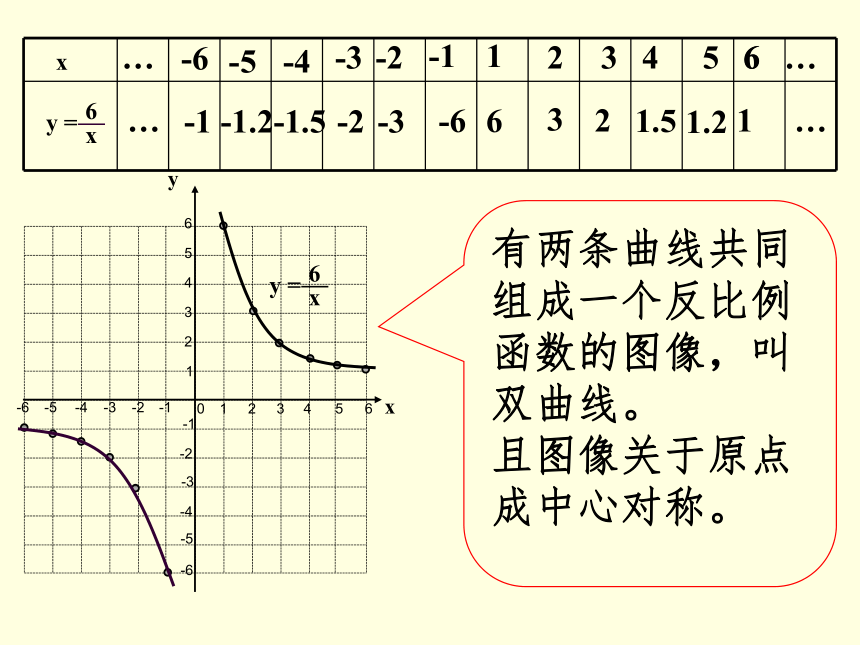
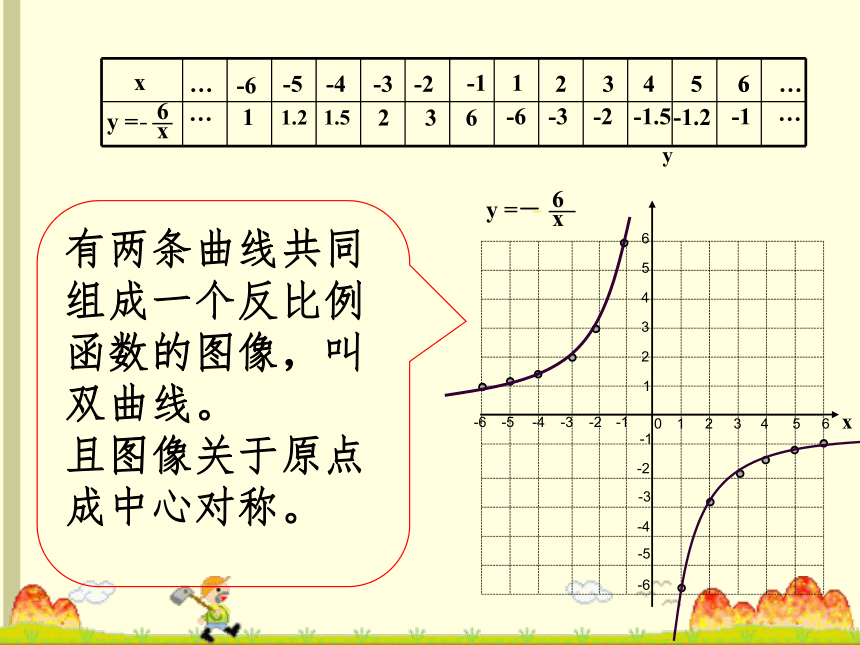
③选整数较好计算和描点。例 1123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………有两条曲线共同组成一个反比例函数的图像,叫双曲线。 且图像关于原点成中心对称。123456-1-3-2-4-5-61234-1-2-3-40-6-556yx1234566-1-2-3-4-5-6……-663-32-21.5-1.51.2-1.21-1……有两条曲线共同组成一个反比例函数的图像,叫双曲线。 且图像关于原点成中心对称。 讨 论①当k>0时,双曲线两分支各在哪个象限?在每个象限内,随着自变量x的增大,函数值y如何变化?请大家结合反比例函数
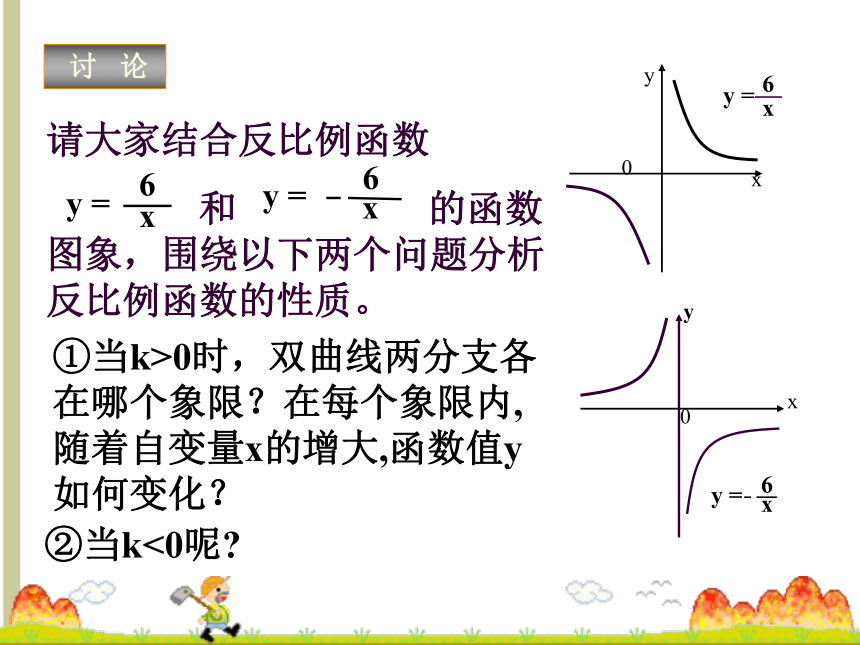
和 的函数图象,围绕以下两个问题分析反比例函数的性质。 0②当k<0呢?yx0123456123456反比例函数的图象
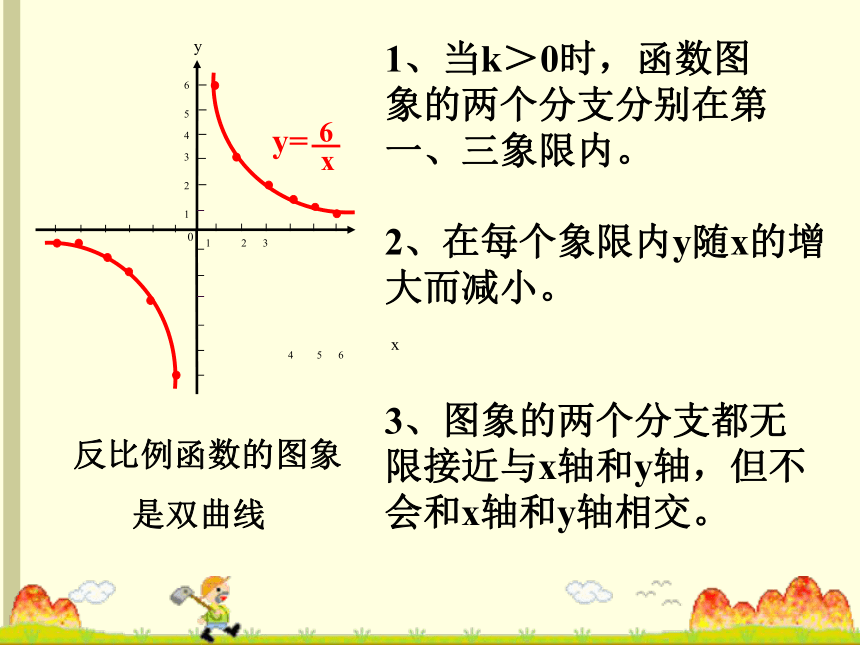
是双曲线1、当k>0时,函数图象的两个分支分别在第一、三象限内。2、在每个象限内y随x的增大而减小。3、图象的两个分支都无限接近与x轴和y轴,但不会和x轴和y轴相交。反比例函数的图象
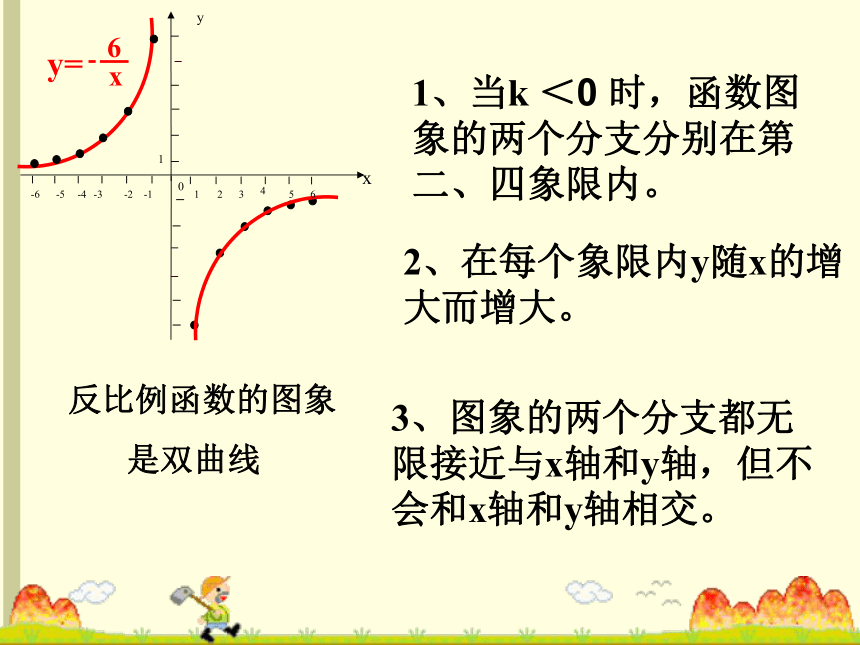
是双曲线1、当k <0 时,函数图象的两个分支分别在第二、四象限内。2、在每个象限内y随x的增大而增大。3、图象的两个分支都无限接近与x轴和y轴,但不会和x轴和y轴相交。反比例函数的性质1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,y随x的增大而减小;
2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,y随x的增大而增大。
0位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 y随x的增大而减小二四象限二四象限 y随x的增大而减小 y随x的增大而增大
填表分析正比例函数和反比例函数的区别随堂练习
例1:已知反比例函数y=mxm2-5 ,它的两个分支分别在第一、第三象限,求m的值?
得 m =2
对于 - ,当x<0时,y__0,这部分图象在第__象限.
练习11.对于函数 ,当x>0时,
y__0,这部分图象在第__象限;
>一>二2、若函数 的图象在第一、三象限,
则实数m的取值范围是_____________。练习13.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________k>-14.甲乙两地相距100km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )C在实际问题中图象就可能只有一支.练习15.已知反比例函数 的图象
在 第二、四象限,那么一次函数y=kx-k的图象经过( )A 第一、二、三象限 B 第一、二、四象限
C 第一、三、四象限 D 第二、三、四象限Ck>0练习16、已知y 与 x 成反比例, 并且当 x = 3 时y = 7,求 x 与 y 的函数关系式。 7、根据图形写出函数的解析式。 反比例函数的性质2(X1,y1)O2.双曲线关于原点对称1. Ek=xy反比例函数的性质2(X1,y1)O3.
ES?OAB=1.双曲线 经过点(3,a),则a=______.
2.双曲线 上有一点(3,- 4),则k=______.练习21/9-12练习23.若函数 的图象过点(3,-7),那么它一定还经过点 .
A.(3,7) B.(-3,-7)
C.(-3,7) D.(2,-7)
C练习24.如图,Rt△AOB的顶点A在双曲线 上,且S△AOB=3,求m的值. ∵ S△AOB =1/2m=3∴ m=6 已知y与x2成反比例,并且当x=3时,y=4,求当x=1.5时y的值.
?解:设y=k / x2 ∵x=3时,y=4 ∴4=k/9
∴k=36
当x=1.5时,
y=36/x2 =36/(1.5)2 =16
例 2练习31.已知反比例函数的图象经过点(-3,6),求解析式.2.一次函数和反比例函数的一个交点是(2,3),另外,一次函数又经过点(0,-1),求这两个函数的解析式.练习33.面积为3的矩形OABC的一个顶点B在反比例函数 的图象上,
另3个点在坐标轴上,则函数解析式是______. BCOAy=-3/x小结12作业:习题17.4 A组
第1 、2题再见!
与宽b成的关系是
问题2:当路程s一定时,时间t
与速度v的关系是反比例函数的定义函数 (k是常数,k≠0)叫
做反比例函数.也可以写成y=kx -1的形式.其中自变量X和函数值Y的取值范围是反比例函数的图象(可以。)( 我们先研究一次函数的定义,再研究
一次函数图象的画法,最后研究一次函数
的性质。) 函数图象画法列
表描
点连
线注意:①列表时自变量
取值要均匀和对称②x≠0
③选整数较好计算和描点。例 1123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………有两条曲线共同组成一个反比例函数的图像,叫双曲线。 且图像关于原点成中心对称。123456-1-3-2-4-5-61234-1-2-3-40-6-556yx1234566-1-2-3-4-5-6……-663-32-21.5-1.51.2-1.21-1……有两条曲线共同组成一个反比例函数的图像,叫双曲线。 且图像关于原点成中心对称。 讨 论①当k>0时,双曲线两分支各在哪个象限?在每个象限内,随着自变量x的增大,函数值y如何变化?请大家结合反比例函数
和 的函数图象,围绕以下两个问题分析反比例函数的性质。 0②当k<0呢?yx0123456123456反比例函数的图象
是双曲线1、当k>0时,函数图象的两个分支分别在第一、三象限内。2、在每个象限内y随x的增大而减小。3、图象的两个分支都无限接近与x轴和y轴,但不会和x轴和y轴相交。反比例函数的图象
是双曲线1、当k <0 时,函数图象的两个分支分别在第二、四象限内。2、在每个象限内y随x的增大而增大。3、图象的两个分支都无限接近与x轴和y轴,但不会和x轴和y轴相交。反比例函数的性质1.当k>0时,图象的两个分支分别在第一、三象限内,在每个象限内,y随x的增大而减小;
2.当k<0时,图象的两个分支分别在第二、四象限内,在每个象限内,y随x的增大而增大。
0位置增减性位置增减性y=kx ( k≠0 ) 直线 双曲线一三象限 y随x的增大而增大一三象限 y随x的增大而减小二四象限二四象限 y随x的增大而减小 y随x的增大而增大
填表分析正比例函数和反比例函数的区别随堂练习
例1:已知反比例函数y=mxm2-5 ,它的两个分支分别在第一、第三象限,求m的值?
得 m =2
对于 - ,当x<0时,y__0,这部分图象在第__象限.
练习11.对于函数 ,当x>0时,
y__0,这部分图象在第__象限;
>一>二2、若函数 的图象在第一、三象限,
则实数m的取值范围是_____________。练习13.若关于x,y的函数 图象位于第一、三象限,
则k的取值范围是_______________k>-14.甲乙两地相距100km,一辆汽车从甲地开往乙地,
把汽车到达乙地所用的时间y(h)表示为汽车的平均
速度x(km/h)的函数,则这个函数的图象大致是( )C在实际问题中图象就可能只有一支.练习15.已知反比例函数 的图象
在 第二、四象限,那么一次函数y=kx-k的图象经过( )A 第一、二、三象限 B 第一、二、四象限
C 第一、三、四象限 D 第二、三、四象限Ck>0练习16、已知y 与 x 成反比例, 并且当 x = 3 时y = 7,求 x 与 y 的函数关系式。 7、根据图形写出函数的解析式。 反比例函数的性质2(X1,y1)O2.双曲线关于原点对称1. Ek=xy反比例函数的性质2(X1,y1)O3.
ES?OAB=1.双曲线 经过点(3,a),则a=______.
2.双曲线 上有一点(3,- 4),则k=______.练习21/9-12练习23.若函数 的图象过点(3,-7),那么它一定还经过点 .
A.(3,7) B.(-3,-7)
C.(-3,7) D.(2,-7)
C练习24.如图,Rt△AOB的顶点A在双曲线 上,且S△AOB=3,求m的值. ∵ S△AOB =1/2m=3∴ m=6 已知y与x2成反比例,并且当x=3时,y=4,求当x=1.5时y的值.
?解:设y=k / x2 ∵x=3时,y=4 ∴4=k/9
∴k=36
当x=1.5时,
y=36/x2 =36/(1.5)2 =16
例 2练习31.已知反比例函数的图象经过点(-3,6),求解析式.2.一次函数和反比例函数的一个交点是(2,3),另外,一次函数又经过点(0,-1),求这两个函数的解析式.练习33.面积为3的矩形OABC的一个顶点B在反比例函数 的图象上,
另3个点在坐标轴上,则函数解析式是______. BCOAy=-3/x小结12作业:习题17.4 A组
第1 、2题再见!
