18.4 反比例函数[下学期]
图片预览





文档简介
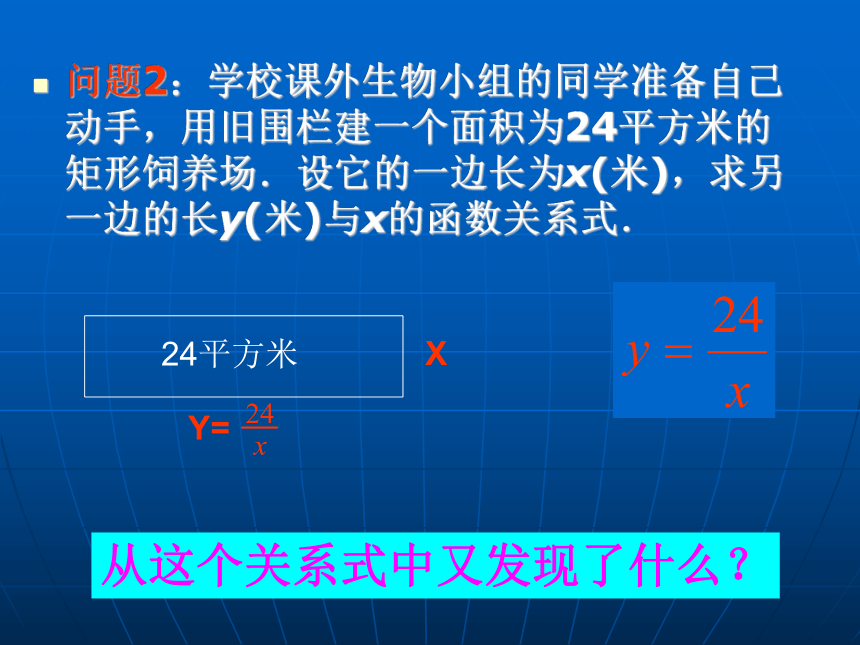
课件15张PPT。反比例函数创设情境 回顾小学所学反比例关系。 两个相关联的量,一个量变化,另一个量也随着变化,如果两个数的积一定,这两个数的关系叫做反比例关系.探究归纳 问题1 小华的爸爸早晨骑自行车带小华到15千米的镇外去赶集,回来时让小华乘公共汽车,用的时间少了.假设两人经过的路程一样,而且自行车和汽车的速度在行驶过程中都不变,爸爸要小华找出从家里到镇上的时间和乘坐不同交通工具的速度之间的关系. 设小华乘坐交通工具的速度是v 千米/时,从家里到镇上的时间是t 小时.因为在匀速运动中,时间=路程÷速度,所以 从这个关系式中发现了什么?问题2:学校课外生物小组的同学准备自己动手,用旧围栏建一个面积为24平方米的矩形饲养场.设它的一边长为x(米),求另一边的长y(米)与x的函数关系式.从这个关系式中又发现了什么?24平方米XY=上述两个函数都具有 的形式,一般
地,形如 (k是常数,k≠0)的函
数叫做反比例函数. 上述两个函数表达式都具有什么特点?解:因为平行四边形被其对角线分成两个面积相等的三角形.
而三角形的面积=
即:2×
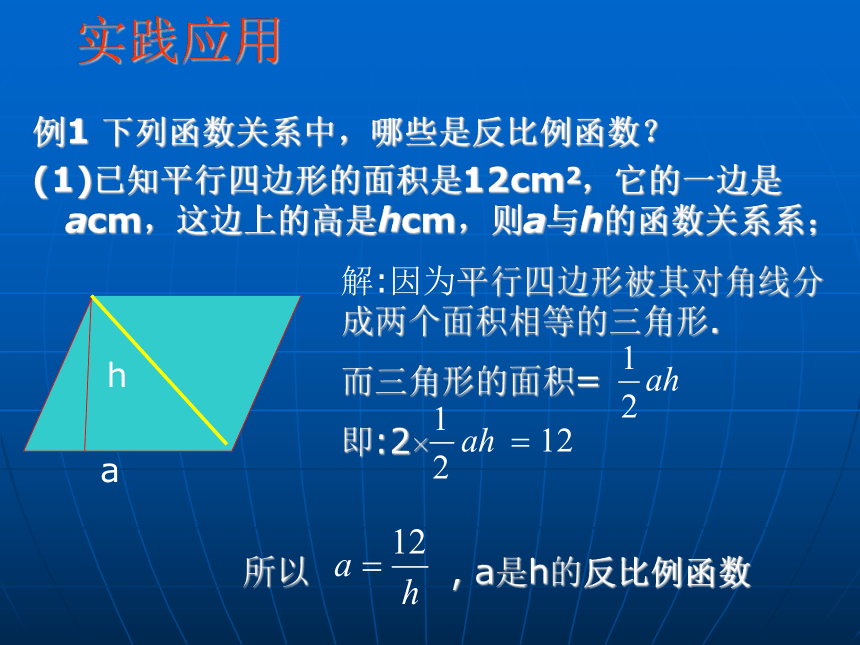
实践应用 例1 下列函数关系中,哪些是反比例函数?
(1)已知平行四边形的面积是12cm2,它的一边是acm,这边上的高是hcm,则a与h的函数关系系; ah所以 , a是h的反比例函数(2)压强p一定时,压力F与受力面积s的关系;(3)某乡粮食总产量为种种原因 m 吨,那么该乡每人平
均拥有粮食 y (吨)与该乡人口数 x 的函数关系式.Y是x的反比例函数F=ps F是s的正比例函数例2 已知y与x成反比例,并且当x=3时,y=2.求x=1.5时y的值. 解:设 . 由题意有
即 k =6. 因此 所以,当x=1.5时还记得这叫什么方法吗?解:因为函数 是反比例函数
有 2m-2=1. 即
例3 当m为何值时,函数 是反比
例函数,并求出其函数解析式.所以当 时, 是反比例函数1、下列函数中,哪些是反比例函数?说出反比例函数的比例系数 (1)y = -3x; (2)y = 2x+1; (3) ;
(4)y =3(x-1)2+1;(5) (s是常数,s≠0)(6) ;(7) ;练习2.列出下列问题中的函数关系式,并指出它们是什么函数:
(1)三角形的面积S是常数时,它的底边长y和这条底上的高x的函数关系;
(3).某厂现在年产值是150万元,计划今后每年增加10万元,请写出年产值y(万元)与年数x之间的关系.y是x的反比例函数(2)食堂存煤15吨,可使用的天数t和平均每天的用煤
量Q(千克)的函数关系.t是Q的反比例函数y=150+10xy是x的一次函数3、解答下列问题:
(1)y是x的反比例函数,当x=2时,y=3,求y与x之间的函数关系式。
(2)若y与x成正比例,x与z成反比例,则y与t成什么关系?
(3)已知y1与x成正比,y2与x成反比,且y=y1+y2。当x=1时y=3;当x=2时y=3。求y与x之间的函数关系式。5.某人在银行的信用卡中存入2万元,每次取出50元,若卡内余钱为y(元),取钱的次数为x(利息忽略不计):
(1)写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)取多少次钱后,余额为原存款额的四分之一?4.已知y与x-2成反比例,当x=4时, y=3,求当x=5时,y的值.y=20000-50x0≤x≤400300次小结 1.本堂课,我们讨论了具有什么样的函数是反比例
函数,一般地,形如 (k是常数,k≠0)
的函数叫做反比例函数
2.要求反比例函数的解析式,可通过待定系数法求出k值,即可确定.再见作业:教材第50页练习第1,2题
地,形如 (k是常数,k≠0)的函
数叫做反比例函数. 上述两个函数表达式都具有什么特点?解:因为平行四边形被其对角线分成两个面积相等的三角形.
而三角形的面积=
即:2×
实践应用 例1 下列函数关系中,哪些是反比例函数?
(1)已知平行四边形的面积是12cm2,它的一边是acm,这边上的高是hcm,则a与h的函数关系系; ah所以 , a是h的反比例函数(2)压强p一定时,压力F与受力面积s的关系;(3)某乡粮食总产量为种种原因 m 吨,那么该乡每人平
均拥有粮食 y (吨)与该乡人口数 x 的函数关系式.Y是x的反比例函数F=ps F是s的正比例函数例2 已知y与x成反比例,并且当x=3时,y=2.求x=1.5时y的值. 解:设 . 由题意有
即 k =6. 因此 所以,当x=1.5时还记得这叫什么方法吗?解:因为函数 是反比例函数
有 2m-2=1. 即
例3 当m为何值时,函数 是反比
例函数,并求出其函数解析式.所以当 时, 是反比例函数1、下列函数中,哪些是反比例函数?说出反比例函数的比例系数 (1)y = -3x; (2)y = 2x+1; (3) ;
(4)y =3(x-1)2+1;(5) (s是常数,s≠0)(6) ;(7) ;练习2.列出下列问题中的函数关系式,并指出它们是什么函数:
(1)三角形的面积S是常数时,它的底边长y和这条底上的高x的函数关系;
(3).某厂现在年产值是150万元,计划今后每年增加10万元,请写出年产值y(万元)与年数x之间的关系.y是x的反比例函数(2)食堂存煤15吨,可使用的天数t和平均每天的用煤
量Q(千克)的函数关系.t是Q的反比例函数y=150+10xy是x的一次函数3、解答下列问题:
(1)y是x的反比例函数,当x=2时,y=3,求y与x之间的函数关系式。
(2)若y与x成正比例,x与z成反比例,则y与t成什么关系?
(3)已知y1与x成正比,y2与x成反比,且y=y1+y2。当x=1时y=3;当x=2时y=3。求y与x之间的函数关系式。5.某人在银行的信用卡中存入2万元,每次取出50元,若卡内余钱为y(元),取钱的次数为x(利息忽略不计):
(1)写出y与x之间的函数关系式;
(2)求出自变量x的取值范围;
(3)取多少次钱后,余额为原存款额的四分之一?4.已知y与x-2成反比例,当x=4时, y=3,求当x=5时,y的值.y=20000-50x0≤x≤400300次小结 1.本堂课,我们讨论了具有什么样的函数是反比例
函数,一般地,形如 (k是常数,k≠0)
的函数叫做反比例函数
2.要求反比例函数的解析式,可通过待定系数法求出k值,即可确定.再见作业:教材第50页练习第1,2题
