18.4 反比例函数[下学期]

课件34张PPT。八年级数学下 反比例函数章节复习定义：形如 （k≠0,k为常数）叫反比例函数。（其中x ≠0,y ≠0)
等价形式：(k ≠0) 概 念y=kx-1xy=ky与x成反比例下列函数中y与x是反比例函数有哪些?

① ②
③ ④

⑤ ⑥
⑦ ⑧
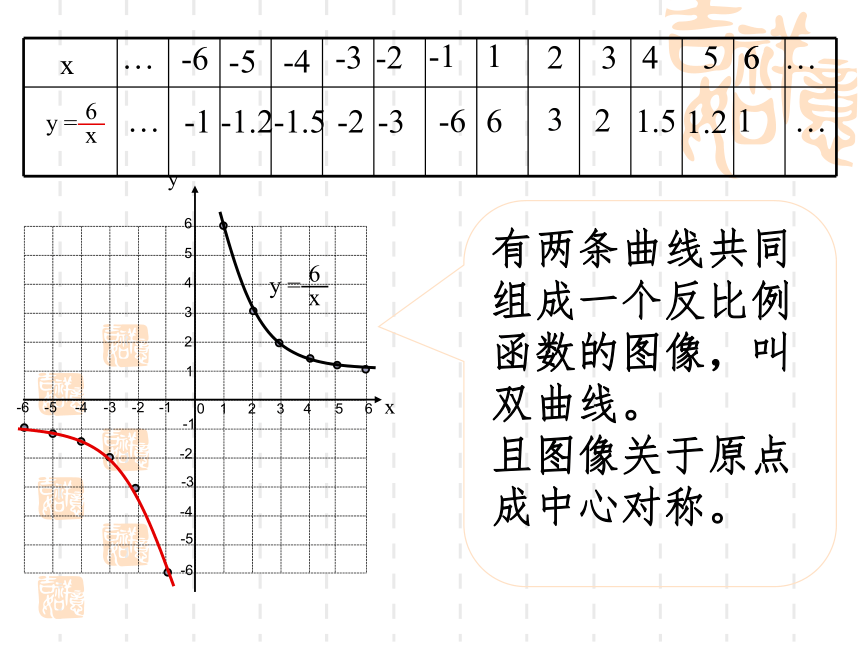
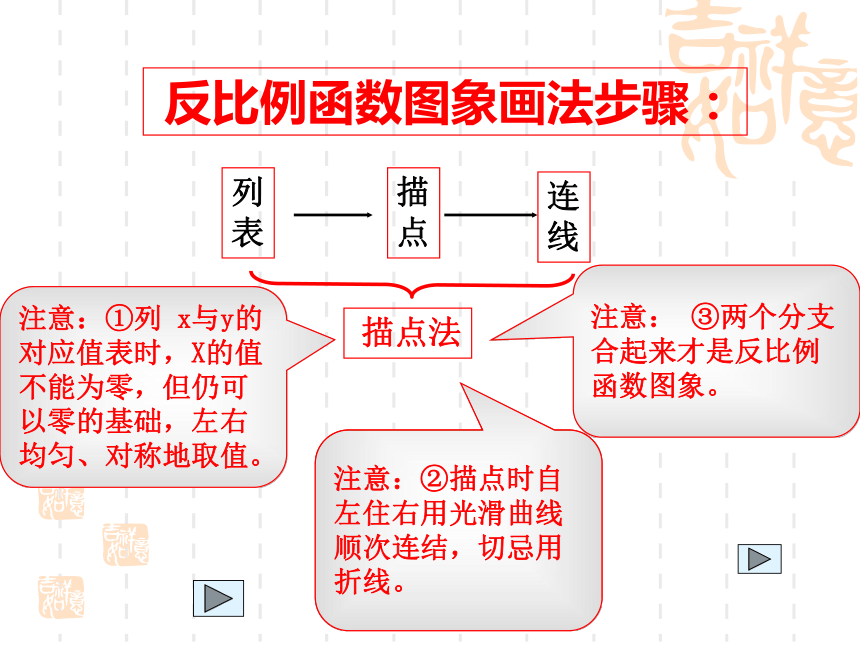
练习一：基本概念y=-x-1x y=02y=x123456-1-3-2-4-5-61234-1-2-3-40-6-556xy16233241.551.2616-1-6-2-3-3-1.5-2-4-5-1.2-6-1…………有两条曲线共同组成一个反比例函数的图像，叫双曲线。且图像关于原点成中心对称。从画反比例函数图象看,描点法还应注意什么? 反比例函数图象画法步骤：列
表描
点连
线 描点法注意：①列 x与y的对应值表时，X的值不能为零，但仍可以零的基础，左右
均匀、对称地取值。注意：②描点时自左住右用光滑曲线顺次连结，切忌用折线。注意： ③两个分支合起来才是反比例函数图象。图像与性质图像
位置
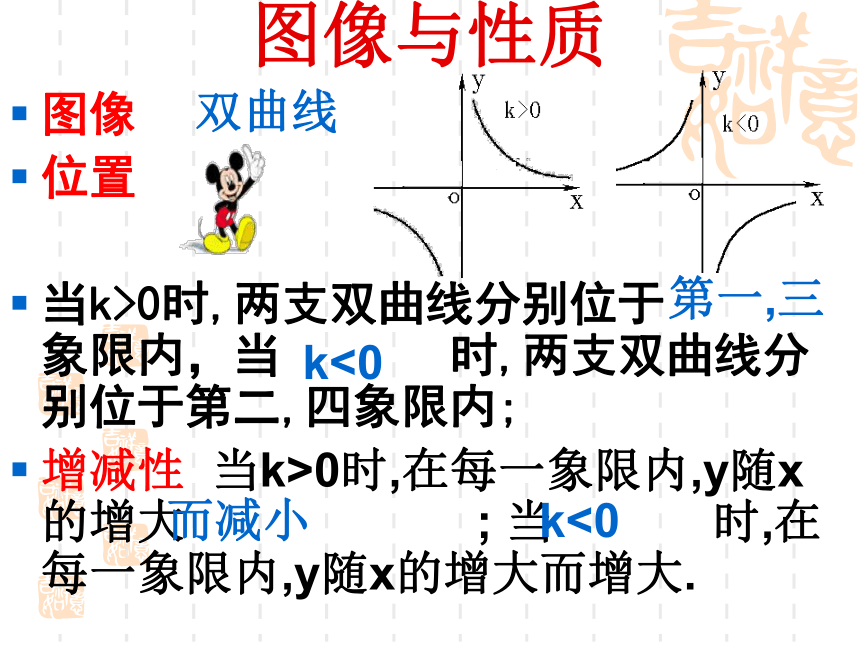
当k>0时,两支双曲线分别位于 象限内，当 时,两支双曲线分别位于第二,四象限内;
增减性 当k>0时,在每一象限内,y随x的增大 ; 当 时,在每一象限内,y随x的增大而增大.双曲线第一,三k<0而减小k<0图像与性质渐近性反比例函数的图象无限接近于
轴,但永远达不到x,y轴,并且︳K︱越 ，图像越接近坐标轴。
对称性 反比例函数的图象是关于原点成 对称的图形.反比例函数的图象也是 对称图形.
面积不变性
长方形面积 ︳mn︱ ＝︳K︱ 小中心轴x,y例1.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .y1＞ y2代入法：
图象法：找出A、B两点的大致位置从而判断y值的大小。2.已知点A(-2,y1),B(-1,y2)
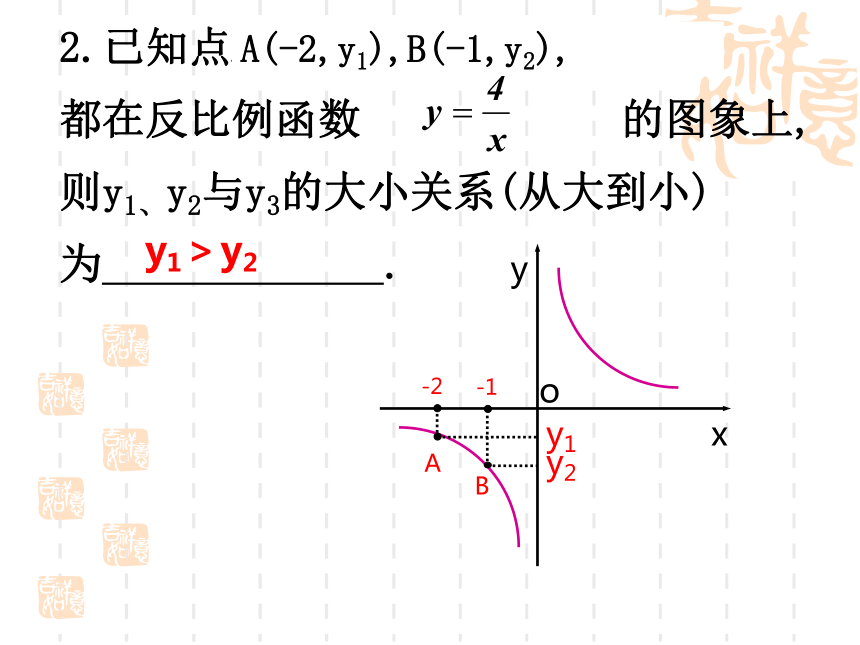
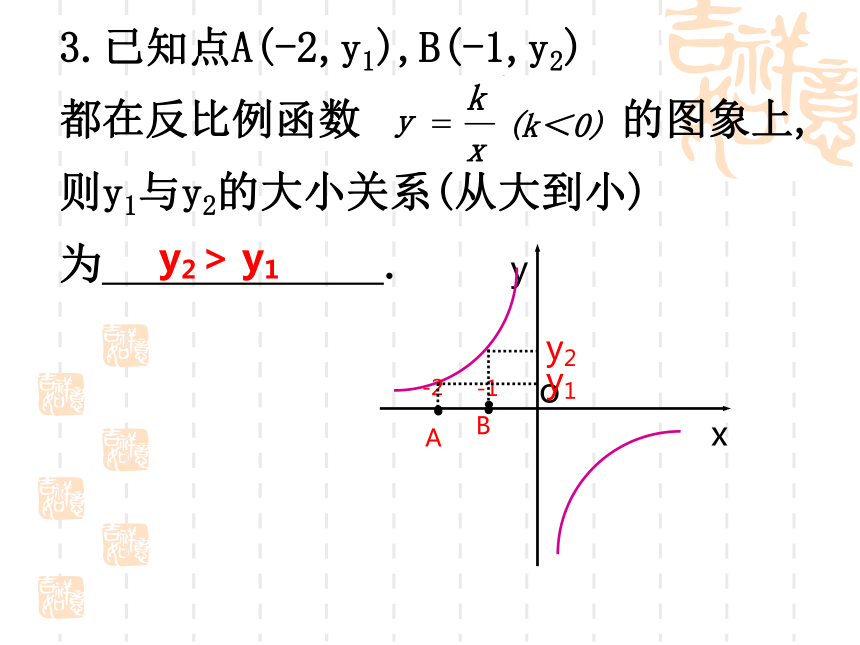
都在反比例函数 的图象上,则y1、y2与y3的大小关系(从大到小)为 .A(-2,y1),B(-1,y2),y1＞y23.已知点A(-2,y1),B(-1,y2)
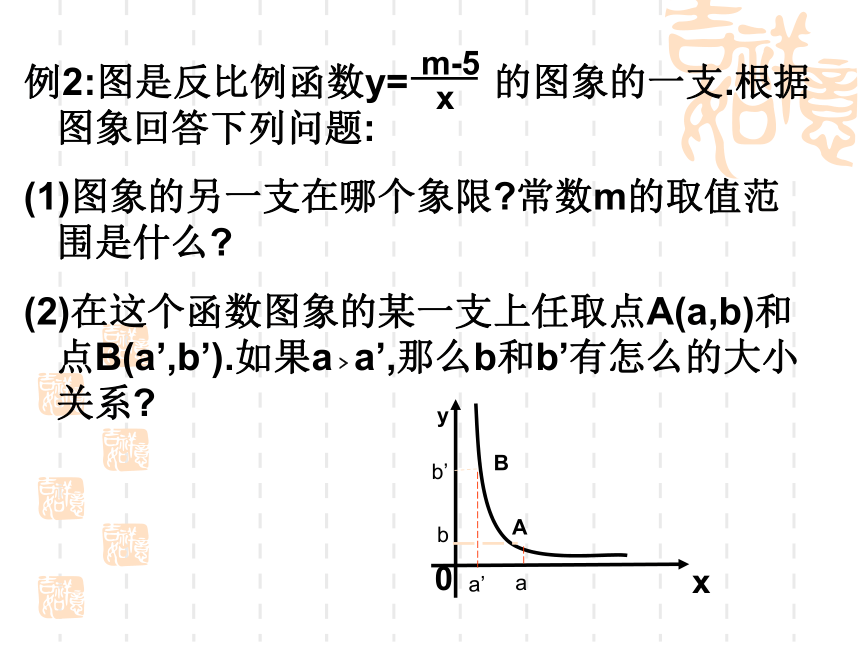
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .y2＞ y1例2:图是反比例函数y= 的图象的一支.根据图象回答下列问题:
图象的另一支在哪个象限?常数m的取值范围是什么?
在这个函数图象的某一支上任取点A(a,b)和点B(a’,b’).如果a﹥a’,那么b和b’有怎么的大小关系?0aa’b’bAB1.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与y2的大小关系(从大到小)为 .y1＞ y22.已知点A(-2,y1),B(-1,y2)
都在反比例函数 的图象上,则y1与

y2的大小关系(从大到小)为 .y2＞ y1y1 ＞0＞y2y3 ＞y1＞y2 考察函数 的图象,当x=-2时,y= ___ ,当x<-2时,y的取值范围是 _____ ;当y﹥-1时,x的取值范围是 _________ .-1-10若点（-2，y1）、（-1，y2）、（2，y3）在
反比例函数 的图象上，则（ ）A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1B做一做1.如图,点P是反比例函数 图象上的一点,PD⊥x轴于D.则△POD的面积为 .(m,n)1练习3、已知反比例函数 ，若
X1 ∴k=±12 X>0待定系数法、交点问题：一、待定系数法
二、交点问题：
1、与坐标轴的交点问题：
无限趋近于x、y轴， 与x、y轴无交点。
2、与正比例函数的交点问题：
最好利用反比例函数的中心对称性。
3、与一次函数的交点问题：
列方程组，求公共解，即交点坐标。例、如图在坐标系中，直线y=x+ k与双曲线 在第一象限交与点A， 与x轴交于点C，AB垂直x轴，垂足为B，
且S△AOB＝1
1）求两个函数解析式
2）求△ABC的面积反比例函数交点问题：超越自我:（05江西省中考题）已知甲,乙两地相距skm,汽车从甲地匀速行驶到乙地.如果汽车每小时耗油量为aL,那么从甲地到乙地的总耗油量y(L)与汽车的行驶速度v(km/h)的函数图象大致是( ).实际应用实际应用超越自我:小结：本节复习课主要复习本章学生应知应会的概念、图像、性质、应用等内容，夯实基础提高应用。
充分利用“图象”这个载体，随时随地渗透数形结合的数学思想.作业练习二：图像与性质1、如图是三个反比例函数在x轴上方的图像， 由此观察得到( )
A k1>k2>k3 B k3>k2>k1
C k2>k1>k3 D k3>k1>k2例：表示下面四个关系式的图像有图像与性质