18.4 反比例函数[下学期]

课件20张PPT。反比例函数(复习课)高邮市赞化学校 俞永亮华师大版教材本节知识结构：反比例函数1.定义2.图象5.应用3.图象的性质4.解析式的求法一、概念： 形如 的函数叫做
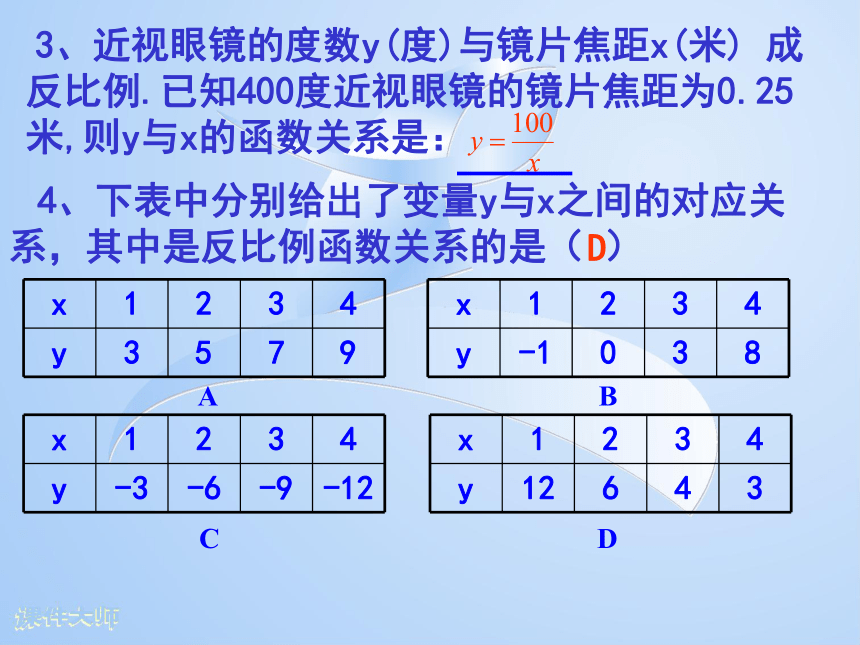
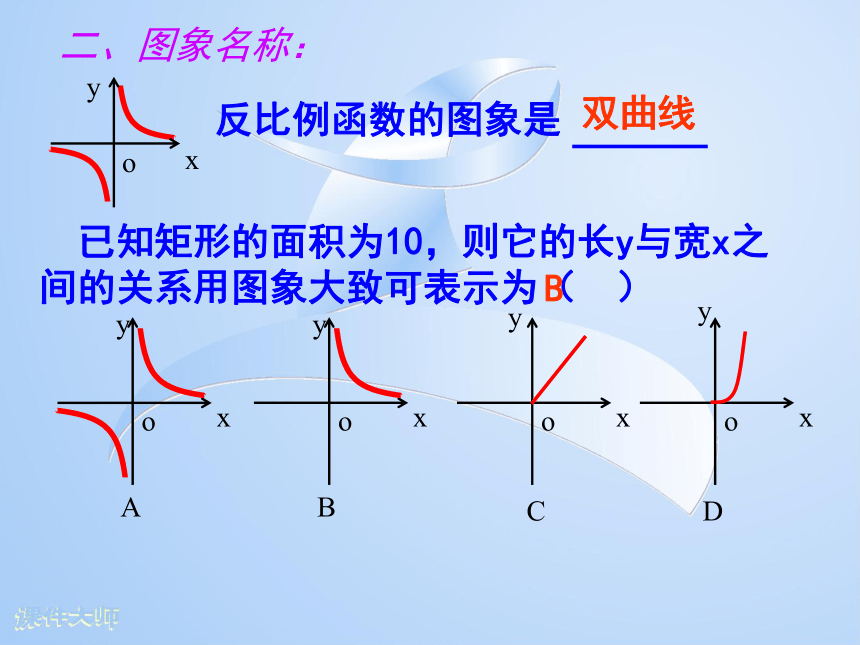
反比例函数。y=kx-1xy=ky与x成反比例等价形式：（k≠0）（k≠0）（k≠0） （k≠0,k为常数）y=-2x-1xy=－54y=x2、当k为 时，函数y=(k2+k) 是反比例函数？⑨①1、下列函数中y与x是反比例函数的有哪些?②③④⑤⑥⑦⑧2 3、近视眼镜的度数y(度)与镜片焦距x(米) 成反比例.已知400度近视眼镜的镜片焦距为0.25米,则y与x的函数关系是： 4、下表中分别给出了变量y与x之间的对应关 系，其中是反比例函数关系的是（ ）ABCDD5、若点(3,4)是反比例函数 图象上的一点，则此函数图象必经过点（ ） A(2,6) B(2,-6) C(4,-3) D(3,-4) A反比例函数的图象是二、图象名称： 已知矩形的面积为10，则它的长y与宽x之间的关系用图象大致可表示为（ ）AB双曲线B
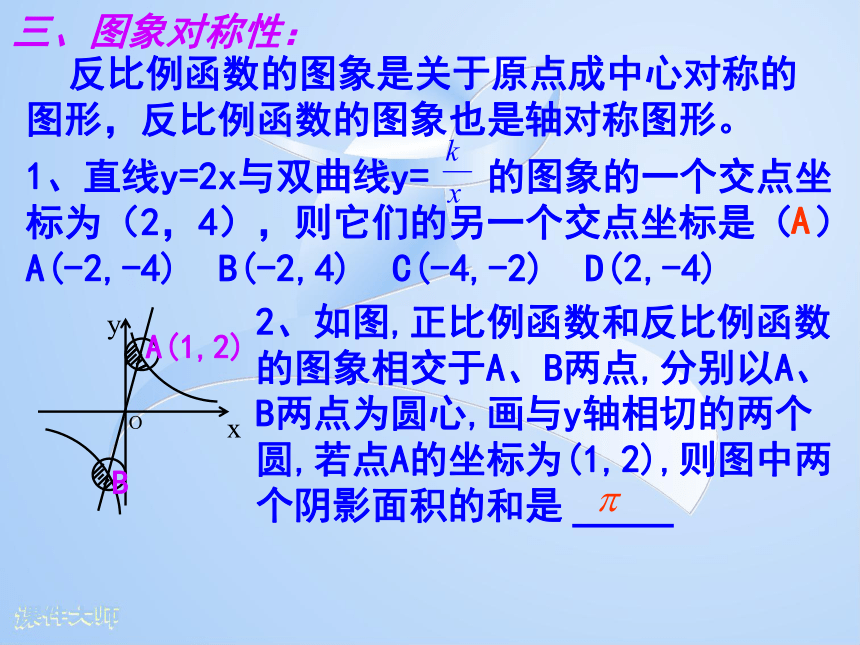
反比例函数的图象是关于原点成中心对称的图形，反比例函数的图象也是轴对称图形。三、图象对称性：2、如图,正比例函数和反比例函数的图象相交于A、B两点,分别以A、B两点为圆心,画与y轴相切的两个圆,若点A的坐标为(1,2),则图中两个阴影面积的和是1、直线y=2x与双曲线y= 的图象的一个交点坐标为（2，4），则它们的另一个交点坐标是（ ）
A(-2,-4) B(-2,4) C(-4,-2) D(2,-4)A 反比例函数的图象无限接近于x轴、y轴,但永远达不到x、y轴。四、图象渐近性：
当k>0时，图象分别在_____________，
当k<0时，图象分别在____________。五、图象位置:一、三象限二、四象限 已知反比例函数 ，其图象在第一、第三象限内，则k的值可以是 （写出满足条件的一个k的值即可）六、图象增减性：当k>0时，在每一象限内，y随x的增大而增大，
当k<0时，在每一象限内，y随x的增大而减小。..x4...y4y1 已知：在函数 （a为常数）的图象上
有三点 ,则函数y1、y2、y3 值
的大小关系是（ ）
A y2＜y3＜y1 B y3＜y2＜y1
C y1＜y3＜y2 D y3＜y1＜y2
D
S矩形=
1、A是双曲线y= 上一点，过点A向x轴作垂线,垂足为B，向y轴作垂线,垂足为C,则四边形OBAC的面积= 七、面积不变性:

S矩形= xy = k5ySRt△=2、如图，P1、P2、P3是双曲线上的三点，过这三点分别作y轴的垂线，得三个三角形△P1A1O、△P2A2O、△P3A3O,设它们的面积分别是S1 S2 S3，则( ) A s1< s2C s1=s2=s3 D S1 3、已知：A,B是函数y= 的图象上关于原点O对称的任意两点，AC//y轴，BC//x轴，ABC的面积S,则（ ）
A S=1 B 12△C4、如图是三个反比例函数
在x轴上方的图象，由此观察得到( )
A k1>k2>k3 B k3>k2>k1
C k2>k1>k3 D k3>k1>k2B5、如图,在直角坐标系中,直线y=6-x与函数y= (x>0)的图象相交于点A、B,设点A的坐标为(x1,y1),那么长为x1 、宽为y1的矩形面积和周长分别为（ ）A 4,12 B 8,12 C 4,6 D 8,6A1、如图:过双曲线 上任一点分别作x轴、y轴的垂线段，与x轴、y轴围成矩形面积为2，则此函数解析式为 2、已知：A是双曲线上的一点，过点A向x轴作垂线，垂足为B，△AOB的面积是4,则它的解析式为 解析式的求法：3、已知函数y=y1+y2，y1与x成正比例，y2与x成反比例，且当x=1时，y=-1;当x=3时，y=5，求y关于x的函数关系式。4、如图，一次函数的图象与x轴、y轴分别交于A、B两点，与反比例函数的图象交于C、D两点，A( ,0), OA=OB=AC.
（1）求一次函数的解析式
（2）求反比例函数的解析式
（3）求点D的坐标。小结：1、反比例函数的概念2、反比例函数的图象和性质3、反比例函数解析式的求法4、反比例函数的应用感谢各位专家的光临和指导！思考题： 如图，△P1OA1、△P2A1A2是等腰直角三角形，点P1、P2在函数 （x>0）的图象上，斜边OA1、A1A2都在x轴上，求点A2的坐标。