18.3.3一次函数的性质(3)[下学期]
文档属性
| 名称 | 18.3.3一次函数的性质(3)[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 23.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-12-14 13:49:00 | ||
图片预览




文档简介
课件10张PPT。17.3.3一次函数的性质(3)填空题
(1)若点A(-1,1)在函数y=kx的图象上,则k= 。
(2)一次函数y=3x-b过A(-2,1),则b= ,该图象经过点B( ,-1)和C(0, )。
(3)如图,直线l是y=kx+b的图象,看图填空。①k= ,b=
②当x=2时,y= ;
③当y=-2时,x= ;
④当x 时,y<0;
⑤y随x的增大而 .-3y(4)当m= 时,y=3x2m-4是正比例函数.
(5)已知一次函数y=mx+m+1,当m= 时,图象经过原点;当m= 时,图象经过(0,5).选择题
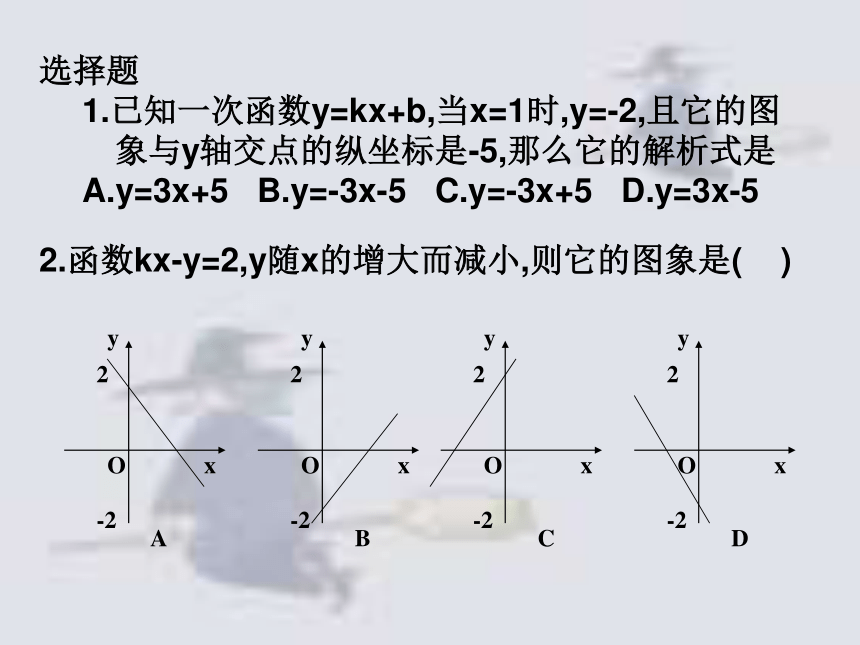
1.已知一次函数y=kx+b,当x=1时,y=-2,且它的图象与y轴交点的纵坐标是-5,那么它的解析式是
A.y=3x+5 B.y=-3x-5 C.y=-3x+5 D.y=3x-52.函数kx-y=2,y随x的增大而减小,则它的图象是( ) 例1.已知弹簧的长度g(厘米)在一定的限度内是所挂重物质量x(千克)的一次函数。现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的关系式。分析:已知y与x的函数关系式是一次函数,则关系式必是y=kx+b的形式,所以要求的就是系数k和b的值,而两个已知条件就是x和y的两组对应值,也就是当x=0时,y=6;当x=4时,y=7.2。可以分别将它们代入函数式,进而求得k和b的值。解:设所求的函数关系式是y=kx+b(k≠O),根据题意,得解这个方程组,得 所以所求函数关系式是y=0.3x+6, 其中x有一定范围。 例2.(2002佛山市题)某摩托车油箱最多可存油5升,行驶时油箱的余油量y(升)与行驶的路程x(千米)成一次函数的关系,其图象如图所示:
(1)求y与x的函数关系式;
(2)摩托车加满油后,最多能行驶多少千米 解:(1) 设y=kx+b(k≠0)当x=0时,y=5,∴ b=5.当x=60时,y=3,∴ 60k+5=3. ∴ k=-1/30(2) 把y=0代入函数关系式,得-1/30·x+5=0∴x=150故摩托车加满油后,最多能行驶150千米.例3.如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题
(1)当行使8千米时,收费应为 元
(2)从图象上你能获得哪些信息?(请写出2条)
①_________________________.
②__________________________.
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式11起步价为5元超过3千米,收费和行驶路程之间是一次函数的关系解: 当3≤x时,设y=kx+b(k≠0);由图象知, x=3时,y=5 ;x=8时,y=11,例4.某市移动通讯公司开设了两种通讯业务,"全球通"使用者先缴50元基础费,然后每通话1分钟,再付电话费0.4元;"神州行"不缴月基础费,每通话1分钟,付话费0.6元(这里均指市内通话).若一个月内通话x分钟,两种通讯方式的费用分别为y1元和y2元.
(1)出y1,y2与x之间的函数关系式;
(2)一个月内通话多少分钟,两种通讯方式的费用相同? 解:(1) 由已知得,y1=0.4x+50,y2=0.6x,(2) 设y1=y2,则0.4x+50=0.6x∴ x=250故,当一个月内通话250分钟,两种通讯方式的费用相同(3)如果是你,选择哪种通讯方式较省钱?例5.购买作业本每个0.5元,若数量不少于10本,则按9折优惠,
⑴写出应付金额y与购买数量x之间的函数关系式;
⑵求购买8本、55本的金额;
⑶画出上述函数的图象;
⑷若需9本作业本,怎样购买合算? 29.(2003省题)某人从A城出发,前往离A城30km的B城.现在有三种车供他选择:①自行车,其速度为15km/h;②三轮车,其速度为10km/h;③摩托车,其速度为40km/h.
(1)用哪种车能使他从A城到达B城的时间不超过2h,请说明理由.
(2)设此人在行进途中离B城的路程为skm,行进时间为th.就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围) (2002肇庆市题)在直角坐标系中,已知点A(1, )、B 、O(坐标原点)三点,试说明A、O、B三点在同一条直线上。
(1)若点A(-1,1)在函数y=kx的图象上,则k= 。
(2)一次函数y=3x-b过A(-2,1),则b= ,该图象经过点B( ,-1)和C(0, )。
(3)如图,直线l是y=kx+b的图象,看图填空。①k= ,b=
②当x=2时,y= ;
③当y=-2时,x= ;
④当x 时,y<0;
⑤y随x的增大而 .-3y(4)当m= 时,y=3x2m-4是正比例函数.
(5)已知一次函数y=mx+m+1,当m= 时,图象经过原点;当m= 时,图象经过(0,5).选择题
1.已知一次函数y=kx+b,当x=1时,y=-2,且它的图象与y轴交点的纵坐标是-5,那么它的解析式是
A.y=3x+5 B.y=-3x-5 C.y=-3x+5 D.y=3x-52.函数kx-y=2,y随x的增大而减小,则它的图象是( ) 例1.已知弹簧的长度g(厘米)在一定的限度内是所挂重物质量x(千克)的一次函数。现已测得不挂重物时弹簧的长度是6厘米,挂4千克质量的重物时,弹簧的长度是7.2厘米,求这个一次函数的关系式。分析:已知y与x的函数关系式是一次函数,则关系式必是y=kx+b的形式,所以要求的就是系数k和b的值,而两个已知条件就是x和y的两组对应值,也就是当x=0时,y=6;当x=4时,y=7.2。可以分别将它们代入函数式,进而求得k和b的值。解:设所求的函数关系式是y=kx+b(k≠O),根据题意,得解这个方程组,得 所以所求函数关系式是y=0.3x+6, 其中x有一定范围。 例2.(2002佛山市题)某摩托车油箱最多可存油5升,行驶时油箱的余油量y(升)与行驶的路程x(千米)成一次函数的关系,其图象如图所示:
(1)求y与x的函数关系式;
(2)摩托车加满油后,最多能行驶多少千米 解:(1) 设y=kx+b(k≠0)当x=0时,y=5,∴ b=5.当x=60时,y=3,∴ 60k+5=3. ∴ k=-1/30(2) 把y=0代入函数关系式,得-1/30·x+5=0∴x=150故摩托车加满油后,最多能行驶150千米.例3.如图是某出租车单程收费y(元)与行驶路程x(千米)之间的函数关系图象,根据图象回答下列问题
(1)当行使8千米时,收费应为 元
(2)从图象上你能获得哪些信息?(请写出2条)
①_________________________.
②__________________________.
(3)求出收费y(元)与行使x(千米)(x≥3)之间的函数关系式11起步价为5元超过3千米,收费和行驶路程之间是一次函数的关系解: 当3≤x时,设y=kx+b(k≠0);由图象知, x=3时,y=5 ;x=8时,y=11,例4.某市移动通讯公司开设了两种通讯业务,"全球通"使用者先缴50元基础费,然后每通话1分钟,再付电话费0.4元;"神州行"不缴月基础费,每通话1分钟,付话费0.6元(这里均指市内通话).若一个月内通话x分钟,两种通讯方式的费用分别为y1元和y2元.
(1)出y1,y2与x之间的函数关系式;
(2)一个月内通话多少分钟,两种通讯方式的费用相同? 解:(1) 由已知得,y1=0.4x+50,y2=0.6x,(2) 设y1=y2,则0.4x+50=0.6x∴ x=250故,当一个月内通话250分钟,两种通讯方式的费用相同(3)如果是你,选择哪种通讯方式较省钱?例5.购买作业本每个0.5元,若数量不少于10本,则按9折优惠,
⑴写出应付金额y与购买数量x之间的函数关系式;
⑵求购买8本、55本的金额;
⑶画出上述函数的图象;
⑷若需9本作业本,怎样购买合算? 29.(2003省题)某人从A城出发,前往离A城30km的B城.现在有三种车供他选择:①自行车,其速度为15km/h;②三轮车,其速度为10km/h;③摩托车,其速度为40km/h.
(1)用哪种车能使他从A城到达B城的时间不超过2h,请说明理由.
(2)设此人在行进途中离B城的路程为skm,行进时间为th.就(1)所选定的方案,试写出s与t的函数关系式(注明自变量t的取值范围) (2002肇庆市题)在直角坐标系中,已知点A(1, )、B 、O(坐标原点)三点,试说明A、O、B三点在同一条直线上。
