18.3 一次函数的图象(1)[下学期]
文档属性
| 名称 | 18.3 一次函数的图象(1)[下学期] |

|
|
| 格式 | rar | ||
| 文件大小 | 374.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-11-03 08:03:00 | ||
图片预览





文档简介
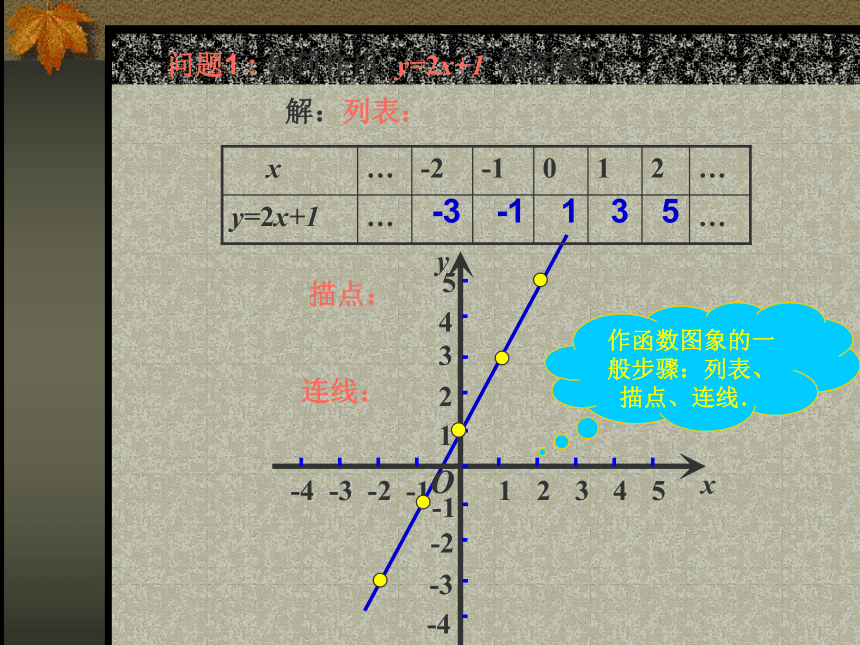
课件22张PPT。§17.3.2一次函数的图象复习回顾:1.什么是一次函数?它的一般表达式是怎样?2.什么是正比例函数?它的一般表达式是怎样的?3.绘制函数图象,你学过什么方法?描 点 法问题1 : 如何作出 y=2x+1 的图象?连线:-3-1153作函数图象的一般步骤:列表、描点、连线.结合图象回答下列问题
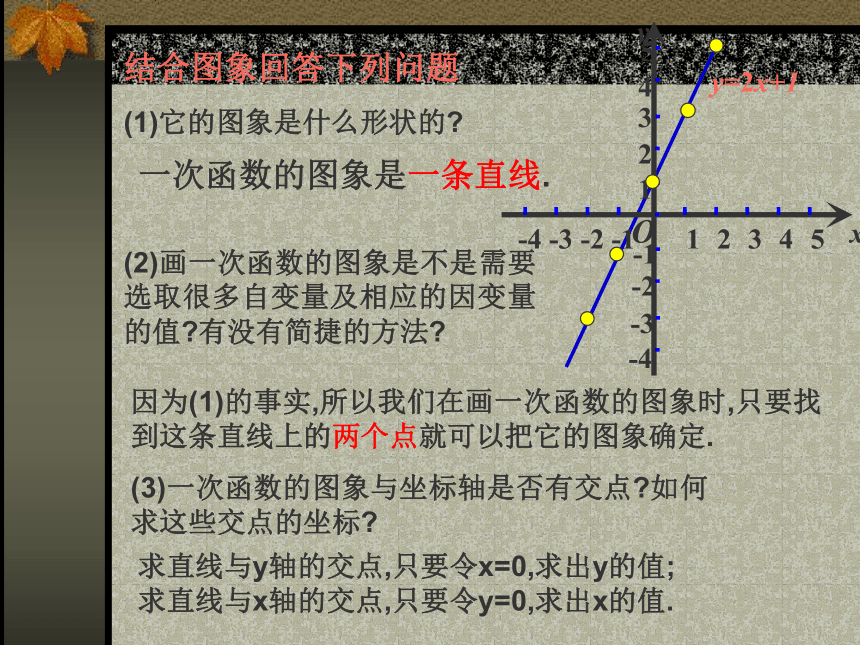
(1)它的图象是什么形状的?一次函数的图象是一条直线.(2)画一次函数的图象是不是需要选取很多自变量及相应的因变量的值?有没有简捷的方法?因为(1)的事实,所以我们在画一次函数的图象时,只要找到这条直线上的两个点就可以把它的图象确定.(3)一次函数的图象与坐标轴是否有交点?如何求这些交点的坐标?求直线与y轴的交点,只要令x=0,求出y的值;
求直线与x轴的交点,只要令y=0,求出x的值.例1:求直线y=-2x-4与x轴和y轴的交点,并
画出图象.解:令x=0,则y=-2×0-4=-4.
即直线与y轴的交点坐标为(0,-4). 令y=0,则0=-2x-4.所以x=-2
即直线与x轴的交点坐标为(-2,0).思考:
(1)正比例函数的图象是怎样的?
(2)绘制正比例函数图象如何画
最简单?一次函数的图象与Y轴的交点坐标为(0,b)y=-2x-4例2:试画出函数y=-2x图象.正比例函数的图象是经过原点的一条直线!想一想:
正比例函数的图象必定
过哪个点?必定过原点!y=-2x问题2:在同一个平面直角坐标系中画出下列
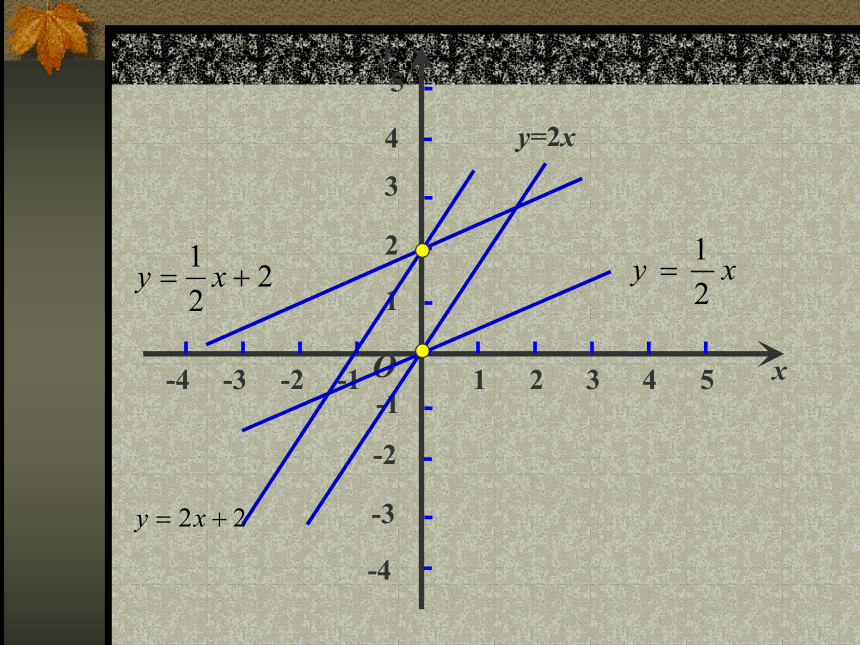
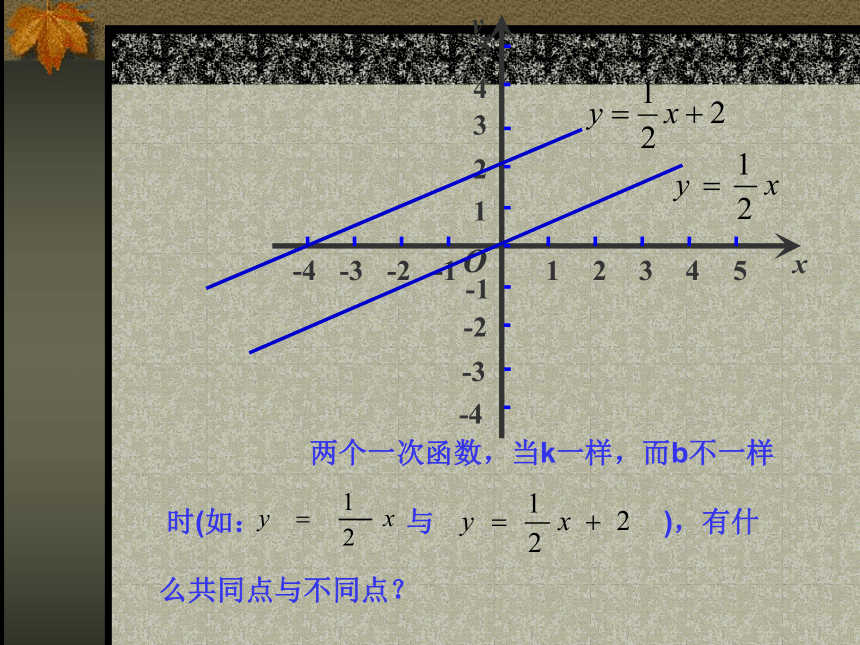
函数的图象:y=2x 两个一次函数,当k一样,而b不一样
时(如: 与 ),有什
么共同点与不同点?
共同点:两者的图形都是直线,且互相平行;是由上面的直线向下平移2个单位长度得到的。
不同点: 经过原点(0,0),
而 与y轴交于点(0,2),
与x轴交于点(-4,0)
我们再来看函数 与 ,则它们又有何异同点呢?(它们的b一样,而k不一样)1.共同点:两者的图形都是直线,且
均过点(0,2)。即(0,b)2.不同点: 与x轴交于
点 (-1,0), 而 与x轴交
于点(-4,0)。?归纳:(对y=kx+b而言)1、当两个一次函数的k一样,而b不一 样,则这两个函数的图象是两条互相平行的直线,且它们之间可以通过平移得到(向上或向下)。
2、当两个一次函数的b一样,而k不一样,则这两个函数的图象是两条相交的直线,且与y轴交于同一点,即(0,b)
y=2x1.将直线y=-3x+1向下平移5个单位后得到直线_______
2.将直线y=2x向上平移____个单位得到一次函 数y=2x+2的图象.
3.将直线y=-x+b向上平移2个单位得到直线
y=-x+1,则b=_______.
4.若直线y=-x-5与直线y=x- b相交于y轴上同一点,则b=_______.y=-3x-42-154332211O-1-1-2-2-3-3-4-4分析:(0, )( ,0)?4?AB三角形AOB的面积=y=2x+44-2xy24已知一次函数y=2x+4,求其与两坐标轴所围成的三角形的面积?练一练1.教材P.42 例题
2.练习1、21.直线y=x-3与y=3x+b都经过y轴上的同一点,则b=_____.
2.要从直线 得到 的图象,
那么必须将直线 向___平移____个单位.
3.经过点(0,-2),且与直线 平行的直线是_________.-3上4.拖拉机开始工作时,油箱中有油24L,若每小时耗油4L,那么油箱中剩余油量y(L)与工作时间x(h)之间的函数关系式和图象是( ) A. y=4x-24(0≤x≤6) B. y=24-4x
C. y=24-4x (0≤x ≤6 ) D. y=-24+4x ?
DC5. 如图,l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;20003000(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;60005000(3)当销售量为 时,销售收入等于销售成本;4吨小结1. y=kx+b(k≠0)的图象是一条直线,画图时只需取两点.
y=kx(k≠0)的图象是经过原点的直线,画图时只需取
点(1,k)2. 在y=kx+b(k≠0)中,当k的值相同时,几条直线互相平行.3.在y=kx+b(k≠0)中,b的值确定直线与y轴交点的位置,即图象经过(0,b).
当b>0时,交点在x轴的上方;
当b<0时,交点在x轴的下方;
当b=0时,图象经过原点.再见
(1)它的图象是什么形状的?一次函数的图象是一条直线.(2)画一次函数的图象是不是需要选取很多自变量及相应的因变量的值?有没有简捷的方法?因为(1)的事实,所以我们在画一次函数的图象时,只要找到这条直线上的两个点就可以把它的图象确定.(3)一次函数的图象与坐标轴是否有交点?如何求这些交点的坐标?求直线与y轴的交点,只要令x=0,求出y的值;
求直线与x轴的交点,只要令y=0,求出x的值.例1:求直线y=-2x-4与x轴和y轴的交点,并
画出图象.解:令x=0,则y=-2×0-4=-4.
即直线与y轴的交点坐标为(0,-4). 令y=0,则0=-2x-4.所以x=-2
即直线与x轴的交点坐标为(-2,0).思考:
(1)正比例函数的图象是怎样的?
(2)绘制正比例函数图象如何画
最简单?一次函数的图象与Y轴的交点坐标为(0,b)y=-2x-4例2:试画出函数y=-2x图象.正比例函数的图象是经过原点的一条直线!想一想:
正比例函数的图象必定
过哪个点?必定过原点!y=-2x问题2:在同一个平面直角坐标系中画出下列
函数的图象:y=2x 两个一次函数,当k一样,而b不一样
时(如: 与 ),有什
么共同点与不同点?
共同点:两者的图形都是直线,且互相平行;是由上面的直线向下平移2个单位长度得到的。
不同点: 经过原点(0,0),
而 与y轴交于点(0,2),
与x轴交于点(-4,0)
我们再来看函数 与 ,则它们又有何异同点呢?(它们的b一样,而k不一样)1.共同点:两者的图形都是直线,且
均过点(0,2)。即(0,b)2.不同点: 与x轴交于
点 (-1,0), 而 与x轴交
于点(-4,0)。?归纳:(对y=kx+b而言)1、当两个一次函数的k一样,而b不一 样,则这两个函数的图象是两条互相平行的直线,且它们之间可以通过平移得到(向上或向下)。
2、当两个一次函数的b一样,而k不一样,则这两个函数的图象是两条相交的直线,且与y轴交于同一点,即(0,b)
y=2x1.将直线y=-3x+1向下平移5个单位后得到直线_______
2.将直线y=2x向上平移____个单位得到一次函 数y=2x+2的图象.
3.将直线y=-x+b向上平移2个单位得到直线
y=-x+1,则b=_______.
4.若直线y=-x-5与直线y=x- b相交于y轴上同一点,则b=_______.y=-3x-42-154332211O-1-1-2-2-3-3-4-4分析:(0, )( ,0)?4?AB三角形AOB的面积=y=2x+44-2xy24已知一次函数y=2x+4,求其与两坐标轴所围成的三角形的面积?练一练1.教材P.42 例题
2.练习1、21.直线y=x-3与y=3x+b都经过y轴上的同一点,则b=_____.
2.要从直线 得到 的图象,
那么必须将直线 向___平移____个单位.
3.经过点(0,-2),且与直线 平行的直线是_________.-3上4.拖拉机开始工作时,油箱中有油24L,若每小时耗油4L,那么油箱中剩余油量y(L)与工作时间x(h)之间的函数关系式和图象是( ) A. y=4x-24(0≤x≤6) B. y=24-4x
C. y=24-4x (0≤x ≤6 ) D. y=-24+4x ?
DC5. 如图,l1反映了某公司产品的销售收入与销售量的关系,l2反映了该公司产品的销售成本与销售量的关系,根据图意填空:(1)当销售量为2吨时,销售收入= 元,
销售成本= 元;20003000(2)当销售量为6吨时,销售收入= 元,
销售成本= 元;60005000(3)当销售量为 时,销售收入等于销售成本;4吨小结1. y=kx+b(k≠0)的图象是一条直线,画图时只需取两点.
y=kx(k≠0)的图象是经过原点的直线,画图时只需取
点(1,k)2. 在y=kx+b(k≠0)中,当k的值相同时,几条直线互相平行.3.在y=kx+b(k≠0)中,b的值确定直线与y轴交点的位置,即图象经过(0,b).
当b>0时,交点在x轴的上方;
当b<0时,交点在x轴的下方;
当b=0时,图象经过原点.再见
