浙教版科学中考复习专题训练:滑轮组相关计算【word,含答案】
文档属性
| 名称 | 浙教版科学中考复习专题训练:滑轮组相关计算【word,含答案】 |  | |
| 格式 | docx | ||
| 文件大小 | 110.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 科学 | ||
| 更新时间 | 2023-03-15 08:17:12 | ||
图片预览



文档简介
滑轮组相关计算
1. 如图,塔式起重机上的滑轮组将重为1.2×104 N的重物匀速吊起2 m时,滑轮组的机械效率为80%,g取10 N/kg.
(1)求提升重物做的有用功;
(2)求绳端的拉力;
(3)若动滑轮的质量为40 kg,求克服摩擦和钢绳重所做的功.
第1题图
2. 一辆质量为1.5×103 kg的汽车陷入一泥泞路段,司机师傅利用滑轮组和周围条件,组装成了如图所示的拖车装置.已知汽车通过泥泞路段需移动8 m距离,汽车在泥泞路段受到的阻力为车重的0.1 倍,滑轮组的机械效率为80%,g取10 N/kg.在将车匀速拖离泥泞路段过程中,求:
(1)做的有用功;
(2)作用在绳子自由端的拉力.
第2题图
3. 如图所示,某建筑工地用起重机将质量为3.6 t的货箱以0.5 m/s的速度匀速提升,吊臂上的滑轮组如图所示,若忽略绳重和摩擦,该滑轮组的机械效率为80%.(g取10 N/kg)求:
(1)在10 s内货箱上升的高度;
(2)货箱的重力;
(3)吊臂上电动机拉力F的大小;
(4)依然利用此机械提升质量为4.1 t的货箱,求此时滑轮组的机械效率.
第3题图
4. 在九年级物理拓展课上,李博同学模拟某建筑工地上塔吊的工作情景,设置了如图所示的滑轮组来提升装修材料,若他用250 N的拉力在20 s内将450 N的材料提升了10 m,(不计绳重和摩擦,g取10 N/kg).求:
(1)拉力的功率是多少?
(2)提升450 N材料时,此滑轮组的机械效率是多少?
(3)若绳子能承受的最大拉力为400 N时,此滑轮组的机械效率最大可提高到多少?
第4题图
5. 小雨同学家装修新房,看到工人师傅使用如图所示的一种自制的简易起重装置向楼上吊装笨重的装修材料,感觉该装置简单易制、方便快捷,大大减少了工人搬运材料的劳动强度.小雨观察到电动机的输出功率800 W,将两袋(每袋质量50 kg)水泥匀速提升到10 m高的4楼需要用时15 s.假设电动机的输出功率恒定不变.请帮小雨完成下列问题: (g取10 N/kg)
第5题图
(1)此次吊装过程中绳子自由端移动的速度是多大?
(2)电动机对绳子的拉力多大?
(3)该滑轮组的机械效率多大?
6. 如图所示,在科普节目《加油,向未来》中,有一项对抗性实验,甲、乙两人站在平衡板上,滑轮组将平衡板提升至一定高度后 ,两人在平衡板上挪动,并保持平衡板平衡.若甲的质量为55 kg,乙的质量为45 kg.平衡板质量为900 kg,且质量分布均匀,重心在点O.(g取10 N/kg)
(1)当平衡板在水平地面上时,甲静止站在平衡板上,与板的接触面积为0.05 m2,则甲对平衡板的压强为多大?
(2)甲、乙两人竖直站在平衡板上,滑轮组将平衡板匀速提升至离地面5 m的高度处,提升的过程中平衡板始终保持水平平衡,拉力F为6 250 N,求在此过程中:
①平衡板提升两人所做的功为多少?
②在提升平衡板和人的过程中,滑轮组的机械效率为多少?
(3)当甲、乙两人竖直站立在图中A、B位置时,平衡板在空中处于水平平衡,甲、乙两人从图中位置同时向平衡板左、右两侧沿同一直线向相反方向缓慢挪动至C、D竖直站立时,平衡板也恰好处于水平平衡,则两人挪动的距离AC和BD之比为________.
第6题图
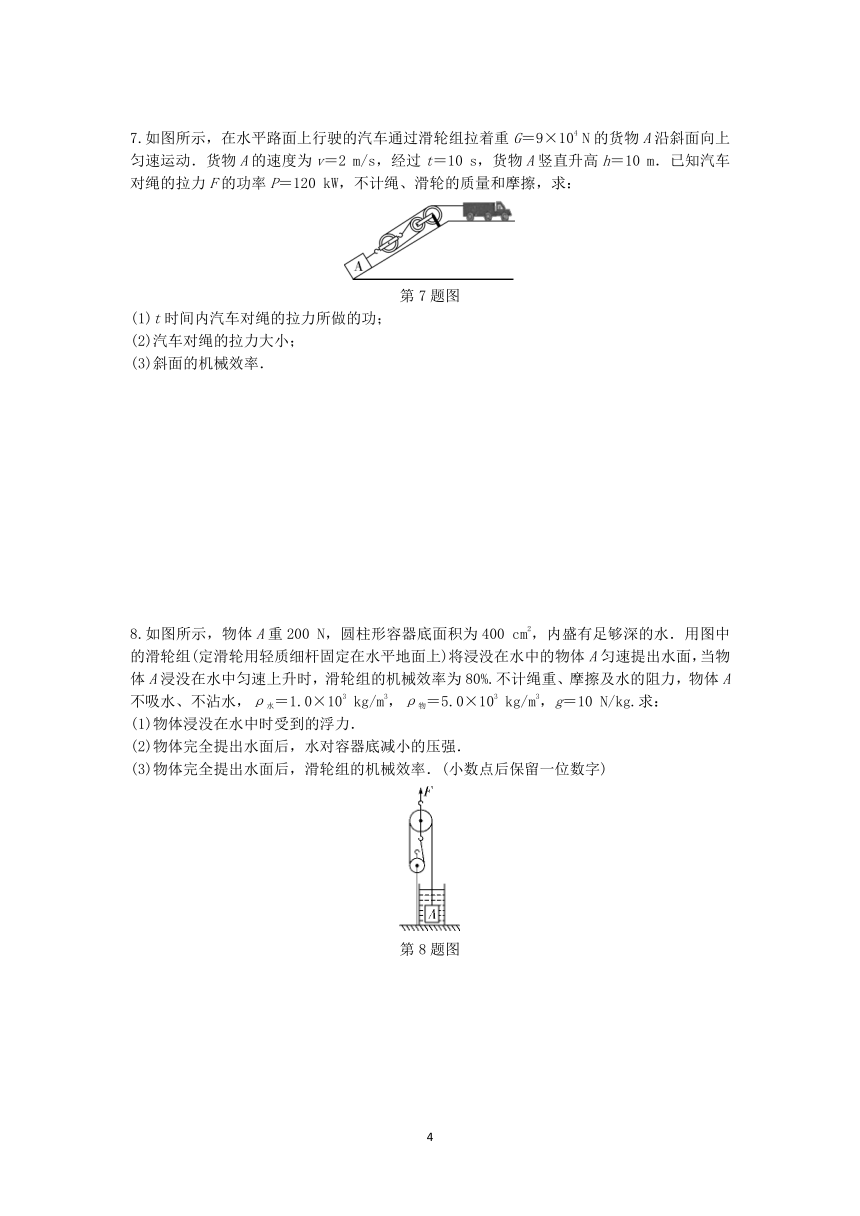
7.如图所示,在水平路面上行驶的汽车通过滑轮组拉着重G=9×104 N的货物A沿斜面向上匀速运动.货物A的速度为v=2 m/s,经过t=10 s,货物A竖直升高h=10 m.已知汽车对绳的拉力F的功率P=120 kW,不计绳、滑轮的质量和摩擦,求:
第7题图
(1)t时间内汽车对绳的拉力所做的功;
(2)汽车对绳的拉力大小;
(3)斜面的机械效率.
8.如图所示,物体A重200 N,圆柱形容器底面积为400 cm2,内盛有足够深的水.用图中的滑轮组(定滑轮用轻质细杆固定在水平地面上)将浸没在水中的物体A匀速提出水面,当物体A浸没在水中匀速上升时,滑轮组的机械效率为80%.不计绳重、摩擦及水的阻力,物体A不吸水、不沾水,ρ水=1.0×103 kg/m3,ρ物=5.0×103 kg/m3,g=10 N/kg.求:
(1)物体浸没在水中时受到的浮力.
(2)物体完全提出水面后,水对容器底减小的压强.
(3)物体完全提出水面后,滑轮组的机械效率.(小数点后保留一位数字)
第8题图
9.图甲是工人使用滑轮组打捞不慎落入水中的圆柱形石料M的示意图.在整个打捞过程中,石料以恒定的速度v=0.1 m/s上升,石料离开水面之后绳子自由端的拉力F=2 000 N.图乙是钢丝绳的拉力T随时间t变化的图像,t=0时刻石料刚好离开河底.g取10 N/kg,水的密度ρ=1.0×103 kg/m3.
(1)画出图甲中石料M离开水面后的受力示意图.
(2)石料完全浸没在水中受到的浮力是________N,石料质量是________kg.
(3)河底受到水的压强是多少?
(4)石料离开水面之后滑轮组的机械效率是多少?
第9题图
10.如图所示,一个质量600 kg、体积0.2 m3的箱子沉入5 m深的水底,水面距离地面2 m,若利用滑轮组和电动机组成的打捞机械,以0.5 m/s的速度将箱子从水底匀速提到地面,每个滑轮重100 N(不计绳重、摩擦和水的阻力,ρ水=1.0×103 kg/m3,g=10 N/kg).求:
(1)箱子在水底时,箱子下表面受到的水的压强;
(2)箱子全部浸没在水中时,箱子受到的浮力;
(3)物体完全露出水面后,继续上升到地面的过程中,滑轮组的机械效率;
(4)整个打捞过程中,请你分析哪个阶段电动机的输出功率最大,并计算出这个最大值.
参考答案
1. 解:(1)提升重物做的有用功
W有=Gh=1.2×104 N×2 m=2.4×104 J
(2)由η=×100%可得
W总===3.0×104 J
由图可知,n=3
故绳端移动的距离
s=nh=3×2 m=6 m
绳端的拉力F===5×103 N
(3)由题可知,动滑轮重
G′=mg=40 kg×10 N/kg=400 N
克服动滑轮重力所做的功
W动=G′h=400 N×2 m=800 J
W额=W总-W有=3.0×104 J-2.4×104 J=6×103 J
克服摩擦和钢绳重所做的功W摩擦=W额-W动=6×103 J-0.8×103 J=5.2×103 J
2. 解:(1)汽车所受的阻力
f=0.1mg=0.1×1.5×103 kg×10 N/kg=1.5×103 N
将车匀速拖离,由二力平衡得,牵引力F牵=f=1.5×103 N
所做的有用功
W有=F牵s车=1.5×103 N×8 m=1.2×104 J
(2)由图可知,n=3,故绳子自由端移动距离s绳=3s车=3×8 m=24 m
由η=×100%得,W总===1.5×104 J
由W总=Fs绳得,拉力F===625 N
3. 解:(1)10 s内货箱上升的高度h=v货t=0.5 m/s×10 s=5 m
(2)货箱的重力G货=mg=3.6×103 kg×10 N/kg=3.6×104 N
(3)由η=×100%=×100%=×100%=×100%得,
拉力F的大小为F===1.5×104 N
(4)由于物体的总重由3段绳子承担,所以有3F=G+G动
动滑轮的重力G动=3F-G=3×1.5×104 N-3.6×104 N=9×103 N
当提升质量为4.1 t货箱时,滑轮组的机械效率为
η′=×100%=×100%=×100%=×100%=×100%=82%
4. 解:(1)由图可知,n=3,则绳端移动的距离为
s=nh=3×10 m=30 m
拉力做的功为W=Fs=250 N×30 m=7 500 J,拉力的功率为P===375 W
(2)机械效率为η=×100%=×100%=×100%=×100%=60%
(3)由F=(G+G动)得
动滑轮重力为G动=nF-G=3×250 N-450 N=300 N
能吊起物体的最大重力为G′=nF′-G动=3×400 N-300 N=900 N
滑轮组最大机械效率为η′=×100%=×100%=75%
5. 解:(1)由图可知,承担动滑轮绳子的段数为n=3
水泥运动的速度为v水泥=== m/s
绳子自由端移动的速度v绳=3v水泥=3×m/s=2 m/s
(2)由P===Fv得,电动机对绳子的拉力
F===400 N
(3)有用功为W有用=G水泥h=m水泥gh=2×50 kg×10 N/kg×10 m=1×104 J
电动机做的总功W总=Pt=800 W×15 s=1.2×104 J
滑轮组的机械效率η=×100%=×100%≈83.33%
6. 解:(1)甲对平衡板的压力F甲=G甲=m甲g=55 kg×10 N/kg=550 N,与板的接触面积S=0.05 m2
甲对平衡板的压强p===1.1×104 Pa
(2)提升过程中,平衡板对甲、乙两人的支持力:
F′=G甲+G乙=(m甲+m乙)g=(55 kg+45 kg)×10 N/kg=1 000 N
平衡板将两人提升的高度:h=5 m
①平衡板提升两人所做的功W=F′h=1000 N×5 m=5 000 J
②由图可知,n=2,则拉力所做的总功W总=Fs=2Fh=2×6 250 N×5 m=6.25×104 J
滑轮组做的有用功W有=(G甲+G乙+G板)h=(55 kg+45 kg+900 kg)×10 N/kg×5 m=5×104 J
滑轮组的机械效率η=×100%=×100%=80%
(3)9∶11 【解析】根据杠杆的平衡条件
G甲×OA=G乙×OB
移动后重新平衡时
G甲×(OA+AC)=G乙×(OB+BD)
G甲×OA+G甲×AC=G乙×OB+G乙×BD
G甲×AC=G乙×BD
550 N×AC=450 N×BD
AC∶BD=9∶11
7. 解:(1)已知汽车对绳的拉力F的功率P =120 kW,则t=10 s时间内汽车对绳的拉力做功:
W=Pt=1.2×105 W×10 s=1.2×106 J
(2)汽车拉着货物A沿斜面匀速行驶,速度一定,由题图知,n=3,由P=Fv得汽车对绳的拉力:F====2×104 N
(3)斜面的机械效率为:η=×100%=×100%=×100%=75%
8. 解:(1)物体的体积
V物====4×10-3 m3
则物体浸没在水中时受到的浮力
F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×4×10-3 m3=40 N
(2)物体完全提出水面后,水对容器底减小的压力
ΔF压=F浮=40 N
则物体完全提出水面后,水对容器底减小的压强
Δp压===1 000 Pa
(3)物体浸没在水中匀速上升时,滑轮组的机械效率
η1=×100%
即80%=
解得F=(G物-F浮)=×(200 N-40 N)=600 N
又因为F=3(G物-F浮)+G动
所以G动=F-3(G物-F浮)=600 N-3×(200 N-40 N)=120 N
则物体完全提出水面后,滑轮组的机械效率
η2=×100%=×100%≈83.3%
9. (1)如答图所示
第9题答图
(2)800 320
【解析】(2)由图乙可知,石料完全浸没在水里时所受浮力F浮=3 200 N-2 400 N=800 N;离开水面后绳子拉力T=G石料,所以石料质量m====320 kg.
解:(3)由图乙可知石料从开始运动到完全离开水面用时50 s,则河水的深度h=vt=0.1 m/s×50 s=5 m.根据液体压强公式得:河底受到水的压强p=ρgh=1×103 kg/m3×10 N/kg×5 m=5×104 Pa
(4)石料离开水后,绳子自由端拉力为2 000 N,滑轮组有一个动滑轮,两股绳子承重即n=2,由图乙可知,石料离开水后绳子的拉力T=G=3 200 N,离开水面后滑轮组的机械效率η=×100%=×100%=×100%=×100%=×100%=80%
10. 解:(1)箱子在水底时,下表面的深度为h=5 m,此时箱子下表面受到水的压强:p=ρ水gh=1.0×103 kg/m3×10 N/kg×5 m=5×104 Pa
(2)箱子受到的浮力:F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×0.2 m3=2×103 N
(3)物体完全露出水面后,已不受浮力,整套装置克服箱子重力做的功是有用功:
W有=G箱h′=m箱gh′=600 kg×10 N/kg×2 m=1.2×104 J
绳子自由端的拉力:F====3 050 N
则拉力所做的总功:
W总=Fs=F·2h=3 050 N×2×2 m=1.22×104 J
则此时滑轮组的机械效率:
η=×100%=×100%≈98%
(4)整个过程中,箱子的运动速度不变,根据P=Fv可知,绳端拉力F最大时,电动机的输出功率最大.当箱子离开水面时,箱子不受浮力作用,此时拉力F最大,F=3 050 N,最大功率为P=Fv绳 =F·2v箱=3 050 N×2×0.5 m/s=3 050 W
(
1
)
1. 如图,塔式起重机上的滑轮组将重为1.2×104 N的重物匀速吊起2 m时,滑轮组的机械效率为80%,g取10 N/kg.
(1)求提升重物做的有用功;
(2)求绳端的拉力;
(3)若动滑轮的质量为40 kg,求克服摩擦和钢绳重所做的功.
第1题图
2. 一辆质量为1.5×103 kg的汽车陷入一泥泞路段,司机师傅利用滑轮组和周围条件,组装成了如图所示的拖车装置.已知汽车通过泥泞路段需移动8 m距离,汽车在泥泞路段受到的阻力为车重的0.1 倍,滑轮组的机械效率为80%,g取10 N/kg.在将车匀速拖离泥泞路段过程中,求:
(1)做的有用功;
(2)作用在绳子自由端的拉力.
第2题图
3. 如图所示,某建筑工地用起重机将质量为3.6 t的货箱以0.5 m/s的速度匀速提升,吊臂上的滑轮组如图所示,若忽略绳重和摩擦,该滑轮组的机械效率为80%.(g取10 N/kg)求:
(1)在10 s内货箱上升的高度;
(2)货箱的重力;
(3)吊臂上电动机拉力F的大小;
(4)依然利用此机械提升质量为4.1 t的货箱,求此时滑轮组的机械效率.
第3题图
4. 在九年级物理拓展课上,李博同学模拟某建筑工地上塔吊的工作情景,设置了如图所示的滑轮组来提升装修材料,若他用250 N的拉力在20 s内将450 N的材料提升了10 m,(不计绳重和摩擦,g取10 N/kg).求:
(1)拉力的功率是多少?
(2)提升450 N材料时,此滑轮组的机械效率是多少?
(3)若绳子能承受的最大拉力为400 N时,此滑轮组的机械效率最大可提高到多少?
第4题图
5. 小雨同学家装修新房,看到工人师傅使用如图所示的一种自制的简易起重装置向楼上吊装笨重的装修材料,感觉该装置简单易制、方便快捷,大大减少了工人搬运材料的劳动强度.小雨观察到电动机的输出功率800 W,将两袋(每袋质量50 kg)水泥匀速提升到10 m高的4楼需要用时15 s.假设电动机的输出功率恒定不变.请帮小雨完成下列问题: (g取10 N/kg)
第5题图
(1)此次吊装过程中绳子自由端移动的速度是多大?
(2)电动机对绳子的拉力多大?
(3)该滑轮组的机械效率多大?
6. 如图所示,在科普节目《加油,向未来》中,有一项对抗性实验,甲、乙两人站在平衡板上,滑轮组将平衡板提升至一定高度后 ,两人在平衡板上挪动,并保持平衡板平衡.若甲的质量为55 kg,乙的质量为45 kg.平衡板质量为900 kg,且质量分布均匀,重心在点O.(g取10 N/kg)
(1)当平衡板在水平地面上时,甲静止站在平衡板上,与板的接触面积为0.05 m2,则甲对平衡板的压强为多大?
(2)甲、乙两人竖直站在平衡板上,滑轮组将平衡板匀速提升至离地面5 m的高度处,提升的过程中平衡板始终保持水平平衡,拉力F为6 250 N,求在此过程中:
①平衡板提升两人所做的功为多少?
②在提升平衡板和人的过程中,滑轮组的机械效率为多少?
(3)当甲、乙两人竖直站立在图中A、B位置时,平衡板在空中处于水平平衡,甲、乙两人从图中位置同时向平衡板左、右两侧沿同一直线向相反方向缓慢挪动至C、D竖直站立时,平衡板也恰好处于水平平衡,则两人挪动的距离AC和BD之比为________.
第6题图
7.如图所示,在水平路面上行驶的汽车通过滑轮组拉着重G=9×104 N的货物A沿斜面向上匀速运动.货物A的速度为v=2 m/s,经过t=10 s,货物A竖直升高h=10 m.已知汽车对绳的拉力F的功率P=120 kW,不计绳、滑轮的质量和摩擦,求:
第7题图
(1)t时间内汽车对绳的拉力所做的功;
(2)汽车对绳的拉力大小;
(3)斜面的机械效率.
8.如图所示,物体A重200 N,圆柱形容器底面积为400 cm2,内盛有足够深的水.用图中的滑轮组(定滑轮用轻质细杆固定在水平地面上)将浸没在水中的物体A匀速提出水面,当物体A浸没在水中匀速上升时,滑轮组的机械效率为80%.不计绳重、摩擦及水的阻力,物体A不吸水、不沾水,ρ水=1.0×103 kg/m3,ρ物=5.0×103 kg/m3,g=10 N/kg.求:
(1)物体浸没在水中时受到的浮力.
(2)物体完全提出水面后,水对容器底减小的压强.
(3)物体完全提出水面后,滑轮组的机械效率.(小数点后保留一位数字)
第8题图
9.图甲是工人使用滑轮组打捞不慎落入水中的圆柱形石料M的示意图.在整个打捞过程中,石料以恒定的速度v=0.1 m/s上升,石料离开水面之后绳子自由端的拉力F=2 000 N.图乙是钢丝绳的拉力T随时间t变化的图像,t=0时刻石料刚好离开河底.g取10 N/kg,水的密度ρ=1.0×103 kg/m3.
(1)画出图甲中石料M离开水面后的受力示意图.
(2)石料完全浸没在水中受到的浮力是________N,石料质量是________kg.
(3)河底受到水的压强是多少?
(4)石料离开水面之后滑轮组的机械效率是多少?
第9题图
10.如图所示,一个质量600 kg、体积0.2 m3的箱子沉入5 m深的水底,水面距离地面2 m,若利用滑轮组和电动机组成的打捞机械,以0.5 m/s的速度将箱子从水底匀速提到地面,每个滑轮重100 N(不计绳重、摩擦和水的阻力,ρ水=1.0×103 kg/m3,g=10 N/kg).求:
(1)箱子在水底时,箱子下表面受到的水的压强;
(2)箱子全部浸没在水中时,箱子受到的浮力;
(3)物体完全露出水面后,继续上升到地面的过程中,滑轮组的机械效率;
(4)整个打捞过程中,请你分析哪个阶段电动机的输出功率最大,并计算出这个最大值.
参考答案
1. 解:(1)提升重物做的有用功
W有=Gh=1.2×104 N×2 m=2.4×104 J
(2)由η=×100%可得
W总===3.0×104 J
由图可知,n=3
故绳端移动的距离
s=nh=3×2 m=6 m
绳端的拉力F===5×103 N
(3)由题可知,动滑轮重
G′=mg=40 kg×10 N/kg=400 N
克服动滑轮重力所做的功
W动=G′h=400 N×2 m=800 J
W额=W总-W有=3.0×104 J-2.4×104 J=6×103 J
克服摩擦和钢绳重所做的功W摩擦=W额-W动=6×103 J-0.8×103 J=5.2×103 J
2. 解:(1)汽车所受的阻力
f=0.1mg=0.1×1.5×103 kg×10 N/kg=1.5×103 N
将车匀速拖离,由二力平衡得,牵引力F牵=f=1.5×103 N
所做的有用功
W有=F牵s车=1.5×103 N×8 m=1.2×104 J
(2)由图可知,n=3,故绳子自由端移动距离s绳=3s车=3×8 m=24 m
由η=×100%得,W总===1.5×104 J
由W总=Fs绳得,拉力F===625 N
3. 解:(1)10 s内货箱上升的高度h=v货t=0.5 m/s×10 s=5 m
(2)货箱的重力G货=mg=3.6×103 kg×10 N/kg=3.6×104 N
(3)由η=×100%=×100%=×100%=×100%得,
拉力F的大小为F===1.5×104 N
(4)由于物体的总重由3段绳子承担,所以有3F=G+G动
动滑轮的重力G动=3F-G=3×1.5×104 N-3.6×104 N=9×103 N
当提升质量为4.1 t货箱时,滑轮组的机械效率为
η′=×100%=×100%=×100%=×100%=×100%=82%
4. 解:(1)由图可知,n=3,则绳端移动的距离为
s=nh=3×10 m=30 m
拉力做的功为W=Fs=250 N×30 m=7 500 J,拉力的功率为P===375 W
(2)机械效率为η=×100%=×100%=×100%=×100%=60%
(3)由F=(G+G动)得
动滑轮重力为G动=nF-G=3×250 N-450 N=300 N
能吊起物体的最大重力为G′=nF′-G动=3×400 N-300 N=900 N
滑轮组最大机械效率为η′=×100%=×100%=75%
5. 解:(1)由图可知,承担动滑轮绳子的段数为n=3
水泥运动的速度为v水泥=== m/s
绳子自由端移动的速度v绳=3v水泥=3×m/s=2 m/s
(2)由P===Fv得,电动机对绳子的拉力
F===400 N
(3)有用功为W有用=G水泥h=m水泥gh=2×50 kg×10 N/kg×10 m=1×104 J
电动机做的总功W总=Pt=800 W×15 s=1.2×104 J
滑轮组的机械效率η=×100%=×100%≈83.33%
6. 解:(1)甲对平衡板的压力F甲=G甲=m甲g=55 kg×10 N/kg=550 N,与板的接触面积S=0.05 m2
甲对平衡板的压强p===1.1×104 Pa
(2)提升过程中,平衡板对甲、乙两人的支持力:
F′=G甲+G乙=(m甲+m乙)g=(55 kg+45 kg)×10 N/kg=1 000 N
平衡板将两人提升的高度:h=5 m
①平衡板提升两人所做的功W=F′h=1000 N×5 m=5 000 J
②由图可知,n=2,则拉力所做的总功W总=Fs=2Fh=2×6 250 N×5 m=6.25×104 J
滑轮组做的有用功W有=(G甲+G乙+G板)h=(55 kg+45 kg+900 kg)×10 N/kg×5 m=5×104 J
滑轮组的机械效率η=×100%=×100%=80%
(3)9∶11 【解析】根据杠杆的平衡条件
G甲×OA=G乙×OB
移动后重新平衡时
G甲×(OA+AC)=G乙×(OB+BD)
G甲×OA+G甲×AC=G乙×OB+G乙×BD
G甲×AC=G乙×BD
550 N×AC=450 N×BD
AC∶BD=9∶11
7. 解:(1)已知汽车对绳的拉力F的功率P =120 kW,则t=10 s时间内汽车对绳的拉力做功:
W=Pt=1.2×105 W×10 s=1.2×106 J
(2)汽车拉着货物A沿斜面匀速行驶,速度一定,由题图知,n=3,由P=Fv得汽车对绳的拉力:F====2×104 N
(3)斜面的机械效率为:η=×100%=×100%=×100%=75%
8. 解:(1)物体的体积
V物====4×10-3 m3
则物体浸没在水中时受到的浮力
F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×4×10-3 m3=40 N
(2)物体完全提出水面后,水对容器底减小的压力
ΔF压=F浮=40 N
则物体完全提出水面后,水对容器底减小的压强
Δp压===1 000 Pa
(3)物体浸没在水中匀速上升时,滑轮组的机械效率
η1=×100%
即80%=
解得F=(G物-F浮)=×(200 N-40 N)=600 N
又因为F=3(G物-F浮)+G动
所以G动=F-3(G物-F浮)=600 N-3×(200 N-40 N)=120 N
则物体完全提出水面后,滑轮组的机械效率
η2=×100%=×100%≈83.3%
9. (1)如答图所示
第9题答图
(2)800 320
【解析】(2)由图乙可知,石料完全浸没在水里时所受浮力F浮=3 200 N-2 400 N=800 N;离开水面后绳子拉力T=G石料,所以石料质量m====320 kg.
解:(3)由图乙可知石料从开始运动到完全离开水面用时50 s,则河水的深度h=vt=0.1 m/s×50 s=5 m.根据液体压强公式得:河底受到水的压强p=ρgh=1×103 kg/m3×10 N/kg×5 m=5×104 Pa
(4)石料离开水后,绳子自由端拉力为2 000 N,滑轮组有一个动滑轮,两股绳子承重即n=2,由图乙可知,石料离开水后绳子的拉力T=G=3 200 N,离开水面后滑轮组的机械效率η=×100%=×100%=×100%=×100%=×100%=80%
10. 解:(1)箱子在水底时,下表面的深度为h=5 m,此时箱子下表面受到水的压强:p=ρ水gh=1.0×103 kg/m3×10 N/kg×5 m=5×104 Pa
(2)箱子受到的浮力:F浮=ρ水gV排=1.0×103 kg/m3×10 N/kg×0.2 m3=2×103 N
(3)物体完全露出水面后,已不受浮力,整套装置克服箱子重力做的功是有用功:
W有=G箱h′=m箱gh′=600 kg×10 N/kg×2 m=1.2×104 J
绳子自由端的拉力:F====3 050 N
则拉力所做的总功:
W总=Fs=F·2h=3 050 N×2×2 m=1.22×104 J
则此时滑轮组的机械效率:
η=×100%=×100%≈98%
(4)整个过程中,箱子的运动速度不变,根据P=Fv可知,绳端拉力F最大时,电动机的输出功率最大.当箱子离开水面时,箱子不受浮力作用,此时拉力F最大,F=3 050 N,最大功率为P=Fv绳 =F·2v箱=3 050 N×2×0.5 m/s=3 050 W
(
1
)
