2022-2023学年沪科版数学八年级数下册第18章勾股定理专项练习(含简单答案)
文档属性
| 名称 | 2022-2023学年沪科版数学八年级数下册第18章勾股定理专项练习(含简单答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 386.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-15 18:02:20 | ||
图片预览

文档简介
2022-2023学年下学期沪科版八年级数学勾股定理练习
学校:___________姓名:___________班级:___________分数:___________
一选择题(每小题4分,共40分)
1.下列各组数中,是勾股数的是( )
A.0.3,0.4,5 B.3,4,7 C.5,12,13 D.8,15,16
2..图中字母B代表的正方形的面积为( )
A.12 B.81 C.225 D.144
3.如图,在以下四个正方形网格中,各有一个三角形,不是直角三角形的是( )
A. B. C. D.
4..由下列三条线段组成的三角形中,能构成直角三角形的是( )
A.,, B.,, C.3,4,5 D.,,
5.如图,在四边形中,已知,,且,,则( )
A. B.3 C. D.
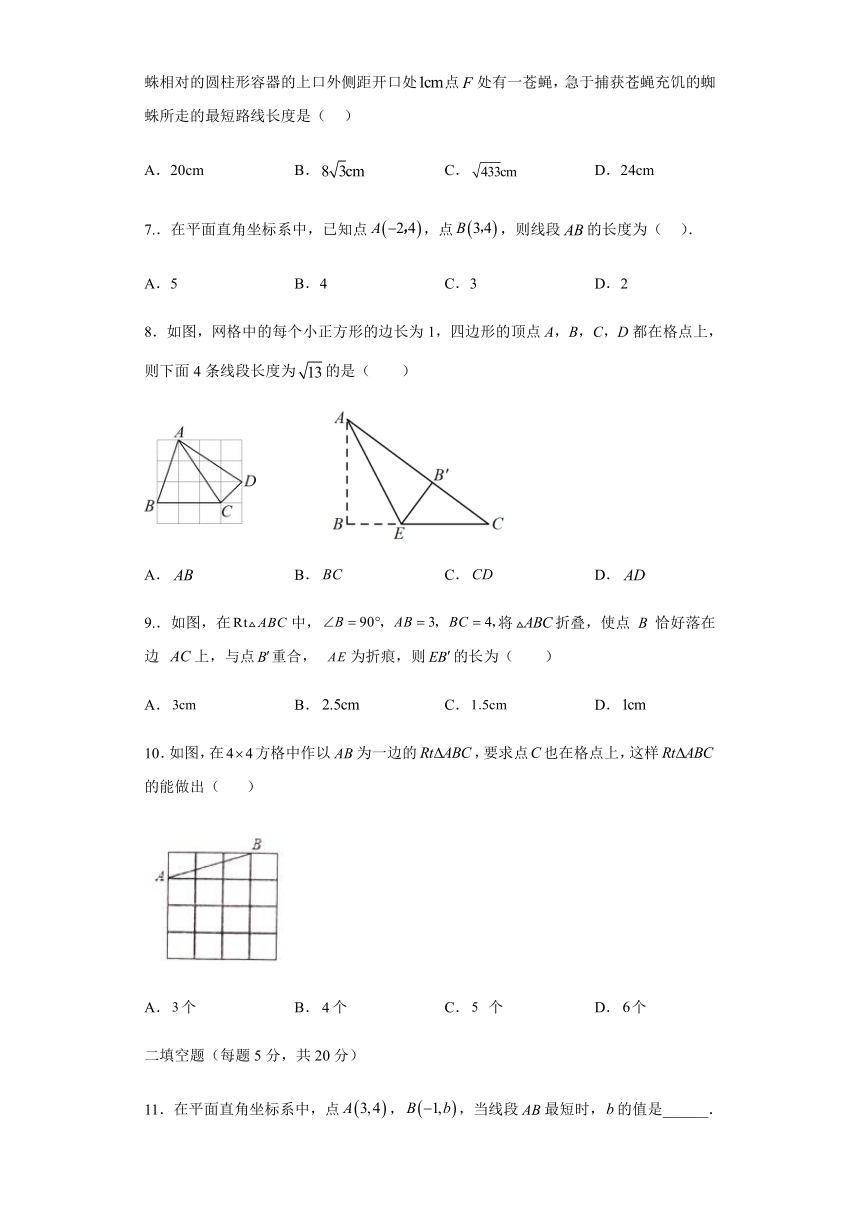
6.如图,圆柱形容器的高,底面周长是,在外侧底面S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处点处有一苍蝇,急于捕获苍蝇充饥的蜘蛛所走的最短路线长度是( )
A.20cm B. C. D.24cm
7..在平面直角坐标系中,已知点,点,则线段的长度为( ).
A.5 B.4 C.3 D.2
8.如图,网格中的每个小正方形的边长为1,四边形的顶点A,B,C,D都在格点上,则下面4条线段长度为的是( )
A. B. C. D.
9..如图,在中,将折叠,使点 B 恰好落在边 上,与点重合, 为折痕,则的长为( )
A. B. C. D.
10.如图,在方格中作以为一边的,要求点也在格点上,这样的能做出( )
A.个 B.个 C. 个 D.个
二填空题(每题5分,共20分)
11.在平面直角坐标系中,点,,当线段最短时,的值是______.
12.如图,山坡上,树甲从点A处折断,其树顶恰好落在另一棵树乙的根部C处,已知AB=4m,BC=10m,已知两棵树的水平距离为6m,则树甲原来高_____.
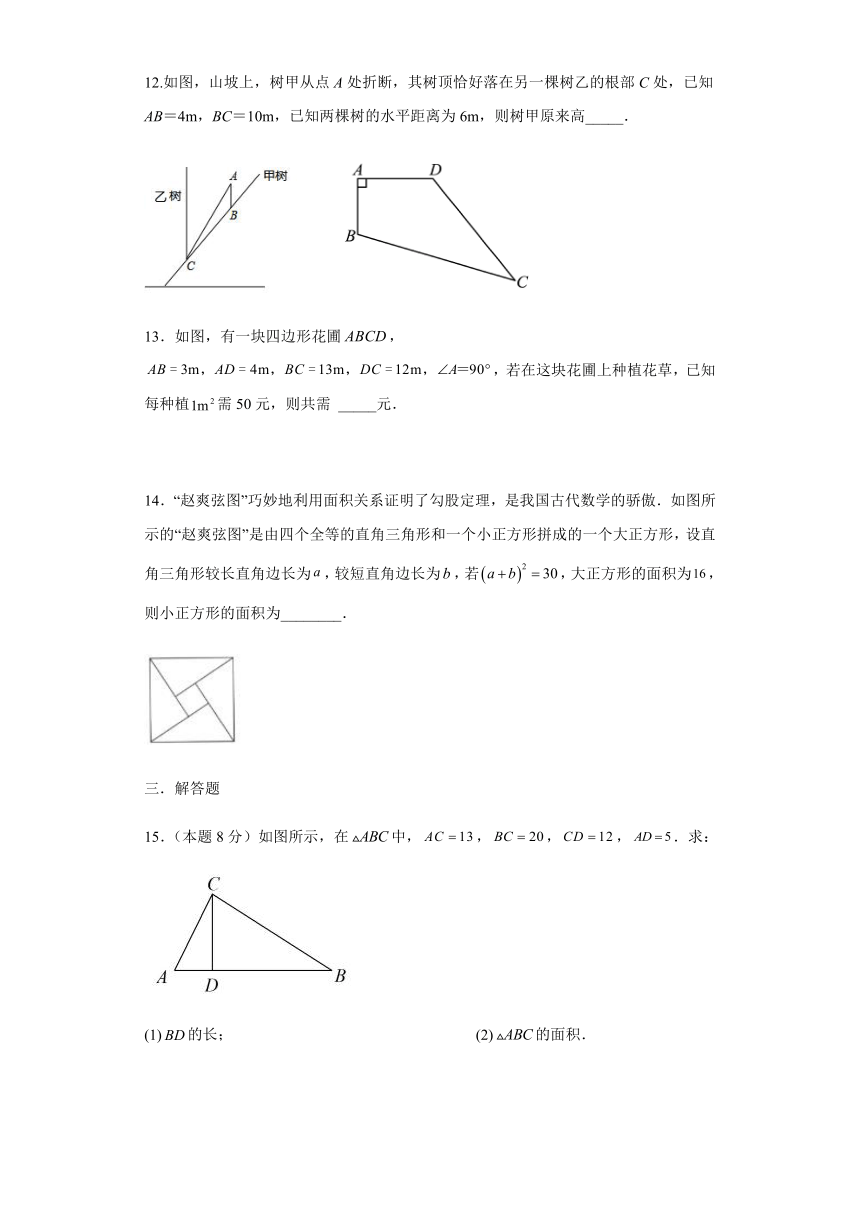
13.如图,有一块四边形花圃,,若在这块花圃上种植花草,已知每种植需50元,则共需 _____元.
14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,大正方形的面积为,则小正方形的面积为________.
解答题
15.(本题8分)如图所示,在中,,,,.求:
(1)的长; (2)的面积.
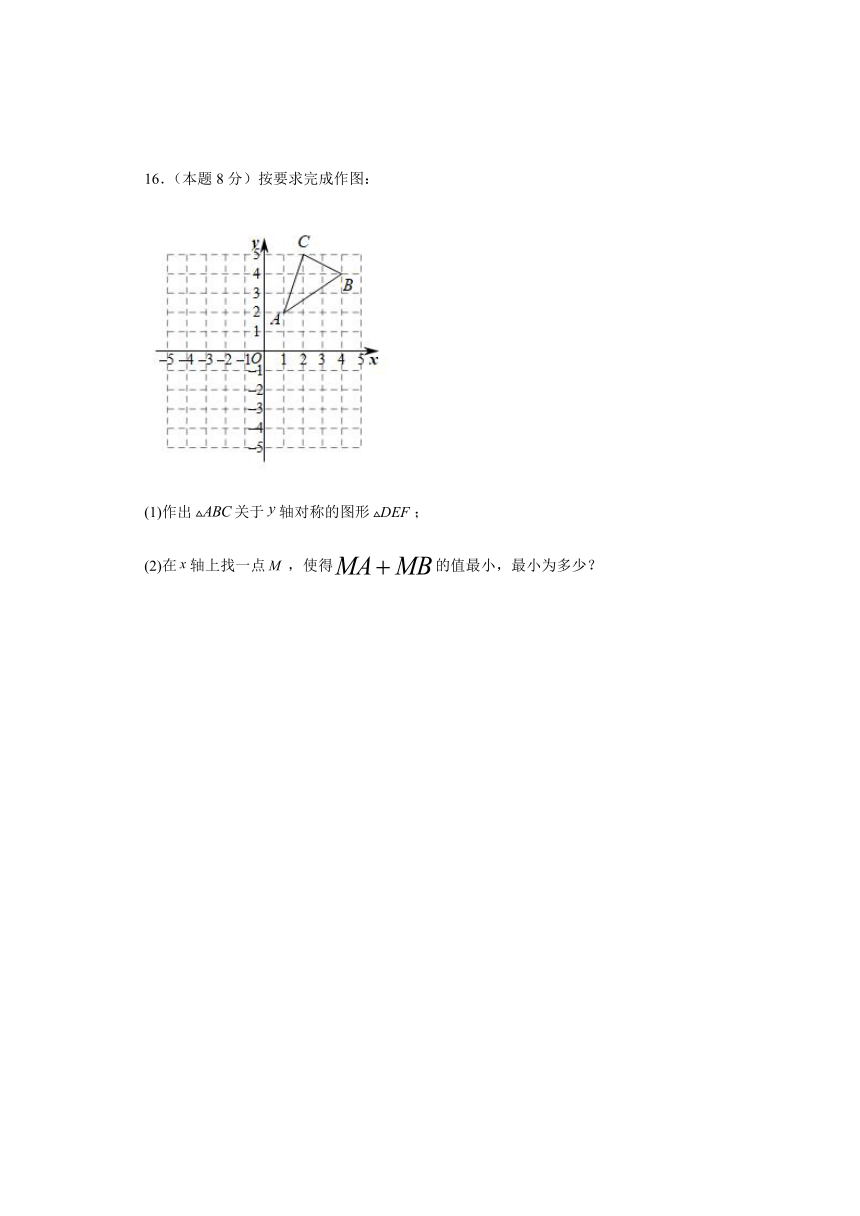
16.(本题8分)按要求完成作图:
(1)作出关于轴对称的图形;
(2)在轴上找一点,使得的值最小,最小为多少?
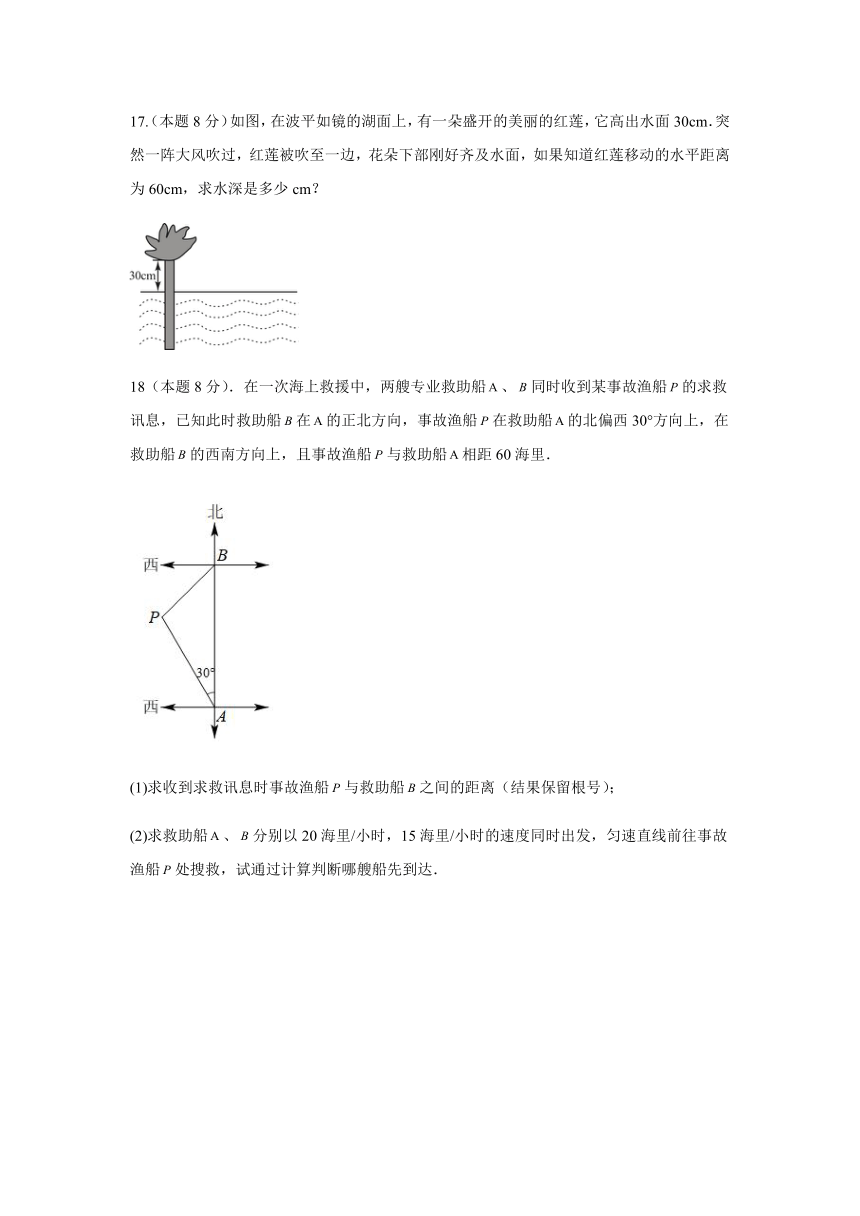
17.(本题8分)如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面30cm.突然一阵大风吹过,红莲被吹至一边,花朵下部刚好齐及水面,如果知道红莲移动的水平距离为60cm,求水深是多少cm?
18(本题8分).在一次海上救援中,两艘专业救助船、同时收到某事故渔船的求救讯息,已知此时救助船在的正北方向,事故渔船在救助船的北偏西30°方向上,在救助船的西南方向上,且事故渔船与救助船相距60海里.
(1)求收到求救讯息时事故渔船与救助船之间的距离(结果保留根号);
(2)求救助船、分别以20海里/小时,15海里/小时的速度同时出发,匀速直线前往事故渔船处搜救,试通过计算判断哪艘船先到达.
19.(本题10分)如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为,货船沿南偏东80°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里,求客船航行的方向.
20.(本题10分)如图,长方形中,cm,cm,将此长方形折叠,使点B与点D重合,折痕为.求的面积.
21.(本题12分)如图,△ABC中,CD⊥AB于D.
(1)图中有几个直角三角形;
(2)若AD=12,AC=13,则CD等于多少;
(3)若CD2=AD·DB, 求证:△ABC是直角三角形.
22.(本题12分)为了鼓励大家积极接种新冠疫苗,某区镇政府采用了移动宣讲的形式进行广播宣传.如图,笔直的公路的一侧点处有一村庄,村庄到公路的距离为,宣讲车周围以内能听到广播宣传,宣讲车在公路上沿方向行驶.
(1)村庄能否听到广播宣传?请说明理由.
(2)已知宣讲车的速度是,如果村庄能听到广播宣传,那么总共能听多长时间?
23.(本题14分)阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三条边长度之间的关系来判断这个三角形的形状:①若,则该三角形是直角三角形;②若,则该三角形是钝角三角形;③若,则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,,故由③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三边长分别是7,8,9,则该三角形是________三角形.
(2)若一个三角形的三边长分别是5,12,x.且这个三角形是直角三角形,求的值.
(3)当,时,判断的形状,并求出对应的的取值范围.
参考答案:
1.A
2.B
3.A
4.C
5.A
6.D
7.D
8.C
9.A
10.C
11.D
12.D
13.(4+6)m
14.1800
15.2
16.
17.45cm
18.(1)海里
(2)救助船先到达,计算过程见解析
19.客船航行的方向为北偏东
20.(1)锐角;(2)169或119;(3)见解析
21.(1)能,理由见解析
(2)
22.(1)2;(2)5;(3)见解析.
23.36.
24.(1)见解析
(2)点M的位置见解析,
25.
26.小鸟至少飞行了10米
27.(1)
(2)
学校:___________姓名:___________班级:___________分数:___________
一选择题(每小题4分,共40分)
1.下列各组数中,是勾股数的是( )
A.0.3,0.4,5 B.3,4,7 C.5,12,13 D.8,15,16
2..图中字母B代表的正方形的面积为( )
A.12 B.81 C.225 D.144
3.如图,在以下四个正方形网格中,各有一个三角形,不是直角三角形的是( )
A. B. C. D.
4..由下列三条线段组成的三角形中,能构成直角三角形的是( )
A.,, B.,, C.3,4,5 D.,,
5.如图,在四边形中,已知,,且,,则( )
A. B.3 C. D.
6.如图,圆柱形容器的高,底面周长是,在外侧底面S处有一蜘蛛,与蜘蛛相对的圆柱形容器的上口外侧距开口处点处有一苍蝇,急于捕获苍蝇充饥的蜘蛛所走的最短路线长度是( )
A.20cm B. C. D.24cm
7..在平面直角坐标系中,已知点,点,则线段的长度为( ).
A.5 B.4 C.3 D.2
8.如图,网格中的每个小正方形的边长为1,四边形的顶点A,B,C,D都在格点上,则下面4条线段长度为的是( )
A. B. C. D.
9..如图,在中,将折叠,使点 B 恰好落在边 上,与点重合, 为折痕,则的长为( )
A. B. C. D.
10.如图,在方格中作以为一边的,要求点也在格点上,这样的能做出( )
A.个 B.个 C. 个 D.个
二填空题(每题5分,共20分)
11.在平面直角坐标系中,点,,当线段最短时,的值是______.
12.如图,山坡上,树甲从点A处折断,其树顶恰好落在另一棵树乙的根部C处,已知AB=4m,BC=10m,已知两棵树的水平距离为6m,则树甲原来高_____.
13.如图,有一块四边形花圃,,若在这块花圃上种植花草,已知每种植需50元,则共需 _____元.
14.“赵爽弦图”巧妙地利用面积关系证明了勾股定理,是我国古代数学的骄傲.如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形,设直角三角形较长直角边长为,较短直角边长为,若,大正方形的面积为,则小正方形的面积为________.
解答题
15.(本题8分)如图所示,在中,,,,.求:
(1)的长; (2)的面积.
16.(本题8分)按要求完成作图:
(1)作出关于轴对称的图形;
(2)在轴上找一点,使得的值最小,最小为多少?
17.(本题8分)如图,在波平如镜的湖面上,有一朵盛开的美丽的红莲,它高出水面30cm.突然一阵大风吹过,红莲被吹至一边,花朵下部刚好齐及水面,如果知道红莲移动的水平距离为60cm,求水深是多少cm?
18(本题8分).在一次海上救援中,两艘专业救助船、同时收到某事故渔船的求救讯息,已知此时救助船在的正北方向,事故渔船在救助船的北偏西30°方向上,在救助船的西南方向上,且事故渔船与救助船相距60海里.
(1)求收到求救讯息时事故渔船与救助船之间的距离(结果保留根号);
(2)求救助船、分别以20海里/小时,15海里/小时的速度同时出发,匀速直线前往事故渔船处搜救,试通过计算判断哪艘船先到达.
19.(本题10分)如图,有一艘货船和一艘客船同时从港口A出发,客船每小时比货船多走5海里,客船与货船速度的比为,货船沿南偏东80°方向航行,2小时后货船到达B处,客船到达C处,若此时两船相距50海里,求客船航行的方向.
20.(本题10分)如图,长方形中,cm,cm,将此长方形折叠,使点B与点D重合,折痕为.求的面积.
21.(本题12分)如图,△ABC中,CD⊥AB于D.
(1)图中有几个直角三角形;
(2)若AD=12,AC=13,则CD等于多少;
(3)若CD2=AD·DB, 求证:△ABC是直角三角形.
22.(本题12分)为了鼓励大家积极接种新冠疫苗,某区镇政府采用了移动宣讲的形式进行广播宣传.如图,笔直的公路的一侧点处有一村庄,村庄到公路的距离为,宣讲车周围以内能听到广播宣传,宣讲车在公路上沿方向行驶.
(1)村庄能否听到广播宣传?请说明理由.
(2)已知宣讲车的速度是,如果村庄能听到广播宣传,那么总共能听多长时间?
23.(本题14分)阅读下列内容:设a,b,c是一个三角形的三条边的长,且a是最长边,我们可以利用a,b,c三条边长度之间的关系来判断这个三角形的形状:①若,则该三角形是直角三角形;②若,则该三角形是钝角三角形;③若,则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,,故由③可知该三角形是锐角三角形,请解答以下问题:
(1)若一个三角形的三边长分别是7,8,9,则该三角形是________三角形.
(2)若一个三角形的三边长分别是5,12,x.且这个三角形是直角三角形,求的值.
(3)当,时,判断的形状,并求出对应的的取值范围.
参考答案:
1.A
2.B
3.A
4.C
5.A
6.D
7.D
8.C
9.A
10.C
11.D
12.D
13.(4+6)m
14.1800
15.2
16.
17.45cm
18.(1)海里
(2)救助船先到达,计算过程见解析
19.客船航行的方向为北偏东
20.(1)锐角;(2)169或119;(3)见解析
21.(1)能,理由见解析
(2)
22.(1)2;(2)5;(3)见解析.
23.36.
24.(1)见解析
(2)点M的位置见解析,
25.
26.小鸟至少飞行了10米
27.(1)
(2)
