18.2 函数图象-平面直角坐标系及函数概念[下学期]
文档属性
| 名称 | 18.2 函数图象-平面直角坐标系及函数概念[下学期] |  | |
| 格式 | rar | ||
| 文件大小 | 195.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2007-10-29 10:33:00 | ||
图片预览




文档简介
课件18张PPT。第三章第一课时:
平面直角坐标系及
函数的概念 要点、考点聚焦
课前热身
典型例题解析
课时训练一. 平面直角坐标系:
1. 有关概念:x(横轴)y(纵轴)o第一象限第二象限第三象限第四象限Pab(a,b)2. 平面内点的坐标:3. 坐标平面内的点与有序
实数对是:一一对应. 坐标平面内的任意一点M,都有唯一一对有序实数(x,y)与它对应;
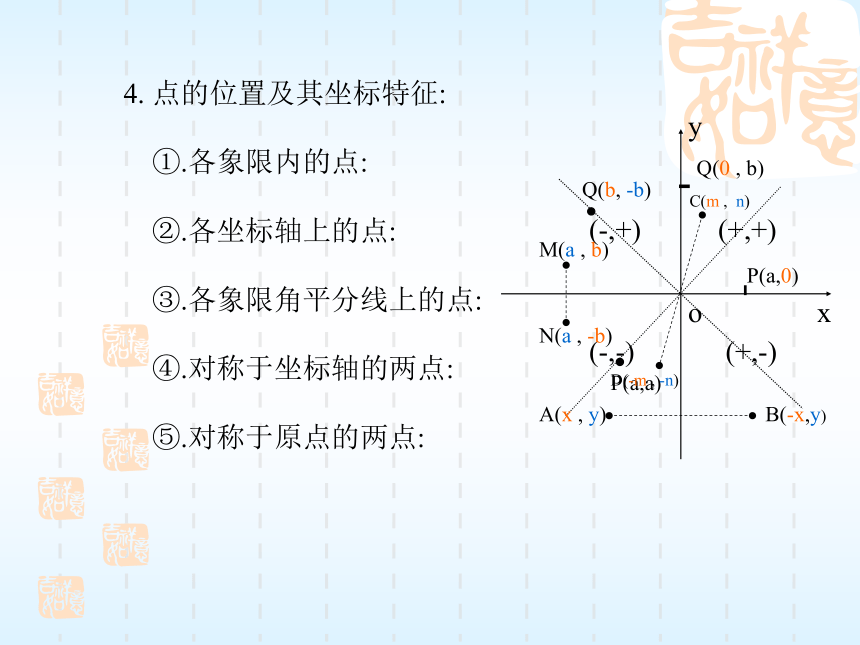
任意一对有序实数(x,y),在坐标平面内都有唯一的点M与它对应.4. 点的位置及其坐标特征:
①.各象限内的点:
②.各坐标轴上的点:
③.各象限角平分线上的点:
④.对称于坐标轴的两点:
⑤.对称于原点的两点:xyo(+,+)(-,+)(-,-)(+,-)P(a,0)Q(0 , b)P(a,a)Q(b, -b)M(a , b)N(a , -b)A(x , y) B(-x,y)C(m , n)D(-m , -n)
1. 意义:
设在一个变化过程中有两个变量 x与y ,
如果对于x的每一个值 , y 都有唯一的值与它
对应 , 就说x是自变量 , y是x的函数. 2.表示法:
(1)解析法(自变量的取值范围).
(2)列表法.
(3)图象法(图象的画法).二. 函数: 确定自变量的取值范围,一般需从两个方面考虑: ( 1)自变量的取值必须使其所在的代数式有意义
(2)如果函数有实际意义,那么必须使实际问题有意义.
1.在平面直角坐标系中,点P(2,1)关于原点对称的点在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限 课前热身C2.已知a 象限。三3.函数 中自变量x的取值
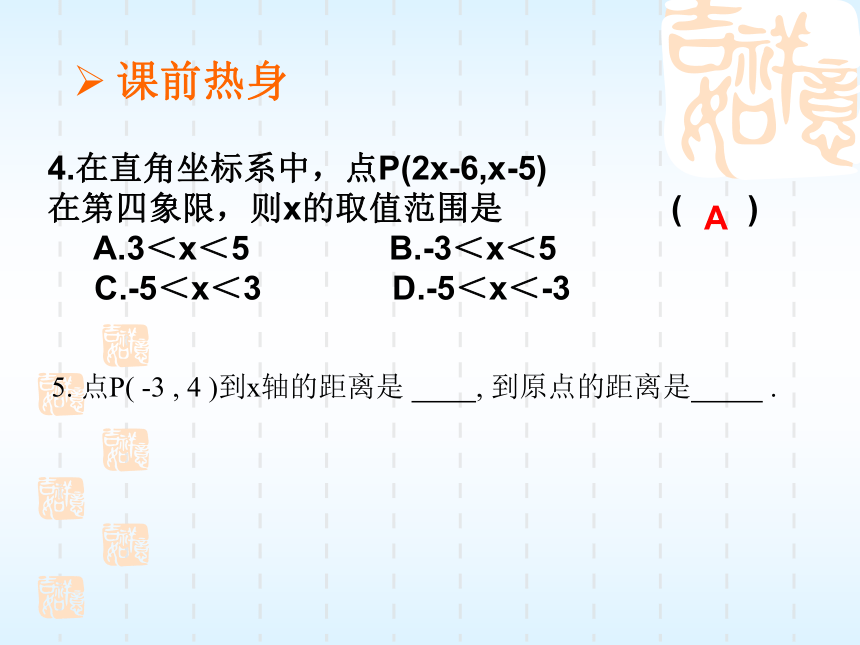
范围是: .x>1/2课前热身4.在直角坐标系中,点P(2x-6,x-5)
在第四象限,则x的取值范围是 ( )
A.3<x<5 B.-3<x<5
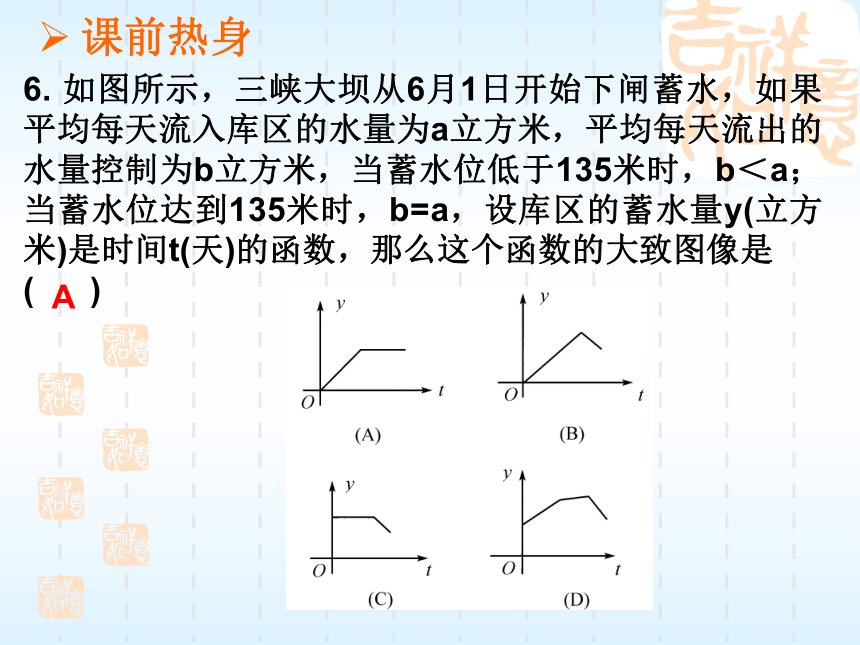
C.-5<x<3 D.-5<x<-3A5. 点P( -3 , 4 )到x轴的距离是 , 到原点的距离是 .课前热身6. 如图所示,三峡大坝从6月1日开始下闸蓄水,如果平均每天流入库区的水量为a立方米,平均每天流出的水量控制为b立方米,当蓄水位低于135米时,b<a;当蓄水位达到135米时,b=a,设库区的蓄水量y(立方米)是时间t(天)的函数,那么这个函数的大致图像是 ( )
A7.星期天晚饭后,小红从家里出去散步,如图3-1-2所示描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系,依据图像,下面描述符合小红散步情景的是 ( )
A.从家出发,到一个公共阅报栏,看了一会儿报,就回家了.
B.从家出发,到了一个公共阅报
栏,看了一会儿报后,继续向前
走了一段,然后回家了.
C.从家出发,一直散步(没有停
留),然后回家了.
D.从家出发,散了一会儿步,
就找同学去了,18分钟后才
开始返回.B课前热身典型例题解析【例1】(1) 在平面直角坐标系中,点
P(-1,1)关于x轴的对称点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限(2)点P(3,-4)关于原点对称的点的坐标是 ( )
A.(3,-4) B.(-3,-4)
C.(3,4) D.(-3,4)(3)平面直角坐标系内,点A(n,1-n)一定
不在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限CDC【例2】 求下列各函数的自变量x的取值范围.
(1)y= ;
(2)y= ;
(3)y= ;
典型例题解析x≠3x≥2x≥2且x≠3解答题:
【例3】.已知 ABC是等边三角形, 边长为2 , 求 ABC各顶 点的坐标.
解:点A 的坐标是(0,0) ,
点B的坐标是(-2,0)
过C点作x轴的垂线 ,垂足为D,
D【例4】 (2003年,武汉市)小强在劳动技术课中要制作一个周长为80cm的等腰三角形,请你写出底边长ycm与一腰长xcm的函数关系式,并求出自变量x的取值范围.
解:y=80-2x
∵两边之和大于第三边且两边之差小于第三边
∴x-x<y<x+x∴0<80-2x<2x
即20<x<40
∴y=80-2x(20<x<40)典型例题解析1.思考问题不慎密,对于有些该分类讨论的问题,没
有按几种情况分别研究,出现漏解现象.
2.对于具有实际意义问题的函数,求自变量的取值范
围时,容易因考虑问题不慎密,遗漏隐含条件而导致
错误.方法小结:课时训练1.(2004年·四川省)在函数 中,自变量x的取值范围是 ( )
A.x≠-1 B.x≠0 C.x≤-1 D.x≥-1A2.(2004年·黑龙江)在平面直角坐标系内,A、B、C三点坐标分别是(0,0)(4,0)(3,2),以A、B、C三点为顶点画平行四边形,则第四个顶点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限CA3.(2004年·广州)点P在第二象限,若该点到x轴的距离为 ,到y轴的距离为1,则点P的坐标是 ( )
A.( )B.( )C.( )D.( ) 课时训练4.(2004年·哈尔滨)坐标平面内点A(m,n)在第四象限,那么点B(n,m)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限B5.(2003年·山西省)函数y= 中的自变量x的取值范围 . x≥-3且x≠±26.(2003年·四川省)如图所示,小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度继续匀速行驶,下面是行驶路程s(米)关于时间t(分)的函数图像,那么符合小明行驶情况的图像大致是
( )C课时训练7.如图所示是某蓄水池的横断面示意图,分深水区和
浅水区,如果这个蓄水池以固定的流量注水,下面哪
个图像能大致表示水的最大深度h和时间t之间的关系?
( ) C课时训练再见!
平面直角坐标系及
函数的概念 要点、考点聚焦
课前热身
典型例题解析
课时训练一. 平面直角坐标系:
1. 有关概念:x(横轴)y(纵轴)o第一象限第二象限第三象限第四象限Pab(a,b)2. 平面内点的坐标:3. 坐标平面内的点与有序
实数对是:一一对应. 坐标平面内的任意一点M,都有唯一一对有序实数(x,y)与它对应;
任意一对有序实数(x,y),在坐标平面内都有唯一的点M与它对应.4. 点的位置及其坐标特征:
①.各象限内的点:
②.各坐标轴上的点:
③.各象限角平分线上的点:
④.对称于坐标轴的两点:
⑤.对称于原点的两点:xyo(+,+)(-,+)(-,-)(+,-)P(a,0)Q(0 , b)P(a,a)Q(b, -b)M(a , b)N(a , -b)A(x , y) B(-x,y)C(m , n)D(-m , -n)
1. 意义:
设在一个变化过程中有两个变量 x与y ,
如果对于x的每一个值 , y 都有唯一的值与它
对应 , 就说x是自变量 , y是x的函数. 2.表示法:
(1)解析法(自变量的取值范围).
(2)列表法.
(3)图象法(图象的画法).二. 函数: 确定自变量的取值范围,一般需从两个方面考虑: ( 1)自变量的取值必须使其所在的代数式有意义
(2)如果函数有实际意义,那么必须使实际问题有意义.
1.在平面直角坐标系中,点P(2,1)关于原点对称的点在 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限 课前热身C2.已知a
范围是: .x>1/2课前热身4.在直角坐标系中,点P(2x-6,x-5)
在第四象限,则x的取值范围是 ( )
A.3<x<5 B.-3<x<5
C.-5<x<3 D.-5<x<-3A5. 点P( -3 , 4 )到x轴的距离是 , 到原点的距离是 .课前热身6. 如图所示,三峡大坝从6月1日开始下闸蓄水,如果平均每天流入库区的水量为a立方米,平均每天流出的水量控制为b立方米,当蓄水位低于135米时,b<a;当蓄水位达到135米时,b=a,设库区的蓄水量y(立方米)是时间t(天)的函数,那么这个函数的大致图像是 ( )
A7.星期天晚饭后,小红从家里出去散步,如图3-1-2所示描述了她散步过程中离家的距离s(米)与散步所用时间t(分)之间的函数关系,依据图像,下面描述符合小红散步情景的是 ( )
A.从家出发,到一个公共阅报栏,看了一会儿报,就回家了.
B.从家出发,到了一个公共阅报
栏,看了一会儿报后,继续向前
走了一段,然后回家了.
C.从家出发,一直散步(没有停
留),然后回家了.
D.从家出发,散了一会儿步,
就找同学去了,18分钟后才
开始返回.B课前热身典型例题解析【例1】(1) 在平面直角坐标系中,点
P(-1,1)关于x轴的对称点在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限(2)点P(3,-4)关于原点对称的点的坐标是 ( )
A.(3,-4) B.(-3,-4)
C.(3,4) D.(-3,4)(3)平面直角坐标系内,点A(n,1-n)一定
不在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限CDC【例2】 求下列各函数的自变量x的取值范围.
(1)y= ;
(2)y= ;
(3)y= ;
典型例题解析x≠3x≥2x≥2且x≠3解答题:
【例3】.已知 ABC是等边三角形, 边长为2 , 求 ABC各顶 点的坐标.
解:点A 的坐标是(0,0) ,
点B的坐标是(-2,0)
过C点作x轴的垂线 ,垂足为D,
D【例4】 (2003年,武汉市)小强在劳动技术课中要制作一个周长为80cm的等腰三角形,请你写出底边长ycm与一腰长xcm的函数关系式,并求出自变量x的取值范围.
解:y=80-2x
∵两边之和大于第三边且两边之差小于第三边
∴x-x<y<x+x∴0<80-2x<2x
即20<x<40
∴y=80-2x(20<x<40)典型例题解析1.思考问题不慎密,对于有些该分类讨论的问题,没
有按几种情况分别研究,出现漏解现象.
2.对于具有实际意义问题的函数,求自变量的取值范
围时,容易因考虑问题不慎密,遗漏隐含条件而导致
错误.方法小结:课时训练1.(2004年·四川省)在函数 中,自变量x的取值范围是 ( )
A.x≠-1 B.x≠0 C.x≤-1 D.x≥-1A2.(2004年·黑龙江)在平面直角坐标系内,A、B、C三点坐标分别是(0,0)(4,0)(3,2),以A、B、C三点为顶点画平行四边形,则第四个顶点不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限CA3.(2004年·广州)点P在第二象限,若该点到x轴的距离为 ,到y轴的距离为1,则点P的坐标是 ( )
A.( )B.( )C.( )D.( ) 课时训练4.(2004年·哈尔滨)坐标平面内点A(m,n)在第四象限,那么点B(n,m)在 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限B5.(2003年·山西省)函数y= 中的自变量x的取值范围 . x≥-3且x≠±26.(2003年·四川省)如图所示,小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快了骑车速度继续匀速行驶,下面是行驶路程s(米)关于时间t(分)的函数图像,那么符合小明行驶情况的图像大致是
( )C课时训练7.如图所示是某蓄水池的横断面示意图,分深水区和
浅水区,如果这个蓄水池以固定的流量注水,下面哪
个图像能大致表示水的最大深度h和时间t之间的关系?
( ) C课时训练再见!
