第16章 分式复习 习题课件(共30张PPT)
文档属性
| 名称 | 第16章 分式复习 习题课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 492.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 21:05:13 | ||
图片预览










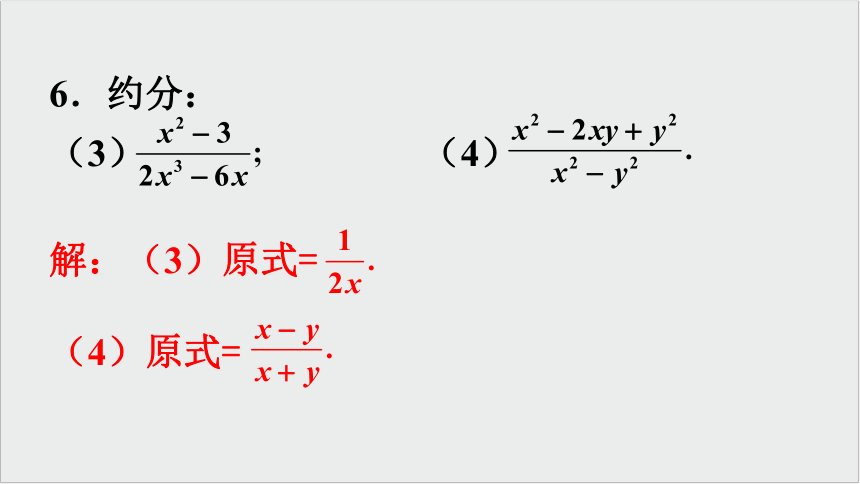

文档简介
(共30张PPT)
八(下)数学教材习题
第16章
1.填空:
(1)某梨园m平方米产梨n千克,平均每平方米产梨 千克;
(2)某工厂原计划a天完成b件产品,现在需要提前n天完成,每天要比原来多生产产品 件;
(3)德国著名物理学家普朗克发现:
能量子=h×频率.这里的h被称为普朗克常数,约为0.000000000000000000000000000000000663焦 秒,用科学记数法可简洁地记
为 焦 秒;
6.63×10-34
(4)一种微粒的半径是4×10-5米,用小数表示为 米;
(5)一个纳米粒子的直径是35纳米,若用科学记数法表示,则为 米.
0.00004
3.5×10-8
2.计算:
(1) (2)0.01-1;
(3)5-2; (4)(-0.1)-2.
解:(1)原式=1.
(2)原式=100.
(3)原式= .
(4)原式=100.
3.用科学记数法表示下列各数;
(1)100000;(2)0.00001;
(3)-112000;(4)-0.000112.
解:(1)原式=105.
(2)原式=10-5.
(3)原式=-1.12×105.
(4)原式=-1.12×10-4.
4.把下列各有理式分别填入相应的圈中:
…
整式
…
分式
5.写出下列各等式中未知的分子或分母:
(1) (2)
解:(1)
(2)
5.写出下列各等式中未知的分子或分母:
(3) (4)
解:(3)
(4)
6.约分:
(1) (2)
解:(1)原式=
(2)原式=
6.约分:
(3) (4)
解:(3)原式=
(4)原式=
7.通分:
(1) (2)
解:(1)最简公分母为abx,
(2)最简公分母为y(a-x),
7.通分:
(3) (4)
解:(3)
(4)
8.计算:
(1) (2)
解:(1)原式=
(2)原式=
8.计算:
(3) (4)
解:(3)原式=
(4)原式=
9.解下列分式方程:
(1)
解:方程两边同乘6(x+1),
得6+3(x+1)=5(x+1).
解得x=2.
检验:当x=2时,6(x+1)≠0,
故原分式方程的解是x=2.
9.解下列分式方程:
(2)
解:方程两边同乘(x-2)(x-3),
得2(x-2)=3(x-3).
解得x=5.
检验:当x=5时,(x-2)(x-3)≠0,
故原分式方程的解是x=5.
9.解下列分式方程:
(3)
解:方程两边同乘(x2+5x-6)(x2+x+6),得x2+x+6=x2+5x-6.
解得x=3.
检验:当x=3时,(x2+5x-6)(x2+x+6)≠0,
故原分式方程的解是x=3.
10.某校n名学生参加市法律知识竞赛,他们的成绩分别为a1,a2,…,an,这n名学生的平均成绩为多少?
解:(a1+a2+…+an)÷n=
答:这n名学生的平均成绩为
11.甲、乙两辆汽车分别从A、B两城同时沿高速公路驶向C城.已知A、C两城的路程为450千米,B、C两城的路程为400千米,甲车比乙车的速度快10千米/时,结果两辆车同时到达C城.求两车的速度.
解:设甲车的速度是x千米/时,则乙车的速度是(x-10)千米/时.
依题意得 解得x=90.
经检验,x=90是原方程的解.则x-10=80.
答:甲车的速度是90千米/时,乙车的速度是80千米/时.
12.计算:
(1) (2)
解:(1)原式=
(2)原式=
12.计算:
(3)
(4)
解:(3)原式=
(4)原式=
13.某服装制造厂要在开学前赶制3000套校服,为了尽快完成任务,厂领导合理调配,加强第一线人力,使每天完成的校服比原计划多了20%,结果提前4天完成任务.问原计划每天能完成多少套校服?
解:设原计划每天能完成x套校服,则调配后每天能完成(1+20%)x套校服.
由题意得 解得x=125.
经检验,x=125是原分式方程的解,且符合题意.
答:原计划每天能完成125套校服.
14.一辆货车送货上山,并按原路下山,上山速度为a千米/时,下山速度为b千米/时,求货车上、下山的平均速度.
解:设货车上山的路程为x千米,则上山的时间为
小时,下山的时间为 小时,
∴上、下山的平均速度为 (千米/时).
答:货车上、下山的平均速度为 千米/时.
15.(1)已知 ,求 的值;
(2)已知 ,求 的值.
解:(1)
(2)
16.观察下面依次排列的一串单项式:
x,-2x2,4x3,-8x4,16x5,…
(1)从第二个单项式起,计算每一个单项式与它前面的单项式的商,你有什么发现?
解:-2x2÷x=-2x,4x3÷(-2x2)=-2x,
-8x4÷4x3=-2x,16x5÷(-8x4)=-2x,…
所以从第二个单项式起,每一个单项式与它前面的单项式的商都是-2x.
(2)如果按你发现的规律继续写下去,第10个单项式是什么?
解:按发现的规律可知:
x,-2x2,4x3=(-2)2x3,-8x4=(-2)3x4,
16x5=(-2)4x5,…,(-2)n-1xn,…
所以第10个单项式是(-2)9x10=-512x10.
八(下)数学教材习题
第16章
1.填空:
(1)某梨园m平方米产梨n千克,平均每平方米产梨 千克;
(2)某工厂原计划a天完成b件产品,现在需要提前n天完成,每天要比原来多生产产品 件;
(3)德国著名物理学家普朗克发现:
能量子=h×频率.这里的h被称为普朗克常数,约为0.000000000000000000000000000000000663焦 秒,用科学记数法可简洁地记
为 焦 秒;
6.63×10-34
(4)一种微粒的半径是4×10-5米,用小数表示为 米;
(5)一个纳米粒子的直径是35纳米,若用科学记数法表示,则为 米.
0.00004
3.5×10-8
2.计算:
(1) (2)0.01-1;
(3)5-2; (4)(-0.1)-2.
解:(1)原式=1.
(2)原式=100.
(3)原式= .
(4)原式=100.
3.用科学记数法表示下列各数;
(1)100000;(2)0.00001;
(3)-112000;(4)-0.000112.
解:(1)原式=105.
(2)原式=10-5.
(3)原式=-1.12×105.
(4)原式=-1.12×10-4.
4.把下列各有理式分别填入相应的圈中:
…
整式
…
分式
5.写出下列各等式中未知的分子或分母:
(1) (2)
解:(1)
(2)
5.写出下列各等式中未知的分子或分母:
(3) (4)
解:(3)
(4)
6.约分:
(1) (2)
解:(1)原式=
(2)原式=
6.约分:
(3) (4)
解:(3)原式=
(4)原式=
7.通分:
(1) (2)
解:(1)最简公分母为abx,
(2)最简公分母为y(a-x),
7.通分:
(3) (4)
解:(3)
(4)
8.计算:
(1) (2)
解:(1)原式=
(2)原式=
8.计算:
(3) (4)
解:(3)原式=
(4)原式=
9.解下列分式方程:
(1)
解:方程两边同乘6(x+1),
得6+3(x+1)=5(x+1).
解得x=2.
检验:当x=2时,6(x+1)≠0,
故原分式方程的解是x=2.
9.解下列分式方程:
(2)
解:方程两边同乘(x-2)(x-3),
得2(x-2)=3(x-3).
解得x=5.
检验:当x=5时,(x-2)(x-3)≠0,
故原分式方程的解是x=5.
9.解下列分式方程:
(3)
解:方程两边同乘(x2+5x-6)(x2+x+6),得x2+x+6=x2+5x-6.
解得x=3.
检验:当x=3时,(x2+5x-6)(x2+x+6)≠0,
故原分式方程的解是x=3.
10.某校n名学生参加市法律知识竞赛,他们的成绩分别为a1,a2,…,an,这n名学生的平均成绩为多少?
解:(a1+a2+…+an)÷n=
答:这n名学生的平均成绩为
11.甲、乙两辆汽车分别从A、B两城同时沿高速公路驶向C城.已知A、C两城的路程为450千米,B、C两城的路程为400千米,甲车比乙车的速度快10千米/时,结果两辆车同时到达C城.求两车的速度.
解:设甲车的速度是x千米/时,则乙车的速度是(x-10)千米/时.
依题意得 解得x=90.
经检验,x=90是原方程的解.则x-10=80.
答:甲车的速度是90千米/时,乙车的速度是80千米/时.
12.计算:
(1) (2)
解:(1)原式=
(2)原式=
12.计算:
(3)
(4)
解:(3)原式=
(4)原式=
13.某服装制造厂要在开学前赶制3000套校服,为了尽快完成任务,厂领导合理调配,加强第一线人力,使每天完成的校服比原计划多了20%,结果提前4天完成任务.问原计划每天能完成多少套校服?
解:设原计划每天能完成x套校服,则调配后每天能完成(1+20%)x套校服.
由题意得 解得x=125.
经检验,x=125是原分式方程的解,且符合题意.
答:原计划每天能完成125套校服.
14.一辆货车送货上山,并按原路下山,上山速度为a千米/时,下山速度为b千米/时,求货车上、下山的平均速度.
解:设货车上山的路程为x千米,则上山的时间为
小时,下山的时间为 小时,
∴上、下山的平均速度为 (千米/时).
答:货车上、下山的平均速度为 千米/时.
15.(1)已知 ,求 的值;
(2)已知 ,求 的值.
解:(1)
(2)
16.观察下面依次排列的一串单项式:
x,-2x2,4x3,-8x4,16x5,…
(1)从第二个单项式起,计算每一个单项式与它前面的单项式的商,你有什么发现?
解:-2x2÷x=-2x,4x3÷(-2x2)=-2x,
-8x4÷4x3=-2x,16x5÷(-8x4)=-2x,…
所以从第二个单项式起,每一个单项式与它前面的单项式的商都是-2x.
(2)如果按你发现的规律继续写下去,第10个单项式是什么?
解:按发现的规律可知:
x,-2x2,4x3=(-2)2x3,-8x4=(-2)3x4,
16x5=(-2)4x5,…,(-2)n-1xn,…
所以第10个单项式是(-2)9x10=-512x10.
