山东省聊城市2022-2023学年八年级上学期期末数学试题(无答案)
文档属性
| 名称 | 山东省聊城市2022-2023学年八年级上学期期末数学试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 313.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-14 20:31:49 | ||
图片预览

文档简介
2022-2023学年度第一学期期末学业水平检测
八年级数学试题
(时间:120分钟;满分:120分)
一、选择题(每题3分,共36分)
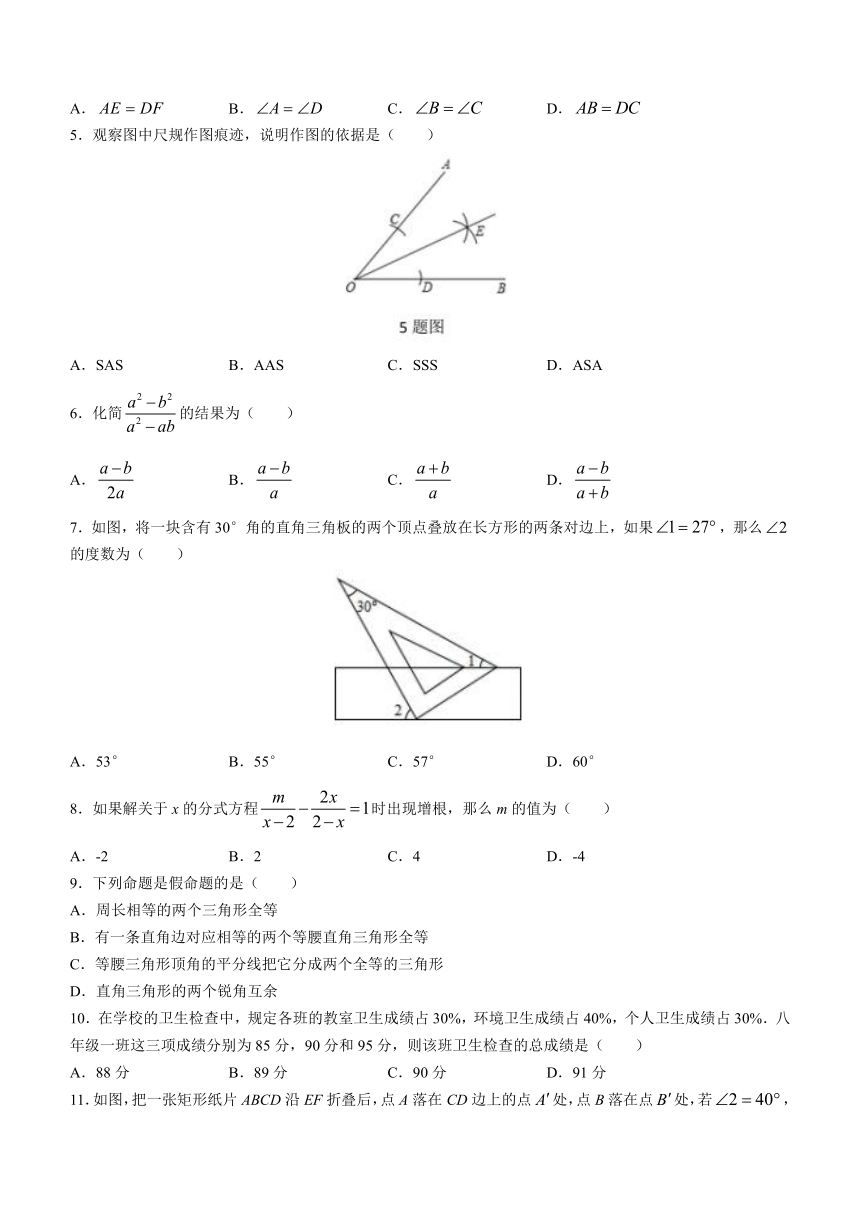
1.下列四个图案中,不是轴对称图形的是( )
A. B.
C. D.
2.如果分式的值为0,那么x的值为( )
A.-1 B.1 C.-1或1 D.1或0
3.某车间20名工人日加工零件数如表所示:
日加工零件数 4 5 6 7 8
人数 2 6 5 4 3
这些工人日加工零件数的众数、中位数分别是( )
A.5、6 B.5、5 C.6、5 D.6、6
4.如图,,,,要根据“HL”证明,则还需要添加一个条件是( )
A. B. C. D.
5.观察图中尺规作图痕迹,说明作图的依据是( )
A.SAS B.AAS C.SSS D.ASA
6.化简的结果为( )
A. B. C. D.
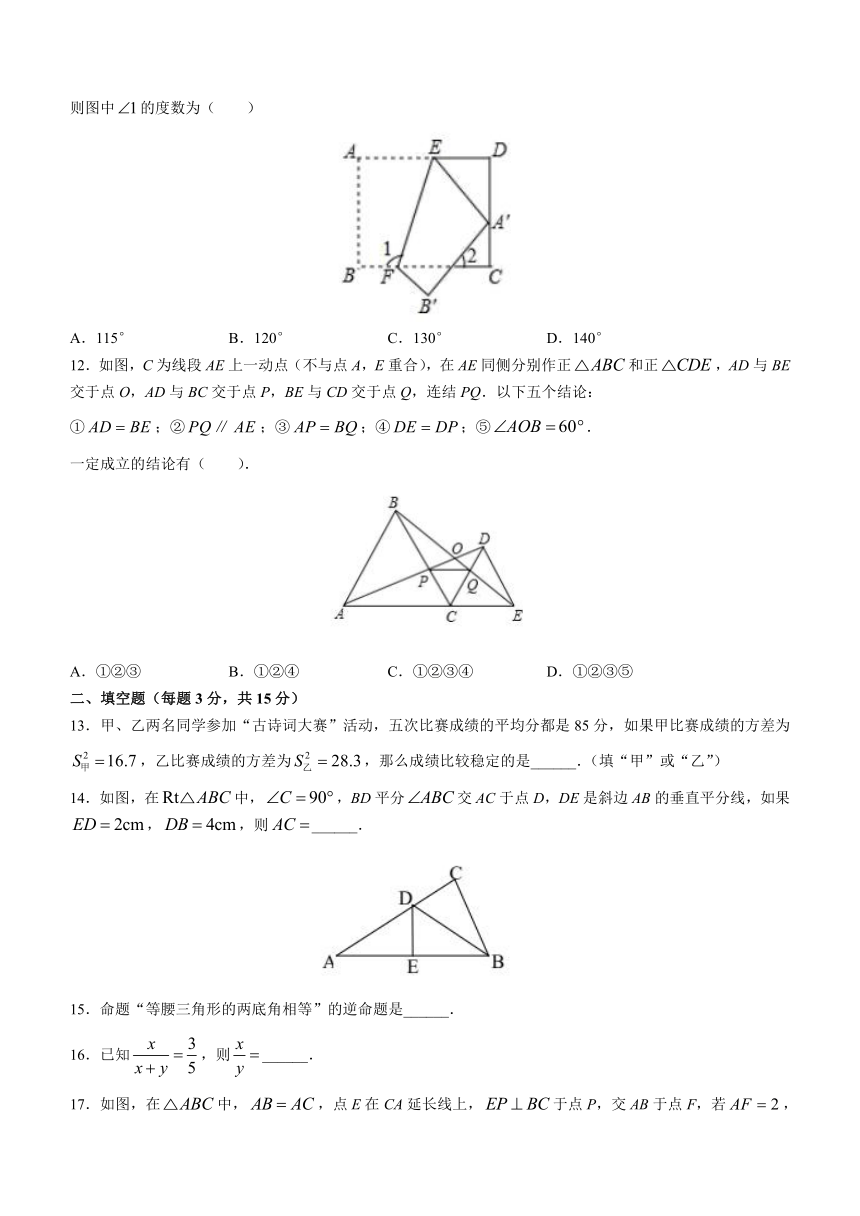
7.如图,将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上,如果,那么的度数为( )
A.53° B.55° C.57° D.60°
8.如果解关于x的分式方程时出现增根,那么m的值为( )
A.-2 B.2 C.4 D.-4
9.下列命题是假命题的是( )
A.周长相等的两个三角形全等
B.有一条直角边对应相等的两个等腰直角三角形全等
C.等腰三角形顶角的平分线把它分成两个全等的三角形
D.直角三角形的两个锐角互余
10.在学校的卫生检查中,规定各班的教室卫生成绩占30%,环境卫生成绩占40%,个人卫生成绩占30%.八年级一班这三项成绩分别为85分,90分和95分,则该班卫生检查的总成绩是( )
A.88分 B.89分 C.90分 D.91分
11.如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点处,点B落在点处,若,则图中的度数为( )
A.115° B.120° C.130° D.140°
12.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正和正,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:
①;②;③;④;⑤.
一定成立的结论有( ).
A.①②③ B.①②④ C.①②③④ D.①②③⑤
二、填空题(每题3分,共15分)
13.甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为,乙比赛成绩的方差为,那么成绩比较稳定的是______.(填“甲”或“乙”)
14.如图,在中,,BD平分交AC于点D,DE是斜边AB的垂直平分线,如果,,则______.
15.命题“等腰三角形的两底角相等”的逆命题是______.
16.已知,则______.
17.如图,在中,,点E在CA延长线上,于点P,交AB于点F,若,,则CE的长度为______.
三、解答题(共69分)
18.(共7分)
(1)计算:
(2)先化简,然后从的范围内选取一个合适的整数作为a的值代入求值.
19.(共8分)解分式方程
(1) (2)
20.(8分)在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,的顶点均在格点上,点A的坐标是.
(1)在图中作出关于x轴的对称图形;
(2)画出关于y轴对称的,并写出点的坐标;
(3)在x轴上找一点P,使得周长最小.
21.(6分)如图,已知,点E是DF的中点.,,求BD的长.
22.(10分)阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
已知:如图,,BE,DF分别平分,,且.
求证:.
证明:∵BE,DF分别平分,( ① ),∴,( ② ).
∵( ③ ),∴( ④ ).
∴( ⑤ ).
∵( ⑥ ),∴( ⑦ ).
∴( ⑧ ).
∴,( ⑨ ).
∴( ⑩ ).
23.(8分)在“母亲节”前夕,某花店用16000元购进第一批礼盒鲜花,上市后很快预售一空.根据市场需求情况,该花店又用7500元购进第二批礼盒鲜花.已知第二批所购鲜花的盒数是第一批所购鲜花的,且每盒鲜花的进价比第一批的进价少10元.问第二批鲜花每盒的进价是多少元?
24.(10分)如图,OC平分,于D,于E,连接DE.
(1)求证:;
(2)猜想DE与OC的位置关系?并说明理由.
25.(12分)如图(1),,,点C是BD上一点,且,.
(1)试判断AC与CE的位置关系,并说明理由.
(2)如图(2),若把沿直线BD向左平移,使的顶点C与B重合,此时第(1)问中AC与BE的位置关系还成立吗?说明理由.(注意字母的变化).
八年级数学试题
(时间:120分钟;满分:120分)
一、选择题(每题3分,共36分)
1.下列四个图案中,不是轴对称图形的是( )
A. B.
C. D.
2.如果分式的值为0,那么x的值为( )
A.-1 B.1 C.-1或1 D.1或0
3.某车间20名工人日加工零件数如表所示:
日加工零件数 4 5 6 7 8
人数 2 6 5 4 3
这些工人日加工零件数的众数、中位数分别是( )
A.5、6 B.5、5 C.6、5 D.6、6
4.如图,,,,要根据“HL”证明,则还需要添加一个条件是( )
A. B. C. D.
5.观察图中尺规作图痕迹,说明作图的依据是( )
A.SAS B.AAS C.SSS D.ASA
6.化简的结果为( )
A. B. C. D.
7.如图,将一块含有30°角的直角三角板的两个顶点叠放在长方形的两条对边上,如果,那么的度数为( )
A.53° B.55° C.57° D.60°
8.如果解关于x的分式方程时出现增根,那么m的值为( )
A.-2 B.2 C.4 D.-4
9.下列命题是假命题的是( )
A.周长相等的两个三角形全等
B.有一条直角边对应相等的两个等腰直角三角形全等
C.等腰三角形顶角的平分线把它分成两个全等的三角形
D.直角三角形的两个锐角互余
10.在学校的卫生检查中,规定各班的教室卫生成绩占30%,环境卫生成绩占40%,个人卫生成绩占30%.八年级一班这三项成绩分别为85分,90分和95分,则该班卫生检查的总成绩是( )
A.88分 B.89分 C.90分 D.91分
11.如图,把一张矩形纸片ABCD沿EF折叠后,点A落在CD边上的点处,点B落在点处,若,则图中的度数为( )
A.115° B.120° C.130° D.140°
12.如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作正和正,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ.以下五个结论:
①;②;③;④;⑤.
一定成立的结论有( ).
A.①②③ B.①②④ C.①②③④ D.①②③⑤
二、填空题(每题3分,共15分)
13.甲、乙两名同学参加“古诗词大赛”活动,五次比赛成绩的平均分都是85分,如果甲比赛成绩的方差为,乙比赛成绩的方差为,那么成绩比较稳定的是______.(填“甲”或“乙”)
14.如图,在中,,BD平分交AC于点D,DE是斜边AB的垂直平分线,如果,,则______.
15.命题“等腰三角形的两底角相等”的逆命题是______.
16.已知,则______.
17.如图,在中,,点E在CA延长线上,于点P,交AB于点F,若,,则CE的长度为______.
三、解答题(共69分)
18.(共7分)
(1)计算:
(2)先化简,然后从的范围内选取一个合适的整数作为a的值代入求值.
19.(共8分)解分式方程
(1) (2)
20.(8分)在如图所示的直角坐标系中,每个小方格都是边长为1的正方形,的顶点均在格点上,点A的坐标是.
(1)在图中作出关于x轴的对称图形;
(2)画出关于y轴对称的,并写出点的坐标;
(3)在x轴上找一点P,使得周长最小.
21.(6分)如图,已知,点E是DF的中点.,,求BD的长.
22.(10分)阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
已知:如图,,BE,DF分别平分,,且.
求证:.
证明:∵BE,DF分别平分,( ① ),∴,( ② ).
∵( ③ ),∴( ④ ).
∴( ⑤ ).
∵( ⑥ ),∴( ⑦ ).
∴( ⑧ ).
∴,( ⑨ ).
∴( ⑩ ).
23.(8分)在“母亲节”前夕,某花店用16000元购进第一批礼盒鲜花,上市后很快预售一空.根据市场需求情况,该花店又用7500元购进第二批礼盒鲜花.已知第二批所购鲜花的盒数是第一批所购鲜花的,且每盒鲜花的进价比第一批的进价少10元.问第二批鲜花每盒的进价是多少元?
24.(10分)如图,OC平分,于D,于E,连接DE.
(1)求证:;
(2)猜想DE与OC的位置关系?并说明理由.
25.(12分)如图(1),,,点C是BD上一点,且,.
(1)试判断AC与CE的位置关系,并说明理由.
(2)如图(2),若把沿直线BD向左平移,使的顶点C与B重合,此时第(1)问中AC与BE的位置关系还成立吗?说明理由.(注意字母的变化).
同课章节目录
