平面直角坐标系[下学期]
图片预览





文档简介
课件26张PPT。函数的图象1.平面直角坐标系 如图是一条数轴,数轴上的点与实数是一一对应的.数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标 例如,点A在数轴上的坐标是4,点B在数轴上的坐标是-2.5.知道一个点的坐标,这个点的位置就确定了.问 题 情 境(2)在数轴上画出下列实数对应的点
-1, 2.5 , 0, 0.5问题1 你去过电影院吗?还记得在电影院是怎么找座位的吗?解
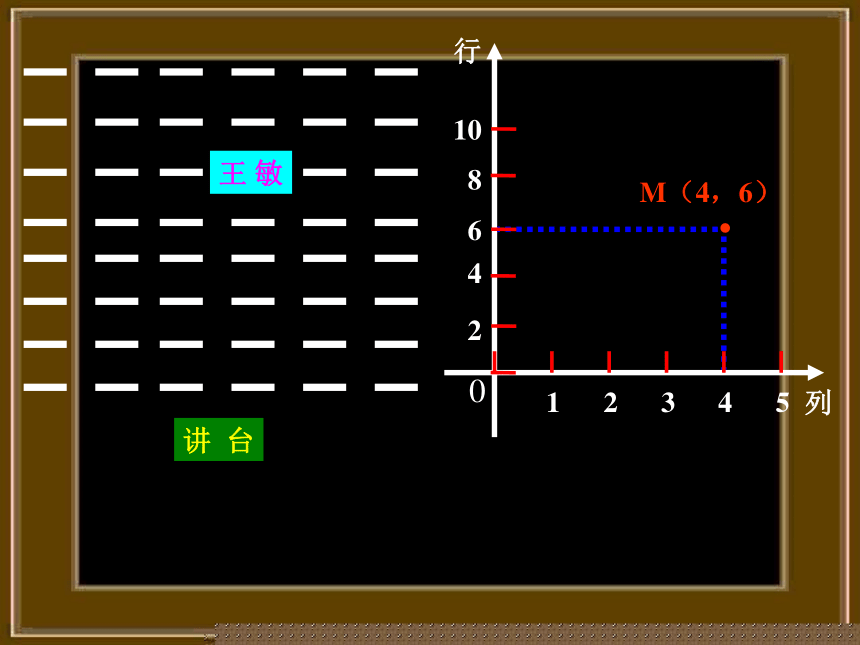
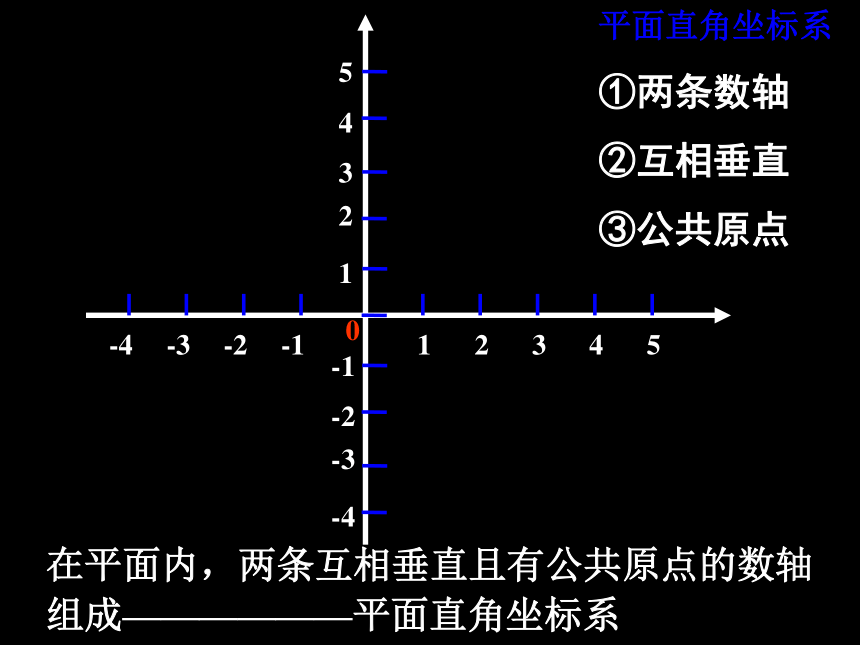
因为电影票上都标有“×排×座”的字样,所以找座位时,先找到第几排,再找到这一排的第几座就可以了.也就是说,电影院里的座位完全可以由两个数确定下来.问题2 在教室里,怎样确定一个同学的座位?例如,××同学在第3行第4排.这样教室里座位也可以用一对实数表示.讲 台王 敏·M(4,6)在数学中,我们可以用一对有序实数来确定平面上点的位置.为此,在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系.通常把其中水平的一条数轴叫做x轴或横轴,取向右为正方向;铅直的数轴叫做y轴或纵轴,取向上为正方向;两数轴的交点O叫做坐标原点.在平面内,两条互相垂直且有公共原点的数轴组成——————平面直角坐标系平面直角坐标系
①两条数轴
②互相垂直
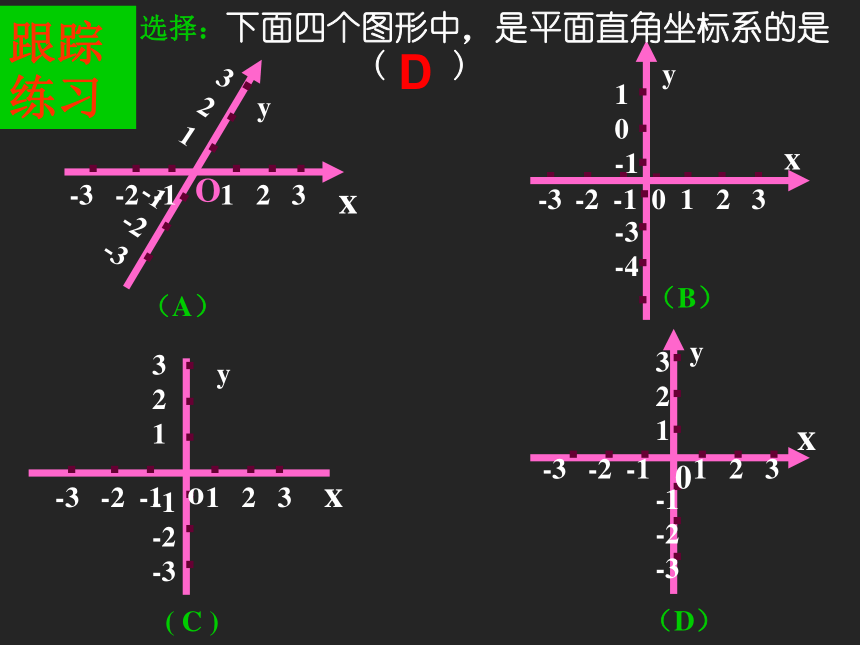
③公共原点 xO 选择:下面四个图形中,是平面直角坐标系的是
( )xxy(A)y(B) -3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y(D)0跟踪练习D -3 -2 -1 0 1 2 3 1
0
-1
-3
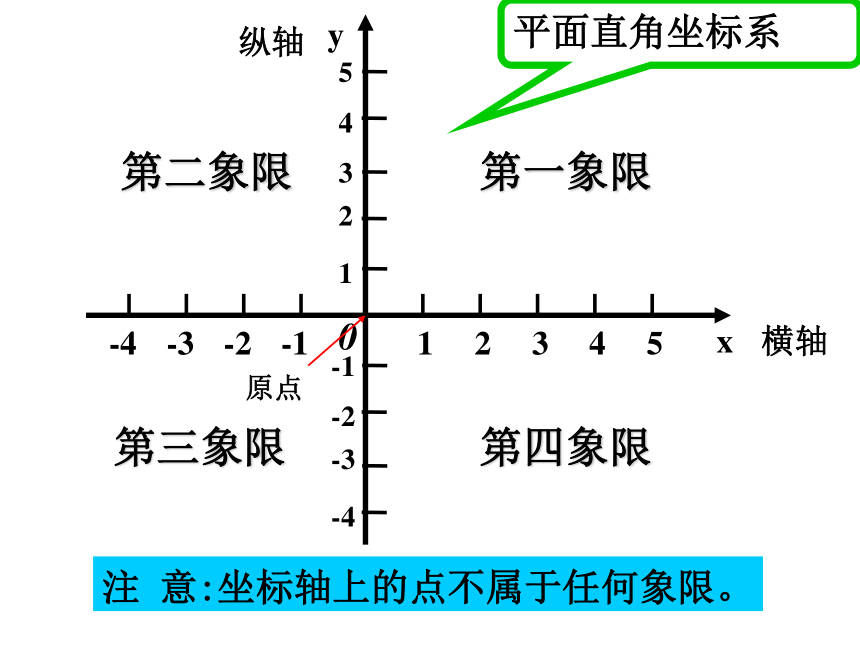
-4x0第一象限第四象限第三象限第二象限注 意:坐标轴上的点不属于任何象限。平面直角坐标系在平面直角坐标系中,任意一点都可以用一对有序实数来表示.例如,图中的点P,从点P分别向x轴和y轴作垂线,垂足分别为M和N.这时,点M在x轴上对应的数为3,称为点P的横坐标;点N在y轴上对应的数为2,称为点P的纵坐标.依次写出点P的横坐标和纵坐标,得到一对有序实数(3,2),称为点P的坐标.这时点P可记作P(3,2). ···A0A点的横坐标为3A点的纵坐标为2A点在平面直角坐标系中的坐标为(3, 2)
记作:A(3,2)B (-3, 1)A1A2( 2,4 )( 4,2 )( -2,1 )( -4,- 3 )( 1,- 2 )例1:写出图中A、B、C、D、E、F、G各点的坐标。(0,5 )(5,0 )思考:1、每个象限上点的坐标的符号各有什么特点?2、坐标轴上点的坐标有什么特点?(+, + )(- ,+)(- ,-)(+ , -)练习、写出图中A、B、C、D、E、F各点的坐标。横坐标是正数,
纵坐标是正数; 横坐标是负数,
纵坐标是正数;横坐标是负数,
纵坐标是负数;横坐标是正数,
纵坐标是负数;(+, + )(- ,+)(- ,-)(+ , -)练习、写出图中A、B、C、D、E、F各点的坐标。Y轴上点的
横坐标等于0X轴上点的
纵坐标等于0点在x轴上表示为(x,0) ,点在y轴上表示为(0,y)原点表示为(0,0)例2 在 右图中分别描出坐标是(2,3)、(-2,3)、(3,-2)的点Q、S、R,Q(2,3)与P(3,2)是同一点吗?S(-2,3)与R(3,-2)是同一点吗?解: Q(2,3)与P(3,2)不是同一点;
S(-2,3)与R(3,-2)不是同一点.·B0·A·E·D( 2,3 )( 3,2 )( -2,1 )( -4,- 3 )( 1,- 2 )练习、写出图中A、B、C、D、E各点的坐标。 从上面的例1、例2可以发现直角坐标系上每一个点的位置都能用一对有序实数表示,反之,任何一对有序实数在直角坐标系上都有唯一的一个点和它对应.也就是说直角坐标系上的点和有序实数对是一一对应的. 例3 在直角坐标系中描出点A(2,-3),分别找出它关于x轴、y轴及原点的对称点,并写出这些点的坐标.观察上述写出的各点的坐标,回答:
(1)关于x轴对称的两点的坐标之间有什么关系?
(2)关于?y轴对称的两点的坐标之间有什么关系?
(3)关于原点对称的两点的坐标之间有什么关系?解(1)关于x轴对称的两点:横坐标相同,纵坐标相反;(2)关于y轴对称的两点:横坐标相反,纵坐标相同;(3)关于原点对称的两点:横坐标相反,纵坐标相反.★若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )a,-b- a, b-a,-b例.点P(-2,3)关于x轴对称的点的对称点坐标是 .(-2,-3)练习:
1、判断正误(1)坐标平面内的一点,一定在第一象限、第二象
限、第三象限、第四象限这四个象限中的一个
象限内. ( )(2)在同一直角坐标系中,点 (5, 3)与点(3, 5)是相同的两点. ( )(3)原点O的坐标是 ( 0, 0 ) . ( )试一试练习:1、下列点位于第四象限的是( )A、(2,-3)B、(-2,-3)C、(2,3)D、(-2,3)2、若点A(x,y)的坐标满足xy=0,则点A在( )上A、原点B、x轴C、y轴D、x轴或y轴3、在平面直角坐标系内,下列说法错误的是( )A、原点O不在任何象限内B、原点O的坐标是0C、原点O既在x轴也在y 轴上D、原点O在直角坐标平面内ADB1.平面直角坐标系的有关概念及画法;2.在直角坐标系中,根据坐标找出点;由点求出坐标的方法;3.在四个象限内的点的坐标特征;两条坐标轴上的点的坐标特征;第一、三象限角平分线上点的坐标特征;第二、四象限角平分线上点的坐标特征;4.分别关于x轴、y轴及原点的对称的两点坐标之间的关系.这节课你学到了什么?一、根据A、B、C、D各点的坐标,你能发现各个象限内的点的坐标有什么特征吗?
探索与思考结论设M点的坐标为(x,y),则
若M在第一象限,则x>0,y>0
若M在第二象限,则x<0,y>0
若M在第三象限,则x<0,y<0
若M在第四象限,则x>0,y<0
检测反馈 1.判断下列说法是否正确:
(1)(2,3)和(3,2)表示同一点;
(2)点(-4,1)与点(4,-1)关于原点对称;
(3)坐标轴上的点的横坐标和纵坐标至少有一个为0;
(4)第一象限内的点的横坐标与纵坐标均为正数.2.指出下列各点所在的象限或坐标轴:
A(-3,-5),B(6,-7),C(0,-6),
D(-3,5),E(4,0).检测反馈 3.填空:
(1)点P(5,-3)关于x轴对称点的坐标是 ;
(2)点P(3,-5)关于y轴对称点的坐标是 ;
(3)点P(-2,-4)关于原点对称点的坐标是 . 再见作业:
完成练习册上的练习26页
-1, 2.5 , 0, 0.5问题1 你去过电影院吗?还记得在电影院是怎么找座位的吗?解
因为电影票上都标有“×排×座”的字样,所以找座位时,先找到第几排,再找到这一排的第几座就可以了.也就是说,电影院里的座位完全可以由两个数确定下来.问题2 在教室里,怎样确定一个同学的座位?例如,××同学在第3行第4排.这样教室里座位也可以用一对实数表示.讲 台王 敏·M(4,6)在数学中,我们可以用一对有序实数来确定平面上点的位置.为此,在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系.通常把其中水平的一条数轴叫做x轴或横轴,取向右为正方向;铅直的数轴叫做y轴或纵轴,取向上为正方向;两数轴的交点O叫做坐标原点.在平面内,两条互相垂直且有公共原点的数轴组成——————平面直角坐标系平面直角坐标系
①两条数轴
②互相垂直
③公共原点 xO 选择:下面四个图形中,是平面直角坐标系的是
( )xxy(A)y(B) -3 -2 -1 1 2 3
3
2
1
-1
-2
-3
y(D)0跟踪练习D -3 -2 -1 0 1 2 3 1
0
-1
-3
-4x0第一象限第四象限第三象限第二象限注 意:坐标轴上的点不属于任何象限。平面直角坐标系在平面直角坐标系中,任意一点都可以用一对有序实数来表示.例如,图中的点P,从点P分别向x轴和y轴作垂线,垂足分别为M和N.这时,点M在x轴上对应的数为3,称为点P的横坐标;点N在y轴上对应的数为2,称为点P的纵坐标.依次写出点P的横坐标和纵坐标,得到一对有序实数(3,2),称为点P的坐标.这时点P可记作P(3,2). ···A0A点的横坐标为3A点的纵坐标为2A点在平面直角坐标系中的坐标为(3, 2)
记作:A(3,2)B (-3, 1)A1A2( 2,4 )( 4,2 )( -2,1 )( -4,- 3 )( 1,- 2 )例1:写出图中A、B、C、D、E、F、G各点的坐标。(0,5 )(5,0 )思考:1、每个象限上点的坐标的符号各有什么特点?2、坐标轴上点的坐标有什么特点?(+, + )(- ,+)(- ,-)(+ , -)练习、写出图中A、B、C、D、E、F各点的坐标。横坐标是正数,
纵坐标是正数; 横坐标是负数,
纵坐标是正数;横坐标是负数,
纵坐标是负数;横坐标是正数,
纵坐标是负数;(+, + )(- ,+)(- ,-)(+ , -)练习、写出图中A、B、C、D、E、F各点的坐标。Y轴上点的
横坐标等于0X轴上点的
纵坐标等于0点在x轴上表示为(x,0) ,点在y轴上表示为(0,y)原点表示为(0,0)例2 在 右图中分别描出坐标是(2,3)、(-2,3)、(3,-2)的点Q、S、R,Q(2,3)与P(3,2)是同一点吗?S(-2,3)与R(3,-2)是同一点吗?解: Q(2,3)与P(3,2)不是同一点;
S(-2,3)与R(3,-2)不是同一点.·B0·A·E·D( 2,3 )( 3,2 )( -2,1 )( -4,- 3 )( 1,- 2 )练习、写出图中A、B、C、D、E各点的坐标。 从上面的例1、例2可以发现直角坐标系上每一个点的位置都能用一对有序实数表示,反之,任何一对有序实数在直角坐标系上都有唯一的一个点和它对应.也就是说直角坐标系上的点和有序实数对是一一对应的. 例3 在直角坐标系中描出点A(2,-3),分别找出它关于x轴、y轴及原点的对称点,并写出这些点的坐标.观察上述写出的各点的坐标,回答:
(1)关于x轴对称的两点的坐标之间有什么关系?
(2)关于?y轴对称的两点的坐标之间有什么关系?
(3)关于原点对称的两点的坐标之间有什么关系?解(1)关于x轴对称的两点:横坐标相同,纵坐标相反;(2)关于y轴对称的两点:横坐标相反,纵坐标相同;(3)关于原点对称的两点:横坐标相反,纵坐标相反.★若设点M(a,b),
M点关于X轴的对称点M1( )
M点关于Y轴的对称点M2( ),
M点关于原点O的对称点M3( )a,-b- a, b-a,-b例.点P(-2,3)关于x轴对称的点的对称点坐标是 .(-2,-3)练习:
1、判断正误(1)坐标平面内的一点,一定在第一象限、第二象
限、第三象限、第四象限这四个象限中的一个
象限内. ( )(2)在同一直角坐标系中,点 (5, 3)与点(3, 5)是相同的两点. ( )(3)原点O的坐标是 ( 0, 0 ) . ( )试一试练习:1、下列点位于第四象限的是( )A、(2,-3)B、(-2,-3)C、(2,3)D、(-2,3)2、若点A(x,y)的坐标满足xy=0,则点A在( )上A、原点B、x轴C、y轴D、x轴或y轴3、在平面直角坐标系内,下列说法错误的是( )A、原点O不在任何象限内B、原点O的坐标是0C、原点O既在x轴也在y 轴上D、原点O在直角坐标平面内ADB1.平面直角坐标系的有关概念及画法;2.在直角坐标系中,根据坐标找出点;由点求出坐标的方法;3.在四个象限内的点的坐标特征;两条坐标轴上的点的坐标特征;第一、三象限角平分线上点的坐标特征;第二、四象限角平分线上点的坐标特征;4.分别关于x轴、y轴及原点的对称的两点坐标之间的关系.这节课你学到了什么?一、根据A、B、C、D各点的坐标,你能发现各个象限内的点的坐标有什么特征吗?
探索与思考结论设M点的坐标为(x,y),则
若M在第一象限,则x>0,y>0
若M在第二象限,则x<0,y>0
若M在第三象限,则x<0,y<0
若M在第四象限,则x>0,y<0
检测反馈 1.判断下列说法是否正确:
(1)(2,3)和(3,2)表示同一点;
(2)点(-4,1)与点(4,-1)关于原点对称;
(3)坐标轴上的点的横坐标和纵坐标至少有一个为0;
(4)第一象限内的点的横坐标与纵坐标均为正数.2.指出下列各点所在的象限或坐标轴:
A(-3,-5),B(6,-7),C(0,-6),
D(-3,5),E(4,0).检测反馈 3.填空:
(1)点P(5,-3)关于x轴对称点的坐标是 ;
(2)点P(3,-5)关于y轴对称点的坐标是 ;
(3)点P(-2,-4)关于原点对称点的坐标是 . 再见作业:
完成练习册上的练习26页
