2022--2023学年人教版八年级数学下册 17.1 勾股定理 课后练习 (无答案)
文档属性
| 名称 | 2022--2023学年人教版八年级数学下册 17.1 勾股定理 课后练习 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 304.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 08:00:27 | ||
图片预览

文档简介
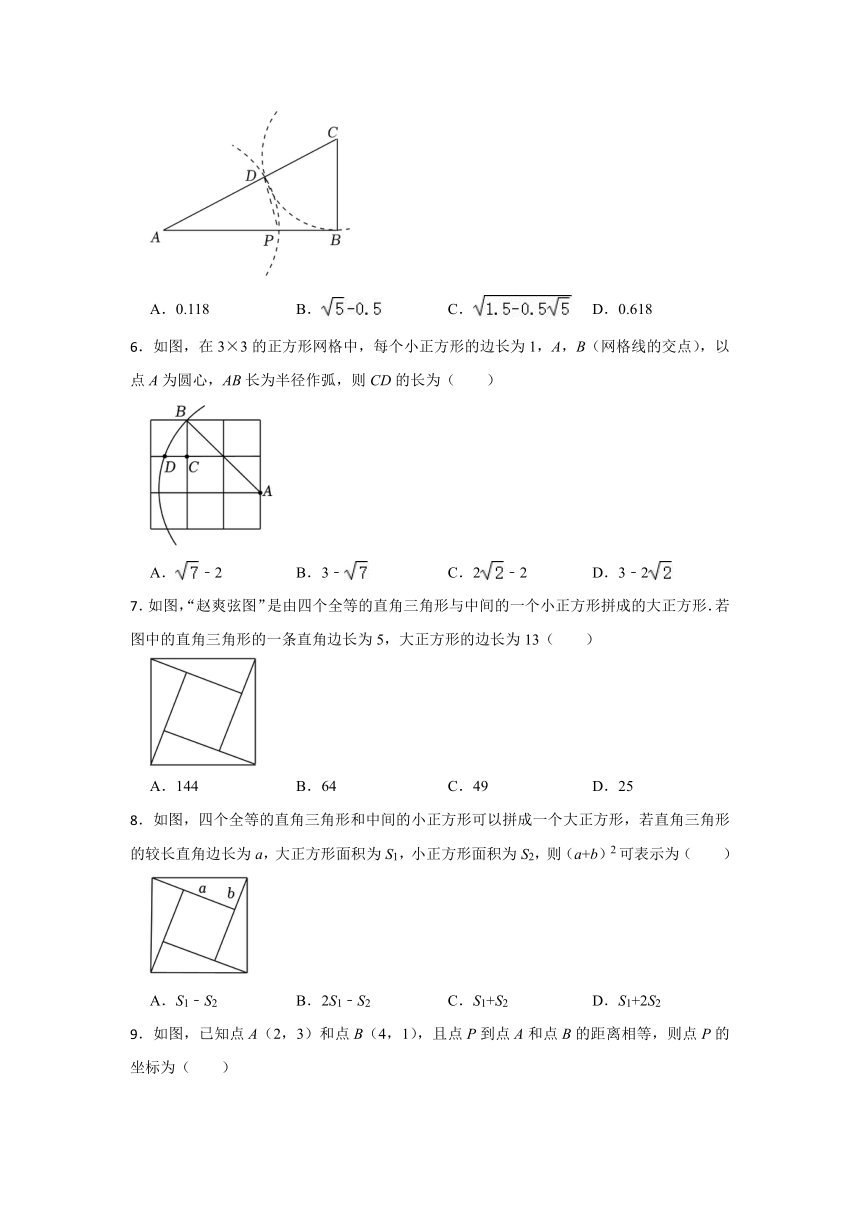
17.1 勾股定理(课后练习)-人教版八年级下册
一.选择题
1.现有两根木棒的长度分别为40cm和50cm.若要钉成一个直角三角形框架,那么所需要最短的木棒长是( )
A.50cm B.40cm C.30cm D.以上都不对
2.如图,△ABC中,AB=AC=,分别以点B,C为圆心、大于,两弧交于点E,作射线AE,连接DC.若CD=5,则AD的长为( )
A.10 B.11 C.12 D.6
3.如图,在△ABC中,∠C=90°,则AC2+BC2的值是( )
A.10 B.34 C.25 D.41
4.已知一个无盖长方体盒子的底面是边长为2的正方形,侧面是长为4的长方形.现展开铺平,如图,B,C,D得到一个正方形,将四个长方形沿虚线各剪去一个直角三角形( )
A. B. C. D.2
.如图,BC⊥AB,BC=,试求的小数部分( )
A.0.118 B. C. D.0.618
.如图,在3×3的正方形网格中,每个小正方形的边长为1,A,B(网格线的交点),以点A为圆心,AB长为半径作弧,则CD的长为( )
A.﹣2 B.3﹣ C.2﹣2 D.3﹣2
.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形.若图中的直角三角形的一条直角边长为5,大正方形的边长为13( )
A.144 B.64 C.49 D.25
.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,大正方形面积为S1,小正方形面积为S2,则(a+b)2可表示为( )
A.S1﹣S2 B.2S1﹣S2 C.S1+S2 D.S1+2S2
.如图,已知点A(2,3)和点B(4,1),且点P到点A和点B的距离相等,则点P的坐标为( )
A.(1,0) B.(0,﹣1)
C.(1,0)或(0,﹣1) D.(2,0)或(0,1)
.如图,在△ABC中,∠C=90°,且BD=2,DC=32﹣AD2的值为( )
A.4 B.9 C.16 D.25
二.填空题
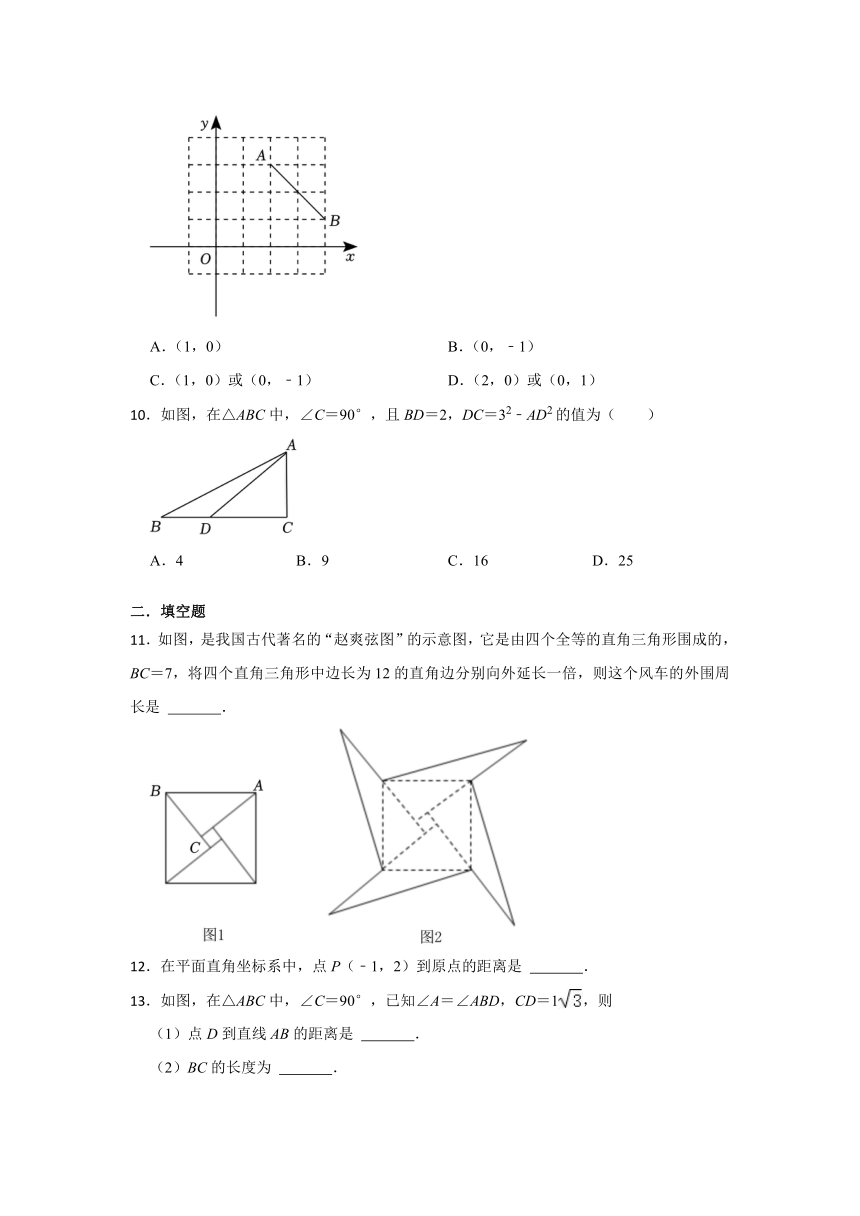
.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,则这个风车的外围周长是 .
.在平面直角坐标系中,点P(﹣1,2)到原点的距离是 .
.如图,在△ABC中,∠C=90°,已知∠A=∠ABD,CD=1,则
(1)点D到直线AB的距离是 .
(2)BC的长度为 .
.如图,Rt△ABC中,分别以这个三角形的三边为边长作正方形1、S2、S2.如果S2+S1﹣S3=18,则阴影部分的面积为 .
.已知,在△ABC中,AB=AC=10,B两题中任选一题作答.我选择题.
A.如图1,若BD⊥AC于点D,且DC=2 .
B.如图2,若BD=BC=2,则AD的长为 .
三.解答题
.如图,在△ABC中,AD⊥BC于D,BC=9,AD=4
.如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8(提示:=6.4)
.如图,方格纸上每个小正方形的边长都是1,线段AB的位置如图所示,B均为格点.
(1)请你在图中确定点C,并连接CA,CB,垂足为A,BC=5;
(2)在完成(1)后,请你在图中再确定点D,并连接DC,使DC=3,DB=
.如图1,将长为2a+3,宽为2a的矩形分割成四个全等的直角三角形(如图2),得到大小两个正方形.
(1)用关于a的代数式表示图2中小正方形的边长.
(2)当a=3时,该小正方形的面积是多少?
.图1是一个“有趣“的图形,它是由四个完全一样的直角三角形围成的一个大正方形ABCD,并且直角三角形的斜边又围成一个小正方形MNQP.已知每个直角三角形直角边分别是a,b(a<b)
(1)如图1,设中间的小正方形MNQP面积为S1,请用两种方法来表示S1.
(2)如图2,将四个三角形向里面翻折,刚好又能形成一个更小的正方形A'B'C′D'.已知正方形A'B'C′D'的边长为3,b的值.
(3)连结B'D',若B'D′∥AD,请问∠DMN是多少度?请说明理由.
一.选择题
1.现有两根木棒的长度分别为40cm和50cm.若要钉成一个直角三角形框架,那么所需要最短的木棒长是( )
A.50cm B.40cm C.30cm D.以上都不对
2.如图,△ABC中,AB=AC=,分别以点B,C为圆心、大于,两弧交于点E,作射线AE,连接DC.若CD=5,则AD的长为( )
A.10 B.11 C.12 D.6
3.如图,在△ABC中,∠C=90°,则AC2+BC2的值是( )
A.10 B.34 C.25 D.41
4.已知一个无盖长方体盒子的底面是边长为2的正方形,侧面是长为4的长方形.现展开铺平,如图,B,C,D得到一个正方形,将四个长方形沿虚线各剪去一个直角三角形( )
A. B. C. D.2
.如图,BC⊥AB,BC=,试求的小数部分( )
A.0.118 B. C. D.0.618
.如图,在3×3的正方形网格中,每个小正方形的边长为1,A,B(网格线的交点),以点A为圆心,AB长为半径作弧,则CD的长为( )
A.﹣2 B.3﹣ C.2﹣2 D.3﹣2
.如图,“赵爽弦图”是由四个全等的直角三角形与中间的一个小正方形拼成的大正方形.若图中的直角三角形的一条直角边长为5,大正方形的边长为13( )
A.144 B.64 C.49 D.25
.如图,四个全等的直角三角形和中间的小正方形可以拼成一个大正方形,若直角三角形的较长直角边长为a,大正方形面积为S1,小正方形面积为S2,则(a+b)2可表示为( )
A.S1﹣S2 B.2S1﹣S2 C.S1+S2 D.S1+2S2
.如图,已知点A(2,3)和点B(4,1),且点P到点A和点B的距离相等,则点P的坐标为( )
A.(1,0) B.(0,﹣1)
C.(1,0)或(0,﹣1) D.(2,0)或(0,1)
.如图,在△ABC中,∠C=90°,且BD=2,DC=32﹣AD2的值为( )
A.4 B.9 C.16 D.25
二.填空题
.如图,是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的,BC=7,将四个直角三角形中边长为12的直角边分别向外延长一倍,则这个风车的外围周长是 .
.在平面直角坐标系中,点P(﹣1,2)到原点的距离是 .
.如图,在△ABC中,∠C=90°,已知∠A=∠ABD,CD=1,则
(1)点D到直线AB的距离是 .
(2)BC的长度为 .
.如图,Rt△ABC中,分别以这个三角形的三边为边长作正方形1、S2、S2.如果S2+S1﹣S3=18,则阴影部分的面积为 .
.已知,在△ABC中,AB=AC=10,B两题中任选一题作答.我选择题.
A.如图1,若BD⊥AC于点D,且DC=2 .
B.如图2,若BD=BC=2,则AD的长为 .
三.解答题
.如图,在△ABC中,AD⊥BC于D,BC=9,AD=4
.如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8(提示:=6.4)
.如图,方格纸上每个小正方形的边长都是1,线段AB的位置如图所示,B均为格点.
(1)请你在图中确定点C,并连接CA,CB,垂足为A,BC=5;
(2)在完成(1)后,请你在图中再确定点D,并连接DC,使DC=3,DB=
.如图1,将长为2a+3,宽为2a的矩形分割成四个全等的直角三角形(如图2),得到大小两个正方形.
(1)用关于a的代数式表示图2中小正方形的边长.
(2)当a=3时,该小正方形的面积是多少?
.图1是一个“有趣“的图形,它是由四个完全一样的直角三角形围成的一个大正方形ABCD,并且直角三角形的斜边又围成一个小正方形MNQP.已知每个直角三角形直角边分别是a,b(a<b)
(1)如图1,设中间的小正方形MNQP面积为S1,请用两种方法来表示S1.
(2)如图2,将四个三角形向里面翻折,刚好又能形成一个更小的正方形A'B'C′D'.已知正方形A'B'C′D'的边长为3,b的值.
(3)连结B'D',若B'D′∥AD,请问∠DMN是多少度?请说明理由.
