2022-2023学年人教版九年级数学下册第二十七章 相似 单元练习题(含答案)
文档属性
| 名称 | 2022-2023学年人教版九年级数学下册第二十七章 相似 单元练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 255.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-16 08:05:57 | ||
图片预览

文档简介
第二十七章 相似
一、单项选择。
1.如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE∶BC的值为( )
A. B. C. D.
2.如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A,D为圆心,大于AD的长为半径画弧,两弧交于点M,N,作直线MN,分别交AC,AB于点E,F,则AE的长度为( )
A. B.3 C.2 D.
3.如图,AB∥CD∥EF.若=,BD=5,则DF的值为( )
A.5 B.10 C.15 D.20
4.如图,在△ABC中,DE∥BC,GF∥AC,下列式子错误的是( )
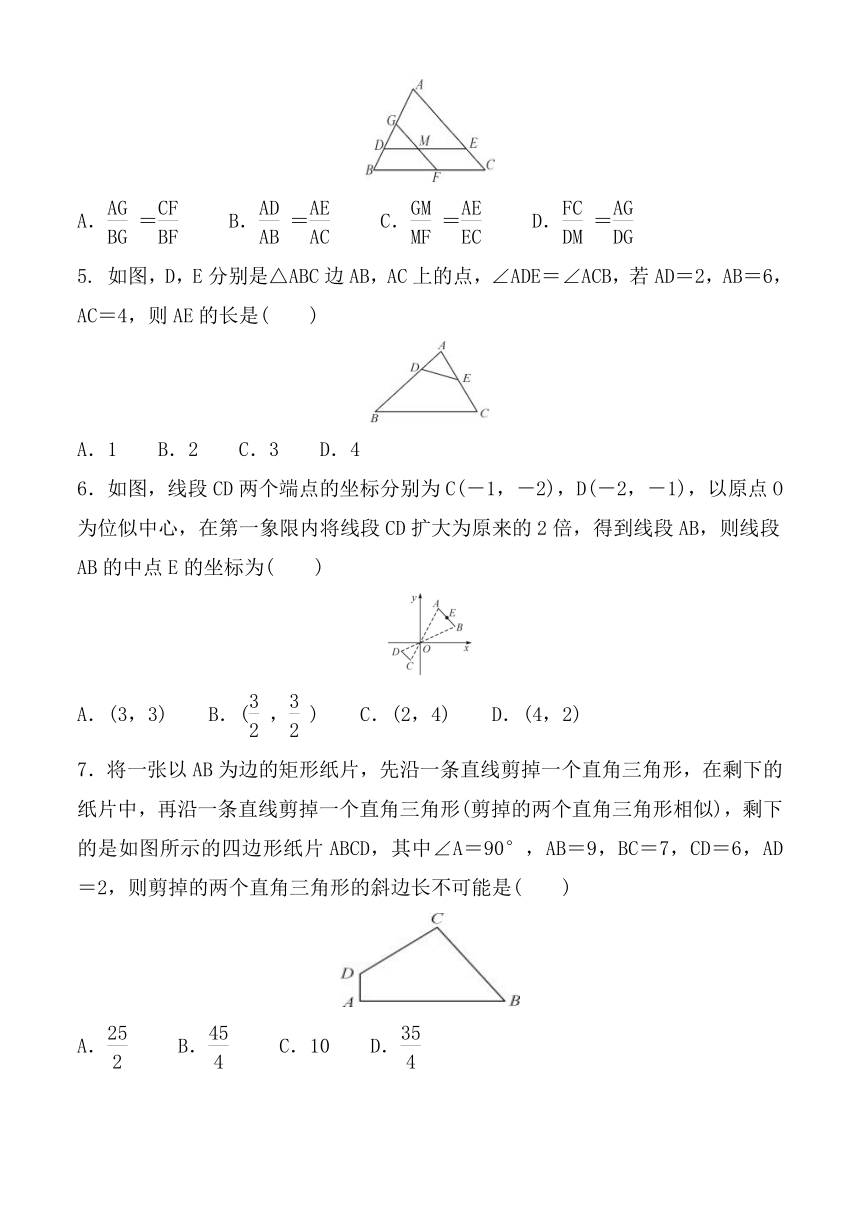
A.= B.= C.= D.=
5. 如图,D,E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
6.如图,线段CD两个端点的坐标分别为C(-1,-2),D(-2,-1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的2倍,得到线段AB,则线段AB的中点E的坐标为( )
A.(3,3) B.(,) C.(2,4) D.(4,2)
7.将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD,其中∠A=90°,AB=9,BC=7,CD=6,AD=2,则剪掉的两个直角三角形的斜边长不可能是( )
A. B. C.10 D.
二、填空题。
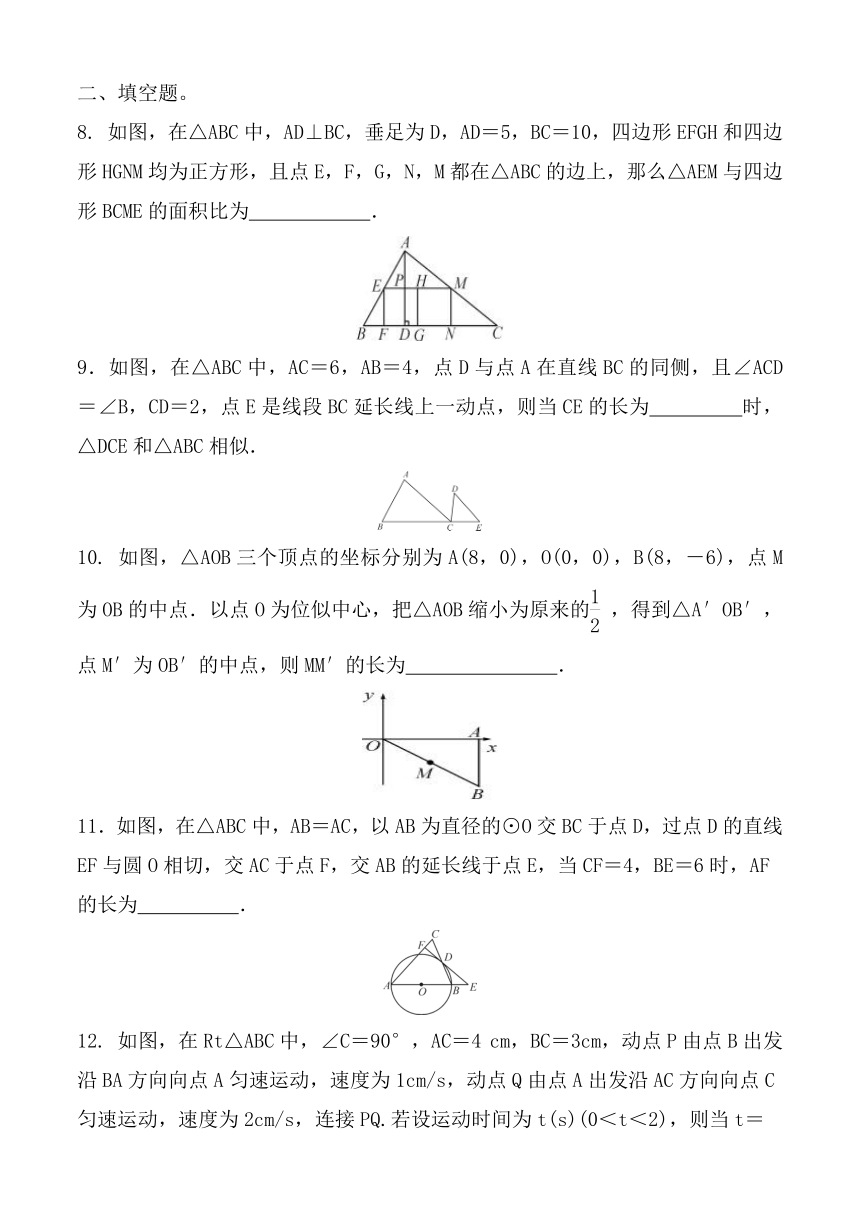
8. 如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E,F,G,N,M都在△ABC的边上,那么△AEM与四边形BCME的面积比为 .
9.如图,在△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠B,CD=2,点E是线段BC延长线上一动点,则当CE的长为 时,△DCE和△ABC相似.
10. 如图,△AOB三个顶点的坐标分别为A(8,0),O(0,0),B(8,-6),点M为OB的中点.以点O为位似中心,把△AOB缩小为原来的,得到△A′OB′,点M′为OB′的中点,则MM′的长为 .
11.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF与圆O相切,交AC于点F,交AB的延长线于点E,当CF=4,BE=6时,AF的长为 .
12. 如图,在Rt△ABC中,∠C=90°,AC=4 cm,BC=3cm,动点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s,动点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ.若设运动时间为t(s)(0<t<2),则当t=___________________s时,以A,P,Q为顶点的三角形与△ABC相似.
三、解答题。
13. 如图,在△ABC和△DEC中,∠A=∠D,∠BCE=∠ACD.
(1)求证:△ABC∽△DEC;
(2)若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.
14. 如图,在⊙O中,AB为⊙O的直径,直线DE与⊙O相切于点D,割线AC⊥DE于点E且交⊙O于点F,连接DF.求证:
(1)AD平分∠BAC;
(2)DF2=EF·AB.
15. 如图,在四边形ABCD中,AC与BD相交于点O,∠ABC=∠DAC=90°,BC=2AB,=,求的值.
16.如图,为测量水平地面上建筑物AB的高度,在点D和点F处分别竖立高是2m的标杆CD和EF,两标杆相隔52m,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2m到点G处,在G处测得建筑物顶端A,标杆顶端C在同一直线上;从标杆FE后退4m到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,求建筑物的高.
答案;
一、
1-7 AABCC AA
二、
8. 1∶3
9. 3或
10. 或
11. 20
12. 或
三、
解:(1)证明:∵∠BCE=∠ACD,∴∠BCE+∠ACE=∠ACD+∠ACE,
∴∠DCE=∠ACB,又∵∠A=∠D,∴△ABC∽△DEC
(2)∵△ABC∽△DEC,∴=()2=,又∵BC=6,∴CE=9
证明:(1)连接OD,如图所示,∵直线DE与⊙O相切于点D,AC⊥DE,
∴∠ODE=∠DEA=90°,∴OD∥AC,∴∠ODA=∠DAC.∵OA=OD,
∴∠OAD=∠ODA,∴∠DAC=∠OAD,∴AD平分∠BAC
连接OF,BD,如图所示,∵AC⊥DE,垂足为E,AB是⊙O的直径,
∴∠DEF=∠ADB=90°.∵∠EFD+∠AFD=180°,∠AFD+∠DBA=180°,∴∠EFD=∠DBA,∴△EFD∽△DBA,∴=,∴DB·DF=EF·AB,
由(1)知,AD平分∠BAC,∴∠FAD=∠DAB,∴DF=DB,∴DF2=EF·AB
15. 解:过点D作DM∥BC,交CA的延长线于点M,延长BA交DM于点N,图略.
∵DM∥BC,∴△ABC∽△ANM,△OBC∽△ODM,∴==,==,又∵∠ABC=∠DAC=90°,∴∠BAC+∠NAD=90°,∵∠BAC+∠BCA=90°,
∴∠NAD=∠BCA,∴△ABC∽△DNA,∴==,
设BC=6a,由==,得DM=5a,∴AB=3a,DN=a,AN=2a,
∴NB=AB+AN=3a+2a=5a,
∴===
16. 解:∵AB⊥BH,CD⊥BH,EF⊥BH,∴AB∥CD∥EF,∴△CDG∽△ABG,
△EFH∽△ABH.∴=,=,
∵CD=DG=EF=2m,DF=52m,FH=4m,∴=,=,
解得BD=52m,∴AB=54m,
即建筑物的高为54m
一、单项选择。
1.如图,在△ABC中,DE∥BC,DE分别与AB,AC相交于点D,E,若AD=4,DB=2,则DE∶BC的值为( )
A. B. C. D.
2.如图,在△ABC中,BC=6,AC=8,∠C=90°,以点B为圆心,BC长为半径画弧,与AB交于点D,再分别以A,D为圆心,大于AD的长为半径画弧,两弧交于点M,N,作直线MN,分别交AC,AB于点E,F,则AE的长度为( )
A. B.3 C.2 D.
3.如图,AB∥CD∥EF.若=,BD=5,则DF的值为( )
A.5 B.10 C.15 D.20
4.如图,在△ABC中,DE∥BC,GF∥AC,下列式子错误的是( )
A.= B.= C.= D.=
5. 如图,D,E分别是△ABC边AB,AC上的点,∠ADE=∠ACB,若AD=2,AB=6,AC=4,则AE的长是( )
A.1 B.2 C.3 D.4
6.如图,线段CD两个端点的坐标分别为C(-1,-2),D(-2,-1),以原点O为位似中心,在第一象限内将线段CD扩大为原来的2倍,得到线段AB,则线段AB的中点E的坐标为( )
A.(3,3) B.(,) C.(2,4) D.(4,2)
7.将一张以AB为边的矩形纸片,先沿一条直线剪掉一个直角三角形,在剩下的纸片中,再沿一条直线剪掉一个直角三角形(剪掉的两个直角三角形相似),剩下的是如图所示的四边形纸片ABCD,其中∠A=90°,AB=9,BC=7,CD=6,AD=2,则剪掉的两个直角三角形的斜边长不可能是( )
A. B. C.10 D.
二、填空题。
8. 如图,在△ABC中,AD⊥BC,垂足为D,AD=5,BC=10,四边形EFGH和四边形HGNM均为正方形,且点E,F,G,N,M都在△ABC的边上,那么△AEM与四边形BCME的面积比为 .
9.如图,在△ABC中,AC=6,AB=4,点D与点A在直线BC的同侧,且∠ACD=∠B,CD=2,点E是线段BC延长线上一动点,则当CE的长为 时,△DCE和△ABC相似.
10. 如图,△AOB三个顶点的坐标分别为A(8,0),O(0,0),B(8,-6),点M为OB的中点.以点O为位似中心,把△AOB缩小为原来的,得到△A′OB′,点M′为OB′的中点,则MM′的长为 .
11.如图,在△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,过点D的直线EF与圆O相切,交AC于点F,交AB的延长线于点E,当CF=4,BE=6时,AF的长为 .
12. 如图,在Rt△ABC中,∠C=90°,AC=4 cm,BC=3cm,动点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s,动点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s,连接PQ.若设运动时间为t(s)(0<t<2),则当t=___________________s时,以A,P,Q为顶点的三角形与△ABC相似.
三、解答题。
13. 如图,在△ABC和△DEC中,∠A=∠D,∠BCE=∠ACD.
(1)求证:△ABC∽△DEC;
(2)若S△ABC∶S△DEC=4∶9,BC=6,求EC的长.
14. 如图,在⊙O中,AB为⊙O的直径,直线DE与⊙O相切于点D,割线AC⊥DE于点E且交⊙O于点F,连接DF.求证:
(1)AD平分∠BAC;
(2)DF2=EF·AB.
15. 如图,在四边形ABCD中,AC与BD相交于点O,∠ABC=∠DAC=90°,BC=2AB,=,求的值.
16.如图,为测量水平地面上建筑物AB的高度,在点D和点F处分别竖立高是2m的标杆CD和EF,两标杆相隔52m,并且建筑物AB、标杆CD和EF在同一竖直平面内.从标杆CD后退2m到点G处,在G处测得建筑物顶端A,标杆顶端C在同一直线上;从标杆FE后退4m到点H处,在H处测得建筑物顶端A和标杆顶端E在同一直线上,求建筑物的高.
答案;
一、
1-7 AABCC AA
二、
8. 1∶3
9. 3或
10. 或
11. 20
12. 或
三、
解:(1)证明:∵∠BCE=∠ACD,∴∠BCE+∠ACE=∠ACD+∠ACE,
∴∠DCE=∠ACB,又∵∠A=∠D,∴△ABC∽△DEC
(2)∵△ABC∽△DEC,∴=()2=,又∵BC=6,∴CE=9
证明:(1)连接OD,如图所示,∵直线DE与⊙O相切于点D,AC⊥DE,
∴∠ODE=∠DEA=90°,∴OD∥AC,∴∠ODA=∠DAC.∵OA=OD,
∴∠OAD=∠ODA,∴∠DAC=∠OAD,∴AD平分∠BAC
连接OF,BD,如图所示,∵AC⊥DE,垂足为E,AB是⊙O的直径,
∴∠DEF=∠ADB=90°.∵∠EFD+∠AFD=180°,∠AFD+∠DBA=180°,∴∠EFD=∠DBA,∴△EFD∽△DBA,∴=,∴DB·DF=EF·AB,
由(1)知,AD平分∠BAC,∴∠FAD=∠DAB,∴DF=DB,∴DF2=EF·AB
15. 解:过点D作DM∥BC,交CA的延长线于点M,延长BA交DM于点N,图略.
∵DM∥BC,∴△ABC∽△ANM,△OBC∽△ODM,∴==,==,又∵∠ABC=∠DAC=90°,∴∠BAC+∠NAD=90°,∵∠BAC+∠BCA=90°,
∴∠NAD=∠BCA,∴△ABC∽△DNA,∴==,
设BC=6a,由==,得DM=5a,∴AB=3a,DN=a,AN=2a,
∴NB=AB+AN=3a+2a=5a,
∴===
16. 解:∵AB⊥BH,CD⊥BH,EF⊥BH,∴AB∥CD∥EF,∴△CDG∽△ABG,
△EFH∽△ABH.∴=,=,
∵CD=DG=EF=2m,DF=52m,FH=4m,∴=,=,
解得BD=52m,∴AB=54m,
即建筑物的高为54m
